10. NORMALIZATION
10.1.4: Transitive Functional Dependencies
Consider a relation that describes a couple of concepts, say instructor and department, and where the building shown is the building where the department is located, and the attribute instructor number is the only key:
|
instructor number |
instructor name |
office |
department code |
building |
|
33 |
Joe |
3D15 |
B&A |
Buhler |
|
44 |
Joe |
3D16 |
ACS |
Duckworth |
|
45 |
April |
3D17 |
ACS |
Duckworth |
|
50 |
Susan |
3D17 |
ACS |
Duckworth |
|
21 |
Peter |
3D18 |
B&A |
Buhler |
|
22 |
Peter |
3D18 |
MATH |
Duckworth |
As instructor number is the only key, we have the following FDs:
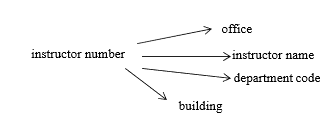
Suppose we also have the FD: department code determines building. Now our FD diagram becomes:

and we say the FD from instructor number to building is transitive via department code.
In general, if we have a relation with key A and functional dependencies:
A –> B and B –> C, then we say attribute A transitively determines attribute C.
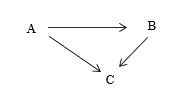
Note: B and C above are non-key attributes. If we also had the functional dependency B –> A (and so A and B are candidate keys) then A does not transitively determine C.
Exercises
1) Consider a relation that describes an employee including the province where the employee was born. Suppose the only key is employeeId and we have the attributes: name, birthDate, birthProvince, currentPopulation.
|
employeeId |
name |
birthDate |
birthProvince |
currentPopulation |
|
123 |
Joe |
Jan 1, 1990 |
MB |
1,200,000 |
|
222 |
Jennifer |
Jan 5, 1988 |
SK |
1,450,000 |
|
345 |
Jimmy |
Feb 5, 1987 |
MB |
1,200,000 |
|
… |
… |
… |
… |
… |
- What FDs would exist? Is there a transitive dependency?
2) Consider a relation with attributes X, Y, Z, W where the only CK is X, and the FDs are X –> Y, X –> Z, X –> W and Y –> Z. Is there a transitive dependency?

