1.10 Chapter 1 Example Solutions
1.2 Solutions
Example 1: Determining If Menu Price Lists Are Functions
- Let’s begin by considering the input as the items on the menu. The output values are then the prices. See Figure 1-11.

Figure 1-11 Each item on the menu has only one price, so the price is a function of the item.
- Two items on the menu have the same price. If we consider the prices to be the input values and the items to be the output, then the same input value could have more than one output associated with it. See Figure 1-12.
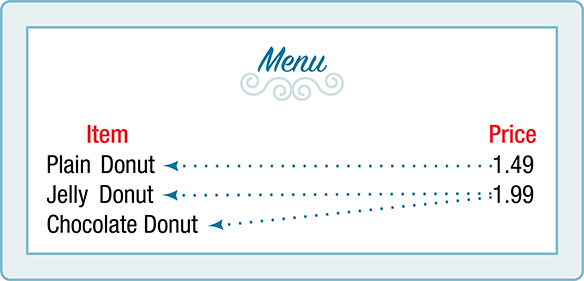
Figure 1-12 Therefore, the item is a not a function of price.
Example 2: Determining if Class Grade Rules are Functions
For any percent grade earned, there is an associated grade point average, so the grade point average is a function of the percent grade. In other words, if we input the percent grade, the output is a specific grade point average.
In the grading system given, there is a range of percent grades that correspond to the same grade point average. For example, students who receive a grade point average of 3.0 could have a variety of percent grades ranging from 78 all the way to 86. Thus, percent grade is not a function of grade point average.
Example 3: Determining if a Function is Present
- Yes.
- Yes. (Note: If two players had been tied for, say, 4th place, then the name would not have been a function of rank.)
1.3 Solutions
Example 1: Function Notation for Days in a Month
The number of days in a month is a function of the name of the month, so if we name the function [latex]f[/latex], we write [latex]\text{days}=f\left(\text{month}\right)[/latex] or [latex]d=f\left(m\right)[/latex]. The name of the month is the input to a “rule” that associates a specific number (the output) with each input.
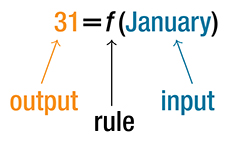
For example, [latex]\text{}f\left(\text{March}\right)=31\text{}[/latex], because March has 31 days. The notation [latex]\text{}d=f\left(m\right)\text{}[/latex] reminds us that the number of days, [latex]\text{}d\text{}[/latex] (the output), is dependent on the name of the month, [latex]\text{}m\text{}[/latex] (the input).
Example 2: Interpreting Function Notation
When we read [latex]\text{}f\left(2005\right)=300\text{}[/latex], we see that the input year is 2005. The value for the output, the number of police officers [latex]\text{}\left(N\right)\text{}[/latex], is 300. Remember, [latex]\text{}N=f\left(y\right)\text{}[/latex]. The statement [latex]\text{}f\left(2005\right)=300\text{}[/latex] tells us that in the year 2005 there were 300 police officers in the town.
Example 3: Using Function Notation
[latex]w=f\left(d\right)[/latex]
1.4 Solutions
Example 1: Identifying Tables that Represent Functions
Table 1-6 and Table 1-7 define functions. In both, each input value corresponds to exactly one output value. Table 1-8 does not define a function because the input value of 5 corresponds to two different output values.
When a table represents a function, corresponding input and output values can also be specified using function notation.
The function represented by Table 1-6 can be represented by writing
[latex]f\left(2\right)=1,f\left(5\right)=3,\text{and }f\left(8\right)=6[/latex]
Similarly, the statements
[latex]g\left(-3\right)=5,\text{}g\left(0\right)=1,\text{and }g\left(4\right)=5[/latex]
represent the function in Table 1-7.
Table 1-8 cannot be expressed in a similar way because it does not represent a function.
Example 2: Identifying Functions
Yes
1.5 Solutions
Exercise 1: Evaluating Functions at Specific Values
Replace the [latex]\text{}x\text{}[/latex] in the function with each specified value.
-
Because the input value is a number, 2, we can use simple algebra to simplify.
[latex]\begin{array}{l}\text{}\text{}f\left(2\right)={2}^{2}+3\left(2\right)-4\hfill \\ \text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}=4+6-4\hfill \\ \text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}=6\hfill \end{array}[/latex]
-
In this case, the input value is a letter so we cannot simplify the answer any further.
[latex]f\left(a\right)={a}^{2}+3a-4[/latex]
-
With an input value of [latex]\text{}a+h,\text{}[/latex] we must use the distributive property.
[latex]\begin{array}{l}f\left(a+h\right)={\left(a+h\right)}^{2}+3\left(a+h\right)-4\hfill \\ \text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}={a}^{2}+2ah+{h}^{2}+3a+3h-4\hfill \end{array}[/latex]
-
In this case, we apply the input values to the function more than once, and then perform algebraic operations on the result. We already found that
[latex]f\left(a+h\right)={a}^{2}+2ah+{h}^{2}+3a+3h-4[/latex]
and we know that
[latex]f\left(a\right)={a}^{2}+3a-4[/latex]
Now we combine the results and simplify.
[latex]\begin{array}{l}\begin{array}{l}\hfill \\ \frac{f\left(a+h\right)-f\left(a\right)}{h}=\frac{\left({a}^{2}+2ah+{h}^{2}+3a+3h-4\right)-\left({a}^{2}+3a-4\right)}{h}\hfill \end{array}\hfill \\ \begin{array}{ll}\text{ }=\frac{2ah+{h}^{2}+3h}{h}\hfill & \hfill \\ \text{ }=\frac{h\left(2a+h+3\right)}{h}\hfill & \begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}\text{Factor out }h.\hfill \\ \text{ }=2a+h+3\hfill & \begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}\text{Simplify}.\hfill \end{array}\hfill \end{array}[/latex]
Example 2: Evaluating Functions
-
To evaluate [latex]\text{}h\left(4\right),\text{}[/latex] we substitute the value 4 for the input variable [latex]\text{}p\text{}[/latex] in the given function.
[latex]\begin{array}{l}\text{ }h\left(p\right)={p}^{2}+2p\hfill \\ \text{ }h\left(4\right)={\left(4\right)}^{2}+2\left(4\right)\hfill \\ \text{ }=16+8\hfill \\ \text{ }=24\hfill \end{array}[/latex]
Therefore, for an input of 4, we have an output of 24.
- [latex]\text{}g\left(5\right)=1\text{}[/latex]
Example 3: Solving Functions
-
[latex]\begin{array}{llll}\text{ }h\left(p\right)=3\hfill & \hfill & \hfill & \hfill \\ \text{ }{p}^{2}+2p=3\hfill & \hfill & \hfill & \text{Substitute the original function }h\left(p\right)={p}^{2}+2p.\hfill \\ \text{ }{p}^{2}+2p-3=0\hfill & \hfill & \hfill & \text{Subtract 3 from each side}.\hfill \\ \text{ }\left(p+3\text{)(}p-1\right)=0\hfill & \hfill & \hfill & \text{Factor}.\hfill \end{array}[/latex]
If [latex]\text{}\left(p+3\right)\left(p-1\right)=0\text{}[/latex], either [latex]\text{}\left(p+3\right)=0\text{}[/latex] or [latex]\text{}\left(p-1\right)=0\text{}[/latex] (or both of them equal 0). We will set each factor equal to 0 and solve for [latex]\text{}p\text{}[/latex] in each case.
[latex]\begin{array}{ll}\left(p+3\right)=0,\hfill & p=-3\hfill \\ \left(p-1\right)=0,\hfill & p=1\hfill \end{array}[/latex]
This gives us two solutions. The output [latex]\text{}h\left(p\right)=3\text{}[/latex] when the input is either [latex]\text{}p=1\text{}[/latex] or [latex]\text{}p=-3\text{}[/latex]. We can also verify by graphing as in Figure 1-14. The graph verifies that [latex]\text{}h\left(1\right)=h\left(-3\right)=3\text{}[/latex] and [latex]\text{}h\left(4\right)=24[/latex].
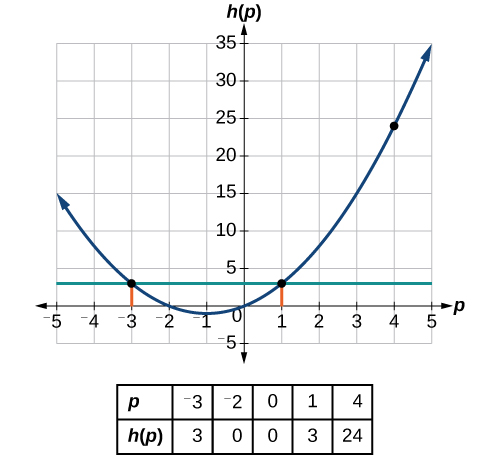
Figure 1-14 - [latex]\text{}m=8\text{}[/latex]
Example 4: Finding an Equation of a Function
To express the relationship in this form, we need to be able to write the relationship where [latex]\text{}p\text{}[/latex] is a function of [latex]\text{}n,\text{}[/latex] which means writing it as [latex]\text{}p=\left[\text{expression}\text{ }\text{involving}\text{ }n\right][/latex].
[latex]\begin{array}{ll}2n+6p=12\hfill & \hfill \\ \text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}6p=12-2n\hfill & \begin{array}{ccc}& & \end{array}\text{Subtract }2n\text{ from both sides}.\hfill \\ \text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}p=\frac{12-2n}{6}\hfill & \begin{array}{ccc}& & \end{array}\text{Divide both sides by 6 and simplify}.\hfill \\ \text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}p=\frac{12}{6}-\frac{2n}{6}\hfill & \hfill \\ \text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}p=2-\frac{1}{3}n\hfill & \hfill \end{array}[/latex]
Therefore, [latex]\text{}p\text{}[/latex] as a function of [latex]\text{}n\text{}[/latex] is written as
[latex]p=f\left(n\right)=2-\frac{1}{3}n[/latex]
Example 5: Expressing the Equation of a Circle as a Function
- First we subtract [latex]\text{}{x}^{2}\text{}[/latex] from both sides.
[latex]{y}^{2}=1-{x}^{2}[/latex]
We now try to solve for [latex]\text{}y\text{}[/latex] in this equation.
[latex]\begin{array}{l}y=±\sqrt{1-{x}^{2}}\hfill \\ \text{ }=+\sqrt{1-{x}^{2}}\text{ and }-\sqrt{1-{x}^{2}}\hfill \end{array}[/latex]
We get two outputs corresponding to the same input, so this relationship cannot be represented as a single function [latex]\text{}y=f\left(x\right)[/latex].
- [latex]y=f\left(x\right)=\frac{\sqrt[3]{x}}{2}[/latex]
Example 6: Evaluating and Solving a Tabular Function
- Evaluating [latex]g\left(3\right)[/latex] means determining the output value of the function [latex]g[/latex] for the input value of [latex]n=3[/latex]. The table output value corresponding to [latex]n=3[/latex] is 7, so [latex]g\left(3\right)=7[/latex].
- Solving [latex]g\left(n\right)=6[/latex] means identifying the input values, [latex]n[/latex], that produce an output value of 6. Table 1-15 shows two solutions: [latex]2[/latex] and [latex]4[/latex].
Table 1-15 [latex]n[/latex] 1 2 3 4 5 [latex]g\left(n\right)[/latex] 8 6 7 6 8 When we input 2 into the function [latex]\text{}g,\text{}[/latex] our output is 6. When we input 4 into the function [latex]\text{}g,\text{}[/latex] our output is also 6.
- [latex]g\left(1\right)=8[/latex]
Example 7: Reading Function Values from a Graph
- To evaluate [latex]\text{}f\left(2\right)\text{}[/latex], locate the point on the curve where [latex]\text{}x=2\text{}[/latex], then read the y-coordinate of that point. The point has coordinates [latex]\text{}\left(2,1\right)\text{}[/latex], so [latex]\text{}f\left(2\right)=1\text{}[/latex]. See Figure 1-15.
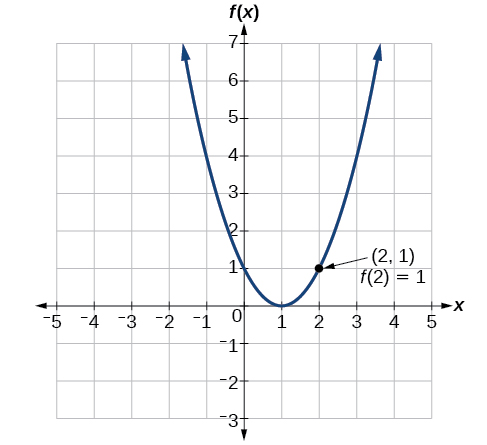
Figure 1-15 - To solve [latex]\text{}f\left(x\right)=4\text{}[/latex], we find the output value [latex]\text{}4\text{}[/latex] on the vertical axis. Moving horizontally along the line [latex]\text{}y=4\text{}[/latex], we locate two points of the curve with output value [latex]\text{}4:\left(-1,4\right)\text{}[/latex] and [latex]\text{}\left(3,4\right)\text{}[/latex]. These points represent the two solutions to [latex]\text{}f\left(x\right)=4:-1\text{}[/latex] or [latex]\text{}3\text{}[/latex]. This means [latex]\text{}f\left(-1\right)=4\text{}[/latex] and [latex]\text{}f\left(3\right)=4\text{}[/latex] or when the input is [latex]\text{}-1\text{}[/latex] or [latex]\text{3,}\text{}[/latex] the output is [latex]\text{}\text{4}\text{}\text{}[/latex]. See Figure 1-16.
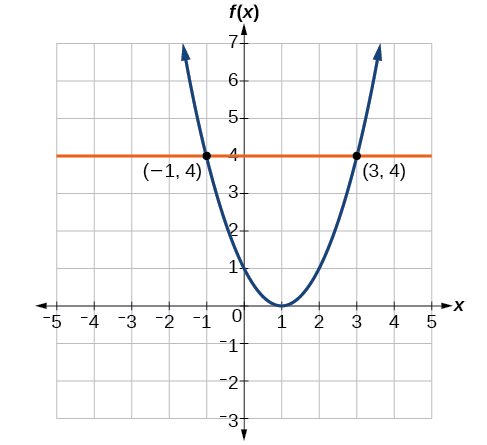
Figure 1-16 - [latex]x=0\text{}[/latex] or [latex]\text{}x=2\text{}[/latex]
1.6 Solutions
Example 1: Determining Whether a Relationship is a One-to-One Function
A circle of radius [latex]\text{}r\text{}[/latex] has a unique area measure given by [latex]\text{}A=\pi {r}^{2}[/latex], so for any input, [latex]\text{}r\text{}[/latex], there is only one output, [latex]A[/latex]. The area is a function of radius [latex]\text{}r[/latex].
If the function is one-to-one, the output value, the area, must correspond to a unique input value, the radius. Any area measure [latex]\text{}A\text{}[/latex] is given by the formula [latex]\text{}A=\pi {r}^{2}\text{}[/latex]. Because areas and radii are positive numbers, there is exactly one solution: [latex]\sqrt{\frac{A}{\pi }}[/latex]. So the area of a circle is a one-to-one function of the circle’s radius.
Example 2: Determining Whether a Relationship is a One-to-One Function
- Yes, because each bank account has a single balance at any given time;
- No, because several bank account numbers may have the same balance;
- No, because the same output may correspond to more than one input.
Example 3: Determining Whether a Relationship is a One-to-One Function
- Yes, letter grade is a function of percent grade;
- No, it is not one-to-one. There are 100 different percent numbers we could get but only about five possible letter grades, so there cannot be only one percent number that corresponds to each letter grade.
Example 4: Applying the Vertical Line Test
- If any vertical line intersects a graph more than once, the relation represented by the graph is not a function. Notice that any vertical line would pass through only one point of the two graphs shown in parts (a) and (b) of 1.6 Figure 1-8. From this we can conclude that these two graphs represent functions. The third graph does not represent a function because, at most x-values, a vertical line would intersect the graph at more than one point, as shown in Figure 1-17.
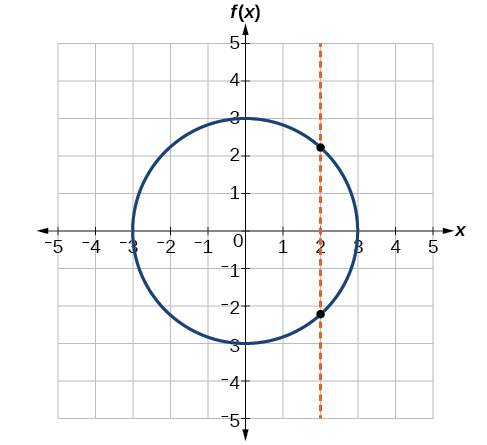
Figure 1-17 - Yes
Example 5: Applying the Horizontal Line Test
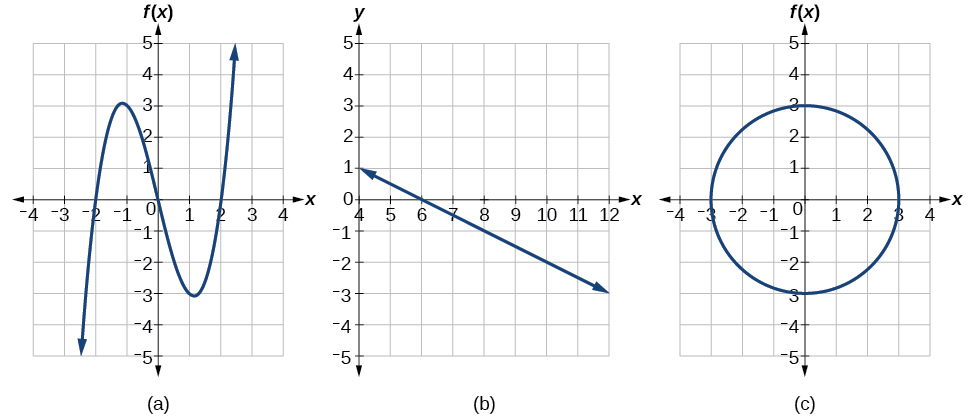
-
The function in Figure 1-18 (a) is not one-to-one. The horizontal line shown in Figure 1-19 intersects the graph of the function at two points (and we can even find horizontal lines that intersect it at three points.)
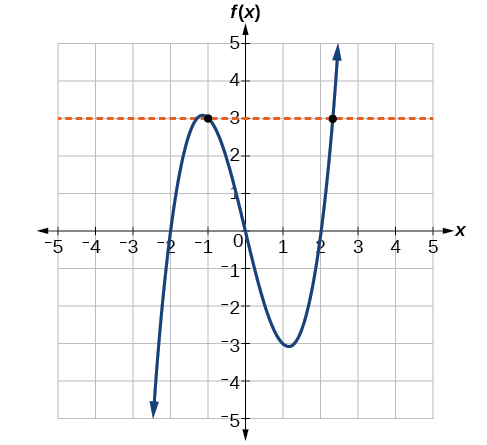
Figure 1-19 The function in Figure 1-18 (b) is one-to-one. Any horizontal line will intersect a diagonal line at most once.
- No, because it does not pass the horizontal line test.
Access for free at https://openstax.org/books/precalculus/pages/1-introduction-to-functions

