2.4 Finding Domain and Range from Graphs

Another way to identify the domain and range of functions is by using graphs. Because the domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the x-axis. The range is the set of possible output values, which are shown on the y-axis. Keep in mind that if the graph continues beyond the portion of the graph we can see, the domain and range may be greater than the visible values. See Figure 2-6.

Graph of a polynomial that shows the x-axis is the domain and the y-axis is the range
Figure 2-6

We can observe that the graph extends horizontally from [latex]\text{}-5\text{}[/latex] to the right without bound, so the domain is [latex]\text{}\left[-5,\infty \right)\text{}\text{}[/latex]. The vertical extent of the graph is all range values [latex]\text{}5\text{}[/latex] and below, so the range is [latex]\text{}\left(\mathrm{-\infty },5\right]\text{}[/latex]. Note that the domain and range are always written from smaller to larger values, or from left to right for domain, and from the bottom of the graph to the top of the graph for range.

Example 1: Finding Domain and Range from a Graph

Find the domain and range of the function [latex]\text{}f\text{}[/latex] whose graph is shown in Figure 2-7.

Graph of a function from (-3, 1].
Figure 2-7

Solution

Example 2: Finding the Domain and Range from a Graph

  1. Find the domain and range of the function [latex]\text{}f\text{}[/latex] whose graph is shown in Figure 2-8.[1]
    Graph of the Alaska Crude Oil Production where the y-axis is thousand barrels per day and the -axis is the years.
    Figure 2-8: (credit: modification of work by the U.S. Energy Information Administration)
  2. Given Figure 2-9, identify the domain and range using interval notation.
    Graph of World Population Increase where the y-axis represents millions of people and the x-axis represents the year.
    Figure 2-9

Solution

Question & Answer

Can a function’s domain and range be the same?

Yes. For example, the domain and range of the cube root function are both the set of all real numbers.

Access for free at https://openstax.org/books/precalculus/pages/1-introduction-to-functions

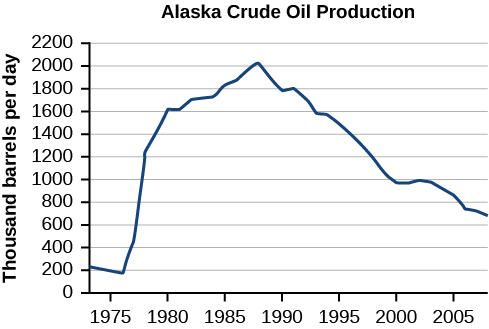
  1. http://www.eia.gov/dnav/pet/hist/LeafHandler.ashx?n=PET&s=MCRFPAK2&f=A. ↵

License

Icon for the Creative Commons Attribution 4.0 International License

Math 3080 Preparation Copyright © 2022 by Erin Kox is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book