1.2 Determining Whether a Relation Represents a Function
A relation is a set of ordered pairs. The set of the first components of each ordered pair is called the domain and the set of the second components of each ordered pair is called the range. Consider the following set of ordered pairs. The first numbers in each pair are the first five natural numbers. The second number in each pair is twice that of the first.
The domain is [latex]\left\{1,\text{}2,\text{}3,\text{}4,\text{}5\right\}[/latex]. The range is [latex]\left\{2,\text{}4,\text{}6,\text{}8,\text{}10\right\}[/latex].
Note that each value in the domain is also known as an input value, or independent variable, and is often labeled with the lowercase letter [latex]\text{}x\text{}[/latex]. Each value in the range is also known as an output value, or dependent variable, and is often labeled lowercase letter [latex]\text{}y\text{}[/latex].
A function, [latex]\text{}f\text{}[/latex], is a relation that assigns a single value in the range to each value in the domain. In other words, no x-values are repeated. For our example that relates the first five natural numbers to numbers double their values, this relation is a function because each element in the domain, [latex]\left\{1,\text{}2,\text{}3,\text{}4,\text{}5\right\}[/latex], is paired with exactly one element in the range, [latex]\left\{2,\text{}4,\text{}6,\text{}8,\text{}10\right\}[/latex].
Now let’s consider the set of ordered pairs that relates the terms “even” and “odd” to the first five natural numbers. It would appear as
Notice that each element in the domain, [latex]\left\{\text{even,}\text{}\text{odd}\right\}[/latex] is not paired with exactly one element in the range, [latex]\left\{1,\text{}2,\text{}3,\text{}4,\text{}5\right\}[/latex]. For example, the term “odd” corresponds to three values from the domain, [latex]\left\{1,\text{}3,\text{}5\right\}[/latex] and the term “even” corresponds to two values from the range, [latex]\left\{2,\text{}4\right\}[/latex]. This violates the definition of a function, so this relation is not a function.
Figure 1-2 compares relations that are functions and not functions.
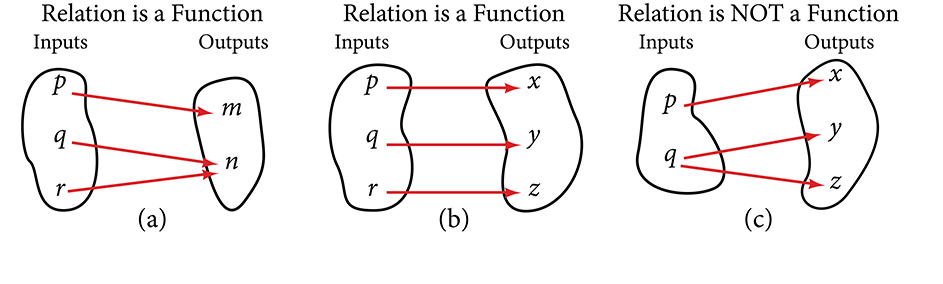
Function
A function is a relation in which each possible input value leads to exactly one output value. We say “the output is a function of the input.”
The input values make up the domain, and the output values make up the range.
How To
Given a relationship between two quantities, determine whether the relationship is a function.
- Identify the input values.
- Identify the output values.
- If each input value leads to only one output value, classify the relationship as a function. If any input value leads to two or more outputs, do not classify the relationship as a function.
Example 1: Determining if Menu Price Lists are Functions
The coffee shop menu, shown in Figure 1-3 consists of items and their prices.
- Is price a function of the item?
- Is the item a function of the price?
Example 2: Determining if Class Grade Rules are Functions
In a particular math class, the overall percent grade corresponds to a grade point average. Is grade point average a function of the percent grade? Is the percent grade a function of the grade point average? Table 1-1 shows a possible rule for assigning grade points.
| Percent grade | 0–56 | 57–61 | 62–66 | 67–71 | 72–77 | 78–86 | 87–91 | 92–100 |
|---|---|---|---|---|---|---|---|---|
| Grade point average | 0.0 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Example 3: Determining if a Function is Present
Table 1-2 lists the five greatest baseball players of all time in order of rank.
| Player | Rank |
|---|---|
| Babe Ruth | 1 |
| Willie Mays | 2 |
| Ty Cobb | 3 |
| Walter Johnson | 4 |
| Hank Aaron | 5 |
- Is the rank a function of the player name?
- Is the player name a function of the rank?
Access for free at https://openstax.org/books/precalculus/pages/1-introduction-to-functions
