3.4 Determining Even and Odd Functions
Some functions exhibit symmetry so that reflections result in the original graph. For example, horizontally reflecting the toolkit functions [latex]f\left(x\right)={x}^{2}[/latex] or [latex]f\left(x\right)=|x|[/latex] will result in the original graph. We say that these types of graphs are symmetric about the y-axis. Functions whose graphs are symmetric about the y-axis are called even functions.
If the graphs of[latex]\text{}f\left(x\right)={x}^{3}\text{}[/latex]or[latex]\text{}f\left(x\right)=\frac{1}{x}\text{}[/latex] were reflected over both axes, the result would be the original graph, as shown in Figure 3-11.
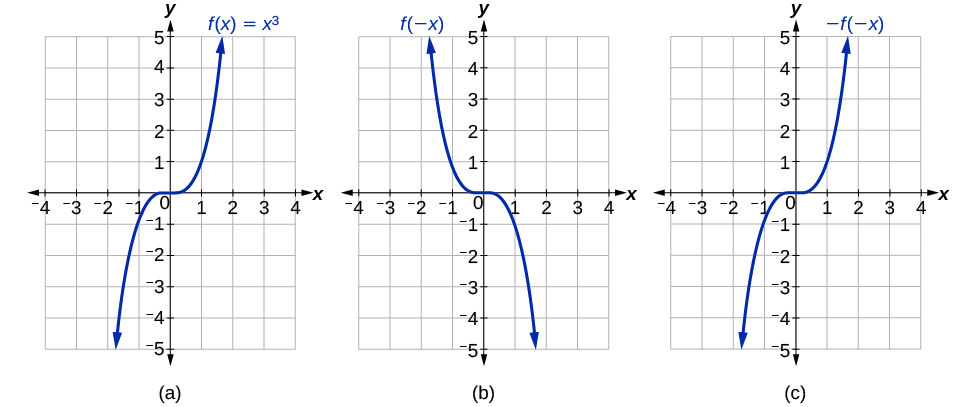
We say that these graphs are symmetric about the origin. A function with a graph that is symmetric about the origin is called an odd function.
Note: A function can be neither even nor odd if it does not exhibit either symmetry. For example, [latex]\text{}f\left(x\right)={2}^{x}\text{}[/latex] is neither even nor odd. Also, the only function that is both even and odd is the constant function [latex]\text{}f\left(x\right)=0[/latex].
Even and Odd Functions
A function is called an even function if for every input [latex]\text{}x[/latex]
[latex]f\left(x\right)=f\left(-x\right)[/latex]
The graph of an even function is symmetric about the [latex]y\text{-}[/latex] axis.
A function is called an odd function if for every input [latex]\text{}x[/latex]
[latex]f\left(x\right)=-f\left(-x\right)[/latex]
The graph of an odd function is symmetric about the origin.
How To
Given the formula for a function, determine if the function is even, odd, or neither.
- Determine whether the function satisfies [latex]\text{}f\left(x\right)=f\left(-x\right)\text{}[/latex]. If it does, it is even.
- Determine whether the function satisfies [latex]\text{}f\left(x\right)=-f\left(-x\right)\text{}[/latex]. If it does, it is odd.
- If the function does not satisfy either rule, it is neither even nor odd.
Example 1: Determining whether a Function is Even, Odd, or Neither
1. Is the function [latex]\text{}f\left(x\right)={x}^{3}+2x\text{}[/latex] even, odd, or neither?
Analysis
Consider the graph of [latex]\text{}f\text{}[/latex] in Figure 3-12. Notice that the graph is symmetric about the origin. For every point [latex]\text{}\left(x,y\right)\text{}[/latex] on the graph, the corresponding point [latex]\text{}\left(-x,-y\right)\text{}[/latex] is also on the graph. For example, (1, 3) is on the graph of [latex]\text{}f\text{}[/latex], and the corresponding point [latex]\left(-1,-3\right)[/latex] is also on the graph.
2. Is the function [latex]\text{}f\left(s\right)={s}^{4}+3{s}^{2}+7\text{}[/latex] even, odd, or neither?
Access for free at https://openstax.org/books/precalculus/pages/1-introduction-to-functions

