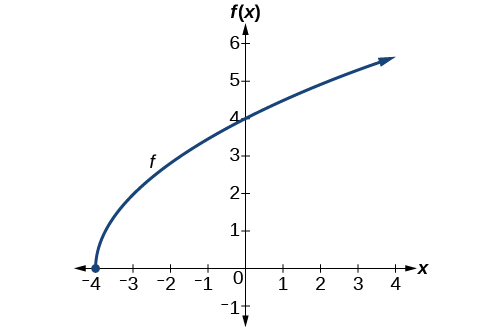
2.5 Finding Domains and Ranges of the Toolkit Functions

We will now return to our set of toolkit functions to determine the domain and range of each.

 

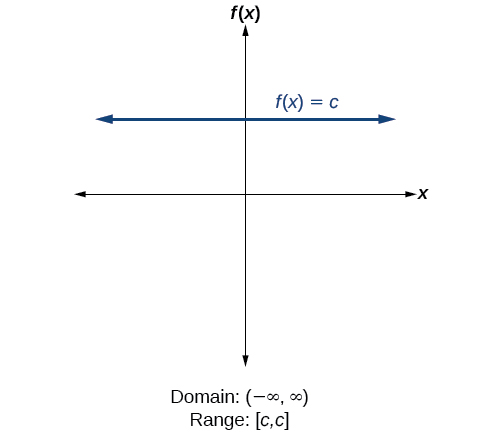
Constant function f(x)=c.
Figure 2-10: For the constant function [latex]\text{}f\left(x\right)=c,\text{}[/latex] the domain consists of all real numbers; there are no restrictions on the input. The only output value is the constant [latex]\text{}c,\text{}[/latex] so the range is the set [latex]\text{}\left\{c\right\}\text{}[/latex] that contains this single element. In interval notation, this is written as [latex]\text{}\left[c,c\right],\text{}[/latex] the interval that both begins and ends with [latex]\text{}c[/latex].
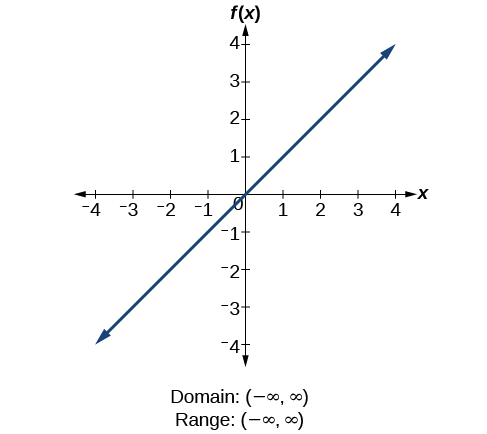
Identity function f(x)=x.
Figure 2-11: For the identity function [latex]\text{}f\left(x\right)=x,\text{}[/latex] there is no restriction on [latex]\text{}x\text{}[/latex]. Both the domain and range are the set of all real numbers.
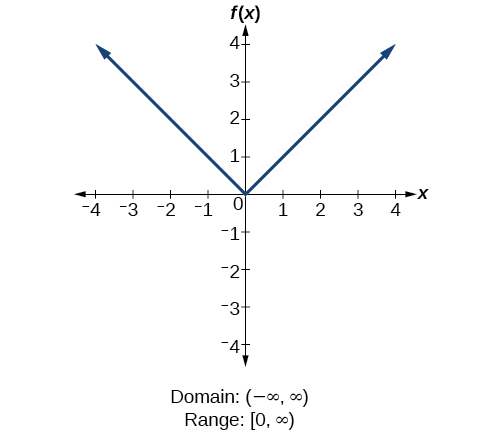
Absolute function f(x)=|x|.
Figure 2-12: For the absolute value function [latex]\text{}f\left(x\right)=|x|,\text{}[/latex]there is no restriction on [latex]\text{}x\text{}[/latex]. However, because absolute value is defined as a distance from 0, the output can only be greater than or equal to 0.
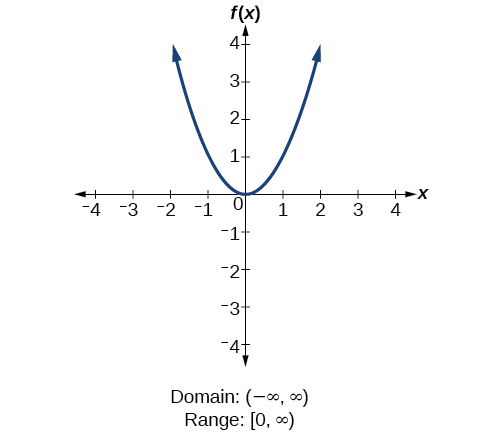
Quadratic function f(x)=x^2.
Figure 2-13: For the quadratic function [latex]\text{}f\left(x\right)={x}^{2},\text{}[/latex] the domain is all real numbers since the horizontal extent of the graph is the whole real number line. Because the graph does not include any negative values for the range, the range is only nonnegative real numbers.
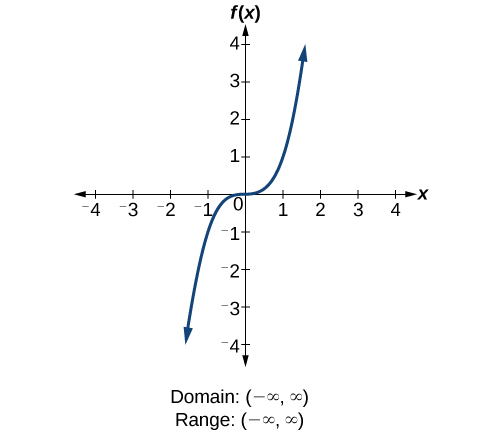
Cubic function f(x)-x^3.
Figure 2-14: For the cubic function [latex]\text{}f\left(x\right)={x}^{3}\text{}[/latex], the domain is all real numbers because the horizontal extent of the graph is the whole real number line. The same applies to the vertical extent of the graph, so the domain and range include all real numbers.
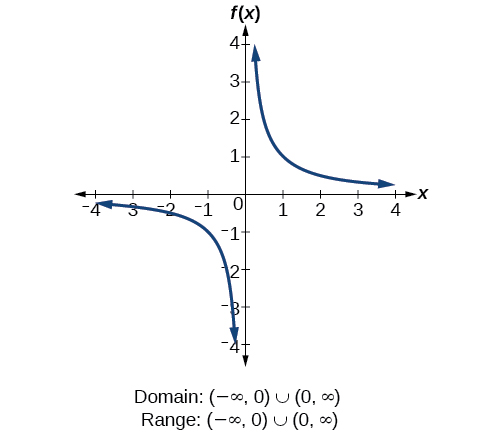
Reciprocal function f(x)=1/x.
Figure 2-15: For the reciprocal function [latex]\text{}f\left(x\right)=\frac{1}{x}\text{}[/latex], we cannot divide by 0, so we must exclude 0 from the domain. Further, 1 divided by any value can never be 0, so the range also will not include 0. In set-builder notation, we could also write [latex]\left\{x|\text{ }x\ne 0\right\}[/latex], the set of all real numbers that are not zero.
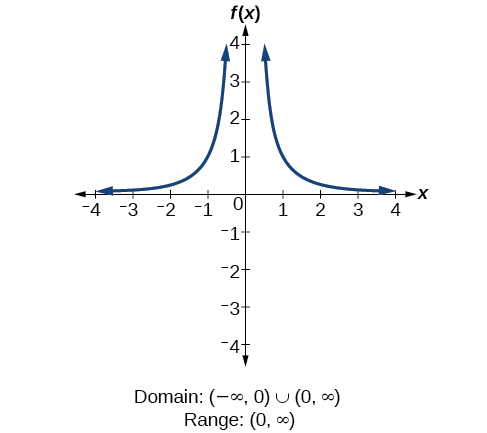
Reciprocal squared function f(x)=1/x^2
Figure 2-16: For the reciprocal squared function [latex]\text{}f\left(x\right)=\frac{1}{{x}^{2}}[/latex], we cannot divide by [latex]0[/latex], so we must exclude [latex]0[/latex] from the domain. There is also no [latex]x[/latex] that can give an output of 0, so 0 is excluded from the range as well. Note that the output of this function is always positive due to the square in the denominator, so the range includes only positive numbers.
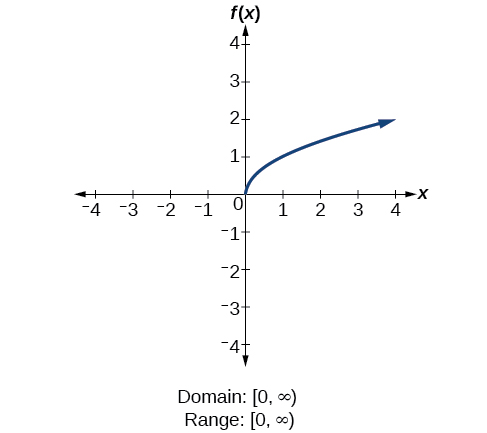
Square root function f(x)=sqrt(x).
Figure 2-17: For the square root function [latex]\text{}f\left(x\right)=\sqrt[]{x}\text{}[/latex], we cannot take the square root of a negative real number, so the domain must be 0 or greater. The range also excludes negative numbers because the square root of a positive number [latex]\text{}x\text{}[/latex] is defined to be positive, even though the square of the negative number [latex]\text{}-\sqrt{x}\text{}[/latex] also gives us [latex]\text{}x[/latex].
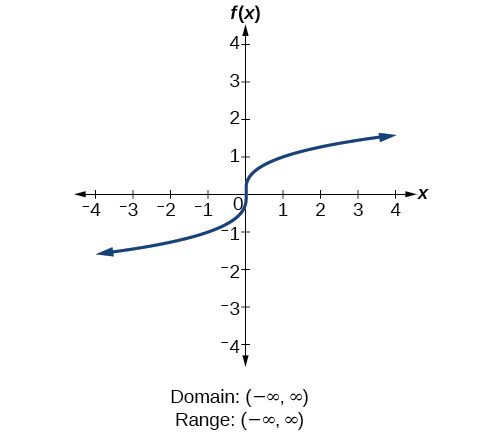
Cube root function f(x)=x^(1/3).
Figure 2-18: For the cube root function [latex]\text{}f\left(x\right)=\sqrt[3]{x}\text{}[/latex], the domain and range include all real numbers. Note that there is no problem taking a cube root, or any odd-integer root, of a negative number, and the resulting output is negative (it is an odd function).

How To

Given the formula for a function, determine the domain and range.

  1. Exclude from the domain any input values that result in division by zero.
  2. Exclude from the domain any input values that have non-real (or undefined) number outputs.
  3. Use the valid input values to determine the range of the output values.
  4. Look at the function graph and table values to confirm the actual function behaviour.

Example 1: Finding the Domain and Range Using Toolkit Functions

Find the domain and range of [latex]\text{}f\left(x\right)=2{x}^{3}-x[/latex].

Solution

Example 2: Finding Domain and Range

Find the domain and range of [latex]\text{}f\left(x\right)=\frac{2}{x+1}[/latex].

Solution

Example 3: Finding the Domain and Range

Find the domain and range of [latex]\text{}f\left(x\right)=2\sqrt{x+4}[/latex].

Analysis

Figure 2-19 represents the function [latex]\text{}f[/latex].

Graph of a square root function at (-4, 0).
Figure 2-19

Solution

Example 4: Finding the Domain and Range

Find the domain and range of [latex]\text{}f\left(x\right)=-\sqrt{2-x}[/latex].

Solution

Access for free at https://openstax.org/books/precalculus/pages/1-introduction-to-functions

License

Icon for the Creative Commons Attribution 4.0 International License

Math 3080 Preparation Copyright © 2022 by Erin Kox is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book