2.3 Using Notations to Specify Domain and Range
In the previous examples, we used inequalities and lists to describe the domain of functions. We can also use inequalities, or other statements that might define sets of values or data, to describe the behavior of the variable in set-builder notation. For example, [latex]\{x\vert10\leq x<30\}[/latex] describes the behavior of [latex]x[/latex] in set-builder notation. The braces [latex]\{\}[/latex] are read as “the set of,” and the vertical bar [latex]\vert[/latex] is read as “such that,” so we would read [latex]\{x\vert10\leq x<30\}[/latex] as “the set of x-values such that 10 is less than or equal to [latex]x\;[/latex] and [latex]\;x[/latex] is less than 30.”
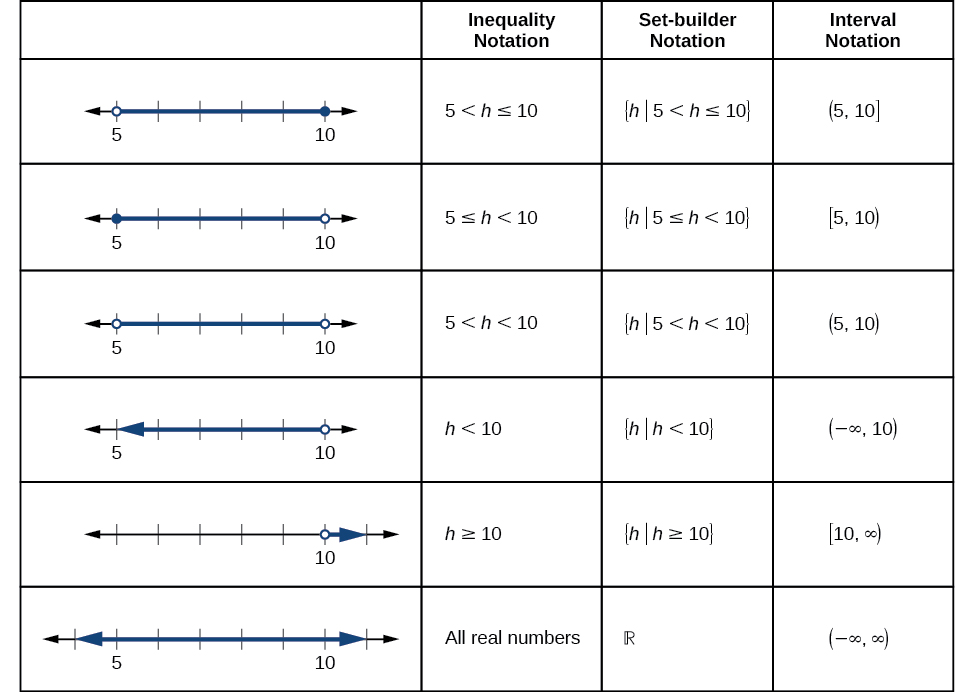
Figure 2-4 compares inequality notation, set-builder notation, and interval notation.
To combine two intervals using inequality notation or set-builder notation, we use the word “or.” As we saw in earlier examples, we use the union symbol, [latex]\cup[/latex] to combine two unconnected intervals. For example, the union of the sets [latex]\{2,3,5\}[/latex] and [latex]\{4,6\}[/latex] is the set [latex]\{2,3,4,5,6\}[/latex]. It is the set of all elements that belong to one or the other (or both) of the original two sets. For sets with a finite number of elements like these, the elements do not have to be listed in ascending order of numerical value. If the original two sets have some elements in common, those elements should be listed only once in the union set. For sets of real numbers on intervals, another example of a union is
Set-Builder Notation and Interval Notation
Set-builder notation is a method of specifying a set of elements that satisfy a certain condition. It takes the form [latex]\{x\vert\;statement\;about\;x\}[/latex] which is read as, “the set of all [latex]x[/latex] such that the statement about [latex]x[/latex] is true.” For example,
Interval notation is a way of describing sets that include all real numbers between a lower limit that may or may not be included and an upper limit that may or may not be included. The endpoint values are listed between brackets or parentheses. A square bracket indicates inclusion in the set, and a parenthesis indicates exclusion from the set. For example,
How To
Given a line graph, describe the set of values using interval notation.
- Identify the intervals to be included in the set by determining where the heavy line overlays the real line.
- At the left end of each interval, use [ with each end value to be included in the set ([latex]\bullet[/latex]) or ( for each excluded end value ([latex]\circ[/latex]).
- At the right end of each interval, use ] with each end value to be included in the set ([latex]\bullet[/latex]) or ) for each excluded end value ([latex]\circ[/latex]).
- Use the union symbol, ∪, to combine all intervals into one set.
Example 1: Describing Sets on the Real-Number Line
-
Describe the intervals of values shown in Figure 2-4 using inequality notation, set-builder notation, and interval notation.
Figure 2-4 -
Given Figure 2-5, specify the graphed set in
- words
- set-builder notation
- interval notation
Figure 2-5
Access for free at https://openstax.org/books/precalculus/pages/1-introduction-to-functions
