1.5 Finding Input and Output Values of a Function
When we know an input value and want to determine the corresponding output value for a function, we evaluate the function. Evaluating will always produce one result because each input value of a function corresponds to exactly one output value.
When we know an output value and want to determine the input values that would produce that output value, we set the output equal to the function’s formula and solve for the input. Solving can produce more than one solution because different input values can produce the same output value.
Evaluation of Functions in Algebraic Forms
When we have a function in formula form, it is usually a simple matter to evaluate the function. For example, the function [latex]\text{}f\left(x\right)=5-3{x}^{2}\text{}[/latex] can be evaluated by squaring the input value, multiplying by 3, and then subtracting the product from 5.
How To
Given the formula for a function, evaluate.
- Replace the input variable in the formula with the value provided.
- Calculate the result.
Example 1: Evaluating Functions at Specific Values
Evaluating Functions at Specific Values
Evaluate [latex]\text{}f\left(x\right)={x}^{2}+3x-4\text{}[/latex] at
- [latex]2[/latex]
- [latex]a[/latex]
- [latex]a+h[/latex]
- [latex]\frac{f\left(a+h\right)-f\left(a\right)}{h}[/latex]
Example 2: Evaluating Functions
- Given the function [latex]\text{}h\left(p\right)={p}^{2}+2p\text{}[/latex], evaluate [latex]\text{}h\left(4\right)\text{}[/latex].
- Given the function [latex]\text{}g\left(m\right)=\sqrt{m-4}\text{}[/latex], evaluate [latex]\text{}g\left(5\right)[/latex].
Example 3: Solving Functions
- Given the function [latex]\text{}h\left(p\right)={p}^{2}+2p\text{}[/latex] solve for [latex]\text{}h\left(p\right)=3[/latex].
- Given the function [latex]\text{}g\left(m\right)=\sqrt{m-4},\text{}[/latex] solve [latex]\text{}g\left(m\right)=2[/latex].
Evaluating Functions Expressed in Formulas
Some functions are defined by mathematical rules or procedures expressed in equation form. If it is possible to express the function output with a formula involving the input quantity, then we can define a function in algebraic form. For example, the equation [latex]\text{}2n+6p=12\text{}[/latex] expresses a functional relationship between [latex]\text{}n\text{}[/latex] and [latex]\text{}p\text{}[/latex]. We can rewrite it to decide if [latex]\text{}p\text{}[/latex] is a function of [latex]\text{}n\text{}[/latex].
How To
Given a function in equation form, write its algebraic formula.
- Solve the equation to isolate the output variable on one side of the equal sign, with the other side as an expression that involves only the input variable.
- Use all the usual algebraic methods for solving equations, such as adding or subtracting the same quantity to or from both sides, or multiplying or dividing both sides of the equation by the same quantity.
Example 4: Finding an Equation of a Function
Express the relationship [latex]\text{}2n+6p=12\text{}[/latex] as a function [latex]\text{}p=f\left(n\right)\text{}[/latex], if possible.
Analysis
It is important to note that not every relationship expressed by an equation can also be expressed as a function with a formula.
Example 5: Expressing the Equation of a Circle as a Function
- Does the equation [latex]\text{}{x}^{2}+{y}^{2}=1\text{}[/latex] represent a function with [latex]\text{}x\text{}[/latex] as input and [latex]\text{}y\text{}[/latex] as output? If so, express the relationship as a function [latex]\text{}y=f\left(x\right)[/latex].
- If [latex]\text{}x-8{y}^{3}=0,\text{}[/latex] express [latex]\text{}y\text{}[/latex] as a function of [latex]\text{}x[/latex].
Question & Answer
Are there relationships expressed by an equation that do represent a function but which still cannot be represented by an algebraic formula?
Yes, this can happen. For example, given the equation [latex]\text{}x=y+{2}^{y},\text{}[/latex] if we want to express [latex]\text{}y\text{}[/latex] as a function of [latex]\text{}x,\text{}[/latex] there is no simple algebraic formula involving only [latex]\text{}x\text{}[/latex] that equals [latex]\text{}y\text{}[/latex]. However, each [latex]\text{}x\text{}[/latex] does determine a unique value for [latex]\text{}y\text{}[/latex], and there are mathematical procedures by which [latex]\text{}y\text{}[/latex] can be found to any desired accuracy. In this case, we say that the equation gives an implicit (implied) rule for [latex]\text{}y\text{}[/latex] as a function of [latex]\text{}x\text{}[/latex], even though the formula cannot be written explicitly.
Evaluating a Function Given in Tabular Form
As we saw above, we can represent functions in tables. Conversely, we can use information in tables to write functions, and we can evaluate functions using the tables. For example, how well do our pets recall the fond memories we share with them? There is an urban legend that a goldfish has a memory of 3 seconds, but this is just a myth. Goldfish can remember up to 3 months, while the beta fish has a memory of up to 5 months. And while a puppy’s memory span is no longer than 30 seconds, the adult dog can remember for 5 minutes. This is meager compared to a cat, whose memory span lasts for 16 hours.
The function that relates the type of pet to the duration of its memory span is more easily visualized with the use of a table. See Table 1-10.[1]
| Pet | Memory span in hours |
|---|---|
| Puppy | 0.008 |
| Adult dog | 0.083 |
| Cat | 16 |
| Goldfish | 2160 |
| Beta fish | 3600 |
At times, evaluating a function in table form may be more useful than using equations. Here let us call the function [latex]P[/latex]. The domain of the function is the type of pet and the range is a real number representing the number of hours the pet’s memory span lasts. We can evaluate the function [latex]\text{}P\text{}[/latex] at the input value of “goldfish.” We would write [latex]P\left(\text{goldfish}\right)=2160[/latex]. Notice that, to evaluate the function in table form, we identify the input value and the corresponding output value from the pertinent row of the table. The tabular form for function [latex]\text{}P\text{}[/latex] seems ideally suited to this function, more so than writing it in paragraph or function form.
How To
Given a function represented by a table, identify specific output and input values.
- Find the given input in the row (or column) of input values.
- Identify the corresponding output value paired with that input value.
- Find the given output values in the row (or column) of output values, noting every time that output value appears.
- Identify the input value(s) corresponding to the given output value.
Example 6: Evaluating and Solving a Tabular Function
Using Table 1-11,
- Evaluate [latex]\text{}g\left(3\right)[/latex].
- Solve [latex]\text{}g\left(n\right)=6[/latex].
- Evaluate [latex]\text{}g\left(1\right)[/latex].
| [latex]n[/latex] | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| [latex]g\left(n\right)[/latex] | 8 | 6 | 7 | 6 | 8 |
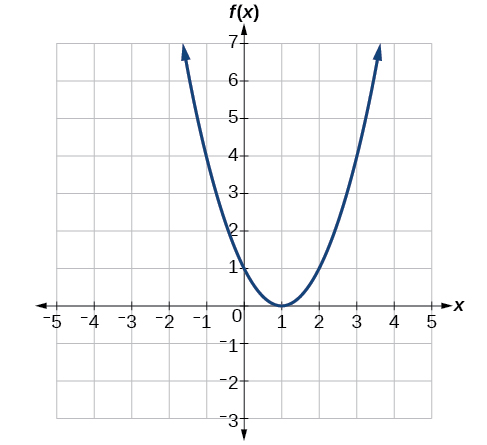
Finding Function Values from a Graph
Evaluating a function using a graph also requires finding the corresponding output value for a given input value, only in this case, we find the output value by looking at the graph. Solving a function equation using a graph requires finding all instances of the given output value on the graph and observing the corresponding input value(s).
Example 7: Reading Function Values from a Graph
Given the graph in Figure 1-4,
- Evaluate [latex](\text{}f\left(2\right)[/latex].
- Solve [latex]\text{}f\left(x\right)=4[/latex].
- Solve [latex]\text{}f\left(x\right)=1[/latex].
Access for free at https://openstax.org/books/precalculus/pages/1-introduction-to-functions
- http://www.kgbanswers.com/how-long-is-a-dogs-memory-span/4221590. Accessed 3/24/2014. ↵
