1.9 Practice Questions
Verbal Questions
- What is the difference between a relation and a function?
- What is the difference between the input and the output of a function?
- Why does the vertical line test tell us whether the graph of a relation represents a function?
- How can you determine if a relation is a one-to-one function?
- Why does the horizontal line test tell us whether the graph of a function is one-to-one?
Algebraic Questions
For the following exercises, determine whether the relation represents a function.
- [latex]\left\{\left(a,b\right),\text{ }\left(c,d\right),\text{ }\left(a,c\right)\right\}[/latex]
- [latex]\left\{\left(a,b\right),\left(b,c\right),\left(c,c\right)\right\}[/latex]
For the following exercises, determine whether the relation represents [latex]\text{}y\text{}[/latex] as a function of [latex]\text{}x\text{}[/latex].
- [latex]5x+2y=10[/latex]
- [latex]y={x}^{2}[/latex]
- [latex]x={y}^{2}[/latex]
- [latex]3{x}^{2}+y=14[/latex]
- [latex]2x+{y}^{2}=6[/latex]
- [latex]y=-2{x}^{2}+40x[/latex]
- [latex]y=\frac{1}{x}[/latex]
- [latex]x=\frac{3y+5}{7y-1}[/latex]
- [latex]x=\sqrt{1-{y}^{2}}[/latex]
- [latex]y=\frac{3x+5}{7x-1}[/latex]
- [latex]{x}^{2}+{y}^{2}=9[/latex]
- [latex]2xy=1[/latex]
- [latex]x={y}^{3}[/latex]
- [latex]y={x}^{3}[/latex]
- [latex]y=\sqrt{1-{x}^{2}}[/latex]
- [latex]x=±\sqrt{1-y}[/latex]
- [latex]y=±\sqrt{1-x}[/latex]
- [latex]{y}^{2}={x}^{2}[/latex]
- [latex]{y}^{3}={x}^{2}[/latex]
For the following exercises, evaluate the function [latex]\text{}f\text{}[/latex] at the indicated values [latex]\text{ }f\left(-3\right),f\left(2\right),f\left(-a\right),-f\left(a\right),f\left(a+h\right)[/latex].
- [latex]f\left(x\right)=2x-5[/latex]
- [latex]f\left(x\right)=-5{x}^{2}+2x-1[/latex]
- [latex]f\left(x\right)=\sqrt{2-x}+5[/latex]
- [latex]f\left(x\right)=\frac{6x-1}{5x+2}[/latex]
- [latex]f\left(x\right)=|x-1|-|x+1|[/latex]
- Given the function [latex]\text{}g\left(x\right)=5-{x}^{2},\text{}[/latex] evaluate [latex]\text{}\frac{g\left(x+h\right)-g\left(x\right)}{h},\text{}h\ne 0[/latex]
- Given the function [latex]\text{}g\left(x\right)={x}^{2}+2x,\text{}[/latex] evaluate [latex]\text{}\frac{g\left(x\right)-g\left(a\right)}{x-a},\text{}x\ne a[/latex]
- Given the function [latex]\text{}k\left(t\right)=2t-1:[/latex]
- Evaluate [latex]\text{}k\left(2\right)[/latex]
- Solve [latex]\text{}k\left(t\right)=7[/latex]
- Given the function [latex]\text{}f\left(x\right)=8-3x:[/latex]
- Evaluate [latex]\text{}f\left(-2\right)[/latex]
- Solve [latex]\text{}f\left(x\right)=-1[/latex]
- Given the function [latex]\text{}p\left(c\right)={c}^{2}+c:[/latex]
- Evaluate [latex]\text{}p\left(-3\right)[/latex]
- Solve [latex]\text{}p\left(c\right)=2[/latex]
- Given the function [latex]\text{}f\left(x\right)={x}^{2}-3x:[/latex]
- Evaluate [latex]\text{}f\left(5\right)[/latex]
- Solve [latex]\text{}f\left(x\right)=4[/latex]
- Given the function [latex]\text{}f\left(x\right)=\sqrt{x+2}:[/latex]
- Evaluate [latex]\text{}f\left(7\right)[/latex]
- Solve [latex]\text{}f\left(x\right)=4[/latex]
- Consider the relationship [latex]\text{}3r+2t=18[/latex]
- Write the relationship as a function [latex]\text{}r=f\left(t\right)[/latex]
- Evaluate [latex]\text{}f\left(-3\right)[/latex]
- Solve [latex]\text{}f\left(t\right)=2[/latex]
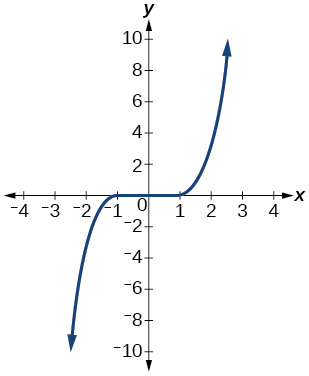
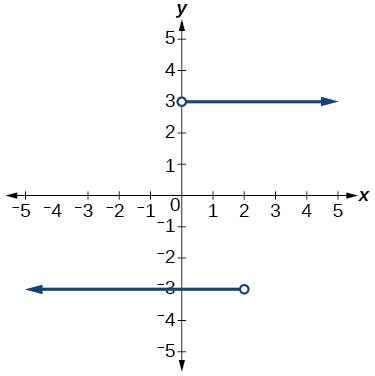
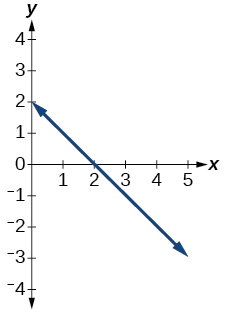
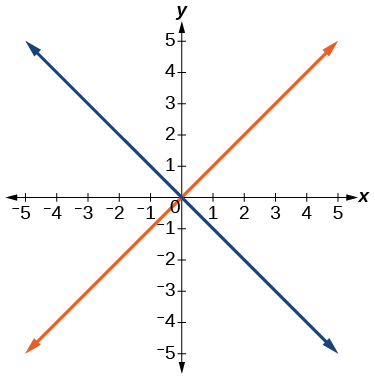
Graphical Questions
Numeric Questions
For the following exercises, determine whether the relation represents a function.
- [latex]\left\{\left(-1,-1\right),\left(-2,-2\right),\left(-3,-3\right)\right\}[/latex]
- [latex]\left\{\left(3,4\right),\left(4,5\right),\left(5,6\right)\right\}[/latex]
- [latex]\left\{\left(2,5\right),\left(7,11\right),\left(15,8\right),\left(7,9\right)\right\}[/latex]
For the following exercises, determine if the relation represented in table form represents [latex]\text{}y\text{}[/latex] as a function of [latex]\text{}x[/latex].
-
[latex]x[/latex] 5 10 15 [latex]y[/latex] 3 8 14 -
[latex]x[/latex] 5 10 15 [latex]y[/latex] 3 8 8 -
[latex]x[/latex] 5 10 10 [latex]y[/latex] 3 8 14
For the following exercises, use the function [latex]\text{}f\text{}[/latex] represented in Table 1-14.
| [latex]x[/latex] | [latex]f\left(x\right)[/latex] |
|---|---|
| 0 | 74 |
| 1 | 28 |
| 2 | 1 |
| 3 | 53 |
| 4 | 56 |
| 5 | 3 |
| 6 | 36 |
| 7 | 45 |
| 8 | 14 |
| 9 | 47 |
- Evaluate [latex]\text{}f\left(3\right)[/latex].
- Solve [latex]\text{}f\left(x\right)=1[/latex].
For the following exercises, evaluate the function [latex]\text{}f\text{}[/latex] at the values [latex]f\left(-2\right),\text{}f\left(-1\right),\text{}f\left(0\right),\text{}f\left(1\right)[/latex] and [latex]\text{}f\left(2\right)[/latex].
- [latex]f\left(x\right)=4-2x[/latex]
- [latex]f\left(x\right)=8-3x[/latex]
- [latex]f\left(x\right)=8{x}^{2}-7x+3[/latex]
- [latex]f\left(x\right)=3+\sqrt{x+3}[/latex]
- [latex]f\left(x\right)=\frac{x-2}{x+3}[/latex]
- [latex]f\left(x\right)={3}^{x}[/latex]
For the following exercises, evaluate the expressions, given functions [latex]f,\text{}\text{}g[/latex], and [latex]\text{}h:[/latex]
- [latex]f\left(x\right)=3x-2[/latex]
- [latex]g\left(x\right)=5-{x}^{2}[/latex]
- [latex]h\left(x\right)=-2{x}^{2}+3x-1[/latex]
- [latex]3f\left(1\right)-4g\left(-2\right)[/latex]
- [latex]f\left(\frac{7}{3}\right)-h\left(-2\right)[/latex]
Technology Questions
For the following exercises, graph [latex]\text{}y={x}^{2}\text{}[/latex] on the given viewing window. Determine the corresponding range for each viewing window. Show each graph.
- [latex]\left[-0.1,\text{ }0.1\right][/latex]
- [latex]\left[-10,\text{ 10}\right][/latex]
- [latex]\left[-100,100\right][/latex]
For the following exercises, graph [latex]\text{}y={x}^{3}\text{}[/latex] on the given viewing window. Determine the corresponding range for each viewing window. Show each graph.
- [latex]\left[-0.1,\text{ 0}\text{.1}\right][/latex]
- [latex]\left[-10,\text{ 10}\right][/latex]
- [latex]\left[-100,\text{ 100}\right][/latex]
For the following exercises, graph [latex]\text{}y=\sqrt{x}\text{}[/latex] on the given viewing window. Determine the corresponding range for each viewing window. Show each graph.
- [latex]\left[0,\text{ 0}\text{.01}\right][/latex]
- [latex]\left[0,\text{ 100}\right][/latex]
- [latex]\left[0,\text{ 10,000}\right][/latex]
For the following exercises, graph [latex]y=\sqrt[3]{x}[/latex] on the given viewing window. Determine the corresponding range for each viewing window. Show each graph.
- [latex]\left[-0.001,\text{0.001}\right][/latex]
- [latex]\left[-1000,\text{1000}\right][/latex]
- [latex]\left[-1,000,000,\text{1,000,000}\right][/latex]
Real-World Applications Questions
- The amount of garbage, [latex]\text{}G,\text{}[/latex] produced by a city with population [latex]\text{}p\text{}[/latex] is given by [latex]\text{}G=f\left(p\right)\text{}[/latex]. [latex]G\text{}[/latex] is measured in tons per week, and [latex]\text{}p\text{}[/latex] is measured in thousands of people.
- The town of Tola has a population of 40,000 and produces 13 tons of garbage each week. Express this information in terms of the function [latex]\text{}f\text{}[/latex].
- Explain the meaning of the statement [latex]\text{}f\left(5\right)=2[/latex].
- The number of cubic yards of dirt, [latex]\text{}D,\text{}[/latex] needed to cover a garden with area [latex]\text{}a\text{}[/latex] square feet is given by [latex]\text{}D=g\left(a\right)[/latex].
- A garden with area 5000 ft2 requires 50 yd3 of dirt. Express this information in terms of the function [latex]\text{}g[/latex].
- Explain the meaning of the statement [latex]\text{}g\left(100\right)=1[/latex].
- Let [latex]\text{}f\left(t\right)\text{}[/latex] be the number of ducks in a lake [latex]\text{}t\text{}[/latex] years after 1990. Explain the meaning of each statement:
- [latex]f\left(5\right)=30[/latex]
- [latex]f\left(10\right)=40[/latex]
- Let [latex]\text{}h\left(t\right)\text{}[/latex] be the height above ground, in feet, of a rocket [latex]\text{}t\text{}[/latex] seconds after launching. Explain the meaning of each statement:
- [latex]h\left(1\right)=200[/latex]
- [latex]h\left(2\right)=350[/latex]
- Show that the function [latex]\text{}f\left(x\right)=3{\left(x-5\right)}^{2}+7\text{}[/latex] is not one-to-one.
Access for free at https://openstax.org/books/precalculus/pages/1-introduction-to-functions