1.1 Introduction to Functions and Function Notation

A jetliner changes altitude as its distance from the starting point of a flight increases. The weight of a growing child increases with time. In each case, one quantity depends on another. There is a relationship between the two quantities that we can describe, analyze, and use to make predictions. In this section, we will analyze such relationships.

Introduction to Functions

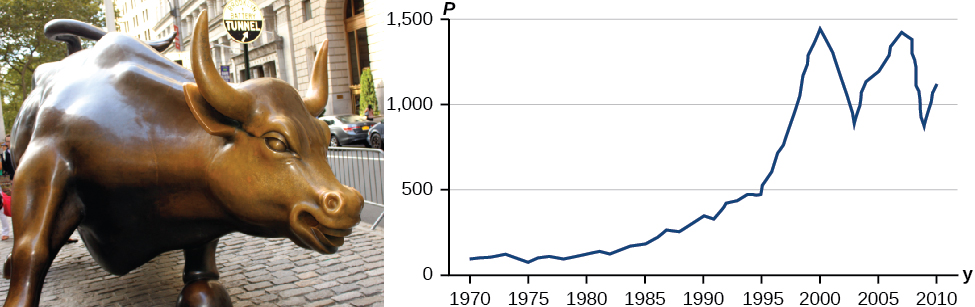
Toward the end of the twentieth century, the values of stocks of internet and technology companies rose dramatically. As a result, the Standard and Poor’s stock market average rose as well. Figure 1-1 tracks the value of that initial investment of just under $100 over the 40 years. It shows that an investment that was worth less than $500 until about 1995 skyrocketed up to about $1,100 by the beginning of 2000. That five-year period became known as the “dot-com bubble” because so many internet startups were formed. As bubbles tend to do, though, the dot-com bubble eventually burst. Many companies grew too fast and then suddenly went out of business. The result caused the sharp decline represented on the graph beginning at the end of 2000.

Notice, as we consider this example, that there is a definite relationship between the year and stock market average. For any year we choose, we can determine the corresponding value of the stock market average. In this chapter, we will explore these kinds of relationships and their properties.

Overview

The following video (11:33) provides a short overview of functions, domain and range which will be covered in this section (1 – Introduction to Functions) and the next section (2 – Domain and Range).

Access for free at https://openstax.org/books/precalculus/pages/1-introduction-to-functions