10 Enzyme Kinetics & The Michaelis-Menten Equation
Synopsis: We can gain some understanding of enzyme behaviour through the study of rates of enzyme-catalyzed reactions and by the mathematical analysis of their rate, known as enzyme kinetics. Simple measures of enzyme reactions include activity, specific activity (activity per unit mass) and turnover number (activity per mole of enzyme). Turnover number also represents the actual number of times an enzyme molecule reacts per second.
Enzyme kinetics studies how rates of enzyme-catalyzed reactions depend on the concentrations of substrates. Enzyme reactions do not show simple zero, first or second order relationships of chemical reactions. Instead the reaction reaches a limiting or saturation rate. This behaviour is governed by the Michaelis-Menten equation and the two characteristic constants associated with this equation are Vmax and KM.
Quantitative description of enzyme catalysis
Or = concentration of product produced per unit time (mol L–1 sec–1)
Enzyme activity = moles of substrate converted per unit time = rate x reaction volume
Enzyme activity is a measure of quantity of enzyme present. The SI unit is the katal, 1 katal = 1 mol s–1, but this is an excessively large unit. A more practical value is 1 enzyme unit (EU) = 1 µmol min–1 (µ = micro, 10-6).
Specific activity = moles of substrate converted per unit time per unit mass of enzyme
= enzyme activity / actual mass of enzyme present
SI units: katal kg–1; Practical units: µmol mg–1 min–1 or µmol µg–1min–1.
Specific activity is a measure of enzyme efficiency, usually constant for a pure enzyme.
If the specific activity of 100% pure enzyme is known, then an impure sample will have a lower specific activity, allowing purity to be calculated.
![]()
The impure sample has lower specific activity because some of the mass is not actually enzyme.
![]() (usually per second).
(usually per second).
= specific activity x molar mass of enzyme (with necessary unit conversions!)
Multiplying mass by molar mass converts specific activity (per unit mass) into activity per mole.
If n moles of substrate are catalyzed by one mole of enzyme per second, then n molecules of substrate are catalysed by each molecule of enzyme per second.
Hence turnover number represents the number of times per second that the enzyme completes a reaction cycle.
Sample calculations:
A solution contains initially 25.0 × 10–4 mol L–1 of peptide substrate and 1.50 µg chymotrypsin, in 2.5 mL volume. After 10 minutes, 18.6 × 10–4 mol L–1 of peptide substrate remains. Molar mass of chymotrypsin is 25,000 g mol–1.
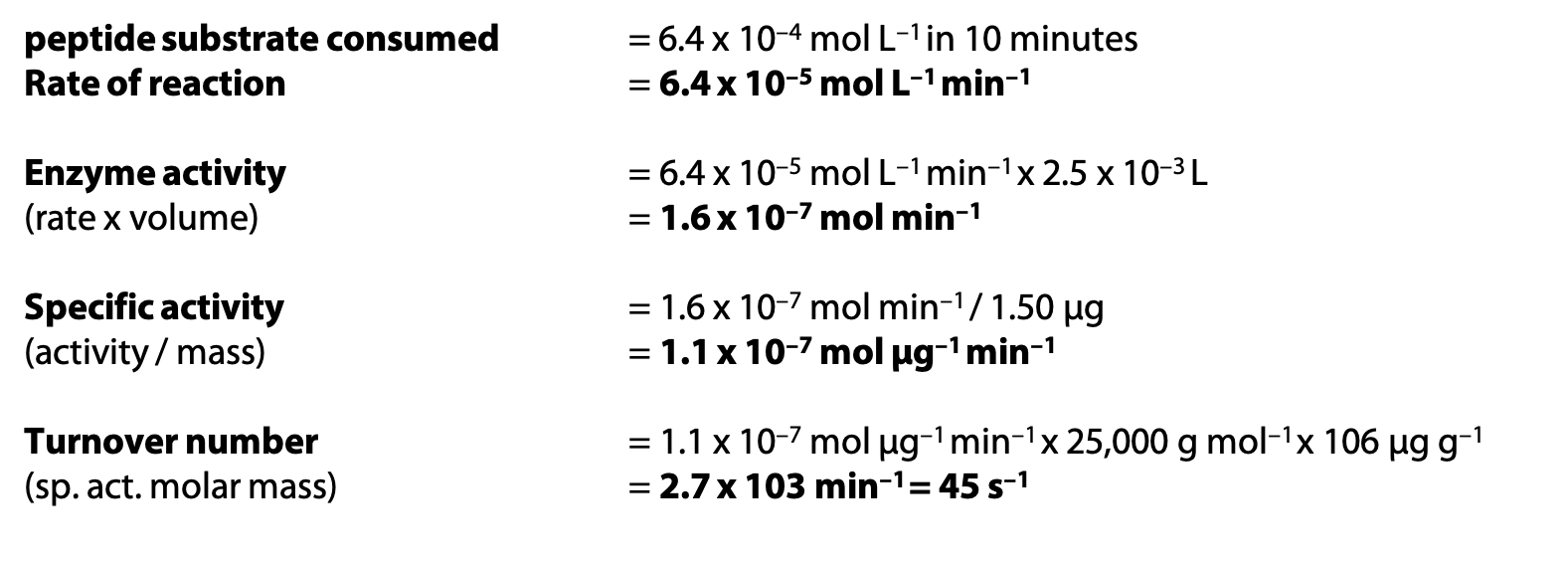 If the specific activity calculated above refers to pure chymotrypsin, and another sample of chymotrypsin is found to have specific activity 2.0 x 10–8 mol µg–1 min–1, what is the purity of the second sample?
If the specific activity calculated above refers to pure chymotrypsin, and another sample of chymotrypsin is found to have specific activity 2.0 x 10–8 mol µg–1 min–1, what is the purity of the second sample?
![]()
1.0 µg of sample actually has only 0.18 µg active chymotrypsin and 0.82 µg other impurities.
Enzyme kinetics
Reaction rate and chemical kinetics
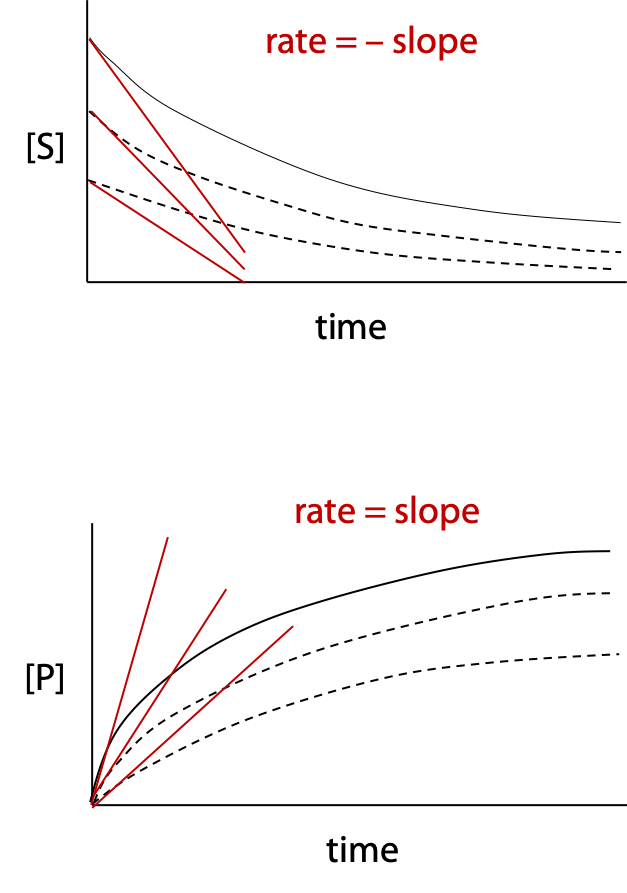
If decrease in substrate concentration or increase in product concentration is measured over a period of time for an enzyme-catalyzed reaction, the data can be plotted as a curve called the progress curve (Figure 10.1).
Reaction rate is the slope of the curve. The initial reaction rate is given the symbol vo, which is the tangent to the progress curve at time zero (negative tangent if disappearance of reactant is measured). Some enzyme reactions remain linear for a significant time, making slope measurement easier; some reactions follow curves as in the examples.
If several experiments are run, with a different initial concentration of substrate, each experiment produces a different progress curve with one value of initial rate vo for each curve measured.
The initial rates are then plotted as a function of initial substrate concentration [S]. Normal chemical reactions follow simple rate laws, which describe how rate varies as a function of reactant or substrate concentration (Figure 10.2).

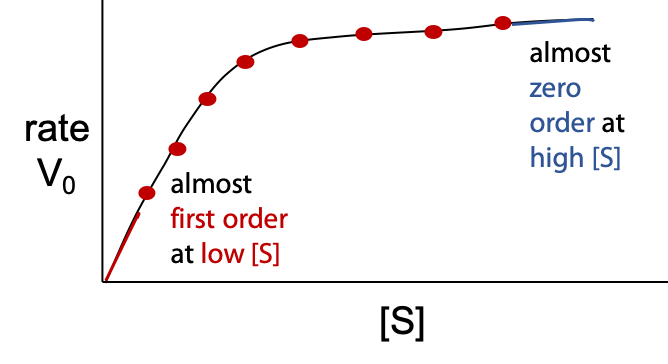
The enzyme-catalyzed reaction does not follow a simple rate law (Figure 10.3):
Although vo is directly proportional to [E], concentration of enzyme, initial rate vo is a complex function of [S] – substrate concentration.
Interpretation of initial velocity dependence on [S]
The mathematical relationship between initial velocity and [S] was first worked out by Henri (1905, France), and subsequently verified experimentally by Michaelis and Menten (USA/Canada, 1913). Henri, Michaelis and Menten all assumed that the binding step was at equilibrium, which is only an approximation. Briggs and Haldane described a more accurate derivation of the equation in 1926 that follows below.
Although the overall reaction appears to be S→P, the underlying process is more complex and can be interpreted as a two-step reaction (Figure 10.4).
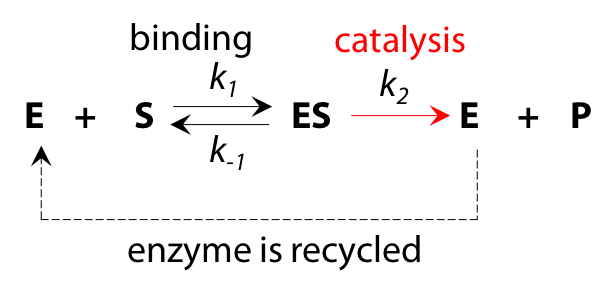
- The enzyme is a catalyst and is recycled in an unchanged state by the end of the reaction process, so the total quantity of enzyme [E]total does not change as reaction proceeds.
- If we deal only with initial reaction rate vo, when product P is not yet present, there will be no reverse reaction ES → E + P at the catalytic step to complicate matters. Omitting this reverse reaction will make the algebra more manageable.
- Each stage in the reaction has an associated rate constant, k1, k2 and k–1 for the reverse of step 1. k2 is sometimes described as kcat, the rate constant for catalysis.
The rate of appearance of product P describes the overall rate of the complete enzyme reaction. It can be determined by taking the rate of step 2, which is a fundamental chemical process, for which we can write the first order rate equation:
vo = k2 [ES]
where [ES] is the concentration of enzyme actually occupied by substrate.
Although we know [E]total, because that’s how much enzyme we put into the reaction, we don’t explicitly know what fraction of enzyme is empty E and what fraction is occupied ES, so [E] and [ES] are unknown values, but related by the equation [E]total = [E] + [ES]. (Conservation of Mass).
We can determine [ES] algebraically
We can write the fundamental rate equations for formation and breakdown of ES.
Rate of formation of ES = k1[E][S]
Rate of breakdown of ES = k2[ES] + k–1[ES] (forward component + reverse component)
The steady state condition of Briggs and Haldane states that
rate of breakdown = rate of formation
If the rate of breakdown happens to be greater than the rate of formation, [ES] will decrease, causing the rate of breakdown to slow down. If the rate of breakdown happens to be less than the rate of formation, [ES] will increase, causing the rate of breakdown to speed up. Hence the two rates rapidly tend to match each other.Thus, we can write:
(k2 + k–1)[ES] = k1[E][S]
Divide by k1 to put all the constants on the left, and replace ![]()
KM[ES] = [E][S] but both [ES] and [E] are unknown.
Now use the relationship [E] = [E]total – [ES] to eliminate the second unknown value [E]
KM[ES] = ([E]total – [ES]) [S]
then take the term [ES][S] over to the left side
(KM + [S]) [ES] = [E]total[S]
where [E]total and [S] are known values, and KM is a constant
This is used to replace the [ES] in the rate equation vo = k2[ES]
![]()
The maximum observable rate Vmax occurs when 100% of the enzyme is occupied by substrate, so [ES]max = [E]total where [E]total is a measurable quantity.
Thus we can write Vmax = k2[E]total and replace k2[E]total in the equation above with Vmax to get the Michaelis-Menten equation
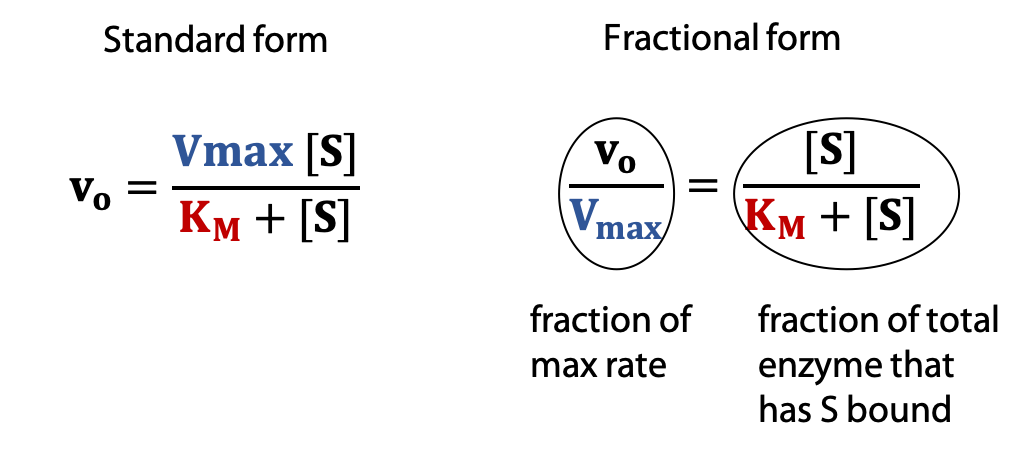
The Michaelis-Menten equation shows how vo varies as a function of substrate concentration [S], in terms of two constants, Vmax and KM.
Every enzyme has characteristic values of KM and Vmax that describe its catalytic behaviour.
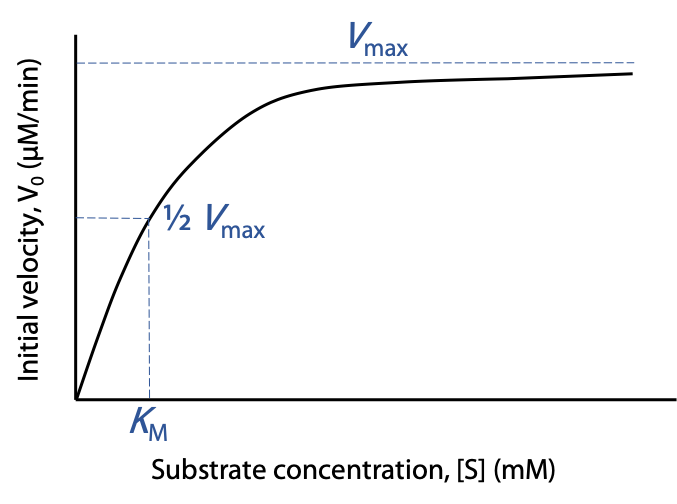
Vmaxis the theoretical upper limit for the observed rate, where the kinetic curve levels off at high [S] (Figure 10.5):
When vo approaches Vmax, almost all of the enzyme is in the occupied ES state, and the enzyme is said to be saturated with substrate.
The Michaelis constant KM is the concentration of substrate needed to give a rate of exactly 0.5 Vmax. [S] = KM when vo = 0.5 Vmax
KM has units of concentration, and typical KM values are between 10-6 M and 10-2 M.
Low KM indicates that the enzyme binds and utilizes the substrate well; a lower [S] is sufficient to occupy the enzyme.
A high KM indicates that the enzyme binds and utilizes the substrate poorly; a higher [S] is needed to get S to occupy the enzyme.
Calculations based on Michaelis-Menten equation
If the enzyme phosphatase has KM = 2.0 × 10–4 M and its substrate p-nitrophenyl phosphate is present at 5.0 × 10–4 M, find the rate of reaction a) as a fraction of Vmax; and b) if Vmax = 5.0 × 10–8 M .s–1
a) calculating vo as a fraction of Vmax.
![]()
![]()
= 0.71
b) calculating vo for a given value of Vmax = 5.0 × 10–8 M .s–1
v0 = 0.71 x Vmax
= 0.71 x 5.0 x 10-8 M.s-1
= 3.5 x 10-8 M.s-1
If glucosidase has KM = 6.0 x 10–5 M, what value of [S] is needed to get a) vo = 0.75 Vmax and b) vo = 4.0 x 10–9 M .s–1 given Vmax = 2.0 x 10–8 M .s–1
a) ![]()
0.75(KM + [S]) = [S]
0.75KM = 0.25[S]
[S] = 3KM
[S] = 1.8 x 10-4 M
b) ![]()
0.20(KM + [S]) = [S]
0.20KM = 0.80[S]
[S] = 0.25KM
[S] = 1.5 x 10-5 M
If [S] = 0.5 KM, what is vo, expressed as a fraction of Vmax?
![]()
= ![]()
= 0.33 Vmax
If vo/Vmax = 0.86, what is [S], expressed as a multiple of KM?
![]()
0/86(KM + [S]) = [S]
0.86KM = 0.14[S]
[S] = 6.1KM
Note that vo can never be greater than Vmax, but [S] may have any value, which may be much greater than KM.
