Oxidation –reduction reactions

Here’s a review of oxidation/reduction (redox) chemistry. Consult your first-year chemistry textbook for further explanation.

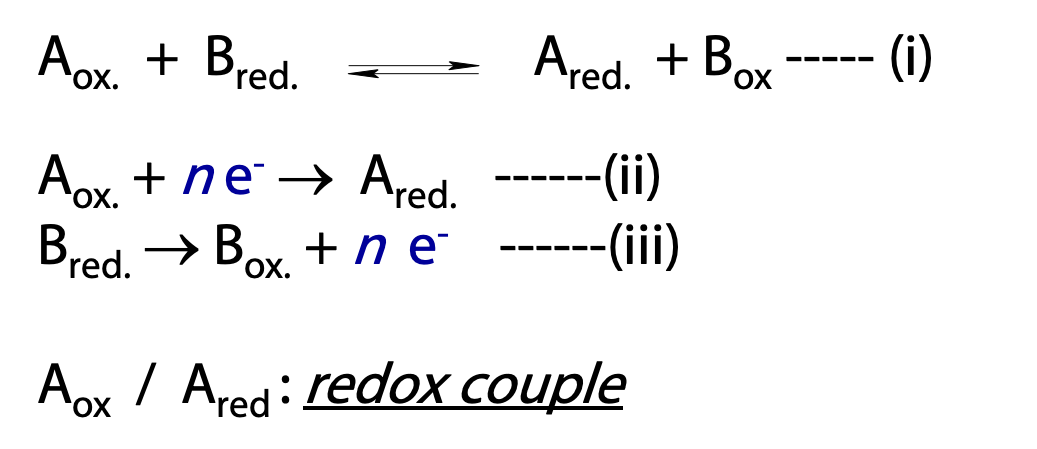
Oxidation and reduction reactions must occur together (reaction (i, Figure 18.1)), however it is easier to consider the two halves separately when describing electron transfers (reaction (ii) and (iii)).

The electron donating molecule in an oxidation reduction reaction (B_red) is called the reducing agent or reductant; the electron accepting molecule (A_ox) is the oxidizing agent or oxidant.

Where would the equilibrium of a redox reaction lie?

How could we decide in which direction the equilibrium of this reaction lies? Will it be A_ox or B_ox that will be accepting the available electrons? Will the reaction proceed in the forward or the reverse direction?

We can determine this by comparing the standard reduction potential (E˚^′) of the two half reactions.

E˚ = Standard Reduction Potential

E˚^′ = Standard Reduction Potential at pH 7 and 25˚C.

Biochemists use the transformed standard reduction potential (E˚^′), as the standard state in biochemistry is defined as pH 7 (Similar to the definition of ΔG˚^′).

 

Measuring the Standard Reduction Potential of half reactions (E˚^′)

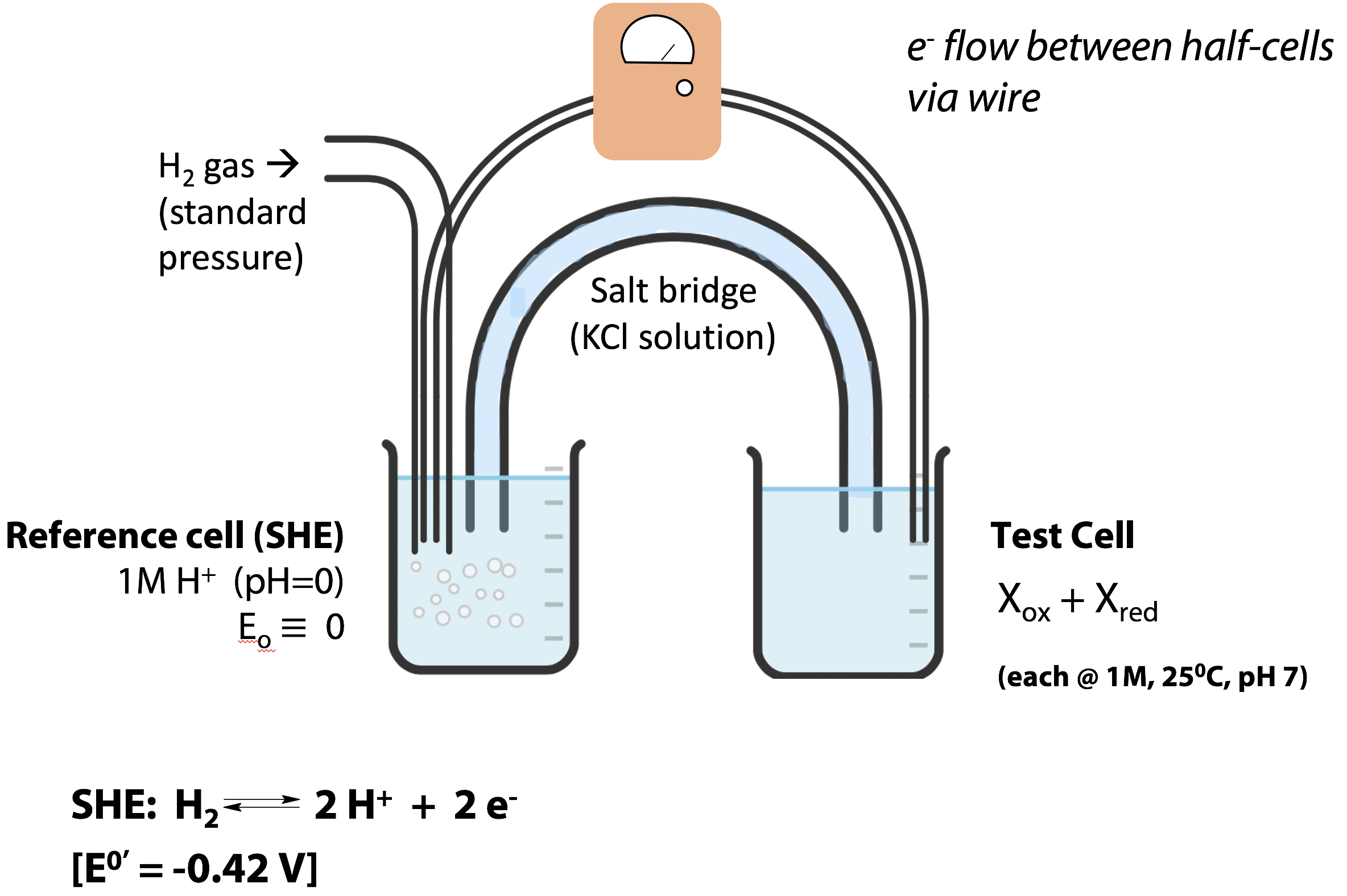
Redox potentials can be measured with an electrochemical cell apparatus (Figure 18.2). Each cell mediates one of the half-reactions, and the electrons pass between the cells through a wire. A potentiometer measures the electrical potential difference. The modern reference half-cell, for which the reduction potential is defined to be zero, is the “standard hydrogen electrode” (SHE) at pH 0 (1 M H⁺), which mediates the half-reaction:

H₂   ↔ 2H⁺ + 2e^–

The test cell contains 1M concentrations of the oxidized and reduced species of the redox couple to be tested, at pH 7 and 25˚C. (E˚^′ for the SHE is measured to be -0.42 V. It can be measured by connecting the 2H⁺/H₂ pair at pH 7 in the test cell to the SHE at pH 0).

A setup like the one shown in Figure 18.2 won’t work very well for most biochemicals, especially proteins. Proteins are not adapted to transfer electrons through metal wires. The redox-active catalytic centre of a protein is buried deep inside the molecule, at the active site – it would not even make electrical contact with a wire electrode. So, for proteins, we usually add a small (catalytic) amount of a redox-active dye, which can transfer electrons between the protein and the metal electrode.

Once the standard reduction potential of each of the half reactions is known, we can predict the direction in which electrons will flow when two half cells are connected through an external wire or when the components of the two half cells are present in a single solution. Electrons will always flow to the half-cell with the higher reduction potential (more positive E˚^′) and the strength of that tendency will be proportional to ΔE˚^′ (see next page for calculation of ΔE^˚′)_.

Let’s answer the following question. Can fumarate oxidize cysteine? (i.e., will the reaction below proceed in the forward direction with fumarate oxiding cysteine or in the reverse direction with cystine oxidizing succinate?)

2 cysteine + fumarate ↔ cystine + succinate

In order to determine the direction of this reaction, we have to first identify the oxidant (fumarate or cystine) that will act as the electron acceptor. Note: both half reactions below are written as reductions. Therefore, you will be able to identify the oxidized and the reduced species of each redox couple. Fumarate and cystine (on the left) are the oxidized species of each redox couple (oxidents/oxidizing agents). Succinate and cysteine (on the right) are the reduced species (reductants or reducing agents).

fumarate + 2 H⁺ + 2e^– ↔ succinate        +0.03 V        (i)

cystine + 2 H⁺ + 2e^– ↔ 2 cysteine            -0.34 V         (ii)

Since fumarate has the higher reduction potential, it would be the electron acceptor in this reaction. Reaction ii; therefore, will not proceed in the direction written. It will give up electrons (reaction iii).

2 cysteine ↔ cystine + 2H⁺ + 2e^–              +0.34 V       (iii)

With the change in the direction of the half reaction, the value of E would also move from -0.34 to + 0.34. Now we can add reaction i and iii to give the final redox reaction. The ΔE^˚′ for the reaction is calculated by adding the E of reaction i and iii.

2 cysteine + fumarate → cystine + succinate          +0.37 V       (i + iii)

The reaction will proceed spontaneously if ΔE˚^′ > 0

Since the ΔE˚′ for the above example is +0.37, the reaction will proceed spontaneously in the forward direction. Therefore, fumarate will oxidize cysteine (alternately, you can also describe the reaction as cysteine reducing fumarate).

(Another way to find out ΔE˚′ is by subtracting the E˚′ for the electron donor from the E˚′ of the electron acceptor. For example, in the above example ΔE˚′ = +0.03 – (-0.34) = +0.37 V)

ΔE˚′ = E˚′ of the electron acceptor – E˚′ of the electron donor

Note: You would see that the ΔE˚′ for the reverse reaction gives a negative value

ΔE˚′ = -0.34 – (0.03) = -0.37 V), indicating that the reverse reaction will not be spontaneous under these conditions.

Once we know ΔE˚′, we can calculate the ΔG˚′ for the redox reaction. You can see from the above equation that the energy made available by the electron flow (the free energy change, ΔG˚′ for the oxidation-reduction reaction) is proportional to ΔE˚′.

Electrons always flow from a redox pair with a lower E˚′ to a redox pair with a higher E˚′.
This is the table shown in Lehninger Principles of Biochemistry (Figure 18.3). The couples with the more positive reduction potentials are the strong oxidants (O₂ being the strongest); couples with the more negative reduction potentials are the strong reductants. By comparing the reduction potentials you can see that NADH is a stronger reducing agent than FADH₂ and FAD is a stronger oxidizing agent than NAD⁺.