4.4 Equivalent Payments
LEARNING OBJECTIVES
- Calculate equivalent payments that replace another payment or a set of payments.
Unforeseen events and circumstances can force you to rearrange your financial commitments. When this happens, the new deal has to be fair to all parties concerned.
For example, suppose you and your co-workers rely on your company’s annual Christmas bonuses. However, the CEO just announced that because of tough economic conditions no one will get a bonus this year. You already earmarked that money to pay a $5,000 debt due next week. You want to be financially responsible, but you cannot possibly make the payment. Before picking up the phone to call your creditor, you need to determine what course of action you should pursue. You need to make alternative arrangements that leave your creditor in the same financial position as the original agreement did. You saw in the previous section that if you were going to make an early payment, the payment should be reduced by an agreed-upon discount rate. In this case, though, you are going to make a late payment, so you must grant the creditor interest. Thus, if you propose paying the debt six months late and your creditor agrees to 9% compounded monthly as a fair rate, then you owe $5,229.26.
This concept applies to all aspects of your personal and professional life. Except for gifts, personal debts to friends or family members should bear some interest. Everyone should be financially fair to each other. A business must be willing to work with its clients in the event they need to alter an agreement. A company that is inflexible tends to find itself writing off bad debt or pursuing unpleasant and sometimes expensive legal action. This section explores the concept of equivalent payment streams, which involves equating two or more alternative financial streams to ensure that neither party is penalized by any choice.
The Fundamental Concept of Equivalency
The fundamental concept of equivalency states that two or more payment streams are equal to each other if they have the same economic value on the same focal date. As illustrated in the figure below, the two alternative financial streams are equivalent if the total of Payment Stream 1 is equal to the total of Payment Stream 2 on the same focal date.
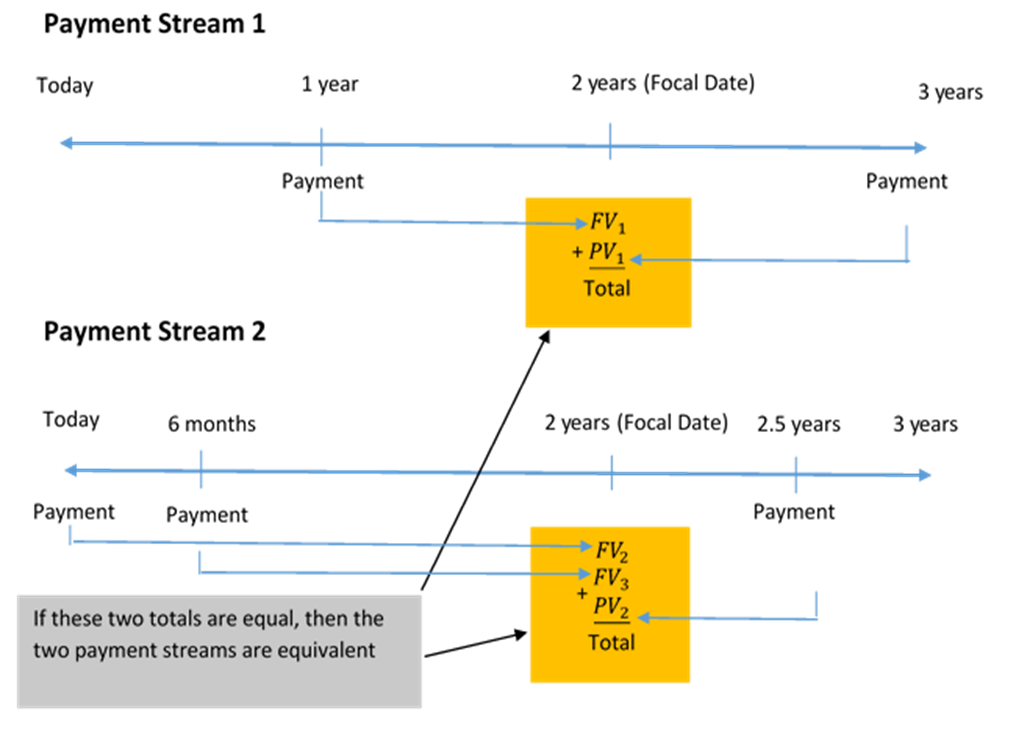
Replacing a Series of Payment with a Single Equivalent Payment
In this first situation, you are going to replace a series of payments with one single payment that is equivalent to the original series of payments. To find the single payment, follow these steps.
- Draw a timeline, in chronological order, to show the original series of payments along with the times the payments were supposed to be made. Clearly indicate the dates of the payments and the payment amounts.
- For a single equivalent payment calculation, choose the date of the single payment as the focal date.
- Move all of the payments from the original series of payments to the focal date using a future value or present value calculation.
- If the payment is moving forward in time to get to the focal date, the payment is a present value and you need to find its future value at the focal date.
- If the payment is moving backward in time to get to the focal date, the payment is a future value and you need to find its present value at the focal date.
- The single equivalent payment is the sum of the payments at the focal date.
EXAMPLE
Assume you owe $1,000 today and $1,000 one year from now. You find yourself unable to make that payment today, so you indicate to your creditor that you want to make both payments six months from now instead. Prevailing interest rates are at 6% compounded semi-annually. What single payment six months from now (the new payment stream) is equivalent to the two payments (the original payment stream)?
Solution:
Step 1: Draw the timeline.

Step 2: Choose six months from today as the focal date.
Step 3: Calculate the future value of the $1,000 payment today at the focal date. Because this payment must move forward in time to get to the focal date, the $1,000 is a present value and its value at the focal date is a future value. This payment must move 6 months (from today to 6 months from today) to get to the focal date, so the time for the future value calculation is 6 months or 0.5 year.
| N | [latex]2 \times 0.5=1[/latex] |
| PV | [latex]-1,000[/latex] |
| FV | ? |
| PMT | [latex]0[/latex] |
| I/Y | [latex]6[/latex] |
| P/Y | [latex]2[/latex] |
| C/Y | [latex]2[/latex] |
[latex]\displaystyle{FV=\$1,030}[/latex]
Step 4: Calculate the present value of the $1,000 payment one year from now at the focal date. Because this payment must move backward in time to get to the focal date, the $1,000 is a future value and its value at the focal date is a present value. This payment must move 6 months (from 1 year from today to 6 months from today) to get to the focal date, so the time for the present value calculation is 6 months or 0.5 year.
| N | [latex]2 \times 0.5=1[/latex] |
| PV | ? |
| FV | [latex]-1,000[/latex] |
| PMT | [latex]0[/latex] |
| I/Y | [latex]6[/latex] |
| P/Y | [latex]2[/latex] |
| C/Y | [latex]2[/latex] |
[latex]\displaystyle{PV=\$970.87}[/latex]
Step 5: The single equivalent payment is the sum of the payments at the focal date.
[latex]\begin{eqnarray*} \mbox{Single Payment} & = & 1,030+970.87 \\ & = & \$2,000.87 \end{eqnarray*}[/latex]
A single payment of $2,000.87 six months from now is equivalent to the original payments of $1,000 today and $1,000 one year from now.
NOTES
- A properly drawn timeline, in chronological order, can help you see what you need to do, where the payments need to go (in relation to the focal date), and whether you need to do a future value or present value calculation to move the payments to the focal date.
- Any date can be chosen as the focal date. But in a single equivalent payment calculation you need to know the value of the single payment at the focal date, so it makes sense to choose the time of the single payment as the focal date.
- To find the time a payment has to move from its current date to the focal date, use the following technique.
- If the date of the payment and the focal date are on the same side as today, subtract the times. For example, if the original payment is at 2 years from today and the focal date is at 5 years from today, the time the original payment has to move to get to the focal date is 5-2=3 years.
- If the date of the payment and the focal date are on opposite sides of today, add the times. For example, if the original payment is at 3 years ago and the focal date is 4 years from today, the time the original payment has to move to get to the focal date is 3+4=7 years.
- Treat today as time 0.
EXAMPLE
Johnson’s Garden Centre has recently been unprofitable and concludes that it cannot make two debt payments of $4,500 due today and another $6,300 due in three months. After discussions between Johnson’s Garden Centre and its creditor, the two parties agree that both payments could be made nine months from today, with interest at 8.5% compounded monthly. What total payment does Johnson’s Garden Centre need nine months from now to clear its debt?
Solution:
Step 1: Draw the timeline.
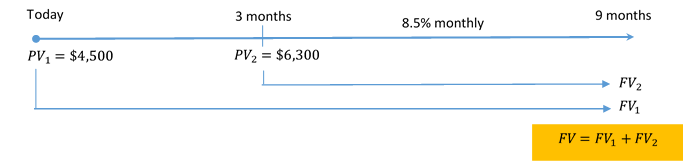
Step 2: Choose nine months from today as the focal date.
Step 3: Calculate the future value of the $4,500 payment today at the focal date. Because this payment must move forward in time to get to the focal date, the $4,500 is a present value and its value at the focal date is a future value. This payment must move 9 months (from today to 9 months from today) to get to the focal date, so the time for the future value calculation is 9 months or 0.75 year.
| N | [latex]12 \times 0.75=9[/latex] |
| PV | [latex]-4,500[/latex] |
| FV | ? |
| PMT | [latex]0[/latex] |
| I/Y | [latex]8.5[/latex] |
| P/Y | [latex]12[/latex] |
| C/Y | [latex]12[/latex] |
[latex]\displaystyle{FV_1=\$4,795.14}[/latex]
Step 4: Calculate the future value of the $6,300 payment today at the focal date. Because this payment must move forward in time to get to the focal date, the $6,300 is a present value and its value at the focal date is a future value. This payment must move 6 months (from 3 months from today to 9 months from today) to get to the focal date, so the time for the future value calculation is 6 months or 0.5 year.
| N | [latex]12 \times 0.5=6[/latex] |
| PV | [latex]-6,300[/latex] |
| FV | ? |
| PMT | [latex]0[/latex] |
| I/Y | [latex]8.5[/latex] |
| P/Y | [latex]12[/latex] |
| C/Y | [latex]12[/latex] |
[latex]\displaystyle{FV_2=\$6,572.54}[/latex]
Step 5: The single equivalent payment is the sum of the payments at the focal date.
[latex]\begin{eqnarray*} \mbox{Single Payment} & = & 4,795.14+6,572.54 \\ & = & \$11,367.68 \end{eqnarray*}[/latex]
A single payment of $11,367.68 nine months from now is equivalent to the original payments of $4,500 today and $6,300 three months from now.
TRY IT
What single payment in 2 years would replace payments of $5,000 due 1.5 years ago, $2,500 due in 1 year, and $1,000 due in 4 years if money earns 3.5% compounded quarterly?
Click to see Solution
Using 2 years as the focal date:
| N | [latex]14[/latex] | [latex]4[/latex] | [latex]8[/latex] |
| PV | [latex]-5,000[/latex] | [latex]-2,500[/latex] | [latex]\textcolor{blue}{932.68}[/latex] |
| FV | [latex]\textcolor{blue}{5,648.59}[/latex] | [latex]\textcolor{blue}{2,588.66}[/latex] | [latex]-1,000[/latex] |
| PMT | [latex]0[/latex] | [latex]0[/latex] | [latex]0[/latex] |
| I/Y | [latex]3.5[/latex] | [latex]3.5[/latex] | [latex]3.5[/latex] |
| P/Y | [latex]4[/latex] | [latex]4[/latex] | [latex]4[/latex] |
| C/Y | [latex]4[/latex] | [latex]4[/latex] | [latex]4[/latex] |
[latex]\begin{eqnarray*} \mbox{Single Payment} & = & 5,648.59+2,588.66+932.68 \\ & = & \$9,169.93 \end{eqnarray*}[/latex]
Replacing a Series of Payments with an Equivalent Series of Payments
In this situation, you are going to replace a series of payments with another series of payments that is equivalent to the original series of payments. To find the new series payment, follow these steps.
- Draw a timeline, in chronological order, to show the original series of payments and the new series of payments, along with the times the payments were supposed to be made. Clearly indicate the dates of the payments and the payment amounts. To keep track of which payment belongs to which payment stream, draw the timeline in different colours or draw multiple timelines, one for each payment stream.
- Select a focal date.
- Move all of the payments (from both the original payment stream and the new payment stream) to the focal date using a future value or present value calculation.
- If the payment is moving forward in time to get to the focal date, the payment is a present value and you need to find its future value at the focal date.
- If the payment is moving backward in time to get to the focal date, the payment is a future value and you need to find its present value at the focal date.
- The sum of the payments in the original payment stream at the focal date equals the sum of the payments in the new payment stream at the focal date. This creates an equation that allows you to solve for the unknown in the new payment stream.
EXAMPLE
You have three debts to the same creditor: $3,000 due today, $2,500 due in 2.25 years, and $4,250 due in 3 years 11 months. Unable to fulfill this obligation, you arrange with your creditor to make two alternative payments: $3,500 in nine months and a second payment due in two years. You agree upon an interest rate of 9.84% compounded monthly. What is the amount of the second payment?
Solution:
Step 1: Draw the timeline. With two payment streams and multiple amounts all on different dates, visualize two timelines, one for the original payment stream and the other for the new payment stream. Alternatively, draw one timeline with the payment streams in different colours. The unknown payment in the new payment stream is represented by [latex]x[/latex].

Step 2: Choose two years from today as the focal date.
Step 3: Calculate the future value of the $3,000 payment today (in the original payment stream) at the focal date. Because this payment must move forward in time to get to the focal date, the $3,000 is a present value and its value at the focal date is a future value. This payment must move 2 years (from today to 2 years from today) to get to the focal date, so the time for the future value calculation is 2 years.
| N | [latex]12 \times 2=24[/latex] |
| PV | [latex]-3,000[/latex] |
| FV | ? |
| PMT | [latex]0[/latex] |
| I/Y | [latex]9.84[/latex] |
| P/Y | [latex]12[/latex] |
| C/Y | [latex]12[/latex] |
[latex]\displaystyle{FV_1=\$3,649.57}[/latex]
Step 4: Calculate the present value of the $2,500 payment 2.25 years from today (in the original payment stream) at the focal date. Because this payment must move backward in time to get to the focal date, the $2,500 is a future value and its value at the focal date is a present value. This payment must move 0.25 years (from 2.25 years from today to 2 years from today) to get to the focal date, so the time for the present value calculation is 0.25 years.
| N | [latex]12 \times 0.25=3[/latex] |
| PV | ? |
| FV | [latex]-2,500[/latex] |
| PMT | [latex]0[/latex] |
| I/Y | [latex]9.84[/latex] |
| P/Y | [latex]12[/latex] |
| C/Y | [latex]12[/latex] |
[latex]\displaystyle{PV_1=\$2,439.49}[/latex]
Step 5: Calculate the present value of the $4,250 payment 3 years and 11 months from today (in the original payment stream) at the focal date. Because this payment must move backward in time to get to the focal date, the $4,250 is a future value and its value at the focal date is a present value. This payment must move 1 year, 11 months (from 3 years, 11 months from today to 2 years from today) to get to the focal date, so the time for the present value calculation is 1 year, 11 months.
| N | [latex]12 \times \frac{23}{12}=23[/latex] |
| PV | ? |
| FV | [latex]-4,250[/latex] |
| PMT | [latex]0[/latex] |
| I/Y | [latex]9.84[/latex] |
| P/Y | [latex]12[/latex] |
| C/Y | [latex]12[/latex] |
[latex]\displaystyle{PV_2=\$3,522.21}[/latex]
Step 6: Calculate the future value of the $3,500 payment 9 months from today (in the new payment stream) at the focal date. Because this payment must move forward in time to get to the focal date, the $3,500 is a present value and its value at the focal date is a future value. This payment must move 1 year, 3 months (from 9 months from today to 2 years from today) to get to the focal date, so the time for the future value calculation is 1 year, 3 months.
| N | [latex]12 \times \frac{15}{12}=15[/latex] |
| PV | [latex]-3,500[/latex] |
| FV | ? |
| PMT | [latex]0[/latex] |
| I/Y | [latex]9.84[/latex] |
| P/Y | [latex]12[/latex] |
| C/Y | [latex]12[/latex] |
[latex]\displaystyle{FV_2=\$3,956.11}[/latex]
Step 7: At the focal date, the sum of the payments in the original payment stream equal the sum of the payments in the new payment stream.
[latex]\begin{eqnarray*} 3,649.57+2,439.49+3,522.21 & = & 3,956.11+x \\ 9,611.27 & = & 3,956.11+x \\ 9,611.27-3,956.11 & = & x \\ \$5,644.16 & = & x \end{eqnarray*}[/latex]
The amount of the second payment is $5,644.16.
NOTE
It does not matter what focal date you choose because two values that are equal when moved to one date in common will still be equal when both are moved together to another date. But you should simplify your calculations by selecting a focal date corresponding to the date of an unknown variable. It is always easier to move actual amounts of money than it is to move an unknown variable [latex]x[/latex]. For example, in the previous question, suppose you selected today as the focal date (instead of 2 years). Then the [latex]x[/latex] at 2 years would need to be moved to today (the focal date). Regardless of the chosen focal date, the final answer will be the same.
TRY IT
Loan payments of $5,000 due two years ago and $3,000 due today have not been made. Instead, the payments are rescheduled with two payments of $1,500 in 1 year and 2.5 years, and a final payment in 4 years. What is the size of the final payment if money earns 3.7% compounded semi-annually?
Click to see Solution
Using 4 years as the focal date:
| N | [latex]12[/latex] | [latex]8[/latex] | [latex]6[/latex] | [latex]3[/latex] |
| PV | [latex]-5,000[/latex] | [latex]-3,000[/latex] | [latex]-1,500[/latex] | [latex]-1,500 [/latex] |
| FV | [latex]\textcolor{blue}{6,230.21}[/latex] | [latex]\textcolor{blue}{3,473.84}[/latex] | [latex]\textcolor{blue}{1,674.39}[/latex] | [latex]\textcolor{blue}{1,584.80}[/latex] |
| PMT | [latex]0[/latex] | [latex]0[/latex] | [latex]0[/latex] | [latex]0[/latex] |
| I/Y | [latex]3.7[/latex] | [latex]3.7[/latex] | [latex]3.7[/latex] | [latex]3.7[/latex] |
| P/Y | [latex]2[/latex] | [latex]2[/latex] | [latex]2[/latex] | [latex]2[/latex] |
| C/Y | [latex]2[/latex] | [latex]2[/latex] | [latex]2[/latex] | [latex]2[/latex] |
[latex]\begin{eqnarray*} 6,230.21+3,473.84 & = & 1,674.39+1,584.80+x \\ 9,704.05 & = & 3,259.19+x \\ 9,704.05-3,259.19 & = & x \\ \$6,444.86 & = & x \end{eqnarray*}[/latex]
EXAMPLE
A $10,000 loan is to be repaid with three equal payments made in 1 year, 3.5 years and 6 years. If money earns interest at 4.7% compounded quarterly, what is the size of the payments?
Solution:
Step 1: Draw the timeline. The $10,000 from the original payment stream is in black. The unknown payments in the new payments stream, represented by [latex]x[/latex], are in red.
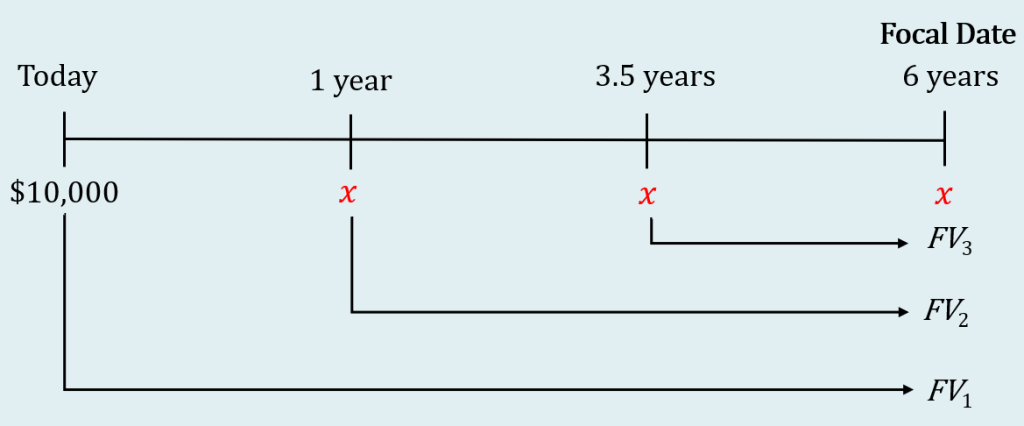
Step 2: Choose six years from today as the focal date.
Step 3: Calculate the future value of the $10,000 payment today (in the original payment stream) at the focal date. Because this payment must move forward in time to get to the focal date, the $10,000 is a present value and its value at the focal date is a future value. This payment must move 6 years (from today to 6 years from today) to get to the focal date, so the time for the future value calculation is 6 years.
| N | [latex]4 \times 6=24[/latex] |
| PV | [latex]-10,000[/latex] |
| FV | ? |
| PMT | [latex]0[/latex] |
| I/Y | [latex]4.7[/latex] |
| P/Y | [latex]4[/latex] |
| C/Y | [latex]4[/latex] |
[latex]\displaystyle{FV_1=\$13,236.01}[/latex]
Step 4: Calculate the future value of the [latex]x[/latex] at 1 year (in the new payment stream) at the focal date. Because this payment must move forward in time to get to the focal date, the [latex]x[/latex] is a present value and its value at the focal date is a future value. This payment must move 5 years (from 1 year from today to 6 years from today) to get to the focal date, so the time for the future value calculation is 5 years.
Because [latex]x[/latex] cannot be entered in the calculator, you need to find a expression for the future value of [latex]x[/latex] at the focal date. You can think of the unknown payment [latex]x[/latex] as [latex]1 \times x[/latex]. The future value of [latex]x[/latex] is the [latex]\mbox{(future value of 1)} \times x[/latex]. You can find the future value of 1 using the calculator by entering 1 for the present value and calculating out the future value.
| N | [latex]4 \times 5=20[/latex] |
| PV | [latex]-1[/latex] |
| FV | [latex]\textcolor{blue}{1.2631...}[/latex] |
| PMT | [latex]0[/latex] |
| I/Y | [latex]4.7[/latex] |
| P/Y | [latex]4[/latex] |
| C/Y | [latex]4[/latex] |
[latex]\displaystyle{FV_2=1.2631... \times x}[/latex]
Step 5: Calculate the future value of the [latex]x[/latex] at 3.5 year (in the new payment stream) at the focal date. Because this payment must move forward in time to get to the focal date, the [latex]x[/latex] is a present value and its value at the focal date is a future value. This payment must move 2.5 years (from 3.5 yeas from today to 6 years from today) to get to the focal date, so the time for the future value calculation is 2.5 years.
Because [latex]x[/latex] cannot be entered in the calculator, you need to find a expression for the future value of [latex]x[/latex] at the focal date. You can think of the unknown payment [latex]x[/latex] as [latex]1 \times x[/latex]. The future value of [latex]x[/latex] is the [latex]\mbox{(future value of 1)} \times x[/latex]. You can find the future value of 1 using the calculator by entering 1 for the present value and calculating out the future value.
| N | [latex]4 \times 2.5=10[/latex] |
| PV | [latex]-1[/latex] |
| FV | [latex]\textcolor{blue}{1.1239...}[/latex] |
| PMT | [latex]0[/latex] |
| I/Y | [latex]4.7[/latex] |
| P/Y | [latex]4[/latex] |
| C/Y | [latex]4[/latex] |
[latex]\displaystyle{FV_3=1.1239... \times x}[/latex]
Step 6: At the focal date, the sum of the payments in the original payment stream equal the sum of the payments in the new payment stream.
[latex]\begin{eqnarray*} 13,236.01 & = & x+(1.2631...) \times x+(1.1239...)\times x \\ 13,236.01 & = & (1+1.2631...+1.1239...) \times x \\ 13,236.01 & = & x \times 3.38708... \\ \frac{13,236.01}{3.38708...} & = & x \\ $3,907.78 & = & x \end{eqnarray*}[/latex]
The payments are $3,907.78.
NOTES
- You can choose any of the dates on the timeline in the previous example as the focal date. A different focal date will require different calculations to move the payments to the focal date, but the final answer will be the same.
- Keep all of the decimal places throughout the calculation, especially for the future or present value expressions for any unknown payments [latex]x[/latex], to avoid any round-off error in the final answer.
- To move an unknown payment [latex]x[/latex] to the focal date, find the value of 1 at the focal date and then multiply this value by [latex]x[/latex].
- If [latex]x[/latex] moves forward in time to get to the focal date, you need to find the future value of [latex]x[/latex]. To do this, find the future value of 1 and then the value of [latex]x[/latex] at the focal date is [latex](\mbox{future value of 1}) \times x[/latex].
- If [latex]x[/latex] moves backward in time to get to the focal date, you need to find the present value of [latex]x[/latex]. To do this, find the present value of 1 and then the value of [latex]x[/latex] at the focal date is [latex](\mbox{present value of 1}) \times x[/latex].
TRY IT
Payments of $570 due 1.5 years ago and $890 due 6 months ago have not been made. Instead, these payments are to be replaced with two equal payments due 9 months and 2 years from today. If money earns 5% compounded monthly, what is the size of the payments?
Click to see Solution
Using 2 years from today as the focal date:
| N | [latex]42[/latex] | [latex]30[/latex] | [latex]15[/latex] |
| PV | [latex]-5,70[/latex] | [latex]-890[/latex] | [latex]-1[/latex] |
| FV | [latex]\textcolor{blue}{678.76}[/latex] | [latex]\textcolor{blue}{1,008.24}[/latex] | [latex]\textcolor{blue}{1.06435...}[/latex] |
| PMT | [latex]0[/latex] | [latex]0[/latex] | [latex]0[/latex] |
| I/Y | [latex]5[/latex] | [latex]5[/latex] | [latex]5[/latex] |
| P/Y | [latex]12[/latex] | [latex]12[/latex] | [latex]12[/latex] |
| C/Y | [latex]12[/latex] | [latex]12[/latex] | [latex]12[/latex] |
[latex]\begin{eqnarray*} 678.76+1,008.24 & = & x +(1.06435...) \times x \\ 1,678 & = & (1+1.06435...) \times x \\ 1,678 & = & (2.06435...) \times x \\ \frac{1,678}{2.06435...} & = & x \\ \$817.21 & = & x \end{eqnarray*}[/latex]
Exercises
- If money earns 6% compounded monthly, what single payment due in 27 months is equivalent to payments of $5,000 today and $5,000 in three years?
Click to see Answer
$10,501.28
- If money earns 8.5% compounded quarterly, what single payment due in 2 years is equivalent to payments of $4,385 due 1 year ago and $6,000 due in 4 years?
Click to see Answer
$10,714.59
- If money earns 6.65% compounded monthly, what single payment due in 16 months is equivalent to payments of $16,000 due today, $8,000 due in 10 months, and $19,000 due in 33 months?
Click to see Answer
$43,045.16
- A $35,000 loan taken out today is to be repaid with a $15,000 payment due in 6 months and a second unknown payment due in 2 years. If money earns 5.95% compounded semi-annually, find the size of the unknown payment due in 2 years.
Click to see Answer
$22,975.60
- A $51,000 loan borrowed a today is to be repaid with a $15,000 payment due in 3 months, a $10,000 payment due in 1 year, and an unknown payment due in 1.5 years. If money earns 6.32% compounded quarterly, what is the size of the unknown payment?
Click to see Answer
$29,488.31
- A $44,000 loan borrowed today is repaid with two equal payments due in 6 months and 15 months. If money earns 5.55% compounded monthly, what is the size of the payments.
Click to see Answer
$23,087.18
- If money earns 8.88% compounded monthly, what two equal payments, one due today and one due in 18 months would be equivalent to two equal payments of $2,500, one due 1 year ago and one due in 6 months?
Click to see Answer
$2,731.26
- Payments of $38,000 due 1.5 years ago, $17,000 due 6 months ago and $45,000 due in 1 year are replaced with three equal payments due today, in 18 months and in 2 years. If money earns 9.5% compounded semi-annually, find the size of the payments.
Click to see Answer
$37,952.43
- Payments of $3,750 due 2.5 years ago, $2,400 due in 3.25 years and $1,950 in 5 years are replaced with three equal payments due in 1 year, 2 years and 4.5 years. If money earns 10.75% compounded quarterly, find the size of the payments.
Click to see Answer
$3,322.29
- A winning lottery ticket offers the following two options:
- Option A: A single payment of $1,000,000 today.
- Option B: $250,000 today followed by annual payments of $300,000 for the next three years.
If money can earn 9% compounded annually, which option should the winner select? How much better is that option in
current dollars?Click to see Answer
Option B by $9,388.40
- Darwin is a young entrepreneur trying to keep his business afloat. He has missed two payments to a creditor. The first was for $3,485 seven months ago and the second was for $5,320 last month. Darwin has had discussions with his creditor, who is willing to accept $4,000 one month from now and a second payment in full six months from now. If the agreed upon interest rate is 7.35% compounded monthly, what is the amount of the second payment?
Click to see Answer
$5,201.24
- James is a debt collector. One of his clients has asked him to collect an outstanding debt from one of its customers. The customer has failed to pay three amounts: $1,600 18 months ago, $2,300 nine months ago, and $5,100 three months ago. In discussions with the customer, James finds she desires to clear up this situation and proposes a payment of $1,000 today, $4,000 nine months from now, and a final payment two years from now. The client normally charges 16.5% compounded quarterly on all outstanding debts. What is the amount of the third payment?
Click to see Answer
$7,465.59
- Working in the accounting department, Ariel has noticed that a customer is having trouble paying its bills. The customer has missed a payment of $2,980 two years ago, $5,150 14 months ago, and $4,140 four months ago. The customer proposes making two equal payments in six months and in 18 months. If the agreed-upon interest rate is 6.89% compounded monthly, what are the amounts of each payment?
Click to see Answer
$7,083.74
- A $30,000 loan at 4.9% compounded semi-annually is to be repaid with four equal semi-annual payments. The first payment is one year after the loan. Calculate the amount of each payment.
Click to see Answer
$8,160.07
- The Ontario Labour Relations Board is reviewing a human resource complaint. At the time of filing, a construction worker indicated that her employer failed to pay her monthly wages of $3,400, $3,200, $3,600, and $3,475 starting four months prior. It has taken the Ontario Labour Relations Board nine months since the time of filing to gather the needed information and make a judgment in favour of the complainant. If the standard interest rate used in its judgment is 9% compounded monthly, what amount is awarded to the construction worker?
Click to see Answer
$14,900.01
- Larry is a financial adviser helping a client save up $100,000 in five years’ time. The client has the financial means to pursue either of the following two alternatives:
- Option A: Make three equal deposits due today, in 2 years, and 4 years.
- Option B: Make four equal deposits due today, in 1 year, in 3 years, and 4½ years.
If Larry can invest the funds at 9% compounded semi-annually, which option is in the best interests of the client? In current dollars, how much better for the client is that recommended option?
Click to see Answer
Option A by $735.14
- Yi-Fang is the store owner of a franchise. In flipping through her records, she notices the following debts to the same supplier: $2,389.56 due eight months ago, $3,478.34 due six months ago, $1,694.32 due four months ago, $6,497.98 due two months ago, $4,611.03 due today, $5,784.39 due in two months, and $5,177.44 due in four months. She would like to clear all of these debts with a single payment next month. If the supplier charges 18.1% compounded monthly on overdue balances and provides a credit of 9% compounded monthly on early payments, calculate the amount of the payment.
Click to see Answer
$30,703.92
Attribution
“9.4: Equivalent Payments” from Business Math: A Step-by-Step Handbook Abridged by Sanja Krajisnik; Carol Leppinen; and Jelena Loncar-Vines is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.
“9.4: Equivalent Payments” from Business Math: A Step-by-Step Handbook (2021B) by J. Olivier and Lyryx Learning Inc. through a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License unless otherwise noted.

