5.8 Perpetuities
LEARNING OBJECTIVES
- Solve problems involving a perpetuity.
Some of the scholarships offered to students at your college were created decades ago, yet these scholarships continue to pay out money to students each and every year. Where does all of the money come from? Did somebody bestow a tremendously large endowment fund all those many years ago to sustain the scholarship over decades? Or does an individual or supporting organization simply pay it out of pocket each year? How is it possible for these scholarships to pay out through all the past years and all of the foreseeable years?
Scholarships, like the one described above, are examples of perpetuities, which are annuities that have an infinite term. In other words, the payments last forever. At your individual level, any sum of money you invest as a perpetuity can be used to generate income forever. At the professional level, many companies and not-for-profit organizations such as sports clubs establish scholarship programs and bursaries for their employees, members, or clients. In some contracts, payments such as royalties continue forever. Some divided stocks have their price determined by indefinite future dividend amounts.
What are Perpetuities?
A perpetuity is a special type of annuity that has fixed, regular payments that continue indefinitely. If the principal of the investment is never withdrawn, then the interest earned each period can be withdrawn without affecting the future interest earnings of the investment. Therefore, the annuity continues to earn the same amount of interest each and every future interval and can pay out interest forever.
A perpetuity can be an ordinary perpetuity or a perpetuity due. As well, the payment frequency and compounding frequency create either a simple or general annuity structure. Perpetuities can even occur after a deferral period, and hence deferred perpetuities are possible.
The Perpetuity Formulas
The present value for an ordinary perpetuity is
[latex]\displaystyle{PV=\frac{PMT}{i_2}}[/latex]
and the present value for a perpetuity due is
[latex]\displaystyle{PV=(1+i_2) \times \frac{PMT}{i_2}}[/latex]
where
- [latex]PV[/latex] is the present value of the perpetuity. The present value is the sum of the present value of all of the annuity payments at the start of the first payment interval.
- [latex]PMT[/latex] is the annuity payment. The amount of money that is invested or paid after each payment interval.
- [latex]i_2[/latex] is the periodic interest rate for the interest rate whose compounding frequency matches the payment frequency. If the annuity is a simple annuity, the compounding frequency and the payment frequency are equal and the given interest rate can be used to calculate the periodic interest rate. If the annuity is a general annuity, the compounding frequency and the payment frequency are different and an interest conversion must be done first to find the equivalent interest rate with the compounding frequency equal to the payment frequency.
NOTES
- There is no future value formula for a perpetuity. Because a perpetuity lasts forever, the future value is an undefined quantity.
- There is no N value in perpetuity formulas. Because a perpetuity lasts forever, the term of a perpetuity is an undefined quantity.
- For perpetuity questions, there are only three possible quantities to solve for: PV, PMT or I/Y.
- In a simple perpetuity, the payment frequency and the compounding frequency are equal (P/Y=C/Y). In this situation the periodic interest rate [latex]i_2=\frac{j}{m}[/latex] where [latex]j[/latex] is the nominal interest rate given in the question and [latex]m[/latex] is the compounding frequency (and the payment frequency).
- In a general perpetuity, the payment frequency and the compounding frequency are not equal (P/Y ≠ C/Y). In this situation, the given interest rate must first be converted to the equivalent interest rate where the new compounding frequency equals the payment frequency. Using the equivalent interest rate, calculate the periodic interest rate [latex]i_2[/latex].
The steps required to solve for the present value or payment of a perpetuity remain essentially unchanged from solving for the present value or payment of any annuity.
EXAMPLE
Your college wants to provide a $2,000 scholarship at the end of every quarter. How much money does the college need to invest today at 4% compounded quarterly to sustain this scholarship indefinitely?
Solution:
Step 1: The payments are at the beginning of the payment intervals, and both the compounding frequency and the payment frequency are the same (both quarterly). This is a ordinary simple perpetuity. Because this is a simple perpetuity, an interest rate conversion is not required.
The given information is
[latex]\begin{eqnarray*} PMT & = & \$2,000 \\ P/Y & = & 4 \\ I/Y & = & 4\% \\ C/Y & = & 4 \end{eqnarray*}[/latex]
Step 2: Calculate the periodic interest rate.
[latex]\begin{eqnarray*} i_2 & = & \frac{I/Y}{C/Y} \\ & = & \frac{4\%}{4}\\ & = & 1\%\end{eqnarray*}[/latex]
Step 3: Calculate the present value.
[latex]\begin{eqnarray*} PV & = & \frac{PMT}{i_2} \\ & = & \frac{2,000}{0.01} \\ & = & \$200,000 \end{eqnarray*}[/latex]
The college needs to invest $200,000 today to sustain the scholarship indefinitely.
NOTE
In the previous example, the $2,000 payments from the perpetuity come from the interest generated by the $200,000 investment. At 4% compounded quarterly, $2,000 in interest is accumulated at the end of each quarter. The $2,000 in interest becomes the payment. None of the $200,000 principal is ever used to make up the payment. Consequently, the $2,000 payments will last forever.
Using a Financial Calculator
The TI BAII Plus calculator is set up for fixed term annuities only. That is, the calculator can only deal with annuities that have a definite end date. Therefore, the calculator has no specific built-in function or manner in which to handle a perpetuity. However, because a perpetuity is a specialized version of a regular annuity, a few minor adaptations to the annuity inputs will allow you to trick the calculator into calculating answers for perpetuities.
USING THE TI BAII PLUS CALCULATOR ON PERPETUITIES
- Set the calculator to the correct payment setting (END or BGN).
- Set FV to 0.
- Set N to 10,000.
- Enter the values for the other known variables as normal.
- After all of the known quantities are loaded into the calculator, calculate the unknown quantity (PV, PMT or I/Y depending on the question.)
NOTES
- The future value of a perpetuity is undefined. But you must enter something into the calculator for FV. The convention is to set FV to 0. This will not affect the perpetuity calculation.
- Setting N to 10,000 will trick the calculator into generating the answer to a perpetuity question. A large value of N places the future value far into the distance future, creating an annuity that lasts a very, very long time. There is nothing special about 10,000, except that it is a very large number. Any very large number for N will work, but it has to be a large enough number to get the calculator to solve the perpetuity question. Using 10,000 is a large enough number to solve the perpetuity question but not so large that it exceeds the computational abilities of the calculator (i.e. sending the calculator into an indefinite loop or producing an error). If you experience an error, try lowering the value of N a little bit. However, try to avoid using a number less than 10,000 if possible to ensure that the calculator finds the answer to the perpetuity question, and not just a fixed term annuity that lasts a long time.
- Ensure that the calculator is set to the required payment setting. As with any annuity, the answer for a perpetuity will be different for payments at the end or beginning of the interval.
- Because you can enter P/Y and C/Y, there is no need to do an interest conversion for a general perpetuity. You simply have to tell the calculator the P/Y and C/Y given in the question, and the calculator will handle any interest conversion internally.
- The values you enter for PV and PMT must adhere to the cash flow sign convention.
EXAMPLE
In memory of his late father, who was a highly successful marketing manager, Brian would like to set up a marketing scholarship program with his university’s school of business. He is able to donate $100,000 from his father’s estate to set up the fund. If the perpetuity fund can earn 6.3% compounded semi-annually and the first scholarship is to be provided immediately, what semi-annual scholarship amount can the fund offer?
Solution:
| PMT Setting | BGN |
| N | [latex]10,000[/latex] |
| PV | [latex]-100,000[/latex] |
| FV | [latex]0[/latex] |
| PMT | ? |
| I/Y | [latex]6.3[/latex] |
| P/Y | [latex]2[/latex] |
| C/Y | [latex]2[/latex] |
[latex]PMT=\$3,053.81[/latex]
The fund can provide semi-annual scholarships for $3,053.81.
EXAMPLE
One of the methods for valuing common shares is to determine the present value of its future dividends. If IBM Corporation is forecast to have year-end dividends of $1.50 per share in perpetuity, how much should an investor be willing to pay for a share if he requires a 12% compounded quarterly rate of return?
Solution:
| PMT Setting | END |
| N | [latex]10,000[/latex] |
| PV | ? |
| FV | [latex]0[/latex] |
| PMT | [latex]1.50[/latex] |
| I/Y | [latex]12[/latex] |
| P/Y | [latex]1[/latex] |
| C/Y | [latex]4[/latex] |
[latex]PV=\$11.95[/latex]
An investor should pay $11.95 per share.
EXAMPLE
A college invests $500,000 in an endowment fund to provide month-end scholarships of $800. What interest rate compounded semi-annually does the fund need to earn to provide the scholarships indefinitely?
Solution:
| PMT Setting | END |
| N | [latex]10,000[/latex] |
| PV | [latex]-500,000[/latex] |
| FV | [latex]0[/latex] |
| PMT | [latex]800[/latex] |
| I/Y | ? |
| P/Y | [latex]12[/latex] |
| C/Y | [latex]2[/latex] |
[latex]I/Y=1.44%[/latex]
The fund must earn 1.44% compounded semi-annually.
TRY IT
What amount do you need to invest today at 2.9% compounded quarterly to sustain payments of $450 at the end of every month indefinitely?
Click to see Solution
| PMT Setting | END |
| N | [latex]10,000[/latex] |
| PV | ? |
| FV | [latex]0[/latex] |
| PMT | [latex]450[/latex] |
| I/Y | [latex]2.9[/latex] |
| P/Y | [latex]12[/latex] |
| C/Y | [latex]4[/latex] |
[latex]PV=\$186,656.17[/latex]
TRY IT
You invest $150,000 today into a investment earning 3.72% compounded monthly. You want to receive beginning-of quarter payments in perpetuity. Calculate the size of the payments.
Click to see Solution
| PMT Setting | BGN |
| N | [latex]10,000[/latex] |
| PV | [latex]-150,000[/latex] |
| FV | [latex]0[/latex] |
| PMT | ? |
| I/Y | [latex]3.72[/latex] |
| P/Y | [latex]4[/latex] |
| C/Y | [latex]12[/latex] |
[latex]PMT=\$1,386.40[/latex]
TRY IT
An investor purchased shares in a business when the market price per share was $100. Each share pays quarterly dividends of $2.50. What effective rate of return does the investor realize on her investment?
Click to see Solution
| PMT Setting | END |
| N | [latex]10,000[/latex] |
| PV | [latex]-100[/latex] |
| FV | [latex]0[/latex] |
| PMT | [latex]2.50[/latex] |
| I/Y | ? |
| P/Y | [latex]4[/latex] |
| C/Y | [latex]1[/latex] |
[latex]I/Y=10.38\%[/latex]
EXAMPLE
You purchase an investment that will pay you $1,500 every quarter in perpetuity. You will receive your first payment in seven years. If the perpetuity earns 2.3% compounded semi-annually, what is the purchase price of the investment?
Solution:
Step 1: Draw the timeline for the deferred perpetuity. Treat the perpetuity as a perpetuity due with the payments at the beginning of the interval.
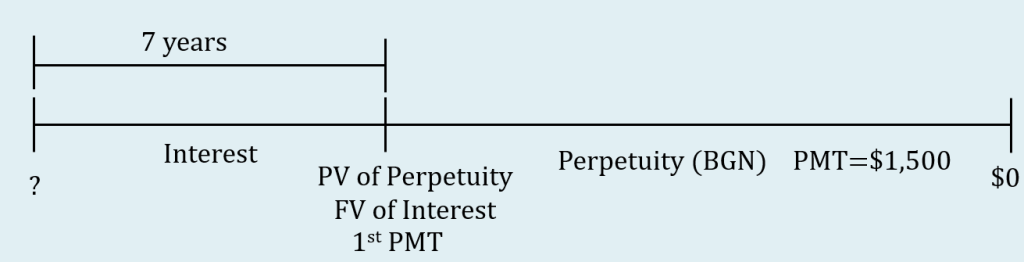
Some notes about the timeline.
- The present value at the start of the interest period is unknown.
- Because the payments are at the beginning of the payment interval, the present value of the perpetuity and the first payment occur at the same time, at the start of the annuity. There is a 7 year gap from the start of the interest period and the present value of annuity/future value of interest/first payment.
- The $1,500 payments for the perpetuity last indefinitely.
- The present value of the perpetuity becomes the future value of the interest period. Then, the future value of the interest period will be moved back 7 years to the start of the interest period.
Step 2: Calculate the present value of the perpetuity.
| PMT Setting | BGN |
| N | [latex]10,000[/latex] |
| PV | ? |
| FV | [latex]0[/latex] |
| PMT | [latex]1,500[/latex] |
| I/Y | [latex]2.3[/latex] |
| P/Y | [latex]4[/latex] |
| C/Y | [latex]2[/latex] |
[latex]PV=\$263,117.421...[/latex]
Step 3: Calculate the present value for the interest period. The present value calculated in the previous step becomes the future value for the interest period: [latex]FV=\$263,117.421...[/latex]
| N | [latex]2 \times 7=14[/latex] |
| PV | ? |
| FV | [latex]263,117.421...[/latex] |
| PMT | [latex]0[/latex] |
| I/Y | [latex]2.3[/latex] |
| P/Y | [latex]2[/latex] |
| C/Y | [latex]2[/latex] |
[latex]PV=\$224,195.65[/latex]
The purchase price of the investment is $224,195.65.
TRY IT
A college invests $500,000 today in an endowment fund to provide semi-annual scholarships in perpetuity. The first scholarship will be given out 10 years from now. If the endowment fund earns 3.9% compounded monthly, what is the scholarship amount?
Click to see Solution
| PMT Setting | BGN | |
| N | [latex]120[/latex] | [latex]10,000[/latex] |
| PV | [latex]-500,000[/latex] | [latex]-738,023.537...[/latex] |
| FV | [latex]\textcolor{blue}{738,023.537...}[/latex] | [latex]0[/latex] |
| PMT | [latex]0[/latex] | [latex]\textcolor{blue}{14,229.16}[/latex] |
| I/Y | [latex]3.9[/latex] | [latex]3.9[/latex] |
| P/Y | [latex]12[/latex] | [latex]2[/latex] |
| C/Y | [latex]12[/latex] | [latex]12[/latex] |
[latex]\displaystyle{PMT=\$14,229.16}[/latex]
Exercises
- How much money must be invested today to sustain beginning-of-six month payments of $20,000 in perpetuity at 8.4% compounded semi-annually?
Click to see Answer
$496,190.48
- What quarterly payments in perpetuity can be received if $2,400,000 is invested at 4.4% compounded quarterly?
Click to see Answer
$26,400
- You want to receive $10,000 every six months in perpetuity from an investment. How much money do you need to invest if the money earns 5.35% compounded quarterly?
Click to see Answer
$371,349.38
- You invest $500,000 today in an investment at 5.5% compounded annually. What payment can you receive every six months in perpetuity if the first payment is received today?
Click to see Answer
$13,207.62
- How much money is required today to fund a perpetuity earning 5.65% annually that needs to pay out $17,000 at the end of each year?
Click to see Answer
$300,884.96
- If $2,500,000 was invested at 4.8% compounded semi-annually, what payment at the end of every six months could be sustained in perpetuity?
Click to see Answer
$60,000
- The dean of the School of Business and Applied Arts at Red River College in Winnipeg wants to establish a scholarship program for the newly created finance major in its business administration stream. He wants to distribute five $2,000 scholarships annually starting immediately. How much money must he raise from college supporters if the perpetuity can earn 3.6% compounded monthly?
Click to see Answer
$283,224.19
- Samson just won the grand prize of $50 million in the Lotto Max lottery. If he invests the money into a perpetuity fund earning 5.5% compounded annually, what monthly payment can he expect to receive starting today?
Click to see Answer
$222,589.59
- An investor states that he would be willing to pay $25 for common shares to achieve his desired rate of return of 15% annually. What are the forecasted annual dividends starting one year from now?
Click to see Answer
$3.75
- The Coca-Cola Company is forecasted to have dividends of $0.50 per share quarterly for the next five years, followed by dividends of $0.70 per share quarterly in perpetuity. If an investor desires a 10% compounded annually rate of return, what amount would she be willing to pay per share?
Click to see Answer
$25.89
- Indigo’s will states that $150,000 is to be set aside into a fund that will make annual payments to her grandson starting when he turns 18 years old. If Indigo dies when her grandson is six years old and the fund can earn 4.9% compounded quarterly, what annual payment will he receive in perpetuity?
Click to see Answer
$12,791.51
- In 2009, the Canadian federal government committed $1.5 million in annual operating funding for the Canadian Museum for Human Rights in Winnipeg, which opened in 2014. If the government had funded the museum by setting up an ordinary perpetuity in 2009 that could earn prevailing interest rates of 3% compounded annually, how much money would have been required?
Click to see Answer
$45,757,082.97
Attribution
“12.3: Perpetuities” from Business Math: A Step-by-Step Handbook (2021B) by J. Olivier and Lyryx Learning Inc. through a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License unless otherwise noted.

