Il ne suffit pas de s’assurer qu’un projet est réalisé dans les délais et dans le respect du budget. Vous devez vous assurer de fabriquer le bon produit pour répondre aux besoins de vos intervenants. La qualité, c’est s’assurer de construire ce qui est prévu et de le faire de la manière la plus efficace possible. Cela signifie qu’il faut essayer de limiter les erreurs et veiller à ce que votre projet tende toujours vers votre objectif, qui est de créer le bon produit.
Tout le monde « sait » ce qu’est la qualité. Toutefois, la façon dont on utilise ce mot dans la vie de tous les jours est un peu différente de la façon dont il est utilisé en gestion de projet. Tout comme la triple contrainte (portée, coût et calendrier), vous gérez la qualité d’un projet en fixant des objectifs et en prenant des mesures. C’est pourquoi vous devez comprendre les niveaux de qualité que vos intervenants jugent acceptables et veiller à ce que votre projet atteigne ces objectifs, tout comme il doit atteindre leurs objectifs en matière de budget et de calendrier.
Satisfaire le client consiste à s’assurer que les personnes qui paient pour le produit final sont satisfaites de ce qu’elles obtiennent. Au moment de recueillir les exigences de spécifications, l’équipe tente d’écrire toutes les choses que les clients veulent par rapport à leur produit afin que de savoir comment les satisfaire. Certaines exigences peuvent ne pas être formulées. Ce sont celles qui sont tributaires des besoins explicites du client. Par exemple, certaines exigences relèvent du simple bon sens (p. ex., un produit que les gens tiennent dans leurs mains ne peut pas être fabriqué à partir de produits chimiques toxiques susceptibles de les tuer). Ce n’est peut-être pas explicite, mais c’est certainement une exigence.
Créer un produit « propre à l’emploi » consiste à s’assurer que le produit que vous créez est conçu de la meilleure façon pour répondre aux besoins du client. Quel serait votre choix : un produit magnifiquement conçu, bien construit, solide et totalement agréable à regarder, mais qui ne répond pas à vos besoins; ou un produit qui répond à vos attentes bien qu’il soit laid et difficile à utiliser? Vous choisirez toujours le produit qui correspond à vos besoins, même s’il est très limité. C’est pourquoi il est important que le produit fasse ce qu’il est censé faire et qu’il le fasse bien. Par exemple, vous pouvez planter un clou à l’aide d’un tournevis, mais un marteau convient mieux pour ce travail.
La conformité aux exigences est au cœur de la satisfaction du client et de l’obtention d’un produit propre à l’emploi, et permet de mesurer à quel point votre produit répond à vos attentes. Avant tout, votre produit doit faire ce que vous avez écrit dans votre énoncé des exigences. Vos exigences doivent tenir compte de ce qui satisfera votre client et de la meilleure conception possible pour le travail à effectuer. Cela signifie qu’il faut se conformer aux exigences déclarées et implicites.
En fin de compte, la qualité de votre produit est jugée par le fait que vous avez construit ce que vous aviez dit que vous construiriez.
L’élaboration du plan qualité consiste à prendre tous les renseignements disponibles au début du projet et à déterminer comment vous allez mesurer la qualité et prévenir les défectuosités. Votre entreprise doit disposer d’une politique qualité qui indique comment elle mesure la qualité dans l’ensemble de l’organisation. Vous devez vous assurer que votre projet respecte la politique de l’entreprise et toute règle ou réglementation gouvernementale sur la manière d’établir un plan qualité de votre projet.
Vous devez planifier les activités qui vous serviront à mesurer la qualité du produit du projet. Vous devrez également réfléchir au coût de toutes les activités liées à la qualité que vous souhaitez entreprendre. Ensuite, vous devrez définir des lignes directrices en matière de critères d’évaluation. Enfin, vous devrez concevoir les tests à réaliser lorsque le produit sera prêt à être mis à l’essai.
Qualité et classement
Selon l’Organisation internationale de normalisation (ISO), la qualité est « le degré auquel un ensemble de caractéristiques inhérentes répond aux exigences ». Les exigences d’un produit ou d’un processus peuvent être classées par catégories ou recevoir une note qui fournira une base de comparaison. La qualité est déterminée par une mesure permettant de définir si un produit répond bien aux exigences de sa catégorie.
Pour la plupart des gens, le terme de qualité fait aussi référence à un bon rapport qualité-prix; on en a pour son argent. Par exemple, même les produits de qualité inférieure doivent fonctionner comme prévu, être sécuritaires et durer un temps raisonnable. Prenons les exemples suivants.
Exemple : Qualité de l’essence
Les raffineurs de pétrole fournissent de l’essence en plusieurs qualités différentes en fonction de l’indice d’octane, car les indices d’octane plus élevés conviennent aux moteurs à plus forte compression. L’essence ne doit pas être contaminée par de la saleté ou de l’eau, et la performance réelle du carburant doit être proche de son indice d’octane. Une cargaison d’essence avec un faible indice d’octane de 87, exempte d’eau ou d’autres contaminants, serait de haute qualité, tandis qu’une cargaison d’essence à 93 d’indice d’octane qui est contaminée par des saletés serait de basse qualité.
Exemple : Qualité d’emballage des meubles
Jean possède des meubles anciens en excellent état qui lui ont été légués par sa grand-mère. Ces meubles ont une valeur sentimentale pour Jean, en plus d’avoir une valeur monétaire. Jean décide d’embaucher des déménageurs (des professionnels de haut niveau) pour charger ses meubles dans le camion en utilisant des rembourrages et des dispositifs de retenue appropriés afin d’éviter les bosses et les rayures pendant le déménagement. La norme de qualité de Jean est qu’aucun dommage observable ne soit causé à ses gros meubles, en particulier les antiquités. Si le mobilier arrive dans son nouvel appartement sans une seule bosse ou rayure ni autre dommage, l’activité sera de haute qualité. La norme de Jean pour l’emballage de sa cuisine est plus basse. Sa vaisselle étant vieille et bon marché, il décide de faire confiance à ses amis inexpérimentés (des amateurs de bas étage) pour l’aider à emballer le tout. Si quelques pièces de vaisselle ou de verrerie sont ébréchées ou cassées au cours du processus, l’économie réalisée sur les coûts de main-d’œuvre compensera largement la perte et aura une bonne valeur.
Statistiques
Pour évaluer la conformité des produits par rapport aux exigences de qualité, il suffit de prendre des mesures et de les interpréter. Les statistiques (l’interprétation mathématique des données numériques) sont utiles pour interpréter un grand nombre de mesures et servent à déterminer dans quelle mesure le produit respecte sa spécification même lorsqu’il est fabriqué de manière répétée. Les mesures effectuées sur des échantillons du produit doivent se situer à l’intérieur des limites de contrôle (les extrêmes supérieurs et inférieurs de la variation admissible), et il incombe à la direction de concevoir un processus qui produira régulièrement des produits se situant entre ces limites.
Les concepteurs pédagogiques utilisent souvent des statistiques pour déterminer la qualité de conception de leurs cours. Évaluer les étudiants permet aux concepteurs pédagogiques de savoir si l’apprentissage se déroule dans les limites de contrôle.
Exemple : Établir des limites de contrôle
Une raffinerie de pétrole produit de grandes quantités de carburant de différentes qualités. Des échantillons de carburant sont prélevés et mesurés à intervalles réguliers. Si un carburant est censé avoir un indice d’octane de 87, des échantillons de ce carburant devraient produire des résultats proches de cette valeur. Cependant, de nombreux échantillons auront des résultats différents de 87. Les différences sont dues à des facteurs aléatoires qu’il est difficile ou coûteux de contrôler. La plupart des échantillons doivent être proches du résultat de 87 et aucun ne doit en être trop éloigné. Le fabricant propose des qualités de 85 et 89, et décide donc qu’aucun des échantillons de carburant à 87 d’indice d’octane ne doit être inférieur à 86 ou supérieur à 88.
Si un processus est conçu pour fabriquer un produit d’une certaine taille ou d’une autre caractéristique mesurée, il est impossible de contrôler tous les petits facteurs qui peuvent faire en sorte que le produit diffère légèrement de la mesure souhaitée. Certains de ces facteurs donneront des produits dont les mesures seront plus grandes que souhaité, tandis que d’autres auront l’effet inverse. Si plusieurs facteurs aléatoires ont une incidence sur le processus, ils ont tendance à se compenser et les résultats les plus fréquents se situent vers le milieu de la fourchette; ce phénomène se nomme le théorème de la limite centrale.
Si l’éventail des valeurs de mesures possibles est divisé de manière égale en subdivisions appelées compartiments, les mesures peuvent être triées et le nombre de mesures qui tombent dans chaque compartiment peut être compté. Le résultat est une distribution de fréquences qui indique combien de mesures se trouvent dans chaque compartiment. Si les effets à l’origine des différences sont aléatoires et tendent à se compenser, la distribution de fréquences se nomme la distribution normale.
Si l’éventail des valeurs de mesures possibles est divisé de manière égale en subdivisions appelées compartiments, les mesures peuvent être triées et le nombre de mesures qui tombent dans chaque compartiment peut être compté. Le résultat est une distribution de fréquences qui indique combien de mesures se trouvent dans chaque compartiment. Si les effets à l’origine des différences sont aléatoires et tendent à se compenser, la distribution de fréquences est appelée la distribution normale, laquelle prend la forme d’une cloche dont les bords s’évasent. Les bords d’une courbe de distribution normale théorique sont très proches de zéro, mais ne l’atteignent pas.
b>, qui prend la forme d’une cloche dont les bords s’évasent. Les bords d’une courbe de distribution normale théorique sont très proches de zéro, mais ne l’atteignent pas.
Exemple : Distribution normale
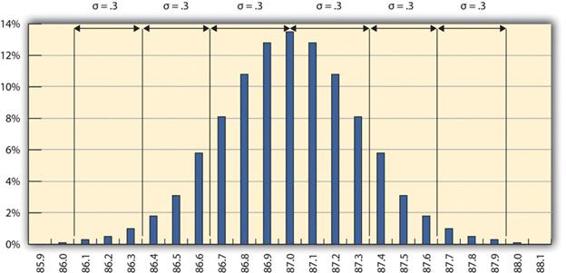
La responsable du contrôle de la qualité d’une raffinerie mesure de nombreux échantillons d’essence à 87 d’indice d’octane, classe les mesures en fonction de leur indice d’octane dans des compartiments d’une largeur de 0,1 d’indice d’octane, puis compte le nombre de mesures dans chaque compartiment. Elle crée ensuite un diagramme de distribution de fréquences des données, comme le montre la figure 14.1.
Il est fréquent de prélever des échantillons, c’est-à-dire des sous-ensembles de la population totale sélectionnés au hasard, et de mesurer et de comparer leurs qualités, car il serait fastidieux, voire impossible, de mesurer l’ensemble de la population. Si les mesures de l’échantillon sont réparties de manière égale au-dessus et au-dessous de la distribution centrale, comme c’est le cas dans la figure 14.1, la moyenne de ces mesures est également la valeur centrale, appelée moyenne et représentée dans les formules par la lettre grecque minuscule « µ » (prononcée mu). La différence entre les mesures et la valeur centrale s’appelle l’écart-type de l’échantillon ou simplement l’écart-type.
La première étape du calcul de l’écart-type consiste à soustraire chaque mesure de la valeur centrale (moyenne) et à élever cette différence au carré. (Rappel de vos cours de mathématiques : élever un nombre au carré revient à le multiplier par lui-même et le résultat est toujours positif.) L’étape suivante consiste à additionner ces valeurs au carré et à les diviser par le nombre de valeurs moins un. La dernière étape consiste à prendre la racine carrée. Le résultat peut être considéré comme une différence moyenne. (Si vous aviez utilisé la méthode habituelle de calcul de la moyenne, la somme des nombres positifs et négatifs aurait été égale à zéro.) Les mathématiciens représentent l’écart-type par la lettre grecque minuscule « σ » (prononcée sigma). Lorsque tous les éléments d’un groupe sont mesurés, et non un simple échantillon, on parle d’écart-type de la population et, dans un deuxième temps, la somme des valeurs au carré est divisée par le nombre total de valeurs.

Source : http://pm4id.org/10/1/
La figure 14.1 montre que les mesures les plus fréquentes d’indice d’octane sont proches de 87 et que les autres mesures sont réparties de manière égale au-dessus et au-dessous de 87. La forme du diagramme de distribution confirme l’hypothèse du théorème de la limite centrale selon laquelle les facteurs qui influencent l’indice d’octane sont aléatoires et tendent à se compenser, ce qui est indiqué par la forme symétrique. Cette distribution est un exemple classique de distribution normale. La responsable du contrôle de la qualité remarque qu’aucune des mesures n’est supérieure à 88 ou inférieure à 86 et qu’elles se situent donc dans les limites de contrôle, ce qui lui permet de conclure que le processus fonctionne de manière satisfaisante.
Exemple : Écart-type des échantillons d’essence
La responsable du contrôle de la qualité de la raffinerie utilise la fonction d’écart-type de son tableur pour déterminer l’écart-type des mesures de l’échantillon et constate que, pour ses données, l’écart-type est de 0,3 d’indice d’octane. Elle marque l’intervalle sur le diagramme de distribution de fréquences pour montrer les valeurs qui se situent à un sigma (écart-type) de chaque côté de la moyenne (figure 14.2).
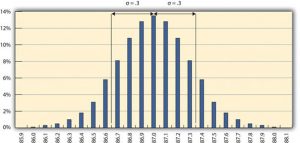
La plupart des mesures se situent à 0,3 d’indice d’octane près par rapport à 87.
Source : http://pm4id.org/10/1/
Pour les distributions normales, environ 68,3 % des mesures se situent à moins d’un écart-type de part et d’autre de la moyenne. Il s’agit d’une règle empirique utile pour analyser certains types de données. Si la variation entre les mesures est causée par des facteurs aléatoires qui produisent une distribution normale, et que quelqu’un vous indique la moyenne et l’écart-type, vous savez qu’un peu plus des deux tiers des mesures se situent à moins d’un écart-type de part et d’autre de la moyenne. En raison de la forme de la courbe, 95,4 % des mesures sont à l’intérieur de deux écarts-types et 99,7 % des mesures sont à l’intérieur de trois écarts-types. Par exemple, si quelqu’un dit que la taille moyenne des hommes adultes aux États-Unis est de 178 cm (5 pi 10 po) et que l’écart-type est d’environ 8 cm (3 po), vous saurez que 68 % des hommes aux États-Unis ont une taille comprise entre 170 cm (5 pi 7 po) et 186 cm (6 pi 1 po). Vous savez également qu’environ 95 % des hommes adultes aux États-Unis mesurent entre 162 cm (5 pi 4 po) et 194 cm (6 pi 4 po), et que la quasi-totalité d’entre eux (99,7 %) mesurent entre 154 cm (5 pi 1 po) et 202 cm (6 pi et 7 po). Ces chiffres sont connus sous le nom de règle 68-95-99.7.
Exemple : L’essence dans les trois écarts-types
La responsable du contrôle de la qualité de la raffinerie marque les fourchettes comprises entre deux et trois écarts-types, comme le montre la figure 14.3. Certains produits doivent avoir moins de variabilité que d’autres pour atteindre leur objectif. Par exemple, si la qualité d’une formation portant sur l’utilisation de machines hautement spécialisées et potentiellement dangereuses était évaluée, la plupart des personnes participantes devraient dépasser le taux de réussite acceptable. Trois écarts-types par rapport aux limites de contrôle peuvent convenir à certains produits, mais pas à d’autres. En général, si la moyenne se situe à six écarts-types des deux limites de contrôle, la probabilité qu’une pièce dépasse les limites de contrôle en raison d’une variation aléatoire est pratiquement nulle (2 sur 1 milliard).
Exemple : Une étape du projet qui améliore la qualité de l’essence
Un nouveau processus de raffinage est mis en place pour produire des carburants moins variables. La responsable du contrôle de la qualité de la raffinerie prend une nouvelle série d’échantillons et construit un nouveau diagramme de distribution des fréquences, comme le montre la figure 14.4. Elle calcule un nouvel écart-type de 0,2 d’indice d’octane. À partir de là, elle peut utiliser la règle 68-95-99.7 pour estimer que 68,3 % du carburant produit aura un indice d’octane compris entre 86,8 et 87,2 et que 99,7 % du carburant aura un indice d’octane compris entre 86,4 et 87,6. Pour décrire ce degré de contrôle, on peut dire qu’il s’agit d’un système de production à cinq sigma, ce qui fait référence aux cinq écarts-types entre la moyenne et la limite de contrôle de part et d’autre.
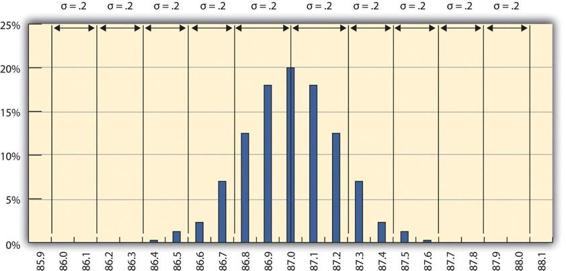
Source : http://pm4id.org/10/1/
Outils d’élaboration d’un plan qualité
On obtient une qualité élevée en la planifiant plutôt qu’en réagissant aux problèmes une fois qu’ils ont été identifiés. Des normes sont choisies et des processus sont mis en place pour atteindre ces normes.
Terminologie de la mesure
Pendant la phase d’exécution du projet, les services et les produits sont échantillonnés et mesurés afin de déterminer si la qualité se situe dans les limites de contrôle des exigences et d’analyser les causes des variations. Cette évaluation est souvent effectuée par un groupe distinct du contrôle de la qualité, et la connaissance de quelques termes relatifs à la mesure des processus est nécessaire pour comprendre leurs rapports. Plusieurs de ces termes sont similaires et il est utile de les distinguer.
Le plan qualité précise les limites de contrôle du produit ou du processus; la taille de l’intervalle entre ces limites est la tolérance. Les tolérances sont souvent écrites comme la valeur moyenne plus ou moins la tolérance. Les signes plus et moins s’écrivent ensemble « ± ».
Exemple : Tolérance dans la production d’essence
La raffinerie de pétrole a choisi de fixer ses limites de contrôle pour l’essence de 87 d’indice d’octane, à 86 et 88. La tolérance est de 87 ± 1.
Des outils sont sélectionnés pour mesurer les échantillons de manière suffisamment précise pour déterminer si les mesures se situent dans les limites de contrôle et si elles révèlent une tendance. Chaque outil de mesure a ses propres tolérances.
Le choix de la tolérance a une incidence directe sur le coût d’obtention de la qualité (COQ). En général, il est plus coûteux de produire et de mesurer des produits présentant de faibles tolérances. Les coûts associés à la fabrication de produits présentant de faibles tolérances de variation peuvent être très élevés et ne pas être proportionnels aux gains. Par exemple, si le coût évalué pour chaque écran créé dans un didacticiel en ligne est supérieur à celui de la livraison du produit et de la résolution des problèmes a posteriori, le COQ risque d’être trop élevé et le concepteur pédagogique tolérera davantage de défauts dans la conception.
Définir les attentes des clients et y répondre
Les clients fournissent des spécifications qui doivent être respectées pour que le projet soit couronné de succès. Rappelons que le respect des spécifications du projet est l’une des définitions de la réussite d’un projet. Les clients ont souvent des attentes qu’il est plus difficile d’exprimer dans le cahier des charges. Par exemple, un client souhaitera être invité à toutes les réunions du projet et sélectionnera ensuite les spécifications qui lui semblent les plus pertinentes. Un autre client souhaitera n’être invité qu’aux réunions de projet qui requièrent sa participation. Inviter ce client à toutes les réunions entraînera des frustrations inutiles. Il est important d’écouter le client pour comprendre ses attentes qui ne sont pas facilement saisissables dans les spécifications et d’y répondre adéquatement.
Les sondages sur les projets permettent de savoir comment le client perçoit le rendement du projet, et fournissent à l’équipe de projet des données utiles pour répondre aux attentes du client. Si les résultats des sondages indiquent que le client n’est pas satisfait de certains aspects du projet, l’équipe de projet a l’occasion d’explorer les raisons de cette perception avec le client et d’élaborer des plans de redressement. Le sondage peut également aider à définir ce qui va bien et ce qui doit être amélioré.
Sources d’information sur la planification
L’élaboration d’un plan qualité fait partie du processus de planification initial. Les premières estimations de la portée, du budget et du calendrier servent à identifier les processus, les services ou les produits pour lesquels le niveau et la qualité attendus doivent être précisés. L’analyse des risques permet de déterminer quels sont les risques susceptibles d’affecter la qualité du projet.
Techniques
Plusieurs outils et techniques sont disponibles pour planifier et contrôler la qualité d’un projet. Le degré d’utilisation de ces outils dépend de la complexité du projet et du programme de gestion de la qualité utilisé par le client.
Les outils d’élaboration d’un plan qualité dont dispose le gestionnaire de projet sont présentés ci-dessous.
L’analyse coûts-avantages consiste à comparer les coûts de vos activités liées à la qualité avec les avantages que vous en retirerez. Les coûts sont faciles à mesurer; les efforts et les ressources nécessaires pour les réaliser sont les mêmes que pour n’importe quelle autre tâche de votre calendrier. Étant donné que les activités liées à la qualité ne donnent pas lieu à la fabrication d’un produit, il est parfois plus difficile d’en mesurer les avantages. Les principaux avantages sont la réduction du nombre de modifications, l’augmentation de la productivité et de l’efficacité, et une plus grande satisfaction de l’équipe et du client.
L’étalonnage consiste à utiliser les résultats du plan qualité d’autres projets pour fixer des objectifs pour le vôtre. Vous pourrez constater que le dernier projet de votre entreprise présentait 20 % moins de défauts que le précédent. Vous devriez vouloir tirer des leçons d’un tel projet et mettre en pratique toutes les idées utilisées pour réaliser une telle amélioration. Les repères peuvent vous donner des points de référence pour juger votre propre projet avant même que vous ne commenciez le travail.
Le plan d’expériences est la liste de tous les types de tests que vous allez effectuer sur votre produit. Il peut énumérer tous les types de procédures de test que vous effectuerez, les approches que vous adopterez et même les tests eux-mêmes. (Dans le monde du logiciel, c’est ce qu’on nomme la planification des tests.)
Le coût d’obtention de la qualité est ce que vous obtenez lorsque vous additionnez le coût de toutes les activités de prévention et d’inspection que vous allez réaliser dans le cadre de votre projet. Il ne s’agit pas seulement des tests. Il comprend le temps passé à rédiger des normes, à réviser des documents, à se réunir pour analyser les causes à l’origine des défectuosités et à retravailler pour les corriger, une fois qu’elles ont été trouvées par l’équipe : en d’autres termes, absolument tout ce que vous faites pour assurer la qualité du projet. Le coût de la qualité peut être un bon chiffre à vérifier pour déterminer si votre projet se porte bien ou s’il connaît des difficultés. Supposons que votre entreprise suive le coût de la qualité pour tous ses projets, vous pourriez alors savoir si vous dépensez plus ou moins par rapport à d’autres projets pour que votre projet réponde aux normes de qualité.
Les graphiques de contrôle peuvent servir à définir les limites acceptables. Si certaines des fonctions d’un projet sont répétitives, les contrôles statistiques du processus peuvent être utilisés pour déterminer les tendances et maintenir les processus dans les limites de contrôle. Une partie de la planification du contrôle de la qualité des processus répétitifs consiste à déterminer les limites de contrôle et la manière dont le processus sera échantillonné.
Les diagrammes de cause à effet peuvent aider à découvrir les problèmes. Lorsque les graphiques de contrôle indiquent une cause attribuable à une variation, il n’est pas toujours facile d’identifier la cause d’un problème. Les discussions visant à découvrir la cause peuvent être facilitées par l’utilisation d’un diagramme de cause à effet ou d’un diagramme en arêtes de poisson, dans lequel les participants sont encouragés à déterminer les causes possibles d’une défectuosité.
Exemple : Représentation graphique des problèmes relatifs à la qualité
Une petite entreprise manufacturière tente de déterminer les causes attribuables aux variations de sa chaîne de fabrication. Une équipe est formée pour définir six possibilités, comme le montre le diagramme en arêtes de poisson de la figure 14.5 : matières premières de mauvaise qualité, fluctuation de la puissance, température ambiante, absentéisme des travailleurs, formation insuffisante, équipement vétuste.
Chaque branche du diagramme peut être développée pour décomposer une catégorie en éléments plus spécifiques. Un ingénieur et un électricien travaillent sur l’une des branches pour étudier les causes possibles de fluctuation de la puissance et ajouter des détails à leur partie du diagramme en arêtes de poisson, comme le montre la figure 14.6.
Les feuilles de contrôle, les histogrammes et les diagrammes de Pareto servent à résoudre plusieurs problèmes relatifs à la qualité. Lorsqu’un problème de contrôle de la qualité survient, le gestionnaire de projet doit choisir le problème à traiter en premier. Pour hiérarchiser les problèmes relatifs à la qualité, il suffit de déterminer ceux qui se produisent le plus fréquemment. Ces données peuvent être collectées à l’aide d’une feuille de contrôle, qui est un formulaire de base sur lequel l’utilisateur peut cocher la case appropriée chaque fois qu’un problème survient, ou en automatisant le processus de collecte de données à l’aide de la technologie appropriée. Une fois les données collectées, elles peuvent être analysées en créant un type de diagramme de distribution de fréquences appelé histogramme. Un véritable histogramme est un diagramme à colonnes dans lequel la largeur des colonnes remplit l’espace disponible sur l’axe des x et est proportionnelle aux valeurs des catégories affichées sur cet axe, tandis que la hauteur des colonnes est proportionnelle à la fréquence des occurrences. La plupart des histogrammes utilisent une largeur de colonne pour représenter une catégorie, tandis que l’axe vertical représente la fréquence des occurrences.
Une variante de l’histogramme est un diagramme de distribution des fréquences inventé par l’économiste Vilfredo Pareto, connu sous le nom de diagramme de Pareto, dans lequel les colonnes sont classées par ordre décroissant, la plus fréquente se trouvant à gauche, et une ligne est ajoutée pour indiquer le total cumulé. La combinaison de colonnes et d’une ligne permet à l’utilisateur de voir en un coup d’œil quels sont les problèmes les plus fréquents et quelle fraction du total ils représentent.
Une fois que vous avez établi votre plan qualité, vous connaissez les lignes directrices relatives à la gestion de la qualité pour ce projet. Vos stratégies de contrôle de la qualité du projet doivent être incluses dans le plan, ainsi que les raisons qui soutiennent toutes les mesures que vous prenez. Il est important que tous les membres de l’équipe comprennent la raison d’être des paramètres utilisés pour juger de la réussite ou de l’échec du projet.
Assurance de la qualité
L’objectif de l’assurance de la qualité est d’amener les gens à avoir confiance dans le bon fonctionnement du plan qualité et des contrôles de qualité. Du temps doit être consacré à l’examen du plan qualité initial et à la comparaison de ce plan avec la manière dont la qualité est assurée au cours de la mise en œuvre du projet.
Analyse du processus
Les organigrammes portant sur les processus de qualité sont comparés aux processus suivis pendant les opérations réelles. Si le plan n’a pas été suivi, le processus est analysé et des mesures correctives sont prises. La mesure corrective peut consister à former les personnes concernées afin qu’elles respectent le plan qualité ou à réviser le plan.
Les expériences qui échantillonnent des produits et des processus et collectent des données sont examinées pour vérifier qu’elles font appel à des techniques d’échantillonnage statistiquement valables et que les méthodes de mesure ont des tolérances suffisamment faibles pour détecter les variations dans les limites de contrôle.
Les projets étant temporaires, les possibilités d’apprentissage et d’amélioration sont moins nombreuses dans le cadre d’un projet, surtout s’il est de courte durée. Cependant, même dans le cas de projets de courte durée, le responsable de la qualité doit pouvoir tirer les leçons de l’expérience et modifier le processus pour le prochain projet d’une complexité similaire.
Exemple : Analyser les processus relatifs à la qualité dans une formation sur la sécurité
Un collège technique chargé de former des employés aux pratiques de sécurité dans l’usine évalue son processus d’embauche des enseignants à la fin de la formation pour voir s’il disposait des meilleurs critères de sélection. Par exemple, le processus exigeait que les enseignants soient titulaires d’une maîtrise en fabrication pour pouvoir enseigner dans un collège. Le collège a réalisé un sondage auprès des anciens étudiants pour leur demander ce qui pourrait améliorer l’enseignement dans les futurs cours sur le sujet. Certains étudiants ont estimé qu’il serait plus important d’exiger que les enseignants aient plus d’années d’expérience en matière de formation, tandis que d’autres ont recommandé qu’ils obtiennent une certification auprès d’un centre de formation. Le collège a examiné ces suggestions et a décidé de maintenir l’exigence d’une maîtrise, mais d’ajouter une exigence selon laquelle les enseignants doivent être certifiés en matière de sécurité des installations.
L’objectif de l’assurance de la qualité est de convaincre le client que les normes et les procédures de qualité sont respectées. Cela se fait par un examen interne du plan, des tests et des politiques de révision ou par un audit des mêmes éléments réalisé par un groupe ou une agence externe.
Attribution
Ce chapitre du livre Gestion de projet est une copie dérivée de Project Management for Instructional Designers par Amado, M., Ashton, K., Ashton, S., Bostwick, J., Clements, G., Drysdale, J., Francis, J., Harrison, B., Nan, V., Nisse, A., Randall, D., Rino, J., Robinson, J., Snyder, A., Wiley, D., & Anonymes. (DATE) Project Management for Instructional Designers. Extrait de http://pm4id.org/ sous Creative Commons Attribution 3.0 non transposé.