5.2: Moving Money Involving Simple Interest

Maturity Value (or Future Value)

The maturity value of a transaction is the amount of money resulting at the end of a transaction, an amount that includes both the interest and the principal together. It is called a maturity value because in the financial world the termination of a financial transaction is known as the “maturing” of the transaction. The amount of principal with interest at some point in the future, but not necessarily the end of the transaction, is known as the future value.

For any financial transaction involving simple interest, the following is true:

[latex]\text{Amount of money at the end}=\text{Amount of money at the beginning} +\text{Interest}[/latex]

Applying algebra, you can summarize this expression by the following equation, where the future value or maturity value is commonly denoted by the symbol [latex]S[/latex].

[latex]S=P+I[/latex]

Substituting in Formula 5.1[latex]I=Prt[/latex] (Simple Interest; see Section 5.1) yields the equation

[latex]S=P+Prt[/latex]

or

[latex]S=P(1+rt)[/latex]

[latex]\boxed{5.2\text{a}}[/latex] Simple Interest Future Value

[latex]\color{red}{S\;}\color{black}{\text{is Maturity Value:}}[/latex] The maturity value is the amount of money resulting at the end of a transaction, including both the interest and the principal.

[latex]\color{blue}{P\;}\color{black}{\text{is Present Value or Principal:}}[/latex] The present value is the amount borrowed or invested at the beginning of a period.

[latex]\color{green}{r\;}\color{black}{\text{is Simple Interest Rate:}}[/latex] The interest rate is the rate of interest that is charged or earned during a specified time period. It is expressed as a percent.

[latex]\color{purple}{t\;}\color{black}{\text{is Time Period:}}[/latex] The time period or term is the length of the financial transaction for which interest is charged or earned.

—

From the future value formula [latex]S=P(1+rt)[/latex] you can derive the present value formula ([latex]P[/latex]):

 [latex]\begin{align*}P=\frac{S}{1+rt}\end{align*}[/latex]

Sometimes you will be required to calculate the simple interest dollar amount ([latex]I[/latex]). the formula is given below. 

[latex]\boxed{5.2\text{b}}[/latex] Simple Interest Amount

[latex]\color{red}{I\;}\color{black}{\text{is Interest Amount:}}[/latex] The interest amount is the dollar amount of interest that is paid or received.

[latex]\color{blue}{S\;}\color{black}{\text{is Maturity Value:}}[/latex] The maturity value is the amount of money resulting at the end of a transaction, including both the interest and the principal.

[latex]\color{green}{P\;}\color{black}{\text{is Present Value or Principal:}}[/latex] The present value is the amount borrowed or invested at the beginning of a period. 

Example 5.2.2

You just inherited [latex]\$35,000[/latex] from your uncle’s estate and plan to purchase a house four months from today. If you use your inheritance as your down payment on the house, how much will you be able to put down if your money earns [latex]4\frac{1}{4}\%[/latex] simple interest? How much interest will you have earned?

Solution

Calculate the amount of money four months from now including both the principal and interest earned. This is the maturity value ([latex]S[/latex]). Also calculate the interest earned ([latex]I[/latex]).

Step 1: Given variables:

[latex]P=\$35,000[/latex];        [latex]t=4\;\text{months}[/latex];        [latex]r=4\frac{1}{4}\%\;\text{per year}[/latex]

Step 2: Express the time in years to match the annual rate.

[latex]\begin{align*}t=\frac{4}{12}\end{align*}[/latex]

Step 3: Solve for the future value, [latex]S[/latex].

[latex]\begin{eqnarray}S&=&P\times(1+rt)\\[1ex]S&=&\$35,000\times\left(1+4\frac14\%\times\frac4{12}\right)\\[1ex]S&=&\$35,\!000\times(1+0.0425\times0.\overline3)\\S&=&\$35,\!495.83\end{eqnarray}[/latex]

Step 4: Solve for the amount of interest, [latex]I[/latex].

[latex]\begin{eqnarray*}I&=&\$35,495.83-\$35,000.00\\I&=&\$495.83\end{eqnarray*}[/latex]

Step 5: Write as a statement.

Four months from now you will have [latex]\$35,495.83[/latex] as a down payment toward your house, which includes [latex]\$35,000[/latex] in principal and [latex]\$495.83[/latex] of interest.

Example 5.2.3

Recall the section opener, where you needed [latex]\$8,000[/latex] for tuition in the fall and the best simple interest rate you could find was [latex]4.5\%[/latex]. Assume you have eight months before you need to pay your tuition. How much money do you need to invest today?

Solution

Calculate the principal amount of money today [latex]P[/latex] that you must invest such that it will earn interest and end up at the [latex]\$8,000[/latex] required for the tuition.

Step 1: Given variables:

[latex]S=\$8,000[/latex];        [latex]r=4.5\%\;\text{per year}[/latex];        [latex]t=8\;\text{months}[/latex]

Step 2: Express the time in years to match the annual rate.

[latex]\begin{align*}t=\frac{8}{12}\end{align*}[/latex]

 

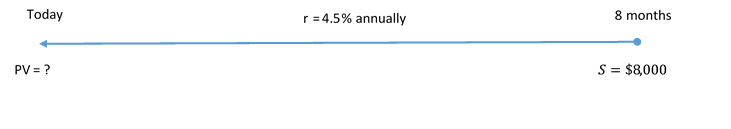
Step 3: Solve for the present value, [latex]P[/latex].

[latex]\begin{eqnarray}P&=&\frac S{1+rt}\\[1ex]P&=&\frac{\$8,000}{(1+4.5\%\times\frac8{12})}\\[1ex]P&=&\frac{\$8,000}{(1+0.045\times0.\overline6)}\\[1ex]P&=&\$7,766.99\end{eqnarray}[/latex]

Step 4: Write as a statement.

If you place [latex]\$7,766.99[/latex] into the investment, it will grow to [latex]\$8,000[/latex] in the eight months.

Equivalent Payments

Late Payments: If a debt is paid late, then a financial penalty that is fair to both parties involved should be imposed. That penalty should reflect a current rate of interest and be added to the original payment. Assume you owe [latex]\$100[/latex] to your friend and that a fair current rate of simple interest is [latex]10\%[/latex]. If you pay this debt one year late, then a [latex]10\%[/latex] late interest penalty of [latex]\$10[/latex] should be added, making your debt payment [latex]\$110[/latex]. This is no different from your friend receiving the [latex]\$100[/latex] today and investing it himself at [latex]10\%[/latex] interest so that it accumulates to [latex]\$110[/latex] in one year.

Early Payments: If a debt is paid early, there should be some financial incentive (otherwise, why bother?). Therefore, an interest benefit, one reflecting a current rate of interest on the early payment, should be deducted from the original payment. Assume you owe your friend [latex]\$110[/latex] one year from now and that a fair current rate of simple interest is [latex]10\%[/latex]. If you pay this debt today, then a [latex]10\%[/latex] early interest benefit of [latex]\$10[/latex] should be deducted, making your debt payment today [latex]\$100[/latex]. If your friend then invests this money at [latex]10\%[/latex] simple interest, one year from now he will have the [latex]\$110[/latex], which is what you were supposed to pay.

Notice in these examples that a simple interest rate of [latex]10\%[/latex] means [latex]\$100[/latex] today is the same thing as having [latex]\$110[/latex] one year from now. This illustrates the concept that two payments are equivalent payments if, once a fair rate of interest is factored in, they have the same value on the same day. Thus, in general you are finding two amounts at different points in time that have the same value, as illustrated in the figure below.

HOW TO

Calculate an Equivalent Payment

The steps required to calculate an equivalent payment are no different from those for single payments. If an early payment is being made, then you know the future value, so you solve for the present value (which removes the interest). If a late payment is being made, then you know the present value, so you solve for the future value (which adds the interest penalty).

Example 5.2.5

Erin owes Charlotte [latex]\$1,500[/latex] today. Unfortunately, Erin had some unexpected expenses and is unable to make her debt payment. After discussing the issue, they agree that Erin can make the payment nine months late and that a fair simple interest rate on the late payment is [latex]5\%[/latex]. Use [latex]9[/latex] months from now as your focal date and calculate how much Erin needs to pay. What is the amount of her late penalty?

Solution

A late payment is a future value amount ([latex]S[/latex]). The late penalty is equal to the interest ([latex]I[/latex]).

Step 1: Given variables:

[latex]P=\$1,500[/latex];        [latex]r=5\%\;\text{annually}[/latex];        [latex]t=9\;\text{months}[/latex]

Step 2: Express the time in years to match the annual rate.

[latex]\begin{align*}t=\frac{9}{12}\end{align*}[/latex]

 

Step 3: Calculate the future value, [latex]S[/latex].

[latex]\begin{eqnarray}S&=&P\times(1+rt)\\[1ex]S&=&\$1,500\times\left(1+5\%\times\frac9{12}\right)\\[1ex]S&=&\$1,500\times(1+0.05\times0.75)\\S&=&\$1,556.25\end{eqnarray}[/latex]

Step 4: Solve for the amount of interest, [latex]I[/latex].

[latex]\begin{eqnarray*}I&=&\$1,556.25-\$1,500.00\\I&=&\$56.25\end{eqnarray*}[/latex]

Step 5: Write as a statement.

Erin’s late payment is for [latex]\$1,556.25[/latex], which includes a [latex]$56.25[/latex] interest penalty for making the payment nine months late.

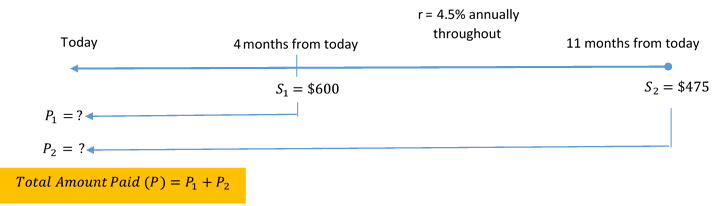
Example 5.2.6

Rupert owes Aminata two debt payments: [latex]\$600[/latex] four months from now and [latex]\$475[/latex] eleven months from now. Rupert came into some money today and would like to pay off both of the debts immediately. Aminata has agreed that a fair interest rate is [latex]7\%[/latex]. Using today as a focal date, what amount should Rupert pay? What is the total amount of his early payment benefit?

An early payment is a present value amount ([latex]P[/latex]). Both payments will be moved to today and summed. The early payment benefit will be the total amount of interest removed ([latex]I[/latex]).

Solution

Step 1: Given variables:

[latex]r=7\%\;\text{annually}[/latex]

The two payments and payment due dates are known.

Payment #1: [latex]S_1=\$600[/latex]; [latex]t=4\;\text{months from now}[/latex]
Payment #2: [latex]S_2=\$475[/latex]; [latex]t=11\;\text{months from now}[/latex]

Replacement payment is being made today (the focal date).

---

Payment #1:

Step 1: Express the time in years to match the annual rate.

 [latex]\begin{align*}t=\frac{4}{12}\end{align*}[/latex]

 

Step 2: Solve for [latex]P_1[/latex].

[latex]\begin{eqnarray*}P_1&=&\frac{S_1}{1+rt}\\[1ex]P_1&=&\frac{\$600}{\left(1+0.07\times0.\overline3\right)}\\[1ex]P_1&=&\$586.32\end{eqnarray*}[/latex]

---

Payment #2:

Step 1: While the rate is annual, the time is in months. Convert the time to an annual number.

[latex]\begin{align*}t=\frac{11}{12}\end{align*}[/latex]

Step 2: Solve for [latex]P_2[/latex].

[latex]\begin{eqnarray}P_2&=&\frac{S_2}{1+rt}\\[1ex]P_2&=&\frac{\$475}{(1+0.07\times0.91\overline6)}\\[1ex]P_2&=&\$446.36\end{eqnarray}[/latex]

---

Step 2: Calculate the total amount of interest, [latex]I[/latex].

Payment #1:

[latex]\begin{eqnarray*}I_1&=&S_1–P_1\\I_1&=&\$600–\$586.32\\I_1&=&\$13.68\end{eqnarray*}[/latex]

Payment #2:

[latex]\begin{eqnarray*}I_2&=&S_2–P_2\\I_2&=&\$475–\$446.36\\I_2&=&\$28.64\end{eqnarray*}[/latex]

Total Interest:

[latex]\begin{eqnarray*}I&=&\$13.68+\$28.64\\I&=&\$42.32\end{eqnarray*}[/latex]

Total Payment:

[latex]\begin{eqnarray}P_\text{total paid today}&=&P_1+P_2\\P_\text{total paid today}&=&\$586.32+\$446.36\\P_\text{total paid today}&=&\$1,032.68\end{eqnarray}[/latex]

Step 3: Write as a statement.

To clear both debts today, Rupert pays [latex]\$1,032.68[/latex], which reflects a [latex]\$42.32[/latex] interest benefit reduction for the early payment.

---

Section 5.2 Exercises

---

In each of the exercises that follow, try them on your own. Full solutions are available should you get stuck.

1. An accountant needs to allocate the principal and simple interest on a loan payment into the appropriate ledgers. If the amount received was [latex]\$10,267.21[/latex] for a loan that spanned April 14 to July 31 at [latex]9.1\%[/latex], how much was the principal and how much was the interest?

Solution

Step 1: Given information:

[latex]S=\$10,267.21[/latex];        [latex]r=9.1\%\;\text{annually}[/latex];        [latex]t=\text{April}\;14\;\text{to July}\;31=108\;\text{days}[/latex]

Step 2: Convert daily [latex]t[/latex] to match annual [latex]r[/latex]:

[latex]\begin{align*}t=\frac{108}{365}\end{align*}[/latex]

Step 3: Solve for [latex]P[/latex].

[latex]\begin{eqnarray*}P&=&\frac S{1+rt}\\[1ex]P&=&\frac{\$10,267.21}{1+0.091\times\frac{108}{365}}\\[1ex]P&=&\$9,998\end{eqnarray*}[/latex]

Step 4: Solve for [latex]I[/latex].

[latex]\begin{eqnarray*}I&=&S-P\\I&=&\$10,267.21-\$9,998\\I&=&\$269.21\end{eqnarray*}[/latex]

Step 5: Write as a statement.

The principal was [latex]\$9,998[/latex] and the simple interest on the loan was [latex]\$269.21[/latex].

 

2. Suppose Robin borrowed [latex]\$3,600[/latex] on October 21 and repaid the loan on February 21 of the following year. What simple interest rate was charged if Robin repaid [latex]\$3,694.63[/latex]?

Solution

Step 1: Given information:

[latex]P=\$3,600[/latex];        [latex]S=\$3,694.63[/latex];        [latex]t=\text{October}\;21\;\text{to February}\;21=123\;\text{days}[/latex]

Step 2: Compute [latex]I[/latex].

[latex]\begin{eqnarray*}I&=&S-P\\I&=&\$3,694.63-\$3,600\\I&=&\$94.63\end{eqnarray*}[/latex]

Step 3: Convert daily [latex]t[/latex] to match annual [latex]r[/latex]:

[latex]\begin{align*}t=\frac{123}{365}\end{align*}[/latex]

Step 4: Solve for [latex]r[/latex]:

[latex]\begin{eqnarray*}r&=&\frac I{Pt}\\[1ex]r&=&\frac{\$94.63}{\$3,600\left(\frac{123}{365}\right)}\\[1ex]r&=&0.078004\;\text{or}\;7.8004\%\end{eqnarray*}[/latex]

Step 5: Write as a statement.

The simple interest charged was [latex]7.80\%[/latex].

3.  Jayne needs to make three payments to Jade requiring [latex]\$2,000[/latex] each [latex]5[/latex] months, [latex]10[/latex] months, and [latex]15[/latex] months from to day. She proposes instead making a single payment eight months from today. If Jade agrees to a simple interest rate of [latex]9.5\%[/latex], what amount should Jayne pay?

Solution

Step 1: Given information:

[latex]r=9.5\%\;\text{annually}[/latex]

Payment #1: [latex]P=\$2,000[/latex]; [latex]t=8\;\text{months}−5\;\text{months}=3\;\text{months}[/latex]

Payment #2: [latex]S=\$2,000[/latex]; [latex]t=10\;\text{months}−8\;\text{months}=2\;\text{months}[/latex]

Payment #3: [latex]S=$2,000[/latex]; [latex]t=15\;\text{months}−8\;\text{months}=7\;\text{months}[/latex]

---

Payment #1:

Step 1: Convert monthly [latex]t[/latex] to match annual [latex]r[/latex]:

[latex]\begin{align*}t=\frac{3}{12}\end{align*}[/latex]

Step 2: Solve for [latex]S[/latex]:

[latex]\begin{eqnarray*}S&=&P\left(1+rt\right)\\[1ex]S&=&\$2,000\times\left(1+0.095\times\frac3{12}\right)\\[1ex]S&=&\$2,000\times1.02375\\S&=&\$2,047.50\end{eqnarray*}[/latex]

---

Payment #2:

Step 2: Convert monthly [latex]t[/latex] to match annual [latex]r[/latex]:

[latex]\begin{align*}t=\frac{2}{12}\end{align*}[/latex]

Step 3: Solve for [latex]P[/latex]:

[latex]\begin{eqnarray*}P&=&\frac S{1+rt}\\[1ex]P&=&\frac{\$2,000}{1+0.095\times\frac2{12}}\\[1ex]P&=&\frac{\$2,000}{1.0158\overline3}\\[1ex]P&=&\$1,968.83\end{eqnarray*}[/latex]

---

Payment #3:

Step 2: Convert monthly [latex]t[/latex] to match annual [latex]r[/latex]:

[latex]\begin{align*}t=\frac{7}{12}\end{align*}[/latex]

Step 3: Solve for [latex]P[/latex]:

[latex]\begin{eqnarray*}P&=&\frac S{1+rt}\\[1ex]P&=&\frac{\$2,000}{1+0.095\times\frac7{12}}\\[1ex]P&=&\frac{\$2,000}{1.05541\overline6}\\P&=&\$1,894.99\end{eqnarray*}[/latex]

[latex]\begin{eqnarray*}\text{Replacement payment eight months from today}&=&\$2,047.50+\$1,968.83+\$1,894.99\\\text{Replacement payment eight months from today}&=&\$5,911.32\end{eqnarray*}[/latex]

---

Step 2: Write as a statement.

Jayne should pay [latex]\$5,911.32[/latex].

THE FOLLOWING LATEX CODE IS FOR FORMULA TOOLTIP ACCESSIBILITY. NEITHER THE CODE NOR THIS MESSAGE WILL DISPLAY IN BROWSER.[latex]I=Prt[/latex]

---

Attribution

“8.2: Moving Money Involving Simple Interest” from Business Math: A Step-by-Step Handbook Abridged by Sanja Krajisnik; Carol Leppinen; and Jelena Loncar-Vines is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.