2.6: Linear Equations: Manipulating and Solving
Introduction
You are shopping at Old Navy for seven new outfits. The price points are [latex]\$10[/latex] and [latex]\$30[/latex]. You really like the [latex]\$30[/latex] outfits; however, your total budget can’t exceed [latex]\$110[/latex]. How do you spend [latex]\$110[/latex] to acquire all the needed outfits without exceeding your budget while getting as many [latex]\$30[/latex] items as possible?
This is a problem of linear equations, and it illustrates how you can use them to make an optimal decision. Let [latex]L[/latex] represent the quantity of clothing at the low price point of [latex]\$10[/latex], and [latex]H[/latex] represent the quantity of clothing at the high price point of [latex]\$30[/latex]. This results in the following algebraic equations:
[latex]\begin{eqnarray*}L\;+\;H\;&=&\;7\;\text{(the total number of outfits you need)}\\\$10L+\$30H\;&=&\;\$110\;\text{(your total budget)}\end{eqnarray*}[/latex]
By simultaneously solving these equations you can determine how many outfits at each price point you can purchase.
You will encounter many situations like this in your business career, for example, in making the best use of a manufacturer’s production capacity. Assume your company makes two products on the same production line and sells all its output. Each product contributes differently to your profitability, and each product takes a different amount of time to manufacture. What combination of each of these products should you make such that you operate your production line at capacity while also maximizing the profits earned? This section explores how to solve linear equations for unknown variables.
Understanding Equations
To manipulate algebraic equations and solve for unknown variables, you must first become familiar with some important language, including linear versus nonlinear equations and sides of the equation.
[latex]{\color{blue}{4}}{\color{green}{x}}{\color{blue}{+}}{\color{blue}{3}}{\text{ is the Left side:}}[/latex] Every equation has two sides. Everything to the left side of the equal sign is known as the left side of the equation.
[latex]{\color{red}{-}}{\color{red}{2}}{\color{green}{x}}{\color{red}{-}}{\color{red}{3}}{\text{ is the Right side:}}[/latex] Everything to the right side of the equal sign is known as the right side of the equation.
[latex]{\color{green}{x}}{\;}{\text{is the Variable x:}}[/latex] Observe two important features of this variable:
-
- Note that the variable has an exponent of [latex]1[/latex]. So if you were to plot each algebraic expression onto a Cartesian coordinate system, the expressions would form straight lines (see Figure 2.6.1a). Such equations are called linear equations. Because each equation has only one variable, there is only one solution that makes the equation true. In business mathematics, this is the most common situation you will encounter.
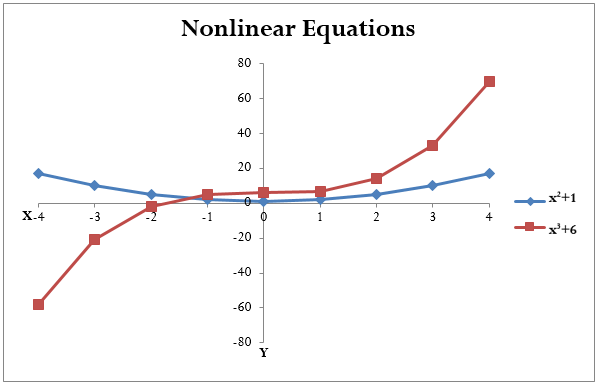
- If the exponent is anything but a one, the equation is a nonlinear equation since the graph of the expression does not form a straight line. Figure 2.5.1b illustrates two algebraic expressions where the exponent is other than a [latex]1[/latex].
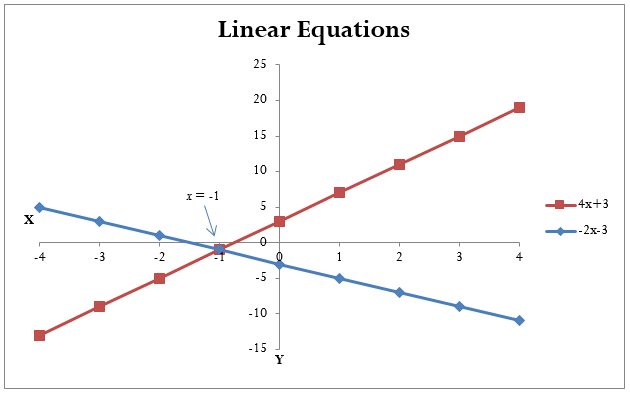
The goal in manipulating and solving a linear equation is to find a value for the unknown variable that makes the equation true. If you substitute a value of [latex]x =−1[/latex] into the above example, the left-hand side of the equation equals the right-hand side of the equation (see Figure 2.6a). The value of [latex]x =−1[/latex] is known as the root, or solution, to the linear equation.
Solving One Linear Equation with One Unknown Variable
In your study of solving linear equations, you need to start by manipulating a single equation to solve for a single unknown variable. Later in this section you will extend from this foundation to the solution of two linear equations with two unknowns.
HOW TO
Determine the root of a linear equation with only one unknown variable
Apply the following steps:
Step 1: Your first goal is to separate the terms containing the literal coefficient from the terms that only have numerical coefficients. Collect all of the terms with literal coefficients on only one side of the equation and collect all of the terms with only numerical coefficients on the other side of the equation. It does not matter which terms go on which side of the equation, so long as you separate them.
Step 2: To move a term from one side of an equation to another, take the mathematical opposite of the term being moved and add it to both sides.
For example, if you want to move the [latex]+3[/latex] in [latex]4x+3=−2x−3[/latex] from the left-hand side to the right-hand side, the mathematical opposite of [latex]+3[/latex] is [latex]−3[/latex]. When you move a term, remember the cardinal rule: What you do to one side of an equation you must also do to the other side of the equation. Breaking this rule breaks the equality in the equation.
Step 3: Combine all like terms on each side and simplify the equation according to the rules of algebra.
Step 4: In the term containing the literal coefficient, reduce the numerical coefficient to a [latex]1[/latex] by dividing both sides of the equation by the numerical coefficient.
 Key Takeaway
Key Takeaway
When you are unsure whether your calculated root is accurate, an easy way to verify your answer is to take the original equation and substitute your root in place of the variable. If you have the correct root, the left-hand side of the equation equals the right-hand side of the equation. If you have an incorrect root, the two sides will be unequal. The inequality typically results from one of the three most common errors in algebraic manipulation:
-
- The rules of BEDMAS have been broken.
- The rules of algebra have been violated.
- What was done to one side of the equation was not done to the other side of the equation.
Things To Watch Out For
When you move a term from one side of the equation to another using multiplication or division, remember that this affects each and every term on both sides of the equation. To remove the [latex]x[/latex] from the denominator in the following equation, multiply both sides of the equation by [latex]x[/latex]:
[latex]\begin{align*}\frac5x+\frac1x=\frac2x+2\end{align*}[/latex]
becomes:
[latex]\begin{align*}x\left(\frac5x+\frac1x\right)=\left(\frac2x+2\right)x\end{align*}[/latex]
which then becomes:
[latex]5+1=2+2x[/latex]
Multiplying every term on both sides by [latex]x[/latex] maintains the equality.
 Paths To Success
Paths To Success
Negative numbers can cause some people a lot of grief. In moving terms from a particular side of the equation, many people prefer to avoid negative numerical coefficients in front of literal coefficients. Revisiting [latex]4x+3=-2x−3[/latex], you could move the [latex]4x[/latex] from the left side to the right side by subtracting [latex]4x[/latex] from both sides. However, on the right side this results in [latex]−6x[/latex]. The negative is easily overlooked or accidentally dropped in future steps. Instead, move the variable to the left side of the equation, yielding a positive coefficient of [latex]6x[/latex].
Example 2.6.1
Take the ongoing example in this section and solve it for [latex]x[/latex]:
[latex]4x+3=−2x−3[/latex].
Solution
Step 1: Move terms with literal coefficients to one side and terms with only numerical coefficients to the other side. Let’s collect the literal coefficient on the left-hand side of the equation. Move [latex]−2x[/latex] to the left-hand side by placing [latex]+2x[/latex] on both sides.
On the right-hand side, the [latex]−2x[/latex] and [latex]+2x[/latex] cancel out to zero.
[latex]4x+3{\color{red}{+}}{\color{red}{2}}{\color{red}{x}}=-2x-3{\color{red}{+}}{\color{red}{2}}{\color{red}{x}}[/latex]
Step 2: All of the terms with the literal coefficient are now on the left. Let’s move all of the terms containing only numerical coefficients to the right-hand side. Move the [latex]+3[/latex] to the right-hand side by placing [latex]−3[/latex] on both sides.
On the left-hand side, the [latex]+3[/latex] and [latex]−3[/latex] cancel out to zero.
[latex]4x+3+2x{\color{blue}{-}}{\color{blue}{3}}=-3{\color{blue}{-}}{\color{blue}{3}}[/latex]
Step 3: The terms are now separated. Combine like terms according to the rules of algebra.
[latex]6x=-6[/latex]
Step 4: The term with the literal coefficient is being multiplied by the numerical coefficient of [latex]6[/latex]. Therefore, divide both sides by [latex]6[/latex].
The left-hand side numerical coefficients will divide to [latex]1[/latex]. Resolve the numerical coefficients on the right-hand side.
[latex]\begin{eqnarray*}{\frac{\cancel6x}{\color{green}{\cancel6}}}{}&=&{\frac{-\cancel6}{\color{green}{\cancel6}}}\\{x}{}&=&{-}{1}\end{eqnarray*}[/latex]
Step 5: Write a statement.
The root of the equation is [latex]x=-1[/latex].
Step 6: Substitute back into the equation to check.
[latex]\begin{eqnarray*}4({\color{red}{-}}{\color{red}{1}})+3&=&-2({\color{red}{-}}{\color{red}{1}})-3\\{\color{red}{-}}{\color{red}{4}}+3&=&{\color{red}{2}}-3\\-1&=&-1\;\checkmark\end{eqnarray*}[/latex]
Example 2.6.2
Solve the following equation for [latex]m[/latex]:
[latex]\begin{align*}\frac{3m}4+2m=4m-15\end{align*}[/latex].
Solution
Step 1: Simplify all fractions to make the equation easier to work with.
Still simplifying, collect like terms where possible.
[latex]{\color{red}{0.75}}m\;+\;2m\;=\;4m\;-\;15[/latex]
Step 2: Collect all terms with the literal coefficient on one side of the equation. Move all terms with literal coefficients to the right-hand side.
[latex]{\color{red}{2.75}}m\;=\;4m\;-\;15[/latex]
Step 3: Combine like terms and move all terms with only numerical coefficients to the left-hand side.
[latex]2.75m\;{\color{red}{-}}\;{\color{red}{2}}{\color{red}{.}}{\color{red}{75}}m\;=\;4m\;-\;15\;{\color{red}{-}}\;{\color{red}{2}}{\color{red}{.}}{\color{red}{75}}m[/latex]
On the left-hand side, the [latex]+2.75m[/latex] and [latex]−2.75m[/latex] cancel each other out. Now move the numerical coefficients to the left-hand side.
[latex]{\color{blue}{0}}\;=\;4m\;-\;15\;{\color{red}{-}}{\;}{\color{red}{2}}{\color{red}{.}}{\color{red}{75}}m[/latex]
On the right-hand side, the [latex]−15[/latex] and [latex]+15[/latex] cancel each other out.
[latex]0\;{\color{blue}{+}}{\;}{\color{blue}{15}}\;=\;4m\;-\;15\;-\;2.75m\;{\color{blue}{+}}{\;}{\color{blue}{15}}[/latex]
Step 4: Combine like terms on each side.
[latex]{0}{\;}{+}{\;}{\color{blue}{15}}{\;}{=}{\;}{4}{m}{\;}{-}{\;}{2}{.}{75}{m}[/latex]
Step 5: Divide both sides by the numerical coefficient that accompanies the literal coefficient.
Simplify.
[latex]\begin{eqnarray*}15\;&=&\;1.25m\\[1ex]\frac{15}{{\color{blue}{1}}{\color{blue}{.}}{\color{blue}{25}}}\;&=&\;\frac{1.25m}{{\color{blue}{1}}{\color{blue}{.}}{\color{blue}{25}}}\\[1ex]12&=&m\end{eqnarray*}[/latex]
Step 6: Write a statement.
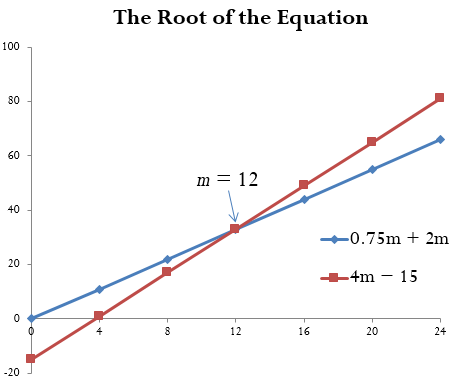
The root of the equation is [latex]m=12[/latex].
This makes both sides of the equation ([latex]\frac{3m}4+2m[/latex] and [latex]4m-15[/latex]) equal [latex]33[/latex].
Example 2.6.3
Solve the following equation for b and round your answer to four decimals: [latex]\frac58b+\frac25=\frac{17}{20}-\frac b4[/latex].
Solution
Step 1: Simplify the fractions and convert to decimals.
[latex]{\color{red}{0}}{\color{red}{.}}{\color{red}{625}}b+{\color{red}{0}}{\color{red}{.}}{\color{red}{4}}={\color{red}{0}}{\color{red}{.}}{\color{red}{85}}-{\color{red}{0}}{\color{red}{.}}{\color{red}{25}}b[/latex]
Step 2: Move the literal coefficient terms to the left-hand side.
The literal coefficients on the right-hand side cancel each other out.
[latex]\begin{eqnarray*}0.625b+0.4+{\color{blue}{0}}{\color{blue}{.}}{\color{blue}{25}}{\color{blue}{b}}&=&0.85{\color{blue}{\cancel{-{0}{.}{25}{b}+0.25b}}}\\{0}{.}{625}{b}{+}{0}{.}{4}{+}{0}{.}{25}{b}{}&=&{0}{.}{85}\end{eqnarray*}[/latex]
Step 3: Move the numerical coefficient terms to the right-hand side.
The numerical coefficients on the left-hand side cancel each other out.
[latex]\begin{eqnarray*}{0}{.}{625}{b}{\cancel{+0.4}}{+}{0}{.}{25}{b}{\color{red}{\cancel{-0.4}}}{}&=&{0}{.}{85}{\color{red}{-}}{\color{red}{0}}{\color{red}{.}}{\color{red}{4}}\\{0}{.}{625}{b}{+}{0}{.}{25}{b}{}&=&{0}{.}{85}{-}{0}{.}{4}\end{eqnarray*}[/latex]
Step 4: Combine like terms on each side.
[latex]0.875b=0.45[/latex]
Step 5: Divide both sides by the numerical coefficient that accompanies the literal coefficient.
[latex]\begin{align*}\frac{0.875b}{{\color{purple}{0}}{\color{purple}{.}}{\color{purple}{875}}}=\frac{0.45}{{\color{purple}{0}}{\color{purple}{.}}{\color{purple}{875}}}\end{align*}[/latex]
Step 6: Simplify.
[latex]b=0.514285[/latex]
Step 7: Round to four decimals as instructed and write a statement.
[latex]b=0.5143[/latex]
Step 8: Write as a statement.
The root is [latex]b=0.5143[/latex].
Solving Two Linear Equations with Two Unknown Variables
The manipulation process you have just practiced works well for solving one linear equation with one variable. But what happens if you need to solve two linear equations with two variables simultaneously? Remember when you were at Old Navy purchasing seven outfits earlier in this chapter? You needed to stay within a pricing budget. Each equation had two unknown variables representing the number of lower-priced outfits ([latex]L[/latex]) and higher-priced outfits ([latex]H[/latex]).
[latex]\begin{eqnarray*}L\;+\;H\;&=&\;7\;\text{(the total number of outfits you need)}\\\$10L+\$30H\;&=&\;\$110\;\text{(your total budget)}\end{eqnarray*}[/latex]
The goal is to reduce two equations with two unknowns into a single linear equation with one unknown. Once this transformation is complete, you then identify the unknown variable by applying the three-step procedure for solving one linear equation, as just discussed.
When you work with two linear equations with two unknowns, the rules of algebra permit the following two manipulations:
- What you do to one side of the equation must be done to the other side of the equation to maintain the equality. Therefore, you can multiply or divide any equation by any number without changing the root of the equation.
- For example, if you multiply all terms of [latex]x + y = 2[/latex] by [latex]2[/latex] on both sides, resulting in [latex]2x + 2y = 4[/latex], the equality of the equation remains unchanged and the same roots exist.
- Terms that are on the same side of an equation can be added and subtracted between equations by combining like terms. Each of the two equations has a left side and right side. This rule permits taking the left side of the first equation and either adding or subtracting like terms on the left side of the second equation. When you perform this action, remember the first rule above. If you add the left sides of the equations together, you then must add the right side of both equations together to maintain equality.
HOW TO
Solve two linear equations with two unknown variables
Step 1: Write the two equations one above the other, vertically lining up terms that have the same literal coefficients and terms that have only the numerical coefficient. If necessary, the equations may need to be manipulated such that all of the literal coefficients are on one side with the numerical coefficients on the other side.
Step 2: Examine your two equations. Through multiplication or division, make the numerical coefficient on one of the terms containing a literal coefficient exactly equal to its counterpart in the other equation.
Step 3: Add or subtract the two equations as needed so as to eliminate the identical term from both equations.
Step 4: In the new equation, solve for the last literal coefficient.
Step 5: Substitute the root of the known literal coefficient into either of the two original equations. If one of the equations takes on a simpler structure, pick that equation.
Step 6: Solve your chosen equation for the other literal coefficient.
 Paths To Success
Paths To Success
Sometimes it is unclear exactly how you need to multiply or divide the equations to make two of the terms identical. For example, assume the following two equations:
[latex]4.9x + 1.5y = 38.3[/latex]
[latex]2.7x − 8.6y = 17.8[/latex]
If the goal is to make the terms containing the literal coefficient [latex]x[/latex] identical, there are two alternative solutions:
- Take the larger numerical coefficient for [latex]x[/latex] and divide it by the smaller numerical coefficient. The resulting number is the factor for multiplying the equation containing the smaller numerical coefficient. In this case, [latex]4.9\;\div\;2.7\;=\;1.\overline{814}[/latex]. Multiply all terms in the second equation by [latex]1.\overline{814}[/latex] to make the numerical coefficients for [latex]x[/latex] equal to each other, resulting in this pair of equations:
[latex]\begin{eqnarray*}4.9x+1.5y&=&38.3\\&\text{and}\;\\4.9x-15.6\overline{074}y&=&32.3\overline{037}\;\text{(every term multiplied by 1.}\overline{\text{814}}\text{)}\end{eqnarray*}[/latex]
- Take the first equation and multiply it by the numerical coefficient in the second equation. Then take the second equation and multiply it by the numerical coefficient in the first equation. In this case, multiply all terms in the first equation by [latex]2.7[/latex]. Then multiply all terms in the second equation by [latex]4.9[/latex].
[latex]13.23x+4.05y=103.41(\text{every term multiplied by 2.7})[/latex]
[latex]13.23x-42.14y=87.22(\text{every term multiplied by 4.9})[/latex]
Note that both approaches successfully result in both equations having the same numerical coefficient in front of the literal coefficient [latex]x[/latex].
 Paths To Success
Paths To Success
Ultimately, every pairing of linear equations with two unknowns can be converted into a single equation through substitution. To make the conversion, do the following:
-
- Solve either equation for one of the unknown variables.
- Take the resulting algebraic expression and substitute it into the other equation. This new equation is solvable for one of the unknown variables.
- Substitute your newfound variable into one of the original equations to determine the value for the other unknown variable.
Take the following two equations:
[latex]a+b=4[/latex] and [latex]2a+b=6[/latex]
-
- Solving the first equation for [latex]a[/latex] results in [latex]a = 4-b[/latex].
- Substituting the expression for [latex]a[/latex] into the second equation and solving for [latex]b[/latex] results in [latex]2(4-b) b=6[/latex], which solves as [latex]b=2[/latex].
- Finally, substituting the root of [latex]b[/latex] into the first equation to calculate [latex]a[/latex] gives [latex]a + 2 = 4[/latex] resulting in [latex]a = 2[/latex]. Therefore, the roots of these two equations are [latex]a = 2[/latex] and [latex]b = 2[/latex].
Example 2.6.4
Recall from the section opener that in shopping for outfits there are two price points of [latex]\$10[/latex] and [latex]\$30[/latex], your budget is [latex]\$110[/latex], and that you need seven articles of clothing. The equations below represent these conditions. Identify how many low-priced outfits ([latex]L[/latex]) and high-priced outfits ([latex]H[/latex]) you can purchase.
[latex]\begin{eqnarray*}L + H &=& 7\\\$10L+\$30H &=& \$110\end{eqnarray*}[/latex]
Solution
Step 1: Write the equations one above the other and line them up.
[latex]\begin{eqnarray*}L + H &=& 7\\\$10L+\$30H &=& \$110\end{eqnarray*}[/latex]
Step 2: Multiply all terms in the first equation by [latex]10[/latex] so that [latex]L[/latex] has the same numerical coefficient in both equations.
[latex]\begin{eqnarray*}{\color{red}{10}}L+{\color{red}{10}}H&=&{\color{red}{70}}\\\$10L+\$30H&=&\$110\end{eqnarray*}[/latex]
Step 3: Subtract the equations by subtracting all terms on both sides.
[latex]\begin{eqnarray*}10L+10H&=&70\\\$10L+30\$H&=&\$110\\{\color{blue}{-}}{\color{blue}{\$}}{\color{blue}{20}}{\color{blue}{H}}{}&=&{\color{blue}{-}}{\color{blue}{\$}}{\color{blue}{40}}\end{eqnarray*}[/latex]
Step 4: Solve for [latex]H[/latex] by dividing both sides by [latex]−20[/latex].
[latex]\begin{eqnarray*}{\frac{-\$20H}{{\color{red}{-}}{\color{red}{\$}}{\color{red}{20}}}}{}&=&{\frac{-\$40}{{\color{red}{-}}{\color{red}{\$}}{\color{red}{20}}}}\\{\color{red}{H}}{}&=&{\color{red}{2}}\end{eqnarray*}[/latex]
Step 5: Substitute the known value for [latex]H[/latex] into one of the original equations. The first equation is simple, so choose that one.
[latex]\begin{eqnarray*}{L}{\;}{+}{\;}{H}{\;}{}&=&{\;}{7}{\;}{\;}\\{L}{\;}{+}{\;}{\color{red}{2}}{\;}{}&=&{\;}{7}\end{eqnarray*}[/latex]
Step 6: Solve for [latex]L[/latex] by subtracting [latex]2[/latex] from both sides. You now have the roots for [latex]L[/latex] and [latex]H[/latex].
[latex]\begin{eqnarray*}L\;+\;2\;{\color{blue}{-}}{\;}{\color{blue}{2}}\;&=&\;7\;{\color{blue}{-}}{\;}{\color{blue}{2}}\;\;\\{\color{blue}{L}}{\;}{}&=&{\;}{\color{blue}{5}}\end{eqnarray*}[/latex]
 Paths To Success
Paths To Success
One of the most difficult areas of mathematics involves translating words into mathematical symbols and operations. To assist in this translation, the table below lists some common language and the mathematical symbol that is typically associated with the word or phrase.
| Language | Math Symbol | ||
|---|---|---|---|
|
|
|
+ |
|
|
|
− |
|
|
|
× |
|
|
|
÷ |
|
|
|
= |
|
> | ||
|
< | ||
|
≥ | ||
|
≤ | ||
|
≠ | ||
Example 2.6.5
Tinkertown Family Fun Park charges [latex]\$15[/latex] for a child wrist band and [latex]\$10.50[/latex] for an adult wrist band. On a warm summer day, the amusement park had total wrist band revenue of [latex]\$15,783[/latex] from sales of [latex]1,279[/latex] wrist bands. How many adult and child wrist bands did the park sell that day?
Solution
Step 1: Write out what you know.
The price of the wrist bands, total quantity, and sales are known.
[latex]\begin{eqnarray*}\text{Child wrist band price}&=&\$15\;\;\\\text{Adult wrist band price}&=&\$10.50\;\;\\\text{Total revenue}&=&\$15,783\;\;\\\text{Total unit sales}&=&1,279\;\;\;\;\end{eqnarray*}[/latex]
The quantity of adult wrist bands sold and the quantity of child wrist bands sold are unknown:
[latex]\begin{eqnarray*}\text{Adult wrist bands quantity}&=&a\;\\\text{Child wrist bands quantity}&=&c\end{eqnarray*}[/latex]
Step 2: Write out how you will get to the solution.
Work with the quantities first. Calculate the total unit sales by adding the number of adult wrist bands to the number of child wrist bands:
[latex]\begin{eqnarray*}{\color{red}{\text{# of adult wrist bands}}}\text{ + }{\color{blue}{\text{# of child wrist bands}}}\text{ }&=&\text{total unit sales}\\{\color{red}{a}}\;+\;{\color{blue}{c}}\;&=&\;1,279\end{eqnarray*}[/latex]
Now consider the dollar figures. Total revenue for any company is calculated as unit price multiplied by units sold. In this case, you must sum the revenue from two products to get the total revenue.
[latex]\begin{eqnarray*}{\color{red}{\text{Total adult revenue}}}\text{ + }{\color{blue}{\text{Total child revenue}}}\;&=&\;\text{Total revenue}\\\text{(}{\color{red}{\text{Adult price×Adult quantity}}}\text{)+(}{\color{blue}{\text{Child price×Child quantity}}}\text{)}&=&\text{Total revenue}\\{\color{red}{\$}}{\color{red}{10}}{\color{red}{.}}{\color{red}{50}}{\color{red}{a}}\;+\;{\color{blue}{\$}}{\color{blue}{15}}{\color{blue}{c}}\;&=&\;\$15,783\end{eqnarray*}[/latex]
Step 3: Write the equations one above the other and line them up.
[latex]\begin{eqnarray*}a+\;c&=&1,279\;\;\\\$10.50a+\$15c&=&\$15,783\end{eqnarray*}[/latex]
Step 4: Multiply all terms in the first equation by [latex]10.5[/latex], resulting in a having the same numerical coefficient in both equations.
[latex]\begin{eqnarray*}{\color{red}{10}}{\color{red}{.}}{\color{red}{50}}a+{\color{red}{10}}{\color{red}{.}}{\color{red}{50}}c&=&13,429.50\;\;\\\${\color{red}{10}}{\color{red}{.}}{\color{red}{50}}a+\$15c&=&\$15,783\end{eqnarray*}[/latex]
Step 5: Subtract the equations by subtracting all terms on both sides.
[latex]\begin{eqnarray*}10.5a+10.5c&=&13,429.50\\\$10.50a+\$15c&=&\$15,783\;\;\text{Subract.}\\{\color{blue}{-}}{\color{blue}{4}}{\color{blue}{.}}{\color{blue}{5}}{\color{blue}{c}}{}&=&{\color{blue}{-}}{\color{blue}{2}}{\color{blue}{,}}{\color{blue}{353}}{\color{blue}{.}}{\color{blue}{50}}\end{eqnarray*}[/latex]
Step 6: Solve for [latex]c[/latex] by dividing both sides by [latex]−4.5[/latex].
[latex]\begin{eqnarray*}{\frac{-4.5c}{{\color{purple}{-}}{\color{purple}{4}}{\color{purple}{.}}{\color{purple}{5}}}}{}&=&{\frac{-2,353.50}{{\color{purple}{-}}{\color{purple}{4}}{\color{purple}{.}}{\color{purple}{5}}}}\\{\color{purple}{c}}{\;}{}&=&{\;}{\color{purple}{523}}\end{eqnarray*}[/latex]
Step 7: Substitute the known value for [latex]c[/latex] into one of the original equations. The first equation is simple, so choose that one.
Solve for a by subtracting [latex]523[/latex] from both sides. You now have the roots for [latex]a[/latex] and [latex]c[/latex].
[latex]\begin{eqnarray*}a+c&=&1,279\\a+{\color{purple}{523}}&=&1,279\\a+{\color{purple}{\cancel{523-523}}}&=&1,279-{\color{purple}{523}}\\a&=&756\end{eqnarray*}[/latex]
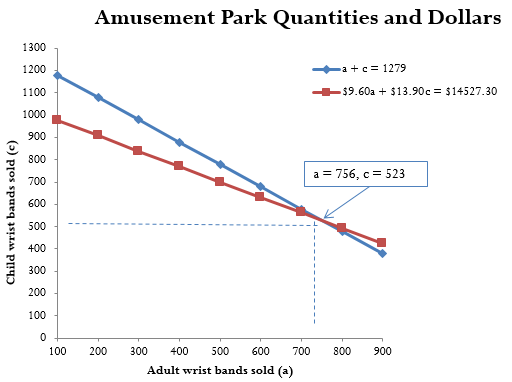
Step 8: Write as a statement.
Tinkertown Family Fun Park sold [latex]523[/latex] child wrist bands and [latex]756[/latex] adult wrist bands.
Section 2.6 Exercises
Mechanics
Solve the following equations for the unknown variable.
- [latex]3(x−5)=15[/latex]
- [latex]12b−3=4+5b[/latex]
- [latex]0.75(4m+12)+15−3(2m+6)=5(−3m+1)+25[/latex]
Solve each of the following pairs of equations for both unknown variables.
- [latex]\begin{align*}x+y&=6\\3x−2y&=8\end{align*}[/latex]
- [latex]\begin{align*}4h−7q&=13\\6h+3q&=33\end{align*}[/latex]
- [latex]\begin{align*}0.25a+\frac{5b}{2}&=3.5\\[1ex]\frac{3a}{4}-\frac{b}{0.2}&=3\end{align*}[/latex]
Solutions
- [latex]x=1.0[/latex]
- [latex]b=1[/latex]
- [latex]m=2[/latex]
- [latex]x=4[/latex], [latex]y=2[/latex]
- [latex]h=5[/latex], [latex]q=1[/latex]
- [latex]a=8[/latex], [latex]b=0.6[/latex]
Applications
In questions 7 and 8, solve the equation for the unknown variable.
- [latex]\begin{align*}\frac{4y}{1.025^4}+y-2y\left(1.05\right)^2=\$1,500\end{align*}[/latex]
- [latex]\$2,500(1+0.06t)+\$1,000(1+0.04t)=\$3,553.62[/latex]
For exercises 9–14, read each question carefully and solve for the unknown variable(s).
- Pamela is cooking a roast for a 5:30 p.m. dinner tonight. She needs to set a delay timer on her oven. The roast takes [latex]1[/latex] hour and [latex]40[/latex] minutes to cook. The time right now is 2:20 p.m. How long of a delay must she set the oven for (before it automatically turns on and starts to cook the roast)?
- In 2010, [latex]266\;\text{million}[/latex] North Americans were using the Internet, which represented a [latex]146.3\%[/latex] increase in Internet users over the year 2000. How many North American Internet users were there in 2000?
- A human resource manager is trying to estimate the cost of a workforce accident. These costs usually consist of direct costs (such as medical bills, equipment damage, and legal expenses) and indirect costs (such as decreased output, production delays, and fines). From past experience, she knows that indirect costs average six times as much as direct costs. If she estimates the cost of an accident to be [latex]\$21,000[/latex], what is the direct cost of the accident?
- In 2011, Canadian federal tax rates were [latex]0\%[/latex] on the first [latex]\$10,527[/latex] of gross income earned, [latex]15\%[/latex] on the next [latex]\$31,017[/latex], [latex]22\%[/latex] on the next [latex]\$41,544[/latex], [latex]26\%[/latex] on the next [latex]\$45,712[/latex], and [latex]29\%[/latex] on anything more. If a taxpayer paid [latex]\$28,925.35[/latex] in federal tax, what was her gross annual income for 2011?
- St. Boniface Hospital raises funds for research through its Mega Lottery program. In this program, [latex]16,000[/latex] tickets are available for purchase at a price of one for [latex]\$100[/latex] or three for [latex]\$250[/latex]. This year, the lottery sold out with sales of [latex]\$1,506,050[/latex]. To better plan next year’s lottery, the marketing manager wants to know how many tickets were purchased under each option this year.
- An accountant is trying to allocate production costs from two different products to their appropriate ledgers. Unfortunately, the production log sheet for last week has gone missing. However, from other documents he was able to figure out that [latex]1,250[/latex] units in total were produced last week. The production machinery was run for [latex]2,562.5[/latex] minutes, and he knows that Product A takes [latex]1.5[/latex] minutes to manufacture while Product B takes [latex]2.75[/latex] minutes to manufacture. How many units of each product were produced last week?
Solutions
- [latex]y=\$620.14[/latex]
- [latex]t=0.282211[/latex]
- [latex]\text{Delay}=1.5\;\text{hours}[/latex]
- [latex]\text{Users in 2000}=107,998,376[/latex]
- [latex]\text{Direct cost}=\$3,000[/latex]
- [latex]\text{Gross income}=\$140,000[/latex]
- [latex]\text{Single tickets}=10,363[/latex], [latex]\text{3-pack Tickets}=1,879[/latex]
- [latex]\text{A}=700\;\text{units}[/latex], [latex]\text{B}=550\;\text{units}[/latex]
Challenge, Critical Thinking, & Other Applications
- Jacob owns [latex]15,000[/latex] shares in a corporation, which represents [latex]2\%[/latex] of all issued shares for the company. He sold [latex]25[/latex] of his shares to another investor for [latex]\$7,800[/latex]. What is the total value for all of the shares issued by the company?
- Two cellphone companies are offering different rate plans. Rogers is offering [latex]\$19.99[/latex] per month, which includes a maximum of [latex]200[/latex] weekday minutes plus [latex]\$0.35[/latex] for every minute above the maximum. TELUS is offering [latex]\$39.99[/latex] for a maximum [latex]300[/latex] weekday minutes, but it charges [latex]\$0.10[/latex] for every minute above the maximum. Above how many minutes would TELUS be the better choice?
- Marianne, William, Hendrick, and Charlotte have all decided to go into business together. They need [latex]\$175,000[/latex] in initial capital funding. William was able to contribute [latex]20\%[/latex] less than Marianne, Hendrick contributed [latex]62.5\%[/latex] more than William, and Charlotte contributed [latex]\$5,000[/latex] less than half as much as Marianne. How much did each partner contribute to the initial funds?
- A mall is being constructed and needs to meet the legal requirements for parking availability. Parking laws require one parking stall for every [latex]100[/latex] square feet of retail space. The mall is designed to have [latex]1,200,000[/latex] square feet of retail space. Of the total parking stalls available, [latex]2\%[/latex] need to be handicap accessible, there need to be three times as many small car spaces as handicap spaces, RV spaces need to be one-quarter of the number of small car spaces, and the rest of the spaces are for regular stalls. How many of each type of parking space does the mall require?
- Simplify the following equation into the format of “[latex]z=[/latex]” and find the root. Verify the solution through substitution.
[latex]\begin{align*}z\left(1+0.073\times\frac{280}{365}\right)-\frac{z}{1+0.073\times\frac{74}{365}}+\$1,000=\$2,764.60\end{align*}[/latex]
- Find the roots for the following pair of equations. Verify the solution through substitution into both equations.
[latex]\begin{align*}3\frac{4}{5}q+0.18r&=12.2398\\[1ex]-5.13q-\frac{13r}{5}&=-38.4674\end{align*}[/latex]
Solutions
- [latex]\text{Company shares}=\$975,000[/latex]
- [latex]240\;\text{minutes}[/latex]
- [latex]\text{Marianne}=\$50,000[/latex]; [latex]\text{William}=\$40,000[/latex]; [latex]\text{Hendrick}=\$65,000[/latex]; [latex]\text{Charlotte}=\$20,000[/latex]
- [latex]\text{Regular stalls}=10,860[/latex]; [latex]\text{Handicap stalls}=240[/latex]; [latex]\text{Small car stalls}=720[/latex]; [latex]\text{RV stalls}=180[/latex]
- [latex]z=\$25,000[/latex]
- [latex]q=2.78[/latex]; [latex]r=9.31[/latex]
Attribution
“2.5 Linear Equations: Manipulating and Solving” from Business Math: A Step-by-Step Handbook (2021B) by J. Olivier and Lyryx Learning Inc. through a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License unless otherwise noted.

