5.1: Principal, Rate, Time

Introduction

Your investments may be at risk if stock and bond markets slump, as a story in the Globe and Mail predicts. You wonder if you should shift your money into relatively secure short-term investments until the market booms again. You consider your high-interest savings account, but realize that only the first [latex]\$60,000[/latex] of your savings account is insured. Perhaps you should put some of that money into treasury bills instead.

Looking ahead, what income will you live on once you are no longer working? As your career develops, you need to save money to fund your lifestyle in retirement. Some day you will have [latex]\$100,000[/latex] or more that you must invest and reinvest to reach your financial retirement goals.

To make such decisions, you must first understand how to calculate simple interest. Second, you need to understand the characteristics of the various financial options that use simple interest. Armed with this knowledge, you can make smart financial decisions!

The world of finance calculates interest in two different ways:

1. Simple Interest: A simple interest system primarily applies to short-term financial transactions, with a time frame of less than one year. In this system, which is explored in this chapter, interest accrues but does not compound.
2. Compound Interest: A compound interest system primarily applies to long-term financial transactions, with a time frame of one year or more. In this system, which the next chapter explores, interest accrues and compounds upon previously earned interest.

Simple Interest

In a simple interest environment, you calculate interest solely on the amount of money at the beginning of the transaction. When the term of the transaction ends, you add the amount of the simple interest to the initial amount. Therefore, throughout the entire transaction the amount of money placed into the account remains unchanged until the term expires. It is only on this date that the amount of money increases. Thus, an investor has more money or a borrower owes more money at the end.

The figure illustrates the concept of simple interest. In this example, assume [latex]\$1,000[/latex] is placed into an account with [latex]12\%[/latex] simple interest for a period of [latex]12[/latex] months. For the entire term of this transaction, the amount of money in the account always equals [latex]\$1,000[/latex]. During this period, interest accrues at a rate of [latex]12\%[/latex], but the interest is never placed into the account. When the transaction ends after [latex]12[/latex] months, the [latex]\$120[/latex] of interest and the initial [latex]\$1,000[/latex] are then combined to total [latex]\$1,120[/latex].

A loan or investment always involves two parties—one giving and one receiving. No matter which party you are in the transaction, the amount of interest remains unchanged. The only difference lies in whether you are earning or paying the interest.

• If you take out a personal loan from a bank, the bank gives you the money and you receive the money. In this situation, the bank earns the simple interest and you are being charged simple interest on your loan. In the figure, this means you must pay back not only the [latex]\$1,000[/latex] you borrowed initially but an additional [latex]\$120[/latex] in interest.
• If you place your money into an investment account at the bank, you have given the money and the bank has received the money. In this situation, you earn the simple interest on your money and the bank pays simple interest to your investment account. In the figure, this means the bank must give you back your initial [latex]\$1,000[/latex] at the end plus an additional [latex]\$120[/latex] of interest earned.

The best way to understand how simple interest is calculated is to think of the following relationship:

[latex]\text{Amount of Interest}=\underbrace{\text{How Much}}\text{ at }\underbrace{\text{What Simple Interest Rate}}\text{ for }\underbrace{\text{How Long}}[/latex]

Notice that the key variables are the amount, the simple interest rate, and time. Formula 5.1 combines these elements into a formula for simple interest.

[latex]\boxed{5.1}[/latex] Simple Interest

[latex]\color{red}{I\;}\color{black}{\text{is Interest Amount:}}[/latex] The interest amount is the dollar amount of interest that is paid or earned. To interpret the interest amount properly, remember who you are in the transaction. If you are borrowing the money, this is the interest amount charged to you. If you are investing the money, this is the interest amount you earn.

[latex]\color{blue}{P\;}\color{black}{\text{is Present Value or Principal:}}[/latex] The amount of money at the beginning of the time period being analyzed is known as the present value, or [latex]P[/latex]. If this is in fact the amount at the start of the financial transaction, it is also called the principal, which is the original amount of money that is borrowed or invested. Or it can simply be the amount at some earlier time before the future value was known. In any case, the amount excludes the interest.

[latex]\color{purple}{t}\color{black}{\;\text{is Time:}}[/latex] The time period or term is the length of the financial transaction for which interest is charged or earned.

[latex]\color{green}r\;{\color{black}{\text{is Interest Rate:}}}[/latex] The interest rate is the rate of interest that is charged or earned during a specified time period. It is usually expressed in percent format. Unless noted otherwise, interest rates are expressed on an annual basis. An interest rate is the result of Formula 3.1b[latex]\begin{align*}\text{Rate}=\frac{\text{Portion}}{\text{Base}}\end{align*}[/latex], where:

[latex]\begin{align*}\text{Rate}=\frac{\text{Portion}}{\text{Base}}\end{align*}[/latex]

In this case, you calculate an annual interest rate in its decimal format as follows:

[latex]\begin{align*}\text{Annual Interest Rate}=\frac{\text{Annual Interest Amount}}{\text{Principal}}\end{align*}[/latex]

Thus, if you are earning [latex]\$3[/latex] of interest annually on a [latex]\$100[/latex] principal, then your annual interest rate is [latex]\frac{3}{100}=0.03[/latex] or [latex]3\%[/latex].

Assume you have [latex]\$500[/latex] earning [latex]3\%[/latex] simple interest for a period of nine months. How much interest do you earn?

Step 1: Note that your principal is [latex]\$500[/latex], or [latex]P=\$500[/latex]. The interest rate is assumed to be annual, so [latex]r=3\%[/latex] per year. The time period is nine months.

Step 2: Convert the time period from months to years: [latex]t=\frac{9}{12}[/latex].

Step 3: According to Formula 5.1:

[latex]\begin{eqnarray*}I&=&Prt\\I&=&\$500\times3\%\times\frac9{12}\\I&=&\$11.25\end{eqnarray*}[/latex]

Therefore, the amount of interest you earn on the [latex]\$500[/latex] investment over the course of nine months is [latex]\$11.25[/latex].

  Paths To Success

Four variables are involved in the simple interest formula, which means that any three can be known, requiring you to solve for the fourth missing variable. To reduce formula clutter, the triangle technique illustrated in the video helps you remember how to rearrange the formula as needed.

Example 5.1.1

Julio borrowed [latex]\$1,100[/latex] from Maria five months ago. When he first borrowed the money, they agreed that he would pay Maria [latex]5\%[/latex] simple interest. If Julio pays her back today, how much interest does he owe her?

Solution

Step 1: What are we looking for?

You need to calculate the amount of interest that Julio owes Maria.

Step 2: What do we already know?

The terms of their agreement are as follows:

[latex]P=\$1,100[/latex]           [latex]r=5\%[/latex]                  [latex]t=5\;\text{months}[/latex]

Step 3: Make substitutions using the information known above.

The rate is annual, and the time is in months. Convert the time to an annual number. Since five months out of [latex]12[/latex] months in a year is [latex]\frac{5}{12}[/latex] of a year, [latex]t=\frac{5}{12}[/latex].

 

Apply Formula 5.1[latex]I=Prt[/latex].

[latex]\begin{eqnarray*}I&=&\$1,100\times5\%\times\frac5{12}\\[1ex]I&=&\$1,100\times0.05\times\frac5{12}\\[1ex]I&=&\$22.92\end{eqnarray*}[/latex]

Step 4: Provide the information in a worded statement.

For Julio to pay back Maria, he must reimburse her for the [latex]\$1,100[/latex] principal borrowed plus an additional [latex]\$22.92[/latex] of simple interest as per their agreement.

Example 5.1.2

A [latex]\$3,500[/latex] investment earned [latex]\$70[/latex] of interest over the course of six months. What annual rate of simple interest did the investment earn?

Solution

Step 1: What are we looking for?

You need to calculate the annual interest rate ([latex]r[/latex]).

Step 2: What do we already know?

The principal, interest amount, and time are known:

[latex]P=\$3,500[/latex]           [latex]I=\$70[/latex]                  [latex]t=6\;\text{months}[/latex]

Step 3: Make substitutions using the information known above.

The computed interest rate needs to be annual, so you must express the time period annually as well. Since six months out of [latex]12[/latex] months in a year is [latex]\frac{6}{12}[/latex] of a year, [latex]t=\frac{6}{12}[/latex].

 

Apply Formula 5.1[latex]I=Prt[/latex], rearranging for [latex]r[/latex].

[latex]\begin{eqnarray*}\$70&=&\$3,500\times r\times\frac6{12}\\[1ex]r&=&\frac{\$70}{\$3,500\times\frac6{12}}\\[1ex]r&=&\frac{\$70}{\$1,750}\\[1ex]r&=&0.04\;\text{or}\;4\%\end{eqnarray*}[/latex]

Step 4: Provide the information in a worded statement.

For [latex]\$3,500[/latex] to earn [latex]\$70[/latex] simple interest over the course of six months, the annual simple interest rate must be [latex]4\%[/latex].

Example 5.1.4

For how many months must [latex]\$95,000[/latex] be invested to earn [latex]\$1,187.50[/latex] of simple interest at an interest rate of [latex]5\%[/latex]?

Solution

Step 1: What are we looking for?

You need to calculate the length of time in months ([latex]t[/latex]) that it takes the money to acquire the interest.

Step 2: What do we already know?

The amount of money invested, interest earned, and interest rate are known:

[latex]P=\$95,000.00[/latex]       [latex]I=\$1,187.50[/latex]       [latex]r=5\%[/latex]

Step 3: Make substitutions using the information known above.

Express the time in months. Convert the interest rate to a “per month” format. [latex]5\%[/latex] per year converted into a monthly rate is [latex]r=\frac{0.05}{12}[/latex].

 

Apply Formula 5.1[latex]I=Prt[/latex], rearranging for [latex]t[/latex].

[latex]\begin{eqnarray*}\$1,187.50&=&\$95,000\times\frac{0.05}{12}\times t\\[1ex]t&=&\frac{\$1,187.50}{\$95,000\times\frac{0.05}{12}}\\[1ex]t&=&\frac{\$1,187.50}{\$95,000\times0.00416}\\[1ex]t&=&3\;\text{months}\end{eqnarray*}[/latex]

Step 4: Provide the information in a worded statement.

For [latex]\$95,000[/latex] to earn [latex]\$1,187.50[/latex] at [latex]5\%[/latex] simple interest, it must be invested for a three-month period.

Time and Dates

In the examples of simple interest so far, the time period was given in months. While this is convenient in many situations, financial institutions and organizations calculate interest based on the exact number of days in the transaction, which changes the interest amount.
To illustrate this, assume you had money saved for the entire months of July and August, where [latex]t = \frac{2}{12}[/latex] or [latex]t = 0.16666...=0.1\overline{6}[/latex] of a year. However, if you use the exact number of days, the [latex]31[/latex] days in July and [latex]31[/latex] days in August total [latex]62[/latex] days. In a [latex]365[/latex]-day year that is [latex]t=\frac{62}{365}[/latex] or [latex]t=0.169863[/latex] of a year. Notice a difference of [latex]0.003196[/latex] ([latex]0.169863-0.16[/latex]) occurs. Therefore, to be precise in performing simple interest calculations, you must calculate the exact number of days involved in the transaction.

Using The BA 2+ Plus Date Function to Calculate the Exact Number of Days

In the video below we’ll demonstrate how to use the BA2+ Date Function:

Example 5.1.5

On September 13, 2011, Aladdin decided to pay back the Genie on his loan of [latex]\$15,000[/latex] at [latex]9\%[/latex] simple interest. If he paid the Genie the principal plus [latex]\$1,283.42[/latex] of interest, on what day did he borrow the money from the Genie?

Solution

Step 1: Given variables:

[latex]P=\$15,000[/latex];        [latex]I=\$1,283.42[/latex];        [latex]r=9\%\;\text{per year}[/latex];        [latex]\text{End Date}=\text{September 13, 2011}[/latex]

Step 2: The time is in days, but the rate is annual. Convert the rate to a daily rate:

[latex]\begin{align*}r=\frac{9\%}{365}\end{align*}[/latex]

Step 3: Solve for the time, [latex]t[/latex].

[latex]\begin{eqnarray}t&=&\frac I{Pr}\\[1ex]t&=&\frac{\$1,\!283.42}{\$15,\!000\times\frac{0.09}{365}}\\[1ex]t&=&346.998741=347\;\text{days}\end{eqnarray}[/latex]

Step 4: Use the DATE function to calculate the start date (DT1). Use the time in days.

Calculator Instructions:

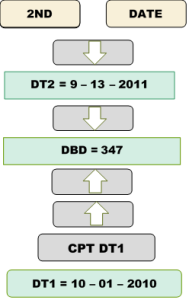
Step 5: Write as a statement.

If Aladdin owed the Genie [latex]\$1,283.42[/latex] of simple interest at [latex]9\%[/latex] on a principal of [latex]\$15,000[/latex], he must have borrowed the money [latex]347[/latex] days earlier, which is October 1, 2010.

Section 5.1 Exercises