2.5: Algebraic Expressions
The Pieces of the Puzzle
If you are like most Canadians, your employer pays you biweekly. Assume you earn [latex]$12.00[/latex] per hour. How do you calculate your pay cheque every pay period? Your earnings are calculated as follows:
[latex]\$12.00\times(\text{Hours worked during the biweekly pay period})[/latex]
The hours worked during the biweekly pay period is the unknown variable. Notice that the expression appears lengthy when you write out the explanation for the variable. Algebra is a way of making such expressions more convenient to manipulate. To shorten the expression, making it easier to read, algebra assigns a letter or group of letters to represent the variable. In this case, you might choose [latex]h[/latex] to represent “hours worked during the biweekly pay period.” This rewrites the above expression as follows:
[latex]\$12.00\times h\;\text{or}\;\$12h[/latex]
Unfortunately, the word algebra makes many people’s eyes glaze over. But remember that algebra is just a way of solving a numerical problem. It demonstrates how the pieces of a puzzle fit together to arrive at a solution.
For example, you have used your algebraic skills if you have ever programmed a formula into Microsoft Excel. You told Excel there was a relationship between cells in your spreadsheet. Perhaps your calculation required cell A3 to be divided by cell B6 and then multiplied by cell F2. This is an algebraic equation. Excel then took your algebraic equation and calculated a solution by automatically substituting in the appropriate values from the referenced cells (your variables).
As illustrated in the figure above, algebra involves integrating many interrelated concepts. This figure shows only the concepts that are important to business mathematics, which this textbook will present piece by piece. Your understanding of algebra will become more complete as more concepts are covered over the course of this book.
This section reviews the language of algebra, exponent rules, basic operation rules, and substitution. In Section 2.6 you will put these concepts to work in solving one linear equation for one unknown variable along with two linear equations with two unknown variables.
The Language of Algebra
Understanding the rules of algebra requires familiarity with four key definitions.
Algebraic Expression
A mathematical algebraic expression indicates the relationship between mathematical operations that must be conducted on a series of numbers or variables. For example, the expression [latex]\$12h[/latex] says that you must take the hourly wage of [latex]\$12[/latex] and multiply it by the hours worked. Note that the expression does not include an equal sign, or “[latex]=[/latex]“. It only tells you what to do and requires that you substitute a value in for the unknown variable(s) to solve. There is no one definable solution to the expression.
Algebraic Equation
A mathematical algebraic equation takes two algebraic expressions and equates them. This equation can be solved to find a solution for the unknown variables. Examine the equation above to see how algebraic expressions and algebraic equations are interrelated.
[latex]{\color{red}{6x+3y}}\text{ is the First Algebraic Expression:}[/latex] This expression on the left-hand side of the equation expresses a relationship between the variables [latex]x[/latex] and [latex]y[/latex]. By itself, any value can be substituted for [latex]x[/latex] and [latex]y[/latex] and any solution can be calculated.
[latex]{\color{blue}{4x+3}}\text{ is the Second Algebraic Expression:}[/latex] This expression on the right-hand side of the equation expresses a relationship between [latex]x[/latex] and a number. By itself, any value can be substituted for [latex]x[/latex] and any solution can be generated.
[latex]{\color{green}{=}}\text{ is the Equality:}[/latex] By having the equal sign placed in between the two algebraic expressions, they now become an algebraic equation. Now there would be a particular value for [latex]x[/latex] and a particular value for y that makes both expressions equal to each other (try [latex]x = −0.75[/latex] and [latex]y = 1.125[/latex]).
Term
In any algebraic expression, terms are the components that are separated by addition and subtraction. In looking at the example above, the expression [latex]6x + 3y[/latex] is composed of two terms. These terms are “[latex]6x[/latex]” and “[latex]3y[/latex]”. A nomial refers to how many terms appear in an algebraic expression. If an algebraic expression contains only one term, like “[latex]\$12.00h[/latex],” it is called a monomial. If the expression contains two terms or more, such as “[latex]6x + 3y[/latex],” it is called a polynomial.
Factor
Terms may consist of one or more factors that are separated by multiplication or division signs. Using the [latex]6x[/latex] from above, it consists of two factors. These factors are “[latex]6[/latex]” and “[latex]x[/latex]”; they are joined by multiplication.
- If the factor is numerical, it is called the numerical coefficient.
- If the factor is one or more variables, it is called the literal coefficient.
The equation and info below shows how algebraic expressions, algebraic equations, terms, and factors all interrelate within an equation.
[latex]{\color{red}{\frac{7x}3}}\text{ First Term:}[/latex] This term consists of two factors, where the numerical coefficient is [latex]\frac73[/latex] and the literal coefficient is [latex]x[/latex].
[latex]\underbrace{{\color{red}{\frac{7x}3}}+{\color{blue}{4xy^2}}}\text{ First Algebraic Expression:}[/latex] This first polynomial expression is composed of the two terms [latex]\frac{7x}3[/latex] and [latex]4xy^2[/latex].
[latex]{\color{blue}{4xy^2}}\text{ Second Term:}[/latex] This term consists of three factors where the numerical coefficient is [latex]4[/latex] and the literal coefficients are [latex]x[/latex] and [latex]y^2[/latex].
[latex]{\color{green}{=}}\text{ Equal Sign:}[/latex] The equal sign joins the two algebraic expressions, turning this into an algebraic equation.
[latex]\underbrace{{\color{magenta}{x^3}}{\color{chocolate}{-2y}}}\text{ Second Algebraic Expression:}[/latex] This second polynomial expression consists of the two terms [latex]x^3[/latex] and [latex]−2y[/latex].
[latex]{\color{magenta}{x^3}}\text{ First Term:}[/latex] This term consists of two factors, which are the literal coefficient [latex]x^3[/latex] and a numerical coefficient of [latex]1[/latex] (recall that in math you do not write the [latex]1[/latex] when writing [latex]1x^3[/latex] since it doesn’t change anything).
[latex]{\color{chocolate}{-2y}}\text{ Second Term:}[/latex] This term consists of two factors, where the numerical coefficient is [latex]−2[/latex] and the literal coefficient is [latex]y[/latex].
Exponents
Exponents are widely used in business mathematics and are integral to financial mathematics. When applying compounding interest rates to any investment or loan, you must use exponents. Exponents are a mathematical shorthand notation that indicates how many times a quantity is multiplied by itself. The format of an exponent is illustrated below.
[latex]{\color{blue}{\text{Base}}}\text{ is the quantity:}[/latex] This is the quantity that is to be multiplied by itself.
[latex]{\color{red}{\text{Exponent}}}\text{ is the multiplication factor:}[/latex] This is the number that indicates how many times the base is to be multiplied by itself.
[latex]{\color{green}{\text{Power}}}\text{ s the product:}[/latex] This is the result of performing the multiplication indicated, or the answer.
Assume you have [latex]2^3= 8[/latex]. The exponent of [latex]3[/latex] says to take the base of [latex]2[/latex] multiplied by itself three times, or [latex]2 \times 2 \times 2[/latex]. The power is [latex]8[/latex]. The proper way to state this expression is “2 to the exponent of 3 results in a power of 8.”
HOW TO
Simplify Exponents
Apply the rules for simplifying exponents as shown in the table below.
| Rule | Formula | Explanation |
|---|---|---|
| 1. Multiplication | [latex]y^a\times y^b=y^{a+b}[/latex] | If the bases are identical, add the exponents and retain the unchanged base. |
| 2. Division | [latex]\frac{y^a}{y^b}=y^{a-b}[/latex] | If the bases are identical, subtract the exponents and retain the unchanged base. |
| 3. Raising powers to exponents | [latex]\begin{eqnarray*}{(y^bz^c)}^a&=&y^{b\times a}z^{c\times a}\\&\text{or}\\\left(\frac{y^b}{z^c}\right)^a&=&\frac{y^{b\times a}}{z^{c\times a}}\\\end{eqnarray*}[/latex] | If a single term is raised to an exponent, each factor must retain its base and you must multiply the exponents for each by the raised exponent. Note that if the expression inside the brackets has more than one term, such as [latex](y^b+z^c)^a[/latex], which has two terms, you cannot multiply the exponent a inside the brackets. |
| 4. Zero exponents | [latex]y^0= 1[/latex] | Any base to a zero exponent will always produce a power of [latex]1[/latex]. This is explained later in this section when you review the concept of algebraic division. |
| 5. Negative exponents | [latex]y^{-a}=\frac1{y^a}[/latex] | The negative sign indicates that the power has been shifted between the numerator and denominator. It is commonly used in this textbook to simplify appearances. Note that on the BAII Plus calculator, keying in a negative exponent requires you to key in the value of [latex]y[/latex], press [latex]y^x[/latex], enter the value of a, press [latex]\pm[/latex], and then press [latex]=[/latex] to calculate. |
| 6. Fractional exponents | [latex]y^\frac ab=\sqrt[b]{y^a}[/latex] | A fractional exponent is a different way of writing a radical sign. Note that the base is first taken to the exponent of a, then the root of b is found to get the power. For example, [latex]2^{\frac{4}{2}}=\sqrt[2]{2^4}=\sqrt[2]{16}=4[/latex]. This is the same as [latex]2^{\frac{4}{2}}=2^2=4[/latex]. To key in a fractional exponent on the BAII Plus calculator, input the value of [latex]y[/latex], press [latex]y^x[/latex], open a set of brackets, key in [latex]a \divsymbol b[/latex], close the brackets, and press [latex]=[/latex] to calculate. |
 Key Takeaway
Key Takeaway
Example 2.5.1
Simplify the following expressions:
- [latex]h^3\times h^6[/latex]
- [latex]\begin{align*}\frac{h^{14}}{h^8}\end{align*}[/latex]
- [latex]\begin{align*}\left[\frac{hk^5m^3}{n^4}\right]^3\end{align*}[/latex]
- [latex]1.49268^0[/latex]
- [latex]\begin{align*}\frac{x^2y^4}{xy^{-2}}\end{align*}[/latex]
- [latex]\begin{align*}6^\frac35\end{align*}[/latex]
Solution
a.
Step 1: Figure out the rule needed from the table above to answer the question.
This expression involves multiplying two powers with the same base.
Apply Rule #1
Step 2: Solve using Rule #1 – Multiplication.
[latex]\begin{eqnarray*}&=&h^3\times h^6\\&=&h^{3+6}\\&=&h^9\end{eqnarray*}[/latex]
b.
Step 1: Figure out the rule needed from the table above to answer the question.
This expression involves dividing two powers with the same base.
Apply Rule #2
Step 2: Solve using Rule #2 – Division.
[latex]\begin{eqnarray*}&=&\frac{h^{14}}{h^8}\\[1ex]&=&h^{14-8}\\&=&h^6\end{eqnarray*}[/latex]
c.
Step 1: Figure out the rule needed from the table above to answer the question.
This expression involves a single term, with products and a quotient all raised to an
exponent.
Apply Rule #3
Step 2: Solve using Rule #3 – Raising Powers to Exponents.
[latex]\begin{eqnarray*}&=&\left[\frac{hk^5m^3}{n^4}\right]^3\\[1ex]&=&\frac{h^{1\times3}k^{5\times3}m^{3\times3}}{n^{4\times3}}\\[1ex]&=&\frac{h^3k^{15}m^9}{n^{12}}\end{eqnarray*}[/latex]
d.
Step 1: Figure out the rule needed from the table above to answer the question.
This power involves a zero exponent.
Apply Rule #4
Step 2: Solve using Rule #4 – Zero exponents.
[latex]1.49268^0=1[/latex]
e.
Step 1: Figure out the rule needed from the table above to answer the question.
This expression involves multiplication, division, and negative exponents.
Apply Rules #1, #2, and #5
Step 2: Solve using Rule #1, #2, #5 – Multiplication, Division and Negative exponents
[latex]\begin{eqnarray*}&=&\frac{x^2y^4}{xy^{-2}}\\[1ex]&=&\;\frac{x^2y^4y^2}{x^1}\;\text{Rule #5}\\[1ex]&=&\frac{x^2y^{4+2}}{x^1}\;\text{Rule #1}\\[1ex]&=&\frac{x^2y^6}{x^1}\\[1ex]&=&x^{2-1}y^6\;\text{Rule #2}\\[1ex]&=&xy^6\end{eqnarray*}[/latex]
f.
Step 1: Figure out the rule needed from the table above to answer the question.
This power involves a fractional exponent.
Apply Rule #6
Step 2: Solve using Rule #6 – Fractional Exponents.
[latex]\begin{eqnarray*}&=&6^\frac35\\&=&2.930156\end{eqnarray*}[/latex]
Addition and Subtraction
Simplification of unnecessarily long or complex algebraic expressions is always preferable to increase understanding and reduce the chances of error. For example, assume you are a production manager looking to order bolts for a product that you make. Your company makes three products, all in equal quantity. Product A requires seven bolts, Product B requires four bolts, and Product C requires fourteen bolts. If [latex]q[/latex] represents the quantity of products required, you need to order [latex]7q + 4q + 14q[/latex] bolts. This expression requires four calculations to solve every time (each term needs to be multiplied by [latex]q[/latex] and you then need to add everything together). With the algebra rules that follow, you can simplify this expression to [latex]25q[/latex]. This requires only one calculation to solve. So what are the rules?
HOW TO
Add or Subtract like terms
In math, terms with the same literal coefficients are called like terms. Only terms with the identical literal coefficients may be added or subtracted through the following procedure:
Step 1: Simplify any numerical coefficients by performing any needed mathematical operation or converting fractions to decimals.
For example, terms such as [latex]\frac12y[/latex] should become [latex]0.5y[/latex].
Step 2: Add or subtract the numerical coefficients of like terms as indicated by the operation while obeying the rules of BEDMAS.
Step 3: Retain and do not change the common literal coefficients. Write the new numerical coefficient in front of the retained literal coefficients.
From the previous example, you require [latex]7q + 4q + 14q[/latex] bolts. Notice that there are three terms, each of which has the same literal coefficient. Therefore, you can perform the required addition.
Step 1: All numerical coefficients are simplified already. Skip to Step 2.
Step 2: Take the numerical coefficients and add the numbers: [latex]7 + 4 + 14[/latex] equals [latex]25[/latex].
Step 3: Retain the literal coefficient of [latex]q[/latex]. Put the new numerical coefficient and literal coefficient together. Thus, [latex]25q[/latex]. Therefore [latex]7q + 4q + 14q[/latex] is the same as [latex]25q[/latex].
Things To Watch Out For
A common mistake in addition and subtraction is combining terms that do not have the same literal coefficient. You need to remember that the literal coefficient must be identical. For example, [latex]7q[/latex] and [latex]4q[/latex] have the identical literal coefficient of [latex]q[/latex]. However, [latex]7q[/latex] and [latex]4q^2[/latex] have different literal coefficients, [latex]q[/latex] and [latex]q^2[/latex], and cannot be added or subtracted.
 Paths To Success
Paths To Success
Remember that if you come across a literal coefficient with no number in front of it, that number is assumed to be a [latex]1[/latex]. For example, [latex]x[/latex] has no written numerical coefficient, but it is the same as [latex]1x[/latex]. Another example would be [latex]\frac x4[/latex] is the same as [latex]\frac{1x}4[/latex] or [latex]\frac14x[/latex]. On a similar note, mathematicians also don’t write out literal coefficients that have an exponent of zero. For example, [latex]7x^0 [/latex]is just [latex]7(1)[/latex] or [latex]7[/latex]. Thus, the literal coefficient is always there; however, it has an exponent of zero. Remembering this will help you later when you multiply and divide in algebra.
Try it
1) Examine the following algebraic expressions and indicate how many terms can be combined through addition and subtraction. No calculations are necessary. Do not attempt to simplify.
- [latex]32x+4x^2-10x-2y+x^3[/latex]
- [latex]23g^2-17g^25+g^4+g^2-23g^2-0.15g+g^3[/latex]
Solution
- Three terms (all of the [latex]x[/latex])
- Four terms (all of the [latex]g^2[/latex])
Example 2.5.2
Simplify the following three algebraic expressions.
- [latex]9x+3y-\frac72x+4y[/latex]
- [latex]P\left(1+0.11\times\frac{121}{365}\right)+\frac{15P}{1+0.11\times{\displaystyle\frac{36}{365}}}[/latex]
- [latex]x\left(1+\frac{0.1}4\right)^3+\frac x{\left(1+{\displaystyle\frac{0.1}4}\right)^4}-\frac{3x}{\left(1+{\displaystyle\frac{0.1}4}\right)^2}[/latex]
Solution
a.
Step 1: Simplify the numerical coefficients.
Eliminate the fraction.
[latex]9x+3y-{\color{red}{3.5}}x+4y[/latex]
Step 2: Combine the numerical coefficients of like terms and solve.
You have two terms with [latex]x[/latex] and two terms with [latex]y[/latex] from which you need combine and simplify.
[latex]\begin{eqnarray*}&=&{\color{red}{9x}}+{\color{blue}{3y}}{\color{red}{\;-\;3.5x}}+{\color{blue}{4y}}\\&=&({\color{red}{9x-3.5x}})+({\color{blue}{3y+4y}})\\&=&{\color{red}{5.5x}}+{\color{blue}{7y}}\end{eqnarray*}[/latex]
Step 3: Write as a statement.
The simplified expression is [latex]5.5x\;+7y[/latex].
b.
Step 1: Simplify the numerical coefficients.
Eliminate the first fraction.
[latex]\begin{align*}({\color{red}{1.036465}})P+{\color{blue}{\frac{15}{1.010849}}}P\end{align*}[/latex]
Step 2: Continue to simplify the second term.
Eliminate the second fraction.
[latex]{\color{red}{1.036465}}P+{\color{blue}{14.839006}}P[/latex]
Step 3: Combine the numerical coefficients by performing addition.
Rewrite the numerical coefficient in front of the unchanged literal coefficient.
[latex]15.875472P[/latex]
Step 4: Write as a statement.
The simplified expression is [latex]15.875472P[/latex].
c.
Step 1: Simplify the numerical coefficients.
Eliminate the first fraction.
[latex]\begin{align*}{\color{red}{1.076890}}x+{\color{blue}{\frac1{1.103812}}}x-{\color{green}{\frac3{1.050625}}}x\end{align*}[/latex]
Step 2: Continue to simplify the second term.
Eliminate the second fraction.
[latex]\begin{align*}{\color{red}{1.076890}}x+{\color{blue}{0.905950}}x-{\color{green}{\frac3{1.050625}}}x\end{align*}[/latex]
Step 3: Complete the last simplification.
Eliminate the third fraction.
[latex]{\color{red}{1.076890}}x+{\color{blue}{0.905950}}x-{\color{green}{2.855443}}x[/latex]
Step 4: Combine and solve the numerical coefficients through the specified operation.
[latex]\begin{eqnarray*}&=&1.98284x-2.855443x\\&=&-0.872603x\end{eqnarray*}[/latex]
Step 5: Write as a statement.
The simplified expression is [latex]-0.872603x[/latex].
Notice how much easier these are to work with than the original expressions.
Multiplication
Whether you are multiplying a monomial by another monomial, a monomial by a polynomial, or a polynomial by another polynomial, the rules for multiplication remain the same.
HOW TO
Solve multiple algebraic expressions
Step 1: Check to see if there is any way to simplify the algebraic expression first. Are there any like terms you can combine?
For example, you can simplify [latex](3x+2+1)(x+x+4)[/latex] to [latex](3x+3)(2x+4)[/latex] before attempting the multiplication.
Step 2: Take every term in the first algebraic expression and multiply it by every term in the second algebraic expression. This means that numerical coefficients in both terms are multiplied by each other, and the literal coefficients in both terms are multiplied by each other. It is best to work methodically from left to right so that you do not miss anything. Working with the example, in [latex](3x+3)(2x+4)[/latex] take the first term of the first expression, [latex]3x[/latex], and multiply it by [latex]2x[/latex] and then by [latex]4[/latex]. Then move to the second term of the first expression, [latex]3[/latex], and multiply it by [latex]2x[/latex] and then by [latex]4[/latex] (See Figure 2.5.2).
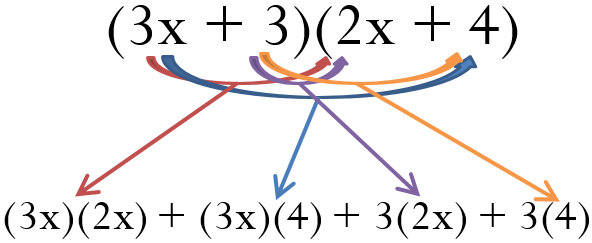
It becomes: [latex]6x^2 + 12x + 6x + 12[/latex]
Step 3: Perform any final steps of simplification by adding or subtracting like terms as needed. In the example, two terms contain the literal coefficient [latex]x[/latex], so you simplify the expression to [latex]6x^2 + 18x + 12[/latex].
 Key Takeaway
Key Takeaway
If the multiplication involves more than two expressions being multiplied by each other, it is easiest to work with only one pair of expressions at a time starting with the leftmost pair. For example, if you are multiplying [latex](4x + 3)(3x)(9y + 5x)[/latex], resolve [latex](4x + 3)(3x)[/latex] first. Then take the solution, keeping it in brackets since you have not completed the math operation, and multiply it by [latex](9y + 5x)[/latex]. This means you are required to repeat Step 2 in the multiplication procedure until you have resolved all the multiplications.
Things To Watch Out For
The negative sign causes no end of grief for a lot of people when working with multiplication. First, if a numerical coefficient is not written explicitly, it is assumed to be [latex]1[/latex].
For example, look at [latex]2(4a + 6b) − (2a − 3b)[/latex]. This is the same as [latex]2(4a + 6b) + (−1)(2a − 3b)[/latex].
When you multiply a negative through an expression, all signs in the brackets will change.
Continuing with the second term in the above example, [latex]−(2a − 3b)[/latex] becomes [latex]−2a + 3b[/latex]. The expression then looks like [latex]2(4a + 6b) − 2a + 3b[/latex].
 Paths To Success
Paths To Success
The order in which you write the terms of an algebraic expression does not matter so long as you follow all the rules of BEDMAS. For example, whether you write [latex]3 \times 4[/latex] or [latex]4 \times 3[/latex], the answer is the same because you can do multiplication in any order. The same applies to [latex]4 + 3 - 1[/latex] or [latex]3 - 1 + 4[/latex]. Now let’s get more complex. Whether you write [latex]3x^2 + 5x 4[/latex] or [latex]5x 4 + 3x^2[/latex], the answer is the same as you have not violated any rules of BEDMAS. You still multiply first and add last from left to right.
Although the descending exponential format for writing expressions is generally preferred, for example, [latex]3x^2 + 5x + 4[/latex], which lists literal coefficients with higher exponents first, it does not matter if you do this or not. When checking your solutions against those given in this textbook, you only need to ensure that each of your terms matches the terms in the solution provided.
Example 2.5.3
Simplify the following algebraic expression: [latex](6x+2+2)(3x–2)[/latex]
Solution
Step 1: Simplify the expression.
[latex](6x+{\color{red}{4}})(3x-2)[/latex]
Step 2: Multiply all terms in each expression with all the terms in the other expression.
[latex](6x)(3x)+(6x)(-2)+(4)(3x)+(4)(-2)[/latex]
Step 3: Resolve the multiplication.
[latex]18x^2-12x+12x-8[/latex]
Step 4: Perform final simplification.
[latex]18x^2-8[/latex]
Step 5: Write as a final statement.
The simplified algebraic expression is [latex]18x^2-8[/latex].
Example 2.5.4
Simplify the following algebraic expression: [latex]–(3ab)(a^2 + 4b – 2a) – 4(3a + 6)[/latex]
Solution
Step 1: Simplify.
You cannot simplify anything. Be careful with the negatives and write them out.
[latex]({\color{red}{-1}})(3ab)(a^2+4b-2a)+({\color{red}{-4}})(3a+6)[/latex]
Step 2: Work with the first pair of expressions in the first term and multiply.
[latex]({\color{red}{-3ab}})(a^2+4b-2a)+(-4)(3a+6)[/latex]
Step 3: Multiply the resulting pair of expressions in the first term.
[latex]{\color{red}{-3a^3b-12ab^2+6a^2b}}+(-4)(3a+6)[/latex]
Step 4: Work with the pair of expressions in the original second term and multiply.
[latex]-3a^3b-12ab^2+6a^2b+\lbrack{\color{blue}{-12a-24}}\rbrack[/latex]
Step 5: Drop the brackets to simplify.
[latex]-3a^3b-12ab^2+6a^2b+-12a-24[/latex]
Step 6: There are no like terms. You cannot simplify this expression any further.
Step 7: Write a statement.
The simplified algebraic expression is [latex]-3a^3b-12ab^2+6a^2b+-12a-24[/latex].
Division
You are often required to divide a monomial into either a monomial or a polynomial. In instances where the denominator consists of a polynomial, it is either not possible or extremely difficult to simplify the expression algebraically. Only division where denominators are monomials are discussed here.
HOW TO
Simplify an expression when its denominator is a monomial
Step 1: Just as in multiplication, determine if there is any way to combine like terms before completing the division.
For example, with:
[latex]\begin{align*}\frac{3ab+3ab-3a^2b+9ab^2}{3ab}\end{align*}[/latex]
you can simplify the numerator to:
[latex]\begin{align*}\frac{6ab-3a^2b+9ab^2}{3ab}\end{align*}[/latex].
Step 2: Take every term in the numerator and divide it by the term in the denominator. This means that you must divide both the numerical and the literal coefficients. As with multiplication, it is usually best to work methodically from left to right so that you do not miss anything.
So in our example we get:
[latex]\begin{eqnarray*}&=&\frac{6\cancel{ab}}{3\cancel{ab}}-\frac{3{\color{red}{a}}^\cancel2\cancel b}{3\cancel{ab}}+\frac{9\cancel a{\color{blue}{b}}^\cancel2}{3\cancel{ab}}\\&=&2\;-1{\color{red}{a}}+3{\color{blue}{b}}\\&=&\;2-a+3b\\\end{eqnarray*}[/latex]
Step 3: Perform any final simplification by adding or subtracting the like terms as needed.
As there are no more like terms, the final expression remains [latex]2−a+3b[/latex].
Things To Watch Out For
You may have heard of an outcome called “cancelling each other out.” For example, in resolving the division [latex]\frac{4a}{4a}[/latex] many people would say that the terms cancel each other out. Many people will also mistakenly interpret this to mean that the quotient is zero and say that [latex]\frac{4a}{4a}=0[/latex]. In fact, when terms cancel each other out the quotient is one, not zero. The numerical coefficient is [latex]\frac{4}{4}=1[/latex]. The literal coefficient is [latex]\frac{a}{a}=1[/latex]. Thus, [latex]\frac{4a}{4a}=\frac11=1[/latex]. This also explains why a zero exponent equals one: [latex]\frac{a^1}{a^1}=a^{1-1}=a^0=1[/latex].
 Paths To Success
Paths To Success
A lot of people dislike fractions and find them hard to work with. Remember that when you are simplifying any algebraic expression you can transform any fraction into a decimal. For example, if your expression is [latex]\frac{2x}5+\frac{3x}4[/latex], you can convert the fraction into decimals: [latex]0.4x+0.75x[/latex]. In this format, it is easier to solve.
Example 2.5.5
Simplify the following algebraic expression: [latex]\begin{align*}\frac{30x^6+5x^3+10x^3}{5x}\end{align*}[/latex]
Solution
Step 1: The numerator has two terms with the same literal coefficient ([latex]x^3[/latex]).
Combine these using the rules of addition.
[latex]\begin{align*}\frac{30x^6+{\color{red}{15x^3}}}{5x}\end{align*}[/latex]
Step 2: Now that the numerator is simplified, divide each of its terms by the denominator.
[latex]\begin{align*}\frac{30x^6}{5x}+\;\frac{{\color{red}{15x^3}}}{5x}\end{align*}[/latex]
Step 3: Resolve the divisions by dividing both numerical and literal coefficients.
[latex]\begin{eqnarray*}&=&\frac{30x^{\cancel6^5}}{5\cancel x}+\;\frac{15x^{\cancel3^2}}{5\cancel x}\\[1ex]&=&6x^5+3x^2\end{eqnarray*}[/latex]
Step 4: There are no like terms, so this is the final solution.
Step 5: Write a statement.
The simplified algebraic expression is [latex]6x^5+3x^2[/latex].
Example 2.5.6
Simplify the following algebraic expression: [latex]\begin{align*}\frac{15x^2y^3+25xy^2-xy+10x^4y+5xy^2}{5xy}\end{align*}[/latex]
Solution
Step 1: The numerator has two terms with the same literal coefficient ([latex]xy^2[/latex]).
Combine these by the rules of addition.
[latex]\begin{align*}\frac{15x^2y^3+{\color{red}{30xy^2}}-xy+10x^4y}{5xy}\end{align*}[/latex]
Step 2: Now that the numerator is simplified, divide each of its terms by the denominator.
[latex]\begin{align*}\frac{15x^2y^3}{5xy}+\frac{30xy^2}{5xy}-\frac{xy}{5xy}\frac{10x^4y}{5xy}\end{align*}[/latex]
Step 3: Resolve the divisions by dividing both numerical and literal coefficients.
[latex]\begin{align*}&\frac{15x\cancel{{}^2}y^{\cancel3^2}}{5\cancel{xy}}+\frac{30\cancel{x}y^{\cancel2}}{5\cancel{xy}}-\frac{\cancel{xy}}{5\cancel{xy}}\frac{10x^{\cancel4^3}y}{5\cancel{xy}}\\[1ex]&=3xy^2+6y-\frac15+2x^3\end{align*}[/latex]
Step 4: Simplify and combine any like terms.
[latex]3xy^2+6y-{\color{blue}{0.2}}+2x^3[/latex]
Step 5: There are no like terms, so this is the final solution.
Step 6: Write as a statement.
The simplified algebraic expression is [latex]3xy^2+6y-0.2+2x^3[/latex].
Substitution
The ultimate goal of algebra is to represent a relationship between various variables. Although it is beneficial to simplify these relationships where possible and shorten the algebraic expressions, in the end you want to calculate a solution. Substitution involves replacing the literal coefficients of an algebraic expression with known numerical values. Once the substitution has taken place, you solve the expression for a final value.
HOW TO
Perform algebraic substitution
Step 1: Identify the value of your variables.
Assume the algebraic equation is [latex]PV=\frac{\text{FV}}{1+rt}[/latex]. You need to calculate the value of [latex]PV[/latex]. It is known that:
[latex]\begin{eqnarray*}FV&=&\$5,443.82\\r&=&0.12\\t&=&\frac{270}{365}\end{eqnarray*}[/latex]
Step 2: Take the known values and insert them into the equation where their respective variables are located, resulting in:
[latex]PV=\frac{\$5,443.82}{1+(0.12)\left({\displaystyle\frac{270}{365}}\right)}[/latex].
Step 3: Resolve the equation to solve for the variable.
Calculate.
[latex]\begin{eqnarray*}PV&=&\frac{\$5,443.82}{1.088767}\\PV&=&\$5,000.00\end{eqnarray*}[/latex]
Things To Watch Out For
It is common in algebra to represent a variable with more than just one letter. As you can see from the example above, [latex]FV[/latex] is a variable, and it represents future value. This should not be interpreted to be two variables, [latex]F[/latex] and [latex]V[/latex]. Similarly, [latex]PMT[/latex] represents annuity payment. When you learn new formulas and variables, take careful note of how a variable is represented.
As well, some literal coefficients have subscripts. For example, you could see [latex]d_1[/latex] and [latex]d_2[/latex] in the same formula. What sometimes happens is that there is more than one value for the same variable. As you will learn in Chapter 4 about merchandising, when you buy an item you may receive more than one discount rate (what [latex]d[/latex] stands for). Therefore, the first discount gets a subscript of [latex]1[/latex], or [latex]d_1[/latex], and the second discount gets a subscript of [latex]2[/latex], or [latex]d_2[/latex]. This allows you to distinguish between the two values in the equation and substitute the correct value in the correct place.
 Paths To Success
Paths To Success
If you are unsure whether you have simplified an expression appropriately, remember that you can make up your own values for any literal coefficient and substitute those values into both the original and the simplified expressions. If you have obeyed all the rules and simplified appropriately, both expressions will produce the same answer.
For example, assume you simplified [latex]2x + 5x[/latex] into [latex]7x[/latex], but you are not sure if you are right. You decide to let [latex]x = 2[/latex]. Substituting into [latex]2x + 5x[/latex], you get [latex]2(2) + 5(2) = 14[/latex]. Substituting into your simplified expression you get [latex]7(2) = 14[/latex]. Since both expressions produced the same answer, you have direct confirmation that you have simplified correctly.
Example 2.5.7
Substitute and solve the following equation:
[latex]N=L\times(1-d_1)\times(1-d_2)\;\times\;(1-d_3)[/latex].
Where:
[latex]\begin{align*}L&=\$1,999.99\\[2ex]d_1&=35\%\\[2ex]d_2&=15\%\\[2ex]d_3&=5\%\end{align*}[/latex].
Solution
Step 1: Substitute known values into the equation.
[latex]N=\$1,999.99\times(1-0.35)\times(1-0.15)\;\times\;(1-0.05)[/latex]
Step 2: Solve for [latex]N[/latex].
[latex]\begin{eqnarray*}N&=&\$1,999.99\times0.65\times0.85\times0.95\\N&=&\$1,049.74\end{eqnarray*}[/latex]
Step 3: Write as a statement.
The value of [latex]N[/latex] is [latex]\$1,049.74[/latex].
Section 2.5 Exercises
Mechanics
For questions 1–4, simplify the algebraic expressions.
- [latex]2a−3a+4+6a−3[/latex]
- [latex]5b(4b+2)[/latex]
- [latex]\begin{align*}\frac{6x^3+12x^2+13.5x}{3x}\end{align*}[/latex]
- [latex](1+i)^3\times (1+i)^{14}[/latex]
- Evaluate the power [latex]8^{\frac{2}{3}}[/latex]
- Substitute the known variables and solve for the unknown variable:
[latex]I=Prt[/latex] where [latex]P=\$2,500[/latex], [latex]r=0.06[/latex], and [latex]t=\frac{135}{365}[/latex]
Solutions
- [latex]5a+1[/latex]
- [latex]20b^2+10b[/latex]
- [latex]2x^2+4x+4.5[/latex]
- [latex](1+i)^{17}[/latex]
- [latex]4[/latex]
- [latex]I=\$55.48[/latex]
Applications
For questions 7-11, simplify the algebraic expressions.
- [latex](6r^2+10−6r+4r^2−3)−(−12r−5r^2+2+3r)[/latex]
- [latex]\begin{align*}\left[\frac{5x^9+3x^9}{2x}\right]^5\end{align*}[/latex]
- [latex]\begin{align*}\frac{t}{2}+0.75t-t^3+\frac{5t^4}{t}-\frac{2\left(t+t^3\right)}{4}\end{align*}[/latex]
- [latex]\begin{align*}\frac{14\left(1+i\right)+21\left(1+i\right)^4-35\left(1+i\right)^7}{7\left(1+i\right)}\end{align*}[/latex]
- [latex]\begin{align*}\frac{R}{1+0.08\times\frac{183}{365}}+3R\left(1+0.08\times\frac{52}{365}\right)\end{align*}[/latex]
- Evaluate the power: [latex]\begin{align*}\left[\left(\frac{2}{5}\right)^2\right]^2\end{align*}[/latex]
For 13 and 14 substitute the known variables and solve for the unknown variable.
- [latex]\begin{align*}\text{PV}=\frac{\text{FV}}{\left(1+i\right)^\textrm{N}}\end{align*}[/latex] where [latex]\text{FV}=\$3,417.24[/latex], [latex]i=0.05[/latex], and [latex]\text{N}=6[/latex]
- [latex]\begin{align*}\text{PMT}=\frac{FV}{\left[\frac{\left(1+i\right)^{\text{N}}-1}{i}\right]}\end{align*}[/latex] where [latex]\text{FV}=\$10,000[/latex], [latex]\text{N}=17[/latex], and [latex]i=0.10[/latex]
Solutions
- [latex]15r^2+3r+5[/latex]
- [latex]1,024x^{40}[/latex]
- [latex]0.75t+3.5t^3[/latex]
- [latex]2+3(1+i)^3−5(1+i)^6[/latex]
- [latex]3.995628\text{R}[/latex]
- [latex]0.0256[/latex]
- [latex]\text{PV}=\$2,550[/latex]
- [latex]\text{PMT}=\$246.64[/latex]
Challenge, Critical Thinking, & Other Applications
For questions 15-17, simplify the algebraic expressions.
- [latex]\begin{align*}\left[\frac{10a^2b^3c^4}{5b^3c^4}\right]^2+6\left(a^8\right)^{\frac{1}{2}}-\left(3a^2+6\right)\left(3a^2-3\right)\end{align*}[/latex]
- [latex]\begin{align*}\frac{-\left(5x+4y+3\right)\left(2x-5y\right)-\left(10x-2y\right)\left(2y+3\right)}{5}\end{align*}[/latex]
- [latex]\begin{align*}\frac{\left(-3z\right)^3\left(3z^2\right)^2}{\left(2z^3\right)^{-4}}\end{align*}[/latex]
- Substitute the known variables and solve for the unknown variable.
[latex]\begin{align*}\text{FV}_\textrm{ORD}=\text{PMT}\left(1+\%C\right)^{\text{N}-1}\left[\frac{\left[\frac{\left(1+i\right)^{\frac{\text{CY}}{\text{PY}}}}{\left(1+\%C\right)}\right]^{\text{N}}-1}{\frac{\left(1+i\right)^{\frac{\text{CY}}{\text{PY}}}}{\left(1+\%C\right)}-1}\right]\end{align*}[/latex]
where
[latex]\text{PMT}=\$500\text{,}\;\;\;i=0.05\text{,}\;\;\;\%C= 0.02\text{,}\;\;\;\text{CY}=2\text{,}\;\;\;\text{PY}=4\text{,}\;\;\;\text{and}\;\text{N}=20[/latex]
For questions 19-20, evaluate the expression.
- [latex]\begin{align*}\$50,000\times\left(1+\frac{0.10}{12}\right)^{-27}\end{align*}[/latex]
- [latex]\begin{align*}\$995\left[\frac{1-\left(1+0.02\right)^{13}\left(1+\frac{0.09}{4}\right)^{-13}}{\frac{0.09}{4}-0.02}\right]\end{align*}[/latex]
Solutions
- [latex]a^4−9a^2+18[/latex]
- [latex]−2x^2−0.6xy+4.8y^2−7.2x+4.2y[/latex]
- [latex]−3,888z^{19}[/latex]
- [latex]\$15,223.10[/latex]
- [latex]\$39,963.05[/latex]
- [latex]\$12,466.44[/latex]
Attribution
“2.4: Algebraic Expressions” from Business Math: A Step-by-Step Handbook (2021B) by J. Olivier and Lyryx Learning Inc. through a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License unless otherwise noted.

