3.1: Percentages
Formula & Symbol Hub
For this section you will need the following:
Symbols Used
- [latex]\times 100=[/latex] percentage conversion factor
- [latex]\text{Base}=[/latex] the whole quantity
- [latex]\text{dec}=[/latex] decimal number to be converted to percentage
- [latex]\text{Portion}=[/latex] a part of the whole quantity
- [latex]\text{Rate}=[/latex] the relationship between the [latex]\text{Portion}[/latex] and the [latex]\text{Base}[/latex]
Formulas Used
-
Formula 3.1a – Percentage
[latex]\%=\text{dec}\times 100[/latex]
-
Formula 3.1b – Rate, Portion, Base
[latex]\begin{align*}\text{Rate}=\frac{\text{Portion}}{\text{Base}}\end{align*}[/latex]
Introduction
Your class just wrote its first math quiz. You got [latex]13[/latex] out of [latex]19[/latex] questions correct, or [latex]\frac{13}{19}[/latex].
In speaking with your friends Sandhu and Illija, who are in other classes, you find out that they also wrote math quizzes; however, theirs were different. Sandhu scored [latex]16[/latex] out of [latex]23[/latex], or [latex]\frac{16}{23}[/latex] while Illija got 11 out of 16, or [latex]\frac{11}{16}[/latex].
Who achieved the highest grade? Who had the lowest? The answers are not readily apparent, because fractions are difficult to compare.
Now express your grades in percentages rather than fractions. You scored [latex]68\%[/latex], Sandhu scored [latex]70\%[/latex], and Illija scored [latex]69\%[/latex]. Notice you can easily answer the questions now. The advantage of percentages is that they facilitate comparison and comprehension.
Converting Decimals to Percentages
A percentage is a part of a whole expressed in hundredths. In other words, it is a value out of [latex]100[/latex]. For example, [latex]93\%[/latex] means [latex]93[/latex] out of [latex]100[/latex], or [latex]\frac{93}{100}[/latex].
[latex]\boxed{3.1\text{a}}[/latex] Percentage
[latex]\color{red}{\%}\;{\color{black}{\text{is Percentage:}}}[/latex] This is the decimal expressed as a percentage. It must always be written with the percent ([latex]\%[/latex]) symbol immediately following the number.
[latex]\color{green}{\times100}{\color{black}{\text{ is Conversion Factor:}}}[/latex] A percentage is always expressed in hundredths.
[latex]{\color{blue}{\text{dec}}}{\color{black}{\text{ is Decimal Number:}}}[/latex] This is the decimal number needing to be converted into a percentage.
HOW TO
Covert a Decimal to a Percentage
Assume you want to convert the decimal number [latex]0.0875[/latex] into a percentage. This number represents the [latex]\text{dec}[/latex] variable in the formula. Substitute into Formula 3.1a:
[latex]\begin{eqnarray*}\%&=&\text{dec}\times100\\\%&=&0.0875\times100\\\%&=&8.75\%\end{eqnarray*}[/latex]
 Key Takeaways
Key Takeaways
You can also solve this formula for the decimal number. To convert any percentage back into its decimal form, you need to perform a mathematical opposite. Since a percentage is a result of multiplying by [latex]100[/latex], the mathematical opposite is achieved by dividing by [latex]100[/latex]. Therefore, to convert [latex]81\%[/latex] back into decimal form:
[latex]\begin{align*}\frac{81\%}{100}=0.81\end{align*}[/latex]
Things To Watch Out For
Your Texas Instruments BAII Plus calculator has a [latex]\%[/latex] key that can be used to convert any percentage number into its decimal format. For example, if you press [latex]81[/latex] and then [latex]\%[/latex], your calculator displays [latex]0.81[/latex].
While this function works well when dealing with a single percentage, it causes problems when your math problem involves multiple percentages. For example, try keying [latex]4\%+3\%=[/latex] into the calculator using the [latex]\%[/latex] key. This should be the same as [latex]0.04+0.03=0.07[/latex]. Notice, however, that your calculator has [latex]0.0412[/latex] on the display.
Why is this? As a business calculator, you BAII Plus is programmed to take portions of a whole. When you key [latex]3\%[/latex] into the calculator, it takes [latex]3\%[/latex] of the first number keyed in, which was [latex]4\%[/latex]. As a formula, the calculator sees [latex]4\%+(3\%\times 4\%)[/latex]. This works out to [latex]0.04+0.0012=0.0412[/latex].
To prevent this from happening, your best course of action is not to use the [latex]\%[/latex] key on your calculator. It is best to key all percentages as decimal numbers whenever possible, thus eliminating any chance that the [latex]\%[/latex] key takes a portion of your whole. Throughout this textbook, all percentages are converted to decimals before calculations take place.
 Paths To Success
Paths To Success
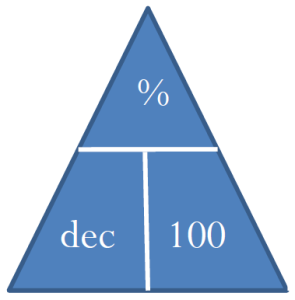
When working with percentages, you can use some tricks for remembering the formula and moving the decimal point.
Remembering the Formula
When an equation involves only multiplication of all terms on one side with an isolated solution on the other side, use a mnemonic called the triangle technique. In this technique, draw a triangle with a horizontal line through its middle. Above the line goes the solution, and below the line, separated by vertical lines, goes each of the terms involved in the multiplication. The figure to the right shows how Formula 3.1a[latex]\%=\text{dec}\times 100[/latex] would be drawn using the triangle technique.
To use this triangle, identify the unknown variable, which you then calculate from the other variables in the triangle:
-
- Anything on the same line gets multiplied together. If solving for [latex]\%[/latex], then the other variables are on the same line and multiplied as [latex]\text{dec}\times 100[/latex].
-
- Any pair of items with one above the other is treated like a fraction and divided. If solving for [latex]\text{dec}[/latex], then the other variables are above/below each other and are divided as [latex]\frac{\%}{100}[/latex].
Moving the Decimal
Another easy way to work with percentages is to remember that multiplying or dividing by [latex]100[/latex] moves the decimal over two places.
- If you are multiplying by [latex]100[/latex], the decimal position moves two positions to the right.

- If you are dividing by [latex]100[/latex], the decimal position moves two positions to the left.

Example 3.1.1
Convert (a) and (b) into percentages. Convert (c) back into decimal format.
- [latex]\begin{align*}\frac{3}{8}\end{align*}[/latex]
- [latex]1.3187[/latex]
- [latex]12.399\%[/latex]
Solution
Step 1: What are we looking for?
For questions (a) and (b), you need to convert these into percentage format. For question (c), you need to convert it back to decimal format.
Step 2: What do we already know?
- This is a fraction to be converted into a decimal, or dec.
- This is dec.
- This is %.
Step 3: Make substitutions using the information known above.
a. Convert the fraction into a decimal to have dec.
[latex]\begin{align*}\text{dec}&=\frac{3}{8}\\[1ex]\text{dec}&=0.375\end{align*}[/latex]
Then apply Formula 3.1a to get the percentage:
[latex]\begin{align*}\%&=\text{dec}\times 100\\\%&=0.375\times 100\\\%&=37.5\%\end{align*}[/latex]
b. As this term is already in decimal format, apply Formula 3.1a to get the percentage.
[latex]\begin{align*}\%&=\text{dec}\times 100\\\%&=1.3187\times 100\\\%&=131.87\%\end{align*}[/latex]
c. This term is already in percentage format. Using the triangle technique, calculate the decimal number through
[latex]\begin{align*}\text{dec}&=\frac{\%}{100}\\[1ex]\text{dec}&=\frac{12.399\%}{100}\\[1ex]\text{dec}&=0.12399\end{align*}[/latex]
Step 4: Provide the information in a worded statement.
In percentage format, the first two numbers are [latex]37.5\%[/latex] and [latex]131.87\%[/latex]. In decimal format, the last number is [latex]0.12399[/latex].
Rate, Portion, Base
In your personal life and career, you will often need to either calculate or compare various quantities involving fractions. For example, if your income is [latex]\$3,000[/latex] per month and you can’t spend more than [latex]30\%[/latex] on housing, what is your maximum housing dollar amount? Or perhaps your manager tells you that this year’s sales of [latex]\$1,487,003[/latex] are [latex]102\%[/latex] of last year’s sales. What were your sales last year?
[latex]\boxed{3.1\text{b}}[/latex] Rate, Portion, Base:
[latex]\color{blue}{\text{Portion}}\color{black}{\text{ is The Part Of The Quantity:}}[/latex] The portion represents the part of the whole. Compare it against the base to assess the rate.
[latex]\color{red}{\text{Rate}}\color{black}{\text{ is The Relationship:}}[/latex] The rate is the decimal form expressing the relationship between the portion and the base. Convert it to a percentage if needed by applying Formula 3.1a[latex]\%=\text{dec}\times 100[/latex]. This variable can take on any value, whether positive or negative.
[latex]\color{green}{\text{Base}}\color{black}{\text{ is The Entire Quantity:}}[/latex] The base is the entire amount or quantity that is of concern. It represents a whole, standard, or benchmark that you assess the portion against.
HOW TO
Calculate Percentage of a Part to the Whole
Assume that your company has set a budget of [latex]\$1,000,000[/latex]. This is the entire amount of the budget and represents your base. Your department gets [latex]\$430,000[/latex] of the budget—this is your department’s part of the whole and represents the portion. You want to know the relationship between your budget and the company’s budget. In other words, you are looking for the rate.
Apply Formula 3.1b:
Your budget is [latex]0.43[/latex], or [latex]43\%[/latex], of the company’s budget.
Key Takeaways
There are three parts to this formula. Mistakes commonly occur through incorrect assignment of a quantity to its associated variable. The table below provides some tips and clue words to help you make the correct assignment.
| Variable | Key Words | Example |
|---|---|---|
| Base | of | If your department can spend 43% of the company’s total budget of $1,000,000, what is your maximum departmental spending? |
| Portion | is, are | If your department can spend 43% of the company’s total budget of $1,000,000, what is your maximum departmental spending? |
| Rate | %, percent, rate | If your department can spend 43% of the company’s total budget of $1,000,000, what is your maximum departmental spending? |
Things To Watch Out For
In resolving the rate, you must express all numbers in the same units—you cannot have apples and oranges in the same sequence of calculations. In the above example, both the company’s budget and the departmental budget are in the units of dollars. Alternatively, you would not be able to calculate the rate if you had a base expressed in kilometres and a portion expressed in metres. Before you perform the rate calculation, express both in kilometres or both in metres.
 Paths To Success
Paths To Success
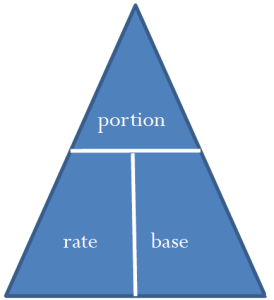
Formula 3.1b[latex]\begin{align*}\text{Rate}=\frac{\text{Portion}}{\text{Base}}\end{align*}[/latex] is another formula you can use the triangle technique for. You do not need to memorize multiple versions of the formula for each of the variables. The triangle appears to the right.
Be very careful when performing operations involving rates, particularly in summing or averaging rates.
Summing Rates
Summing rates requires each rate to be a part of the same whole or base. If Bob has [latex]5\%[/latex] of the kilometres travelled and Sheila has [latex]6\%[/latex] of the oranges, these are not part of the same whole and cannot be added. If you did, what does the [latex]11\%[/latex] represent? The result has no interpretation. However, if there are [latex]100[/latex] oranges of which Bob has [latex]5\%[/latex] and Sheila has [latex]6\%[/latex], the rates can be added and you can say that in total they have [latex]11\%[/latex] of the oranges.
Averaging Rates
Simple averaging of rates requires each rate to be a measure of the same variable with the same base. If [latex]36\%[/latex] of your customers are female and [latex]54\%[/latex] have high income, the average of [latex]45\%[/latex] is meaningless since each rate measures a different variable. Recall that earlier in this chapter you achieved [latex]68\%[/latex] on your test and Sandhu scored [latex]70\%[/latex]. However, your test involved [latex]19[/latex] questions and Sandhu’s involved [latex]23[/latex] questions. These rates also cannot be simply averaged to [latex]69\%[/latex] on the reasoning that [latex]\frac{(68\%+70\%)}{ 2}=69\%[/latex], since the bases are not the same. When two variables measure the same characteristic but have different bases (such as the math quizzes), you must use a weighted-average technique, which is discussed in Section 2.4.
When can you average rates? Hypothetically, assume Sandhu achieved his [latex]70\%[/latex] by writing the same test with [latex]19[/latex] questions. Since both rates measure the same variable and have the same base, the simple average of [latex]69\%[/latex] is now calculable.
Try It
Consider the following situations and select the best answer without performing any calculations.
1) If the rate is [latex]0.25\%[/latex], in comparison to the base the portion is:
- just a little bit smaller than the base.
- a lot smaller than the base.
- just a little bit bigger than the base.
- a lot bigger than the base.
Solution
b. ([latex]0.25\%[/latex] is [latex]0.0025[/latex], resulting in a very small portion)
Try It
Consider the following situations and select the best answer without performing any calculations.
2) If the portion is [latex]\$44,931[/latex] and the base is [latex]\$30,000[/latex], the rate is:
- smaller than [latex]100\%[/latex].
- equal to [latex]100\%[/latex].
- larger than [latex]100\%[/latex] but less than [latex]200\%[/latex].
- larger than [latex]200\%[/latex].
Solution
c. (the portion is larger than the base, but not twice as large)
Try It
Consider the following situations and select the best answer without performing any calculations.
3) If the rate is [latex]75\%[/latex] and the portion is [latex]\$50,000[/latex], the base is:
- smaller than [latex]\$50,000[/latex].
- larger than [latex]\$50,000[/latex].
- the same as the portion and equal to [latex]\$50,000[/latex].
Solution
b. (the portion represents [latex]75\%[/latex] of the base, meaning the base must be larger)
Example 3.1.2
Solve for the unknown in the following three scenarios.
- If your total income is [latex]\$3,000[/latex] per month and you can’t spend more than [latex]30\%[/latex] on housing, what is the maximum amount of your total income that can be spent on housing?
- Your manager tells you that [latex]2014[/latex] sales are [latex]102\%[/latex] of [latex]2013[/latex] sales. The sales for [latex]2014[/latex] are [latex]\$1,487,003[/latex]. What were the sales in [latex]2013[/latex]?
- In Calgary, total commercial real estate sales in the first quarter of [latex]2008[/latex] were [latex]\$1.28\;\text{billion}[/latex]. The industrial, commercial, and institutional (ICI) land sector in Calgary had sales of [latex]\$409.6\;\text{million}[/latex]. What percentage of commercial real estate sales is accounted for by the ICI land sector?
Solution
Step 1: What are we looking for?
- You are looking for the maximum amount of your income that can be spent on housing.
- You need to figure out the sales for [latex]2013[/latex].
- You must determine the percentage of commercial real estate sales accounted for by the ICI land sector in Calgary.
Step 2: What do we already know?
- Look for key words in the question: “what is the maximum amount” and “of your total income.” The total income is the base, and the maximum amount is the portion.
[latex]\begin{align*}\text{Base}&=\$3,000\\\text{Rate}&=30\%\\\text{Portion}&=\text{maximum amount}\end{align*}[/latex]
- Look for key words in the question: “sales for 2014 are $1,487,003″ and “of 2013 sales.” The 2014 sales is the portion, and the 2013 sales is the base.
[latex]\begin{align*}\text{Portion}&=\$1,487,003\\\text{Rate}&=102\%\\\text{Base}&=2013\text{ sales}\end{align*}[/latex]
- Look for key words in the question: “of commercial real estate sales” and “are accounted for by the ICI land sector.” The commercial real estate sales are the base, and the ICI land sector sales are the portion.
[latex]\begin{align*}\text{Base}&=\$1.28\text{ billion}\\\text{Portion}&=\$409.6\text{ million}\\\text{Rate}&=\text{percentage}\end{align*}[/latex]
Step 3: Make substitutions using the information known above.
- Apply Formula 3.1b, but rearrange using the triangle technique to have:
[latex]\begin{align*}\text{Portion}&=\text{Rate}\times\text{Base}\\\text{Portion}&=30\%\times \$3,000\\\text{Portion}&=0.3\times \$3,000\\\text{Portion}&=\$900\end{align*}[/latex]
- Apply Formula 3.1b, but rearrange using the triangle technique to have:
[latex]\begin{align*}\text{Base}&=\frac{\text{Portion}}{\text{Rate}}\\[1ex]\text{Base}&=\frac{\$1,487,003}{102\%}\\[1ex]\text{Base}&=\frac{\$1,487,003}{1.02}\\[1ex]\text{Base}&=\$1,457,846.08\end{align*}[/latex]
- Apply Formula 3.1b:
[latex]\begin{align*}\text{Rate}&=\frac{\text{Portion}}{\text{Base}}\\[1ex]\text{Rate}&=\frac{\$409.6\text{ million}}{\$1.28\text{ billion}}\\[1ex]\text{Rate}&=\frac{\$409,600,000}{\$1,280,000,000}\\[1ex]\text{Rate}&=0.32\\\text{Rate}&=32\%\end{align*}[/latex]
Step 4: Provide the information in a worded statement.
- The maximum you can spend on housing is [latex]\$900[/latex] per month.
- [latex]2013[/latex] sales were [latex]\$1,457,846.08[/latex].
- The ICI land sector accounted for [latex]32\%[/latex] of commercial real estate sales in Calgary for the first quarter of [latex]2008[/latex].
Section 3.1 Exercises
Mechanics
- Convert the following decimals into percentages.
- [latex]0.4638[/latex]
- [latex]3.1579[/latex]
- [latex]0.000138[/latex]
- [latex]0.015[/latex]
- Convert the following fractions into percentages.
- [latex]\begin{align*}\frac{3}{8}\end{align*}[/latex]
- [latex]\begin{align*}\frac{17}{32}\end{align*}[/latex]
- [latex]\begin{align*}\frac{42}{12}\end{align*}[/latex]
- [latex]\begin{align*}2\frac{4}{5}\end{align*}[/latex]
- Convert the following fractions into percentages. Round to four decimals or express in repeating decimal format as needed.
- [latex]\begin{align*}\frac{46}{12}\end{align*}[/latex]
- [latex]\begin{align*}\frac{2}{9}\end{align*}[/latex]
- [latex]\begin{align*}\frac{3}{11}\end{align*}[/latex]
- [latex]\begin{align*}\frac{48}{93}\end{align*}[/latex]
- Convert the following percentages into decimal form.
- [latex]15.3\%[/latex]
- [latex]0.03\%[/latex]
- [latex]153.987\%[/latex]
- d. [latex]14.0005\%[/latex]
- What percentage of [latex]\$40,000[/latex] is [latex]\$27,000[/latex]?
- What is [latex]\frac{1}{2}\%[/latex] of [latex]\$500,000[/latex]?
- [latex]\$0.15[/latex] is [latex]4,900\%[/latex] of what number?
Solutions
1a. [latex]46.38\%[/latex]
1b. [latex]315.79\%[/latex]
1c. [latex]0.0138\%[/latex]
1d. [latex]1.5\%[/latex]
2a. [latex]37.5\%[/latex]
2b. [latex]53.125\%[/latex]
2c. [latex]350\%[/latex]
2d. [latex]280\%[/latex]
3a. [latex]383.\overline{3}\%[/latex]
3b. [latex]22.\overline{2}\%[/latex]
3c. [latex]27. \overline{27}\%[/latex]
3d. [latex]51.6129\%[/latex]
4a. [latex]0.153[/latex]
4b. [latex]0.0003[/latex]
4c. [latex]1.53987[/latex]
4d. [latex]0.140005[/latex]
5. [latex]67.5\%[/latex]
6. [latex]\$2,500[/latex]
7. [latex]\$0.003061[/latex]
Applications
- In February 2009, [latex]14,676[/latex] mortgages were in arrears in Canada, which represented [latex]0.38\%[/latex] of all mortgages. How many total mortgages were in the Canadian market at that time?
- In 2009, medical experts predicted that one out of two Manitobans would contract some form of the H1N1 virus. If the population of Manitoba in 2009 was [latex]1,217,200[/latex], how many Manitobans were predicted to become ill?
- In August 2004, Google Inc. offered its stocks to the public at [latex]\$85[/latex] per share. In October 2007, the share price had climbed to [latex]\$700.04[/latex]. Express the 2007 share price as a percentage of the 2004 price.
- During Michael Jordan’s NBA career (1984–2003), he averaged a free throw completion percentage of [latex]83.5\%[/latex] in regular season play. If Jordan threw [latex]8,772[/latex] free throws in his career, how many completed free throws did he make?
- If total advertising expenditures on television advertising declined [latex]4.1\%[/latex] to [latex]\$141.7[/latex] billion in the current year, how much was spent on television advertising in the previous year? Round your answer to one decimal.
- If the new minimum wage of [latex]\$8.75[/latex] per hour is [latex]102.9412\%[/latex] of the old minimum wage, what was the old minimum wage?
- A machine can produce [latex]2,500[/latex] products per hour. If [latex]37[/latex] of those products were defective, what is the defect rate per hour for the machine?
Solutions
- [latex]3,862,105[/latex]
- [latex]\$608,600[/latex]
- [latex]823.5765\%[/latex]
- [latex]7,325[/latex]
- [latex]\$147.8\;\text{billion}[/latex]
- [latex]\$8.50[/latex]
- [latex]1.48\%[/latex]
Challenge, Critical Thinking, & Other Applications
- In 2011, Manitoba progressive income tax rates were [latex]10.8\%[/latex] on the first[latex]\$31,000[/latex], [latex]12.75\%[/latex] on the next [latex]\$36,000[/latex], and [latex]17.4\%[/latex] on any additional income. If your gross taxable earnings for the year were [latex]\$85,000[/latex], what percentage of your earnings did you pay in taxes?
- In 2011, the maximum amount that you could have contributed to your RRSP (Registered Retirement Savings Plan) was the lesser of [latex]\$22,450[/latex] or [latex]18\%[/latex] of your earned income from the previous year. How much income do you need to claim a [latex]\$22,450[/latex] contribution in 2011?
- 17. Maria, a sales representative for a large consumer goods company, is paid [latex]3\%[/latex] of the total profits earned by her company. Her company averages [latex]10\%[/latex] profit on sales. If Maria’s total income for the year was [latex]\$60,000[/latex], what total sales did her company realize?
- A house was purchased six years ago for [latex]\$214,000[/latex]. Today it lists at a price that is [latex]159.8131\%[/latex] of the original purchase price. In dollars, how much has the price of the house increased over the six years?
- An investor buys [latex]1,000[/latex] shares of WestJet Airlines at [latex]\$10.30[/latex] per share. A few months later, the investor sells the shares when their value hits [latex]120\%[/latex] of the original share price. What is the price of a WestJet share when the investor sells these shares? How much money did the investor make?
- A Honda Insight has fuel economy of [latex]3.2[/latex] litres consumed per [latex]100[/latex] kilometres driven. It has a fuel tank capacity of [latex]40[/latex] litres. A Toyota Prius is rated at [latex]4.2[/latex] L per [latex]100[/latex] km driven. It has a fuel tank capacity of [latex]45[/latex] L. What percentage is the total distance drivable (rounded to the nearest kilometre before calculating) of a Honda Insight compared to that of a Toyota Prius?
Solutions
- [latex]13.0235\%[/latex]
- [latex]\$124,722.22[/latex]
- [latex]\$20,000,000[/latex]
- [latex]\$128,000.03[/latex]
- [latex]\text{Share Price}=\$12.36[/latex]; [latex]\text{Money made}=\$2,060[/latex]
- [latex]116.\overline{6}\%[/latex]
THE FOLLOWING LATEX CODE IS FOR FORMULA TOOLTIP ACCESSIBILITY. NEITHER THE CODE NOR THIS MESSAGE WILL DISPLAY IN BROWSER.[latex]\%=\text{dec}\times 100[/latex][latex]\begin{align*}\text{Rate}=\frac{\text{Portion}}{\text{Base}}\end{align*}[/latex]
Attribution
“2.3 Percentages” from Business Math: A Step-by-Step Handbook (2021B) by J. Olivier and Lyryx Learning Inc. through a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License unless otherwise noted.


