4.2: Invoicing: Terms of Payment and Cash Discounts
Formula & Symbols Hub
For this section you will need the following:
Symbol Used
- [latex]d[/latex] = Discount rate or Cash discount rate
- [latex]L[/latex] = List price or Invoice amount
- [latex]N[/latex] = Net price or Net payment amount
Formulas Used
-
Formula 4.2a – Single Discount Rearranged
[latex]\begin{eqnarray*}L=\frac{N}{(1-d)}\end{eqnarray*}[/latex]
-
Formula 4.2b – Single Discount
[latex]\begin{eqnarray*}N=L\times (1-d)\end{eqnarray*}[/latex]
Introduction
What a way to start your Monday morning! With dread you face a great stack of envelopes in your in-basket. The first envelope contains an invoice from your major supplier indicating an outstanding balance of [latex]\$3,600[/latex] with terms of [latex]2/10[/latex], [latex]1/20[/latex], net [latex]30[/latex]. In the second envelope, an office supplies bill totals [latex]\$500[/latex] with terms of [latex]3/15[/latex], net [latex]45[/latex] EOM. The third envelope holds yet another invoice from your transportation company indicating an outstanding balance of [latex]\$21,000[/latex] with terms of [latex]2/15[/latex], [latex]1/25[/latex], net [latex]60[/latex] ROG. It also indicates that you have an overdue balance of [latex]\$4,000[/latex] subject to a [latex]3\%[/latex] monthly penalty. Before opening any more envelopes that probably contain still more bills, you pour yourself another cup of coffee and settle down to figuring out how much you need to pay and when.
In the world of business, most purchases are not paid for in cash. Instead, businesses tend to work through an invoicing system in which they send out bills to their clients on a regular basis. In accounting, this means that the purchase is placed into accounts receivables until such time as a cheque arrives and the purchase is converted to cash. Invoices provide detailed transaction information, listing the amount owed and also indicating the terms on which payment is expected. Companies may offer what are known as cash discounts as incentives for early invoice payment. The rationale for these discounts is simple—a sale is not a sale until you have the cash in hand. The longer an invoice remains in accounts receivable, the less likely that it will be paid. Thus, it might turn into bad debt, which the creditor cannot collect at all.
Invoicing is less common in consumer purchases because of the sheer volume of transactions involved and the higher risk of nonpayment. Imagine purchasing items at Walmart and receiving an invoice to pay your bill next month instead of paying cash. It is hard to fathom the number of invoices Walmart would have to distribute monthly. How much would it cost to collect those debts? How many of those invoices would go unpaid? That is why consumer purchases typically do not involve invoicing.
Invoicing does commonly occur at a consumer level on credit card transactions along with many services where the business may not be able to assess the exact amount of the bill at the time of the transaction or until the service is delivered. Two examples illustrate this point:
- Think of your MasterCard bill. You are able to make purchases, say, from March 9 to April 8. Then on April 9 the company sends out a statement saying you have until April 29 to pay your bill. If you do not, interest and late payment penalties are involved.
- You have a dental visit for a regular cleaning. Before charging you, the dentist’s office needs to determine how much your insurance will cover. It may not find out the answer for a day or two, so it sends you an invoice at a later date once it hears from the insurance company. The invoice terms indicate that payment is due upon receipt and you will incur late penalties if payment is not forthcoming.
This section explores the most common aspects of invoicing, including terms of payments and cash discounts. You will learn to calculate the amount required to pay invoices and how to reduce the outstanding balance of an invoice if a partial payment is received. Additionally, the calculation of late payments and penalties is introduced.
Invoice Terms and Invoice Dating
You must know how to read a business invoice. The figure on the next page (Kerry Mitchell) provides a sample invoice and highlights the following areas:
- Invoicing Company: The invoice must identify who is sending and issuing the invoice.
- Invoice Date: The date on which the invoice was printed, along with the invoice tracking number (in this case, the order date and shipping date are equivalent to the invoice date). When an invoice is paid, the cheque must reference the invoice number so that the invoicing company can identify which invoice to credit the payment to.
- Transaction Details: The details of the transaction might include number of units, unit prices, and any discounts for which the item is eligible.
- Invoice Total: The total amount owing is indicated, including any taxes or additional charges.
- Terms of Payment: The terms of payment include any cash discounts and due dates. The date of commencement (as discussed below) is determined from this part of the invoice.
- Late Penalty: A penalty, if any, for late payments is indicated on the invoice. Whether or not a company enforces these late penalties is up to the invoice-issuing organization.
Three Dates of Commencement
All invoice terms are affected by what is known as the date of commencement, which is the first day from which all due dates stated on the invoice will stem. The date of commencement is determined in one of three ways as illustrated below.
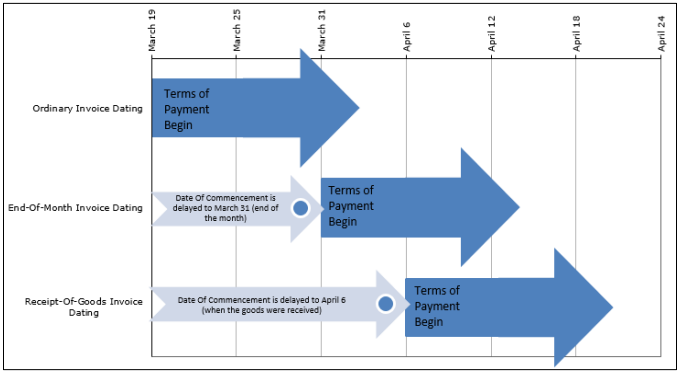
-
Ordinary Invoice Dating:
In ordinary invoice dating, or just invoice dating for short, the date of commencement is the same date as the invoice date. Therefore, if the invoice is printed on March 19, then all terms of payment commence on March 19. This is the default manner in which most companies issue their invoices, so if an invoice does not specify any other date of commencement you can safely assume it is using ordinary dating.
-
End-of-Month Invoice Dating:
End-of-month invoice dating applies when the terms of payment include the wording “end-of-month” or the abbreviation “EOM” appears after the terms of payment. In end-of-month dating, the date of commencement is the last day of the same month as indicated by the invoice date. Therefore, if the invoice is printed on March 19, then all terms of payment commence on the last day of March, or March 31. Many companies use this method of dating to simplify and standardize all of their due dates, in that if the date of commencement is the same for all invoices, then any terms of payment will also share the same dates.
-
Receipt-Of-Goods Invoice Dating:
Receipt-of-goods invoice dating applies when the terms of payment include the wording “receipt-of-goods” or the abbreviation “ROG” appears after the terms of payment. In receipt-of-goods dating, the date of commencement is the day on which the customer physically receives the goods. Therefore, if the invoice is printed on March 19 but the goods are not physically received until April 6, then all terms of payment commence on April 6. Companies with long shipping times involved in product distribution or long lead times in production commonly use this method of dating.
Terms of Payment
The most common format for the terms of paying an invoice is shown below and illustrated by an example.
[latex]\color{blue}{3}\color{black}{\;\text{is Cash Discount:}}[/latex] A cash discount is the percentage of the balance owing on an invoice that can be deducted for payment received either in full or in part during the discount period (see below). In this case, [latex]3\%[/latex] is deducted from the total invoice amount.
[latex]\color{red}{10}\color{black}{\;\text{is Discount Period:}}[/latex] The discount period is the number of days from the date of commencement in which the customer is eligible to take advantage of the cash discount. For this example, there is a period of 10 days during which a payment received in full or any portion thereof is eligible for the [latex]3\%[/latex] cash discount.
[latex]\color{green}{\text{net}\;30}\color{black}{\;\text{is Credit Period:}}[/latex] The credit period is the number of interest-free days from the date of commencement that the customer has to pay the invoice in full before the creditor applies any penalties to the invoice.
—
The figure below plots the invoice term of “[latex]3/10[/latex], net [latex]30[/latex]” along a time diagram to illustrate the terms of payment. This term is combined with various dates of commencement using the examples from the “Date of Commencement” section.
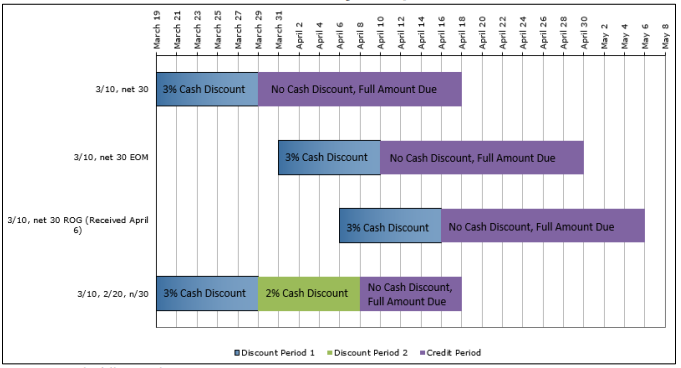
Note the following observations:
- In all four scenarios, the total length of all bars is the same, since the credit period is 30 days.
- Although all four invoices have the same invoice date of March 19, the date of commencement is modified in the ROG and EOM scenarios, which shift the discount and credit periods into the future. In these cases, any payment before the end of the discount period qualifies for the discount.
- For example, in the EOM scenario a company could pay its bill early on March 27 and qualify for the [latex]3\%[/latex] cash discount.
You may see invoice terms displayed in several other common formats:
-
- [latex]3/10[/latex], [latex]n/30[/latex]: In this case, the word “net” has been abbreviated to “[latex]n/[/latex]“. This is illustrated in the fourth scenario in the figure.
- [latex]3/10[/latex], [latex]2/20[/latex], [latex]n/30[/latex]. In this case, multiple cash discounts are being offered, meaning [latex]3\%[/latex] within 10 days from the date of commencement and [latex]2\%[/latex] from the 11th to the 20th day from the date of commencement. This is also illustrated in the fourth scenario of the figure.
- [latex]n/30[/latex]. In this case, no cash discount is offered and only the credit period is identified.
Rules for Invoice Terms
Some common business practices are implemented across most industries. Note that you must always check with the invoicing organization to ensure it is applying these practices.
- No Net Figure: If no net figure is stated in the terms of payment, you should assume that the credit period is 20 days after the last discount period. If there are no discount periods, then the credit period is 20 days from the date of commencement.
For example, “[latex]3/10[/latex], [latex]2/15[/latex]” means that the credit period ends 20 days after the second discount period of 15 days. Hence, the credit period is 35 days after the date of commencement.
- No Cash Discount: Not every invoice receives a cash discount. If no terms indicate a cash discount, then the invoicing company seeks full payment only.
For example, “[latex]n/30[/latex]” means that no cash discount applies and the credit period ends 30 days from the date of commencement.
- Nonbusiness Days: Most businesses operate Monday through Friday and are closed on weekends and holidays. As such, any date falling on a nonworking day is moved to the next business day.
For example, if an invoice is ordinary dated December 21 and lists a cash discount of [latex]2/10[/latex], the end of the discount period falls on January 1. Since this is New Year’s Day, the discount period extends to January 2. In this textbook, you should apply this practice to any of the five known statutory holidays as discussed previously. (New Year’s Day, Good Friday or Easter Monday in Quebec only, Canada Day, Labor Day, and Christmas Day).
Three Types of Payments
When businesses pay invoices, three situations can occur:
- Full Payment: A full payment means that the company wants to pay its invoice in full and reduce its balance owing to zero dollars. This is the most common practice.
- Partial Payment: A partial payment means that the company wants to lower its balance owing but will not reduce that balance to zero. A company will generally employ this method when it wants to either lower its accounts payable or demonstrate good faith in paying its invoices. Partial payment may also occur if the company wants to take advantage of a cash discount but lacks the funds to clear the invoice in its entirety.
- Late Payment: A late payment occurs when the company pays its invoice either in full or partially after the credit period has elapsed. Late payments occur for a variety of reasons, but the most common are either insufficient funds to pay the invoice or a simple administrative oversight.
The rest of this section shows you how to handle each of these types of payments mathematically, and it also explores the implications of cash discounts.
Try It
1) In each of the following cases, determine which term of payment results in the longest credit period extending from the invoice date.
- [latex]2/10[/latex], [latex]n/30[/latex] or [latex]3/15[/latex]
- [latex]3/15[/latex], [latex]n/45[/latex] or [latex]2/10[/latex], [latex]1/20[/latex]
- [latex]2/10[/latex], [latex]n/60[/latex] or [latex]3/10[/latex], [latex]n/30[/latex] EOM on an invoice dated January 7
- [latex]3/15[/latex], [latex]n/45[/latex] or [latex]2/10[/latex], [latex]n/35[/latex] ROG, or [latex]2/20[/latex] EOM on an invoice dated September 22 and goods received on September 29
Solution
- [latex]30[/latex] days or [latex]35[/latex] days
- [latex]45[/latex] days or [latex]40[/latex] days
- [latex]60[/latex] days or [latex]54[/latex] days ([latex]24[/latex] days left in January plus [latex]30[/latex] more)
- [latex]45[/latex] days or [latex]42[/latex] days ([latex]7[/latex] days until received plus [latex]35[/latex]) or [latex]48[/latex] days ([latex]8[/latex] left in month plus [latex]40[/latex] more)
Full Payments
In the opening scenario in this section, the first invoice on your desk was for [latex]\$3,600[/latex] with terms of [latex]2/10[/latex], [latex]1/20[/latex], net [latex]30[/latex]. Suppose that invoice was dated March 19. If you wanted to take advantage of the [latex]2\%[/latex] cash discount, when is the last day that payment could be received, and in what amount would you need to write the cheque? In this section, we will look at how to clear an invoice in its entirety.
[latex]\boxed{4.2\text{a}}[/latex] Single Discount
The good news is that a cash discount is just another type of discount similar to what you encountered in Section 4.1, and you do the calculations using the exact same formula. Apply Formula 4.1a on single discounts, which is reprinted below.
[latex]\color{red}{N}\color{black}{\;\text{is the Net Price:}}[/latex] The net price is the price of the product after the discount is removed from the list price. It is a dollar amount representing what price remains after you have applied the discount.
[latex]\color{green}{L}\color{black}{\;\text{is List Price:}}[/latex] The list price is the normal or regular dollar price of the product before any discounts. It is the Manufacturer’s Suggested Retail Price (MSRP – a price for a product that has been published or advertised in some way), or any dollar amount before you remove the discount.
[latex]\color{blue}{d}\color{black}{\;\text{is the Discount Rate:}}[/latex] The discount rate represents the percentage (in decimal format) of the list price that is deducted.
HOW TO
Work with payments and invoices
Step 1: Look for and identify key information such as the invoice date, date of commencement modifiers such as EOM or ROG, terms of payment, late penalty, and the invoice amount.
Step 2: Draw a timeline similar to the figure on the next page. On this timeline, chronologically arrange from left to right the invoice date and amount, the date of commencement, the end of any discount (if any) or credit periods, cash discounts (if any) that are being offered, and penalties (if any).
Step 3: Determine when payments are being made and in what amount. Locate them on the timeline.
Step 4: Apply the correct calculations for the payment, depending on whether the payment is a full payment, partial payment, or late payment.
Let’s continue with the example of the first invoice on your desk. You mail in a cheque to be received by March 29. What amount is the cheque?
Step 1: The invoice amount is [latex]L = $3,600[/latex], invoice date is March 19, and terms of payment are [latex]2/10[/latex], [latex]1/20[/latex], net [latex]30[/latex].
Step 2: The figure on the next page displays the invoice timeline.
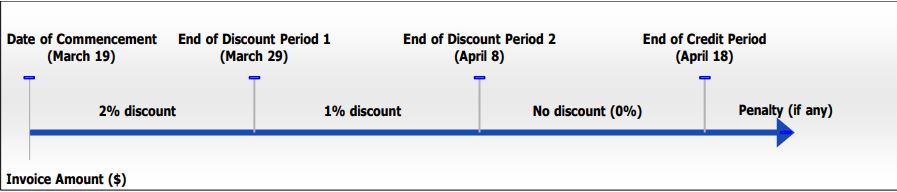
Step 3: Note on the timeline that a payment on March 29 is the last day of the [latex]2\%[/latex] discount period.
Step 4: According to Formula 4.2a[latex]N=L\times\left(1-d\right)[/latex], the amount to pay is:
[latex]\begin{eqnarray*}N&=&\$3,600\times(1-0.02)\\N&=&\$3,600\times0.098\\N&=&\$3,528\end{eqnarray*}[/latex]
A cheque for [latex]\$3,528[/latex] pays your invoice in full. By taking advantage of the cash discount, you reduce your payment by [latex]\$72[/latex].
Things To Watch Out For
If there is one area of invoicing that causes the most confusion, it is assigning information to the net price and invoice amount variables. These are commonly assigned backwards. Remember these rules so that you always get the correct answer:
- The invoice amount or any reference to the balance owing on an invoice is always a list price.
List Price = Invoice Amount
- The payment of an invoice, whether in full, partial, or late, is always a net price.
Net Price = Payment Amount
 Paths To Success
Paths To Success
Who cares about [latex]1\%[/latex] or [latex]2\%[/latex] discounts when paying bills? While these percentages may not sound like a lot, remember that these discounts occur over a very short time frame. For example, assume you just received an invoice for [latex]\$102.04[/latex] with terms of [latex]2/10[/latex], [latex]n/30[/latex]. When taking advantage of the [latex]2\%[/latex] cash discount, you must pay the bill 20 days early, resulting in a [latex]\$100[/latex] payment. That is a [latex]\$2.04[/latex] savings over the course of 20 days. To understand the significance of that discount, imagine that you had [latex]\$100[/latex] sitting in a savings account at your bank. Your savings account must have a balance of [latex]\$102.04[/latex] twenty days later. This requires your savings account to earn an annual interest rate of [latex]44.56\%[/latex]! Therefore, a 20-day [latex]2\%[/latex] discount is the same thing as earning interest at [latex]44.56\%[/latex]. Outrageously good!
Try It
2) In each of the following cases, determine the cash discount or penalty for which the payment qualifies.
| Invoice Date | Terms of Payment | Payment Received on | |
| a. | April 14 | [latex]2/10[/latex], [latex]n/30[/latex] | April 24 |
| b. | July 7 | [latex]3/10[/latex], [latex]2/20[/latex], [latex]n/30[/latex] EOM, [latex]1\%[/latex] per month penalty | August 12 |
| c. | November 12 (goods received November 28) | [latex]2/20[/latex] ROG, [latex]2\%[/latex] per month penalty | December 29 |
| d. | February 27 (non–leap year) | [latex]4/10[/latex], [latex]2/15[/latex], [latex]1/25[/latex] EOM | March 25 |
Solution
- [latex]2\%[/latex] discount
- [latex]2\%[/latex] discount
- No discount ([latex]0\%[/latex]) or penalty
- [latex]1\%[/latex] discount
Example 4.2.1
You receive an invoice for [latex]\$35,545.50[/latex] dated August 14. The terms of payment are listed as [latex]3/10[/latex], [latex]2/20[/latex], net [latex]45[/latex] EOM. The accounting department is considering paying this debt on one of three days. Determine the full payment required if payment is received by the invoicing company on each of the following dates:
a. September 3
b. September 19
c. September 30
Solution
Step 1: Write the known values.
The invoice amount, terms of payment, and any payments are known:
[latex]\begin{eqnarray*}L&=&\$35,545.50\\\text{Invoice Date}&=&\;\text{August 14}\\\text{Terms of Payment}\;&=&\;3/10,\;2/20,\;\text{net}\;45\;\text{EOM}\\\text{Three payment date options are}\;&=&\;\text{Sept. 3, Sept. 19 and Sept. 30}\end{eqnarray*}[/latex]
Step 2: Look at the figure illustrated to see the timeline for the invoice and identification of payments.
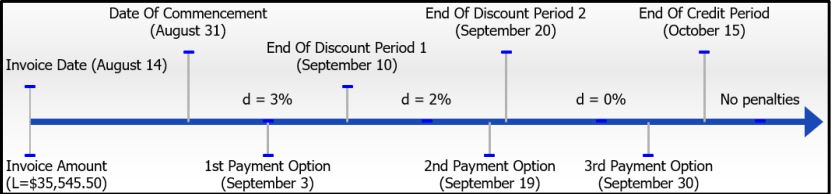
Step 3: Calculate the payment required by applying Formula 4.2a[latex]N=L\times\left(1-d\right)[/latex]. As noted from the timeline:
a. The first payment option qualifies for [latex]d = 3\%[/latex]
b. The second payment option qualifies for [latex]d = 2\%[/latex]
c. The third payment option qualifies for [latex]d = 0\%[/latex] (no cash discount)
Step 4: Substitute values into Formula 4.2a[latex]N=L\times\left(1-d\right)[/latex] and solve.
a. [latex]\begin{eqnarray*}N&=&\$35,545.50\times(1-0.03)\\N&=&\$35,545.50\times0.97\\N&=&\$34,479.14\end{eqnarray*}[/latex]
b. [latex]\begin{eqnarray*}N&=&\$35,545.50\times(1-0.02)\\N&=&\$35,545.50\times0.98\\N&=&\$34,834.59\end{eqnarray*}[/latex]
c. [latex]\begin{eqnarray*}N&=&\$35,545.50\times(1-0)\\N&=&\$35,545.50\times1\\N&=&\$35,545.50\;\text{*No discount, so N=L}\end{eqnarray*}[/latex]
Step 5: Write as a statement.
If the invoicing company receives payment on September 3, a [latex]3\%[/latex] discount is allowed and [latex]\$34,479.14[/latex] clears the invoice. If the payment is received on September 19, a [latex]2\%[/latex] discount is allowed and [latex]\$34,834.59[/latex] pays it off. Finally, if the payment arrives on September 30, there is no discount so the full invoice amount of [latex]\$35,545.50[/latex] is due.
Partial Payments
In the section opener, your third invoice is for [latex]\$21,000[/latex] with terms of [latex]2/15[/latex], [latex]1/25[/latex], net [latex]60[/latex] ROG. After you paid the [latex]\$3,528[/latex] to clear the first invoice, you realize that your company has insufficient funds to take full advantage of the [latex]2\%[/latex] cash discount being offered by the transportation company. Not wanting to lose out entirely, you decide to submit a partial payment of [latex]\$10,000[/latex] before the first discount period elapses. What is the balance remaining on the invoice?
Unless you pay attention to invoicing concepts, it is easy to get confused. Perhaps you think that [latex]\$10,000[/latex] should be removed from the [latex]\$21,000[/latex] invoice total, thereby leaving a balance owing of [latex]\$11,000[/latex]. Or maybe you think the payment should receive the discount of [latex]2\%[/latex], which would be [latex]\$200[/latex]. Are you credited with [latex]\$9,800[/latex] off of your balance? Or maybe [latex]\$10,200[/latex] off of your balance? In all of these scenarios, you would be committing a serious mistake and miscalculating your balance owing. Let’s look at the correct way of handling this payment.
[latex]\boxed{4.2\text{b}}[/latex] Single Discount Rearranged
Recall that invoice amounts are gross amounts (amounts before discounts), or [latex]G[/latex], and that payment amounts are net amounts (amounts after discounts), or [latex]N[/latex]. Also recall that an algebraic equation requires all terms to be expressed in the same unit.
In the case of invoice payments, you can think of the balance owing as being in the unit of “pre-discount” and any payment being in the unit of “post-discount.” Therefore, a payment cannot be directly deducted from the invoice balance since it is in the wrong unit. You must convert the payment from a “post-discount” amount into a “pre-discount” amount using a rearranged version of Formula 4.2a[latex]N=L\times\left(1-d\right)[/latex]. You can then deduct it from the invoice total to calculate any balance remaining.
[latex]\color{red}{L}\color{black}{\;\text{is Invoice Amount:}}[/latex] This is the amount deducted from the invoice balance as a result of the payment. It is what the payment is worth once the cash discount
has been factored into the calculation.
[latex]\color{blue}{N}\color{black}{\;\text{is Net Payment Amount:}}[/latex] This is the actual payment amount made that must be converted into its value toward the invoice total. Since the payment represents an amount after the discount has been removed, you need to find out what it is worth before the cash discount was removed.
[latex]\color{green}{d}\color{black}{\;\text{is Cash Discount Rate:}}[/latex] Any payment received within any discount period, whether in full or partial, is eligible for the specified cash discount indicated in the terms of payment.
HOW TO
Work with Partial Payments
Follow the same invoice payment steps even when working with partial payments. Commonly, once you calculate the gross amount of the payment in Step 4 you will also have to calculate the new invoice balance by deducting the gross payment amount.
Let’s continue working with the [latex]\$21,000[/latex] invoice with terms of [latex]2/15[/latex], [latex]1/25[/latex], net [latex]60[/latex] ROG. Assume the invoice is dated March 19 and the goods are received on April 6. If a [latex]\$10,000[/latex] payment is made on April 21, what balance remains on the invoice?
Step 1: The invoice amount is [latex]\$21,000[/latex], the invoice date is March 19, goods are received on April 6, and the terms of payment are [latex]2/15[/latex], [latex]1/25[/latex], net [latex]60[/latex]. A payment of [latex]\$10,000[/latex] is made on April 21.
Step 2: The figure below shows the invoice timeline.

Step 3: The payment of [latex]\$10,000[/latex] on April 21 falls at the end of the first discount period and qualifies for a [latex]2\%[/latex] discount.
Step 4: To credit the invoice, apply Formula 4.2b[latex]\begin{align*}L=\frac{N}{\left(1-d\right)}\end{align*}[/latex]:
[latex]\begin{align*}L&=\frac{\$10,000}{100\%-2\%}\\[1em]L&=\frac{\$10,000}{98\%}\\[1em]L&=\frac{\$10,000}{0.98}\\[1em]L&=\$10,204.08\end{align*}[/latex]
This means that before any cash discounts, the payment is worth [latex]\$10,204.08[/latex] toward the invoice total. The balance remaining is [latex]\$21,000.00 − \$10,204.08 = \$10,795.92[/latex].
 Key Takeaway
Key Takeaway
In the case where a payment falls within a cash discount period, the amount credited toward an invoice total is always larger than the actual payment amount. If the payment does not fall within any discount period, then the amount credited toward an invoice total is equal to the actual payment amount (since there is no cash discount).
To help you understand why a partial payment works in this manner, assume an invoice is received in the amount of $103.09 and the customer pays the invoice in full during a [latex]3\%[/latex] cash discount period. What amount is paid? The answer is [latex]N = \$103.09(100\% − 3\%) = $100[/latex]. Therefore, any payment of [latex]\$100[/latex] made during a [latex]3\%[/latex] cash discount period is always equivalent to a pre-discount invoice credit of [latex]\$103.09[/latex]. If the balance owing is more than [latex]\$103.09[/latex], that does not change the fact that the [latex]\$100[/latex] payment during the discount period is worth [latex]\$103.09[/latex] toward the invoice balance.
Try It
3) In each of the following situations, determine for the partial payment whether you would credit the invoice for an amount that is larger than, equal to, or less than the partial payment amount.
- An invoice dated April 7 with terms [latex]4/20[/latex], [latex]2/20[/latex], [latex]n/60[/latex] EOM. The goods are received on April 9 and a partial payment is made on May 21.
- An invoice dated July 26 with terms [latex]3/30[/latex], [latex]n/45[/latex] ROG. The goods are received on August 2 and a partial payment is made on September 3.
- An invoice dated January 3 with terms [latex]2½/10[/latex], [latex]1/20[/latex]. The goods are received on January 10 and a partial payment is made on January 24.
Solution
- Since the payment falls within a discount period, the credited amount is larger than the payment.
- Since the payment does not fall within a discount period, the credited amount is equal to the payment.
- Since the payment falls within a discount period, the credited amount is larger than the payment.
Example 4.2.2
Heri just received an invoice from his supplier, R&B Foods. The invoice totaling [latex]\$68,435.27[/latex] is dated June 5 with terms of [latex]2½/10[/latex], [latex]1/25[/latex], [latex]n/45[/latex]. Heri sent two partial payments in the amounts of [latex]\$20,000[/latex] and [latex]\$30,000[/latex] that R&B Foods received on June 15 and June 29, respectively. He wants to clear his invoice by making a final payment to be received by R&B Foods on July 18. What is the amount of the final payment?
Solution
Step 1: Write what you know from the question.
[latex]\begin{eqnarray*}L&=&\$68,435.27\\\text{Invoice Date}&=&\text{June 5}\\[1ex]\text{Terms of Payment }&=&\;\frac{2{\displaystyle\frac{\;1}2}}{10},\;\frac1{25,\;{\displaystyle\frac n{45}}}\\[1ex]N_1&=&\$20,000\;\text{on June 15}\\N_2&=&\$30,000\;\text{on June 29}\\N_3&=&\text{? on July 18}\end{eqnarray*}[/latex]
Step 2: Look at the figure illustrated to see the timeline for the invoice and identification of payments.
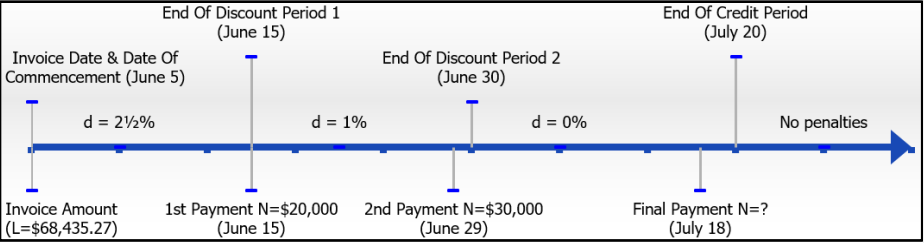
Step 3: The first two payments are partial, reference the timeline.
As noted on the timeline:
a. The first partial payment qualifies for [latex]d = 2½\%[/latex]
b. The second partial payment qualifies for [latex]d = 1\%[/latex]
c. The last payment is a full payment, where [latex]d = 0\%[/latex] (no cash discount)
Step 4: Apply Formula 4.2b[latex]\begin{align*}L=\frac{N}{\left(1-d\right)}\end{align*}[/latex]
a.
[latex]\begin{eqnarray*}L&=&\frac{\$20,000}{(1-0.025)}\\[1ex]L&=&\frac{\$20,000}{0.975}\\[1ex]L&=&\$20,512.82\\[2ex]\text{Balance Owing}&=&\$68,435.27-\$20,512.82\\\text{Balance Owing}&=&\$47,922.45\end{eqnarray*}[/latex]
b.
[latex]\begin{eqnarray*}L&=&\frac{\$30,000}{(1-0.01)}\\[1ex]L&=&\frac{\$30,000}{0.99}\\[1ex]L&=&\$30,303.03\\[2ex]\text{Balance Owing}&=&\$47,922.45\;-\$30,303.03\\\text{Balance Owing}&=&\$17,619.42\end{eqnarray*}[/latex]
c. Since there is no cash discount, [latex]N_3\;=\;L[/latex]. The balance owing is [latex]L = \$17,619.42[/latex].
Therefore, the payment is the same number and [latex]N_3 = \$17,619.42[/latex].
Step 5: Write as a statement.
The first two payments receive a credit of [latex]\$20,512.82[/latex] and [latex]\$30,303.03[/latex] toward the invoice total, respectively. This leaves a balance on the invoice of [latex]\$17,619.42[/latex]. Since the final payment is made during the credit period, but not within any cash discount period, the final payment is the exact amount of the balance owing and equals [latex]\$17,619.42[/latex].
Late Payment Penalties
Among all of the invoices that you were paying in the section opener, you realize upon opening that third envelope that you somehow missed an invoice last month and failed to pay the [latex]\$4,000[/latex] owing, which is now overdue. In looking at the invoice, you notice that it states on the bottom that late payments are subject to a [latex]3\%[/latex] per month penalty. You urgently want to pay this invoice to maintain good relations with your supplier but wonder in what amount you must issue the cheque?
Why Do Late Penalties Exist?
Suppliers are doing their business customers a favor when they use invoicing to seek payment. In essence, suppliers provide the products to the customer but are not paid for those products up front. This means customers are granted a period during which they “borrow” the products for free without any associated interest costs that are usually tied to borrowing. If the invoice is not paid in full by the time the credit period elapses, then the supplier starts treating any remaining balance like a loan and charges interest, which is called a late payment penalty.
The Formula
When a payment arrives after the credit period has expired, you need to adjust the balance of the invoice upward to account for the penalty. Continue to use Formula 4.2a[latex]N=L\times\left(1-d\right)[/latex] on Single Discounts for this calculation. In this unique case, the discount rate represents a penalty. Instead of deducting money from the balance, you add a penalty to the balance. As a result, the late penalty is a negative discount.
For example, if the penalty is [latex]3\%[/latex] then [latex]d = −3\%[/latex].
HOW TO
Work with Late Payments
Follow the same steps to solve the invoice payment once again when working with late payments. As an example, work with the [latex]\$4,000[/latex] overdue invoice that is subject to a [latex]3\%[/latex] per month late penalty. If the invoice is paid within the first month of being overdue, what payment is made?
Step 1: The invoice balance is [latex]L = \$4,000[/latex], and the penalty percent is [latex]d = −0.03[/latex].
Steps 2 & 3: Since the focus is strictly on the late payment calculation, you do not need a timeline for the discount or credit periods. The late payment occurs within the first month past the expiry of the credit period.
Step 4: To determine the new invoice balance, apply Formula 4.2a[latex]N=L\times\left(1-d\right)[/latex] to calculate:
[latex]\begin{eqnarray*}N&=&\;\$4,000\;\times\;(1\;-\;(-0.03))\;\\N&=&\;\$4,000\;\times\;1.03\;\\N&=&\;\$4,120\end{eqnarray*}[/latex]
Therefore, to clear the invoice you must issue a cheque in the amount of [latex]\$4,120[/latex]. This covers the [latex]\$4,000[/latex] owing along with a late penalty of [latex]\$120[/latex].
 Key Takeaways
Key Takeaways
Not all invoices have penalties, nor are they always enforced by the supplier. There are many reasons for this:
- Most businesses pay their invoices in a timely manner, which minimizes the need to institute penalties.
- Waiving a penalty maintains good customer relations and reinforces a positive, cooperative business partnership.
- Strict application of late penalties results in difficult situations. For example, if a payment was dropped in the mail on August 13 from your best customer and it arrives one day after the credit period expires on August 15, do you penalize that customer? Is it worth the hassle or the risk of upsetting the customer?
- The application of late penalties generally involves smaller sums of money that incur many administrative costs. The financial gains from applying penalties may be completely wiped out by the administrative expenses incurred.
- Businesses have other means at their disposal for dealing with delinquent accounts. For example, if a customer regularly pays its invoices in an untimely manner, the supplier may just to decide to withdraw the privilege of invoicing and have the customer always pay up front instead.
In this textbook, all penalties are strictly and rigidly applied. If a payment is late, the invoice balance has the appropriate late penalty applied.
Things To Watch Out For
When a late penalty is involved, you must resist the temptation to adjust the payment by the penalty percentage. The discussion and calculations in this section focus on adjusting the outstanding invoice balance to figure out the payment required. For example, assume there is a [latex]\$500[/latex] outstanding balance subject to a [latex]2\%[/latex] penalty.
- This means that with the penalty, the invoice total is [latex]\$510[/latex], which determines that a payment of [latex]\$510[/latex] is required.
- If the customer makes a [latex]\$200[/latex] partial payment on this late debt, you cannot apply the partial payment procedure, which would give a credit of [latex]\$204.08[/latex] for the payment, resulting in a balance owing of [latex]\$295.92[/latex]. If you make this mistake, you in fact reward the customer for being tardy!
- Nor can you deduct the [latex]2\%[/latex] penalty from the payment and give credit for [latex]\$200(1 – 0.02) = \$196[/latex] (resulting in a balance owing of [latex]\$304[/latex]) because the [latex]2\%[/latex] penalty applies to the whole invoice amount and not just the partial payment.
- Instead, the [latex]\$200[/latex] payment must be deducted directly from the penalty-adjusted balance of [latex]\$510[/latex]. In this case, the customer still owes [latex]\$310[/latex] to clear the invoice.
 Paths To Success
Paths To Success
An alternative method for applying a late penalty is to treat the penalty like a positive percent change (see Section 3.1). In this case, the penalty is how much you want to increase the balance owing. Thus, if an invoice for [latex]\$500[/latex] is subject to a [latex]2\%[/latex] penalty, the [latex]\%C\;=\;2\%[/latex] and [latex]Old = \$500[/latex]. The goal is to look for the new balance ([latex]V_\textrm{f}[/latex]) in Formula 3.2b[latex]\begin{align*}RoC=\left(\left(\frac{V_\textrm{f}}{V_\textrm{i}}\right)^{\frac{1}{n}}\right)\times 100\end{align*}[/latex]: [latex]V_\textrm{f} = \$510[/latex].
Example 4.2.3
You received an invoice dated December 17 in the amount of [latex]\$53,455.55[/latex] with terms of [latex]4/15[/latex], [latex]2/30[/latex], [latex]n/60[/latex] ROG, [latex]2.75\%[/latex] penalty per month for late payments. The merchandise is received on January 24. You sent in a partial payment of [latex]\$40,000[/latex] on January 31 with intention to pay the remaining balance before the credit period expired. However, you forgot about the invoice and realized your mistake on March 30, when you submit payment in full for the invoice. What amount is the final payment? (Note: Assume this is not a leap year).
Solution
Step 1: Write the known information.
[latex]\begin{eqnarray*}L&=&\$53,455.55\\\text{Invoice Date}&=&\text{December 17}\\\text{Goods Recieved}&=&\text{January 24}\\[1ex]\text{Terms of Payment}&=&\;\frac4{15,\;{\displaystyle\frac2{30}}},\;\frac n{60}\;\text{ROG},\;\frac{2.75\%}{\text{month}}\;\text{late payment penalty}\\[1ex]N_1&=&\$40,000\;\text{on January 31}\\N_2&=&\text{? on March 30}\end{eqnarray*}[/latex]
Step 2: Look at the figure illustrated to see the timeline for the invoice and identification of payments.
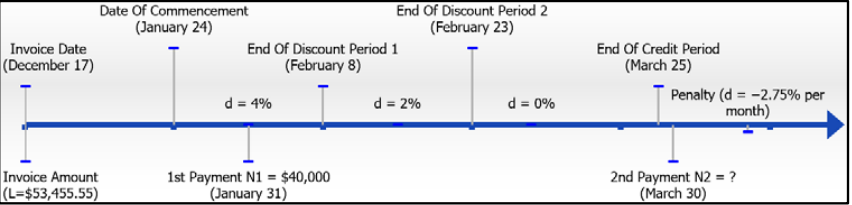
Step 3: Credit the partial payment during the discount period [latex](d = 4\%)[/latex] by applying the rearranged Formula 4.2a[latex]N=L\times\left(1-d\right)[/latex].
[latex]\begin{eqnarray*}(\text{Partial Payment})\;L&=&\frac{\$40,000}{(1-0.04)}\\[1ex]L&=&\frac{\$40,000}{0.96}\\[1ex]L&=&\$41,666.67\end{eqnarray*}[/latex]
Step 4: Deduct the partial payment from the invoice total.
[latex]\begin{eqnarray*}(\text{New Invoice Balance})\;\text{Balancing Owing}&=&\$53,455.55-\$41,666.67\\\text{Balance Owing}&=&\$11,788.88\end{eqnarray*}[/latex]
Step 5: The second payment occurs after the credit period elapses. Therefore the outstanding invoice balance is penalized by [latex]d=−0.0275[/latex] as per the policy. Apply Formula 4.2a[latex]N=L\times\left(1-d\right)[/latex]
This calculates the outstanding balance including the penalty, which equals the final payment.
[latex]\begin{eqnarray*}(\text{Late Payment}):\;N&=&\$11,788.88\times(1-(-0.0275))\\N&=&\$11,788.88\times1.0275\\N&=&\$12,113.07\end{eqnarray*}[/latex]
Step 6: Write as a statement.
The first payment resulted in a [latex]\$41,666.67[/latex] deduction from the invoice. The overdue remaining balance of [latex]\$11,788.88[/latex] has a penalty of [latex]\$324.19[/latex] added to it, resulting in a final clearing payment of [latex]\$12,113.07[/latex].
Section 4.2 Exercises
Round all money to two decimals and percentages to four decimals for each of the following exercises. In all questions, assume that the dates indicated are the dates upon which the payment is received.
Mechanics
For questions 1–3, calculate the full payment required on the payment date that reduces the balance on the invoice to zero. Assume this is not a leap year.
| Invoice Amount | Invoice Date | Invoice Terms | Receipt of Goods Date | Date of Full Payment | |
| 1. | [latex]\$136,294.57[/latex] | January 14 | [latex]2/10[/latex], [latex]n/30[/latex] | January 10 | January 22 |
| 2. | [latex]\$98,482.75[/latex] | September 28 | [latex]3/10[/latex], [latex]2/20[/latex], [latex]1/30[/latex], [latex]n/50[/latex] EOM | October 3 | October 19 |
| 3. | [latex]\$48,190.38[/latex] | February 21 | [latex]4/15[/latex], [latex]3/40[/latex], [latex]n/60[/latex] ROG | February 27 | April 3 |
For questions 4–6, calculate the remaining invoice balance after crediting the invoice for the partial payments indicated.
| Invoice Amount | Invoice Date | Invoice Terms | Receipt of Goods Date | Partial Payments and Dates | |
| 4. | [latex]\$57,775.00[/latex] | June 16 | [latex]3/15[/latex], [latex]1\frac{1}{2}/25[/latex] | June 12 | [latex]\$20,000[/latex] on July 2;
[latex]\$15,000[/latex] on July 10 |
| 5. | [latex]\$1,200,310.75[/latex] | August 25 | [latex]2\frac{1}{2}/10[/latex], [latex]1/20[/latex], [latex]n/30[/latex] ROG | September 2 | [latex]\$500,000[/latex] on September 4;
$250,000 on September 14 |
| 6. | [latex]\$17,481.68[/latex] | December 3 | [latex]4/10[/latex], [latex]1/30[/latex], [latex]n/60[/latex] EOM | December 20 | [latex]\$10,000[/latex] on January 2 |
For questions 7–8, calculate the final payment required on the payment date that reduces the balance of the invoice to zero.
| Invoice Amount | Invoice Date | Invoice Terms | Late Payment Penalty | Receipt of Goods Date | Partial Payments and Dates | Final Payment Date | |
| 7. | [latex]\$23,694.50[/latex] | April 13 | [latex]3/15[/latex], [latex]2/25[/latex], [latex]1/40[/latex], [latex]n/60[/latex] | [latex]1\frac{1}{2}\%[/latex] per month | April 18 | [latex]\$10,000[/latex] on April 30 | June 15 |
| 8. | [latex]\$332,053.85[/latex] | October 4 | [latex]4/10[/latex] EOM | [latex]2\%[/latex] per month | October 30 | [latex]\$100,000[/latex] on November 5 | December 15 |
Solutions
- [latex]\$133, 568.68[/ latex]
- [latex]\$96, 513.10[/ latex]
- [latex]\$46, 744.67[/ latex]
- [latex]\text{ Balance Remaining } = \$21, 928.01[/ latex]
- [latex]\text{ Balance Remaining } = \$434, 964.99[/ latex]
- [latex]\text{ Balance Remaining } = \$7, 065.01[/ latex]
- [latex]\$13, 692.78[/ latex]
- [latex]\$232, 444.92[/ latex]
Applications
- Hudson's Bay received an invoice dated July 13 from Nygard International in the amount of [latex]\$206,731.75[/latex]. The terms are [latex]2/10[/latex], [latex]1/20[/latex], [latex]n/30[/latex]. If Nygard receives full payment on August 1, what amount is paid?
- Time Bomb Traders Inc. in Burnaby just received an invoice dated February 17 (of a leap year) from UrbanEars headphones in the amount of [latex]\$36,448.50[/latex] with terms of [latex]1½/15[/latex], [latex]½/30[/latex], [latex]n/45[/latex] ROG. The items on the invoice are received on March 3. What amount is the full payment if UrbanEars receives it on March 18?
- Family Foods received an invoice dated July 2 from Kraft Canada in the amount of [latex]\$13,002.96[/latex] with terms of [latex]2/15[/latex], [latex]1/30[/latex], [latex]n/45[/latex] EOM and a late penalty of [latex]2\%[/latex] per month. What amount is paid in full if Kraft Canada receives a cheque from Family Foods on August 17?
- An invoice dated November 6 in the amount of [latex]\$38,993.65[/latex] with terms of [latex]2½/10[/latex], [latex]1/15[/latex] ROG, [latex]2\%[/latex] penalty per month is received by Cargill Limited from Agricore United. The wheat shipment is received on December 2. Cargill Limited made a partial payment of [latex]\$15,000[/latex] on December 10. What amount should Cargill pay to clear its invoice on December 13?
- Yamaha Music received two invoices from the same vendor. The first is for [latex]\$1,260[/latex] dated March 9 with terms [latex]3/10[/latex], net [latex]30[/latex]. The second is for [latex]\$2,450[/latex] dated March 12 with terms [latex]2/10[/latex], [latex]1/20[/latex], net [latex]30[/latex]. If a payment of [latex]\$1,000[/latex] is made on March 19, what payment amount on March 31 settles both invoices? (Note: Payments are applied to the earlier invoice first.)
- An invoice is dated July 26 for [latex]\$5,345.50[/latex] with terms of [latex]3¼/10[/latex], net [latex]45[/latex], [latex]2½\%[/latex] per month penalty. If the invoice is paid on September 10, what payment amount is required to pay the entire balance owing?
- Mohawk College received an invoice dated August 20 from Office Depot for office supplies totalling [latex]\$10,235.97[/latex] with terms of [latex]3¾/15[/latex], [latex]1½/30[/latex], [latex]n/45[/latex], EOM, [latex]2¾\%[/latex] per month penalty. The college made three payments of [latex]\$2,000[/latex] dated September 4, September 29, and October 10. What payment on October 25 settles the invoice?
Solutions
- [latex]\$204,664.43[/latex]
- [latex]\$35,901.77[/latex]
- [latex]\$12,872.93[/latex]
- [latex]\$23,372.94[/latex]
- [latex]\$2,654.57[/latex]
- [latex]\$5,479.14[/latex]
- [latex]\$4,241.10[/latex]
Challenge, Critical Thinking, & Other Applications
- An invoice for [latex]\$100,000[/latex] dated February 2 (of a non–leap year) with terms of [latex]4/10[/latex], [latex]3/20[/latex], [latex]2/30[/latex], [latex]1/40[/latex], net [latex]60[/latex], ROG, [latex]1¾\%[/latex] per month penalty. The merchandise is received on February 16. If four equal payments are made on February 20, March 17, April 1, and April 20 resulting in full payment of the invoice, calculate the amount of each payment.
- An accounting department receives the following invoices from the same vendor and makes the indicated payments. The vendor always applies payments to the earliest invoices first and its late payment policy stands at [latex]1½\%[/latex] per month for any outstanding balance.
| Invoice # | Invoice Amount | Invoice Date | Invoice Terms | Receipt of Goods Date |
| 3866 | [latex]\$47,690.11[/latex] | June 18 | [latex]2/10[/latex], EOM | July 3 |
| 2928 | [latex]\$123,691.82[/latex] | June 26 | [latex]2½/15[/latex], [latex]1/25[/latex] | July 6 |
| 4133 | [latex]\$96,004.21[/latex] | June 30 | [latex]2/20[/latex], ROG | July 7 |
| 6767 | [latex]\$16,927.50[/latex] | July 10 | [latex]2/10[/latex], [latex]1/20[/latex] | July 11 |
| Payment Received by Vendor on | Payment Amount |
| July 2 | [latex]\$40,000[/latex] |
| July 11 | [latex]\$75,000[/latex] |
| July 21 | [latex]\$100,000[/latex] |
| July 30 | [latex]\$25,000[/latex] |
Calculate the amount of the final payment on August 17 that reduces the total balance owing to zero.
- John's Home Hardware was invoiced on May 29 for the following non-taxable items with terms of [latex]2/20[/latex], [latex]1/40[/latex], [latex]2\%[/latex] per month penalty.
| Item | Quantity | Unit Price |
| 2"x 4"x 8' framing studs | [latex]13,000[/latex] | [latex]\$0.96[/latex] |
| 4"x 4" x 8' fence posts | [latex]2,400[/latex] | [latex]\$2.87[/latex] |
| 2"x 8"x 16' wood planks | [latex]480[/latex] | [latex]\$8.47[/latex] |
| 1"x 6"x 5' fence boards | [latex]8,000[/latex] | [latex]\$1.22[/latex] |
If a partial payment of [latex]\$20,000[/latex] is made on July 7, what payment amount on August 30 reduces the balance owing to zero? What is the total dollar amount of the late penalty?
- Your company receives a [latex]\$138,175.00[/latex] invoice dated April 12 with terms of [latex]4/10[/latex], [latex]3/20[/latex], [latex]2/30[/latex], [latex]1/40[/latex], [latex]n/60[/latex]. Due to the large amount, the accounting department proposes two different ways to pay this invoice, depending on company income and financing alternatives. These plans are listed in the table below.
| Payment Date | Plan #1 | Plan #2 |
| April 21 | [latex]\$35,000[/latex] | [latex]\$50,000[/latex] |
| May 2 | [latex]\$20,000[/latex] | [latex]\$10,000[/latex] |
| May 10 | [latex]\$25,000[/latex] | [latex]\$50,000[/latex] |
| May 13 | [latex]\$30,000[/latex] | [latex]\$20,000[/latex] |
| June 11 | Balance owing | Balance owing |
-
-
- Which alternative do you recommend?
- If your recommendation is followed, how much money is saved over the other option?
-
| Payment Date | Payment Amount |
| August 14 | [latex]\$67,000.00[/latex] |
| August 28 | [latex]\$83,000.00[/latex] |
| September 18 | [latex]\$15,000.00[/latex] |
| September 30 | [latex]\$83,297.16[/latex] |
Solutions
- [latex]\$24,772.64[/latex]
- [latex]\$40,608.80[/latex]
- [latex]N = \$13,511.24[/latex]; Late penalty amount = [latex]\$519.66[/latex]
- a. Choose Plan #2; b. Savings = [latex]\$724.92[/latex]
- [latex]\$250,214.41[/latex]
THE FOLLOWING LATEX CODE IS FOR FORMULA TOOLTIP ACCESSIBILITY. NEITHER THE CODE NOR THIS MESSAGE WILL DISPLAY IN BROWSER.[latex]\begin{align*}L=\frac{N}{\left(1-d\right)}\end{align*}[/latex][latex]N=L\times(1−d)[/latex][latex]N=L\times\left(1-d\right)[/latex][latex]\begin{align*}RoC=\left(\left(\frac{V_\textrm{f}}{V_\textrm{i}}\right)^{\frac{1}{n}}\right)\times 100\end{align*}[/latex]
Attribution
"7.4: Invoicing: Terms of Payment and Cash Discounts" from Business Math: A Step-by-Step Handbook (2021B) by J. Olivier and Lyryx Learning Inc. through a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License unless otherwise noted.

