6.2: Determining the Future (Maturity) Value
Formula & Symbol Hub
For this section you will need the following:
Symbols Used
- [latex]\text{C/Y}=[/latex] Compounds per year
- [latex]FV=[/latex] Future value or maturity value
- [latex]i=[/latex] Periodic interest rate
- [latex]\text{I/Y}=[/latex] Nominal interest rate per year
- [latex]n=[/latex] Total number of compounding periods
- [latex]PV=[/latex] Present value or principal value
Formulas Used
-
Formula 6.1 - Periodic Interest Rate
[latex]\begin{align*}i=\frac{\text{I/Y}}{\text{C/Y}}\end{align*}[/latex]
-
Formula 6.2a - Number of Compound Periods
[latex]n=\text{C/Y}\times\text{Number of Years}[/latex]
-
Formula 6.2b - Future (Maturity) Value
[latex]FV=PV\times(1+i)^n[/latex]
Determining the Future (Maturity) Value
The simplest future value scenario for compound interest is for all of the variables to remain unchanged throughout the entire transaction. To understand the derivation of the formula, continue with the following scenario. If [latex]\$4,000[/latex] was borrowed two years ago at [latex]12\%[/latex] compounded semi-annually, then a borrower will owe two years of compound interest in addition to the original principal of [latex]\$4,000[/latex]. That means [latex]PV=\$4,000[/latex]. The compounding frequency is semi-annually, or twice per year, which makes the periodic interest rate [latex]i=\frac{\text{I/Y}}{\text{C/Y}}=\frac{12\%}{2}=6\%[/latex]. Therefore, after the first six months, the borrower has [latex]6\%[/latex] interest converted to principal. This a future value, or [latex]FV[/latex], calculated as follows:
Principal after one compounding period (six months) = Principal plus interest:
[latex]\begin{eqnarray}FV &=&PV+{i}(PV)\\FV&=&\$ 4,000+0.06(\$4,000)\\FV&=&\$ 4,000+\$ 240\\FV&=&\$ 4,240\end{eqnarray}[/latex]
Now proceed to the next six months. The future value after two compounding periods (one year) is calculated in the same way.
Note that the equation [latex]FV = PV +i(PV)[/latex] can be factored and rewritten as [latex]FV = PV(1 +i)[/latex].
[latex]\begin{eqnarray*}FV_\textrm{after two compounding periods}&=&PV(1 +i)\\FV_\textrm{after two compounding periods}&=&\$4,240(1 + 0.06)\\FV_\textrm{after two compounding periods}&=&\$4,240(1.06)\\FV_\textrm{after two compounding periods}&=&\$4,494.40\end{eqnarray*}[/latex]
Since the [latex]PV = $4,240[/latex] is the result of the previous calculation where [latex]PV(1 + i) = $4,240[/latex], the following algebraic substitution is possible:
[latex]\begin{eqnarray*}FV_\textrm{after two compounding periods}&=&PV(1 +i )(1 + i)\\FV_\textrm{after two compounding periods}&=&\$4,000(1.06)(1.06)\\FV_\textrm{after two compounding periods}&=&\$4,240(1.06)\\FV_\textrm{after two compounding periods}&=&\$4,494.40\end{eqnarray*}[/latex]
Simplifying algebraically, you get:
[latex]\begin{eqnarray*}FV&=&PV(1 +i)(1 + i)\\FV&=&PV(1 +i)^2\end{eqnarray*}[/latex]
Do you notice a pattern? With one compounding period, the formula has only one [latex](1 + i)[/latex]. With two compounding periods involved, it has two factors of [latex](1 + i)[/latex]. Each successive compounding period multiplies a further [latex](1 + i)[/latex] onto the equation. This makes the exponent on the [latex](1 + i)[/latex] exactly equal to the number of times that interest is converted to principal during the transaction.
The Formula
First, you need to know how many times interest is converted to principal throughout the transaction. You can then calculate the future value. Use Formula 6.2a below to determine the number of compound periods involved in the transaction.
[latex]\boxed{6.2\text{a}}[/latex] Number of Compound Periods
[latex]\color{red}{n}[/latex] is the total number of compounding periods.
[latex]\color{blue}{\text{C/Y}}[/latex] is the number of compounding periods per year.
[latex]\color{green}{\text{Number of Years}}[/latex] is the total number of years.
Once you know [latex]n[/latex], substitute it into Formula 6.2b, which finds the amount of principal and interest together at the end of the transaction, or the future (maturity) value, [latex]FV[/latex].
[latex]\boxed{6.2\text{b}}[/latex] Future (Maturity) Value
[latex]\color{red}{FV}[/latex] is Future or Maturity Value.
[latex]\color{blue}{PV}[/latex] is the Present Value or principal. This is the starting amount upon which compound interest is calculated.
[latex]\color{green}{i}[/latex] is the periodic interest rate from Formula 6.1[latex]\begin{align*}i=\frac{\text{I/Y}}{\text{C/Y}}\end{align*}[/latex].
[latex]\color{purple}{n}[/latex] is the number of compound periods from Formula 6.2a[latex]n=\text{C/Y}\times\text{Number of Years}[/latex].
Key Takeaways
Calculating the Interest Amount ([latex]I[/latex])
In any situation of lump-sum compound interest, you can isolate the interest amount using the formula
[latex]I=FV−PV[/latex]
HOW TO
Calculate the Future Value of a Singe Payment
Follow these steps to calculate the future value of a single payment:
Step 1: Calculate the periodic interest rate using Formula 6.1:
[latex]\begin{align*}i=\frac{\text{I/Y}}{\text{C/Y}}\end{align*}[/latex]
Step 2: Calculate the total number of compound periods ([latex]n[/latex][latex]n[/latex]) using Formula 6.2a:
[latex]n=C/Y \times \text{(Number of years)}[/latex]
Step 3: Calculate the future value using Formula 6.2b:
[latex]FV=PV(1+i)^n[/latex]
Note: You will first need to calculate [latex]i[/latex] and [latex]n[/latex] using Steps 1 and 2.
Your BAII Plus Calculator
We will be using the function keys that are presented in the third row of your calculator, known as the [latex]TVM[/latex] row or (time value of money row). The five buttons located on the third row of the calculator are five of the seven variables required for time value of money calculations. This row’s buttons are different in color from the rest of the buttons on the keypad.

The table below relates each button (variable) to its meaning:
| Variable | Meaning |
|---|---|
| N | Number of compounding periods |
| I/Y | Interest rate per year (nominal interest rate). This is entered in percent form (without the % sign). For example, 5% is entered as 5. |
| PV | Present value or principal |
| PMT | Periodic annuity payment. For lump sum payments set this variable to zero. |
| FV |
Future value or maturity value.
|
| C/Y | Pressing 2ND key then I/Y will open the P/Y worksheet. P/Y stands for periodic payments per year and this will be covered in annuities. We only need to assign a value for C/Y as the calculation does not involve an annuity. We need to set payments per year (P/Y) to the same value as the number of compounding periods per year (C/Y) then press ENTER. When you scroll down (using the down arrow key), you will notice that C/Y will automatically be set to the same value. Pressing 2nd then CPT (Quit button) will close the worksheet. |
Cash Flow Sign Convention
Calculating FV (PV is given)
For investments: When money is invested (paid-out), this amount is considered as a cash-outflow and this amount has to be entered as a negative number for [latex]PV[/latex].
For Loans: When money is received (loaned), this amount is considered as a cash-inflow and this amount has to be entered as a positive number for [latex]PV[/latex].
Calculating PV (FV is given)
For investments: When you receive your matured investment at the end of the term this is considered as a cash-inflow for you and the future value should be entered as a positive amount.
For Loans: When the loan is repaid at the end of the term this is considered as a cash-outflow for you and the future value should be entered as a negative amount.
Key Takeaways
When you compute solutions on the BAII Plus calculator, one of the most common error messages displayed is "Error 5." This error indicates that the cash flow sign convention has been used in a manner that is financially impossible. Some examples of these financial impossibilities include loans with no repayment or investments that never pay out. In these cases, the [latex]PV[/latex] and [latex]FV[/latex] have been incorrectly set to the same cash flow sign.
BAII Plus Memory
Your calculator has permanent memory. Once you enter data into any of the time value buttons it is permanently stored until
-
- You override it by entering another piece of data and pressing the button;
- You clear the memory of the time value buttons by pressing 2nd CLR TVM before proceeding with another question; or
- The reset button on the back of the calculator is pressed.
Example 6.2.1
If you invested [latex]\$5,000[/latex] for [latex]10[/latex] years at [latex]9\%[/latex] compounded quarterly, how much money would you have? What is the interest earned during the term?
Solution
The timeline for the investment is below.

Step 1: Given information:
[latex]PV=5,000[/latex]; [latex]\text{I/Y}=9\%[/latex]; [latex]\text{C/Y}=4[/latex]
Step 2: Calculate the periodic interest rate, [latex]i[/latex].
[latex]\begin{eqnarray*}i&=&\frac{\text{I/Y}}{\text{C/Y}}\\[1ex]i&=&\frac{9\%}{4}\\[1ex]i&=&2.25\%\\i&=&0.0225\end{eqnarray*}[/latex]
Step 3: Calculate the total number of compoundings, [latex]n[/latex].
[latex]\begin{eqnarray*}n&=&\text{C/Y}\times (\text{Number of Years})\\n&=&4 \times 10\\n&=&40\end{eqnarray*}[/latex]
Step 4: Solve for the future value, [latex]FV[/latex].
[latex]\begin{eqnarray*}FV&=&\$5,000(1+0.0225)^{40}\\FV&=&\$12,175.94\end{eqnarray*}[/latex]
Step 5: Find the interest earned.
[latex]\begin{eqnarray*}I&=&FV-PV\\I&=&\$12,175.94-\$5,000\\I&=&\$7,175.94\end{eqnarray*}[/latex]
Calculator instructions:
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 40 | 9 | -5,000 | 0 | ? | 12 | 12 |
Step 6: Write as a statement.
After [latex]10[/latex] years, the principal grows to [latex]\$12,175.94[/latex], which includes your [latex]\$5,000[/latex] principal and [latex]\$7,175.94[/latex] of compound interest.
Future Value Calculations with Variable Changes
What happens if a variable such as the nominal interest rate, compounding frequency, or even the principal changes somewhere in the middle of the transaction? When any variable changes, you must break the timeline into separate time fragments at the point of the change. To arrive at the solution, you need to work from left to right one time segment at a time using Formula 6.2b[latex]FV=PV\times(1+i)^n[/latex].
HOW TO
Calculate Future Value From Lump-Sum Compound Interest
Follow these steps when variables change in calculations of future value based on lump-sum compound interest:
Step 1: Read and understand the problem. Identify the present value. Draw a timeline broken into separate time segments at the point of any change. For each time segment, identify any principal changes, the nominal interest rate, the compounding frequency, and the length of the time segment in years.
Step 2: For each time segment, calculate the periodic interest rate ([latex]i[/latex]) using Formula 6.1[latex]\begin{align*}i=\frac{\text{I/Y}}{\text{C/Y}}\end{align*}[/latex]
Step 3: For each time segment, calculate the total number of compound periods ([latex]n[/latex]) using Formula 6.2a[latex]n=\text{C/Y}\times\text{Number of Years}[/latex] .
Step 4: Starting with the present value in the first time segment (starting on the left), solve for the future value using Formula 6.2b[latex]FV=PV\times(1+i)^n[/latex] .
Step 5: Let the future value calculated in the previous step become the present value for the next step. If the principal changes, adjust the new present value accordingly.
Step 6: Using Formula 6.2b[latex]FV=PV\times(1+i)^n[/latex] calculate the future value of the next time segment.
Step 7: Repeat Steps 5 and 6 until you obtain the final future value from the final time segment.
Key Takeaways
The BAII Plus Calculator:
Transforming the future value from one time segment into the present value of the next time segment does not require re-entering the computed value. Instead, apply the following technique:
- Load the calculator with all known compound interest variables for the first time segment.
- Compute the future value at the end of the segment.
- With the answer still on your display, adjust the principal if needed, change the cash flow sign by pressing the ± key, and then store the unrounded number back into the present value button by pressing [latex]PV[/latex]. Change the [latex]N[/latex], [latex]I/Y[/latex], and [latex]C/Y[/latex] as required for the next segment.
- Return to step 2 for each time segment until you have completed all time segments.
Concept Check
Example 6.2.2
Five years ago Coast Appliances was supposed to upgrade one of its facilities at a quoted cost of [latex]\$48,000[/latex]. The upgrade was not completed, so Coast Appliances delayed the purchase until now. The construction company that provided the quote indicates that prices rose [latex]6\%[/latex] compounded quarterly for the first [latex]1\frac{1}{2}[/latex] years, [latex]7\%[/latex] compounded semi-annually for the following [latex]2\frac{1}{2}[/latex] years, and [latex]7.5\%[/latex] compounded monthly for the final year. If Coast Appliances wants to perform the upgrade today, what amount of money does it need?
Solution
The timeline below shows the original quote from five years ago until today.
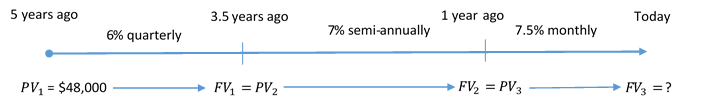
Step 1: First time segment:
[latex]PV_1=\$48,000[/latex]; [latex]\text{I/Y}=6\%[/latex]; [latex]\text{C/Y}=4[/latex]; [latex]\text{Years}=2[/latex]
[latex]\begin{eqnarray*}i&=&\frac{\text{I/Y}}{\text{C/Y}}\\[1ex]i&=&\frac{6\%}{4}\\[1ex]i&=&1.5\%\\\\n&=&\text{C/Y}\times\left(\text{Number of Years}\right)\\n&=&4\times 1.5\\n&=&6\end{eqnarray*}[/latex]
Find [latex]FV_1[/latex]
[latex]\begin{eqnarray}FV_1&=&PV_1(1+i)^n\\FV_1&=&\$48,000(1+0.015)^6\\FV_1&=&\$24,500(1.015)^6\\FV_1&=&\$52,485.27667\end{eqnarray}[/latex]
This becomes [latex]PV_2[/latex] for the next calculation in Step 2.
Step 2: Second line segment:
[latex]PV_2=FV_1=\$52,485.27667[/latex]; [latex]\text{I/Y}=7\%[/latex]; [latex]\text{C/Y}=2[/latex]; [latex]\text{Years}=2.5[/latex]
[latex]\begin{eqnarray*}i&=&\frac{\text{I/Y}}{\text{C/Y}}\\[1ex]i&=&\frac{7\%}2\\[1ex]i&=&3.5\%\\\\n&=&\text{C/Y}\times\left(\text{Number of Years}\right)\\n&=&2\times2.5\\n&=&5\end{eqnarray*}[/latex]
Find [latex]FV_2[/latex]
[latex]\begin{eqnarray}FV_2&=&PV_2(1 + i)^n\\FV_2&=&\$52,485.27667(1+0.035)^5\\FV_2&=&\$62,336.04435\end{eqnarray}[/latex]
This becomes [latex]PV_3[/latex] for the next calculation in Step 3.
Step 3: Third line segment:
[latex]PV_3=FV_2=\$62,336.04435[/latex]; [latex]\text{I/Y}=7.5\%[/latex]; [latex]\text{C/Y}=12[/latex]; [latex]\text{Years}=1[/latex]
[latex]\begin{eqnarray*}i&=&\frac{\text{I/Y}}{\text{C/Y}}\\[1ex]i&=&\frac{7.5\%}{12}\\[1ex]i&=&0.625\%\\\\n&=&\text{C/Y}\times\left(\text{Number of Years}\right)\\n&=&12\times 1\\n&=&12\end{eqnarray*}[/latex]
Find [latex]FV_3[/latex]
[latex]\begin{eqnarray}FV_3&=&PV_3(1 + i)^n\\FV_3&=&\$62,336.04435 (1+0.00325)^{12}\\FV_3&=&\$67,175.35\end{eqnarray}[/latex]
The future value is [latex]\$67,175.35[/latex].
Calculator instruction:
| Step | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| 1 | 6 | 6 | 48,500 | 0 | ? | 4 | 4 |
| 2 | 5 | 7 | 52,485.27667 | 0 | ? | 2 | 2 |
| 3 | 12 | 7.5 | 62,336.04435 | 0 | ? | 12 | 12 |
Step 4: Write as a statement.
Coast Appliances requires [latex]\$67,175.35[/latex] to perform the upgrade today. This consists of [latex]\$48,000[/latex] from the original quote plus [latex]\$19,175.35[/latex] in price increases.
Example 6.2.3
Two years ago Lorelei placed [latex]\$2,000[/latex] into an investment earning [latex]6\%[/latex] compounded monthly. Today she makes a deposit to the investment in the amount of [latex]\$1,500[/latex]. What is the maturity value of her investment three years from now?
Solution
The timeline for the investment is below.

Step 1: First time segment:
[latex]PV_1=\$2,000[/latex]; [latex]\text{I/Y}=6\%[/latex]; [latex]\text{C/Y}=12[/latex]; [latex]\text{Years=2}[/latex]
[latex]\begin{eqnarray*}i&=&\frac{\text{I/Y}}{\text{C/Y}}\\[1ex]i&=&\frac{6\%}{12}\\[1ex]i&=&0.5\%\\\\n&=&\text{C/Y}\times(\text{Number of Years})\\n&=&12\times2\\n&=&24\end{eqnarray*}[/latex]
Find [latex]FV_1[/latex]
[latex]\begin{eqnarray}FV_1&=&PV_1(1+i)^n\\FV_1&=&\$2,000(1+0.005)^24\\FV_1&=&\$2,000(1.005)^24\\FV_1&=&\$2,254.319552\end{eqnarray}[/latex]
[latex]\$2,254.319552+\$1,500=\$3,754.319552[/latex]
This becomes [latex]PV_2[/latex] for the second line segment in Step 2.
Step 2: Second line segment:
[latex]PV_1=FV_1=3,754.319552[/latex]; [latex]\text{I/Y}=6\%[/latex]; [latex]\text{C/Y}=12[/latex]; [latex]\text{Years}= 3[/latex]
[latex]\begin{eqnarray*}i&=&\frac{\text{I/Y}}{\text{C/Y}}\\[1ex]i&=&\frac{6\%}{12}\\[1ex]i&=&0.5\%\\\\n&=&\text{C/Y}\times\text{(Number of Years)}\\n&=&12\times3\\n&=&36\end{eqnarray*}[/latex]
Find [latex]FV_2[/latex]
[latex]\begin{eqnarray}FV_2&=&PV_2(1+i)^n\\FV_2&=&\$3,754.319552(1+0.005)^{36}\\FV_2&=&\$4,492.72\end{eqnarray}[/latex]
The future value is [latex]\$4,492.72[/latex]
Calculator instructions:
| Step | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| 1 | 24 | 6 | -2,000 | 0 | ? | 12 | 12 |
| 2 | 36 | 6 | -3,754.319552 | 0 | ? | 12 | 12 |
Step 3: Write as a statement.
Three years from now Lorelei will have [latex]\$4,492.72[/latex]. This represents [latex]\$3,500[/latex] of principal and [latex]\$992.72[/latex] of compound interest.
Section 6.2 Exercises
In each of the exercises that follow, try them on your own. Full solutions are available should you get stuck.
- Find the future value if [latex]\$53,000[/latex] is invested at [latex]6\%[/latex] compounded monthly for [latex]4[/latex] years and [latex]3[/latex] months.
Solution
Step 1: Given information:
[latex]PV=\$53,000[/latex]; [latex]\text{I/Y}=6\%[/latex]; [latex]\text{C/Y}=12[/latex]; [latex]t=4\frac{3}{12}\;\text{years}[/latex]
Step 2: Find [latex]i[/latex].
[latex]\begin{eqnarray*}i&=&\frac{\text{I/Y}}{\text{C/Y}}\\[1ex]i&=&\frac{6\%}{12}\\i&=&0.5\%\end{eqnarray*}[/latex]
Step 3: Find [latex]n[/latex].
[latex]\begin{eqnarray*}n&=&\text{C/Y}\times\left(\text{Number of Years}\right)\\[1ex]n&=&12\times\left(4\frac3{12}\right)\\[1ex]n&=&4.25\times12\\n&=&51\end{eqnarray*}[/latex]
Step 4: Solve for [latex]FV[/latex].
[latex]\begin{eqnarray*}FV&=&PV\left(1+i\right)^{51}\\FV&=&\$53,000\left(1+0.005\right)^{51}\\FV&=&\$53,000\left(1.005\right)^{51}\\FV&=&\$68,351.02\end{eqnarray*}[/latex]
Step 5: Write as a statement.
The future value is [latex]\$68,351.02[/latex].
Calculator instructions:
[latex]\text{N}=51[/latex]
[latex]\text{I/Y}=6[/latex]
[latex]\text{PV}=-53,000[/latex]
[latex]\text{PMT}=0[/latex]
[latex]\text{P/Y}=12[/latex]
[latex]\text{C/Y}=12[/latex]
[latex]\text{CPT FV}=\$68,351.02[/latex] - Find the future value if [latex]\$24,500[/latex] is invested at [latex]4.1\%[/latex] compounded annually for [latex]4[/latex] years; then [latex]5.15\%[/latex] compounded quarterly for [latex]1[/latex] year, [latex]9[/latex] months; then [latex]5.35\%[/latex] compounded monthly for [latex]1[/latex] year, [latex]3[/latex] months.
Solution
Step 1: Find [latex]FV_1[/latex].
[latex]\begin{eqnarray*}i&=&\frac{\text{I/Y}}{\text{C/Y}}\\[1ex]i&=&\frac{4.1\%}1\\[1ex]i&=&4.1\%\\\\n&=&\text{C/Y}\times\left(\text{Number of Years}\right)\\n&=&1\times4\\n&=&4\\\\FV_1&=&PV_1\left(1+i\right)^n\\FV_1&=&\$24,500\left(1+0.041\right)^4\\FV_1&=&\$28,771.03049\;\text{(This becomes}\;PV\;\text{in Step 2)}\end{eqnarray*}[/latex]
Step 2: Find [latex]FV_2[/latex].
[latex]\begin{eqnarray*}i&=&\frac{\text{I/Y}}{\text{C/Y}}\\[1ex]i&=&\frac{5.15\%}4\\[1ex]i&=&1.2875\%\\\\n&=&\text{C/Y}\times\left(\text{Number of Years}\right)\\[1ex]n&=&4\times\left(1\frac9{12}\right)\\[1ex]n&=&1.75\times4\\n&=&7\\\\FV_2&=&PV_2\left(1+i\right)^n\\FV_2&=&\$28,771.93049\left(1.012875\right)^7\\FV_2&=&\$31,467.33516\;\left(\text{This becomes}\;PV\;\text{in Step 3}\right)\end{eqnarray*}[/latex]
Step 3: Find [latex]FV_3[/latex]
[latex]\begin{eqnarray*}i&=&\frac{\text{I/Y}}{\text{C/Y}}\\[1ex]i&=&\frac{5.35\%}{12}\\[1ex]i&=&0.4458\overline3\\\\n&=&\text{C/Y}\times\left(\text{Number of Years}\right)\\[1ex]n&=&12\times\left(1\frac3{12}\right)\\[1ex]n&=&1.25\times12\\n&=&15\\\\FV_3&=&PV_3\left(1+i\right)^n\\FV_3&=&\$31,467.33516\left(1.004468\overline3\right)^{15}\\FV_3&=&\$33,638.67\end{eqnarray*}[/latex]
Step 4: Write as a statement.
The future value is [latex]\$33,638.67[/latex].
Calculator Instructions:
[latex]\text{N}=4[/latex]
[latex]\text{I/Y}=4.1[/latex]
[latex]PV=-24,500[/latex]
[latex]\text{PMT}=0[/latex]
[latex]\text{P/Y}=1[/latex]
[latex]\text{C/Y}=1[/latex]
[latex]\text{CPT FV}=\$28,771.93049\;(\text{This becomes negative PV in Step 2.})[/latex] - Nirdosh borrowed [latex]\$9,300[/latex] at [latex]6.35\%[/latex] compounded semi-annually [latex]4\frac{1}{4}[/latex] years ago. The interest rate changed to [latex]6.5\%[/latex] compounded quarterly [latex]1\frac{3}{4}[/latex] years ago. What amount of money today is required to pay off this loan?
Solution
Step 1: Find [latex]FV_1[/latex].
[latex]\begin{eqnarray*}i&=&\frac{\text{I/Y}}{\text{C/Y}}\\[1ex]i&=&\frac{6.35\%}2\\[1ex]i&=&2\times2.5\\i&=&3.175\%\\\\n&=&\text{C/Y}\times\left(\text{Number of Years}\right)\\n&=&2\times2.5\\n&=&5\\\\FV_1&=&PV\left(1+i\right)^n\\FV_1&=&\$9,300\left(1.03175\right)^5\\FV_1&=&\$10,873.14892\;\left(\text{This becomes}\;PV\;\text{in Step 2}\right)\end{eqnarray*}[/latex]
Step 2: Find [latex]FV_2[/latex].
[latex]\begin{eqnarray*}i&=&\frac{\text{I/Y}}{\text{C/Y}}\\[1ex]i&=&\frac{6.5\%}4\\i&=&1.625\%\\\\n&=&\text{C/Y}\times\left(\text{Number of Years}\right)\\n&=&4\times1.75\\n&=&7\\\\FV_1&=&PV\left(1+i\right)^n\\FV_1&=&\$10,873.14892\left(1.001625\right)^7\\FV_1&=&\$12,171.92\;\left(\text{Round at this step}\right)\end{eqnarray*}[/latex]
Step 3: Write as a statement.
It is required today [latex]\$12,171.92[/latex] to pay off the loan.
Calculator Instructions for Step 1 and Step 2:
Step 1:
[latex]\text{N}=5[/latex]
[latex]\text{I/Y}=6.35[/latex]
[latex]PV=9,300[/latex]
[latex]\text{PMT}=0[/latex]
[latex]\text{P/Y}=2[/latex]
[latex]\text{C/Y}=2[/latex]
[latex]\text{CPT FV}=\$10,873.14892\;\left(\text{This becomes negative}\;PV\;\text{in Step 2}\right)[/latex]Step 2:
[latex]\text{N}=7[/latex]
[latex]\text{I/Y}=6.5[/latex]
[latex]PV=-10,873.14892[/latex]
[latex]\text{PMT}=0[/latex]
[latex]\text{P/Y}=4[/latex]
[latex]\text{C/Y}=4[/latex]
[latex]\text{CPT FV}=\$12,171.92[/latex]
THE FOLLOWING LATEX CODE IS FOR FORMULA TOOLTIP ACCESSIBILITY. NEITHER THE CODE NOR THIS MESSAGE WILL DISPLAY IN BROWSER.[latex]n=\text{C/Y}\times\text{Number of Years}[/latex][latex]FV=PV\times(1+i)^n[/latex][latex]\begin{align*}i=\frac{\text{I/Y}}{\text{C/Y}}\end{align*}[/latex]
Attribution
"9.2 Determining the Future (Maturity) Value" from Business Math: A Step-by-Step Handbook Abridged by Sanja Krajisnik; Carol Leppinen; and Jelena Loncar-Vines is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

