4.5: Merchandising
Formula & Symbols Hub
In this section you will need the following:
Symbols Used
- [latex]\times 100[/latex] = Percentage multiplier
- [latex]C[/latex] = Cost
- [latex]E[/latex] = Expenses
- [latex]\text{M}\$[/latex] = Markup amount
- [latex]MoC\%[/latex] = Markup on cost percentage
- [latex]\text{MoS}\%[/latex] = Markup on selling price percentage
- [latex]P[/latex] = Profit
- [latex]P_{red}[/latex] = Reduced profit
- [latex]S_{red}[/latex] = Reduced sale price
Formulas Used
-
Formula 4.3a -The Selling Price of a Product
[latex]\text{S}=\text{C}+\text{E}+\text{P}[/latex]
-
Formula 4.3b - Markup Amount
[latex]\text{M}\$=\text{E}+\text{P}[/latex]
-
Formula 4.3d - Markup on Cost Percentage
[latex]\begin{align*}MoC\%=\frac{\text{M}\$}{\text{C}}\times 100\end{align*}[/latex]
-
Formula 4.3e - Markup on Selling Price Percentage
[latex]\begin{align*}\text{MoS}\%=\frac{\text{M}\$}{\text{S}}\times 100\end{align*}[/latex]
-
Formula 4.4b - Markdown Amount
[latex]\$M=S\times d[/latex]
-
Formula 4.4c - Reduced Sale Price
[latex]S_{red}=S-D[/latex]
-
Formula 4.5a - Reduced Profit
[latex]\begin{eqnarray*}P_{red}=S_{red}-C-E\end{eqnarray*}[/latex]
-
Formula 4.5b - Reduced Profit
[latex]\begin{eqnarray*}P_{red}=P-E\end{eqnarray*}[/latex]
Introduction
Running a business requires you to integrate all of the concepts in this chapter. From discounts to markups and markdowns, all the numbers must fit together for you to earn profits in the long run. It is critical to understand how pricing decisions affect the various financial aspects of your business and to stay on top of your numbers.
Merchandising does not involve difficult concepts, but to do a good job of it you need to keep track of many variables and observe how they relate to one another. Merchandising situations in this section will apply all of the previously discussed pricing concepts. Next, the concept of maintained markup helps you understand the combined effect of markup and markdown decisions on list profitability. Finally, you will see that coupons and rebates influence expenses and profitability in several ways beyond the face value of the discounts offered.
The Complete Pricing Picture
Up to this point, you have examined the various components of merchandising as separate topics. Your study of basic product pricing has included the following:
- Taking an MSRP or list price and applying discounts to arrive at a product’s cost
- Marking up a product by adding expenses and profits to the cost to arrive at a regular selling price
- Marking down a product by applying a discount and arriving at a sale price
- Working with various percentages in both markup and markdown situations to either simplify calculations or present a clearer pricing picture
Now is the time to tie all of these merchandising concepts together. Section 4.3 introduced the concept of a markup chart to understand the relationship between various markup components. The figure below extends this figure to include all of the core elements of merchandising.
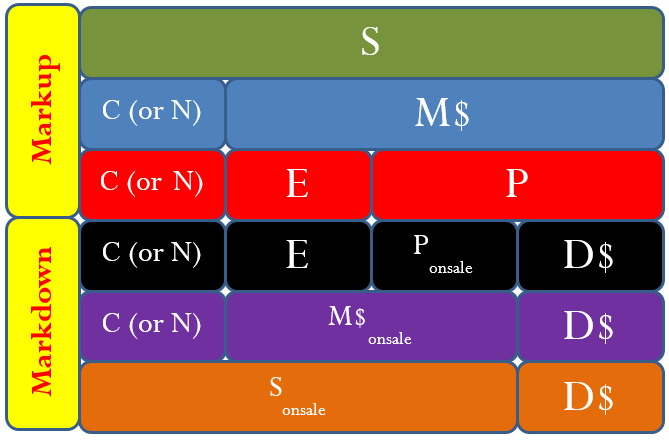
The figure reveals the following characteristics:
- You calculate the cost of a product by applying a discount formula. The net price, [latex]N[/latex], is synonymous with cost, [latex]C[/latex].
- If Markdown ([latex]D[/latex]) [latex]<[/latex] Profit ([latex]P[/latex]) then the reduced profit ([latex]P_{red}[/latex]) will be positive. Also, [latex]S_{red}[/latex] will be greater than [latex]BE[/latex] (breakeven). Therefore, there will be reduced profit at the sale price.
- If Markdown ([latex]D[/latex]) [latex]<[/latex] Profit ([latex]P[/latex]) then the reduced profit ([latex]P_{red}[/latex]) will be [latex]0[/latex]. Also, [latex]S_{red}[/latex] will be equal to [latex]BE[/latex] (breakeven). Therefore, there will be neither profit nor loss at the sale price.
- If Markdown ([latex]D[/latex]) [latex]>[/latex] Profit ([latex]P[/latex]) then the reduced profit ([latex]P_{red}[/latex]) will be negative. Also, [latex]S_{red}[/latex] will be less than [latex]BE[/latex] (breakeven). Therefore, there will be loss at the sale price.
- When you mark a product down, not only is the profit reduced but the markup dollars are also reduced. The following relationships exist when a product is on sale:
[latex]\begin{eqnarray*}{M\$}_{onsale}&=&\;E\; \;P_{onsale}\;\;\;\text{OR}\;\;\;\;\\M\$_{onsale}&=&M\$-D\$\;\;\\P_{onsale}&=&P-D\$\end{eqnarray*}[/latex]
- At break-even (remember, [latex]P[/latex] or [latex]P_{onsale}[/latex] is zero) a sale product has the following relationships:
[latex]\begin{eqnarray*}{M\$}_{onsale}&=&E\;\;\\S_{onsale}&=&C E\;\;\\D\$&=&P\end{eqnarray*}[/latex]
None of these relationships represent new formulas. Instead, these reflect a deeper understanding of the relationships between the markup and markdown formulas.
[latex]\boxed{4.5\text{a}}[/latex] Reduced Profit
So we can conclude that:
[latex]\boxed{4.5\text{b}}[/latex] Reduced Profit
We can also also know that:
The relationship of formulas 4.5a and 4.5b can also be represented using the Table below: a Merchandising Calculation Table.
|
Merchandising Calculation Table |
|||
|
|
Amount | Rate | |
|
|
on [latex]C[/latex] | On [latex]S[/latex] | |
| [latex]P[/latex] |
|
|
|
| [latex]+E[/latex] |
|
|
|
| [latex]M[/latex] |
|
|
|
| [latex]+C[/latex] | |||
| [latex]S[/latex] | |||
| [latex]-D[/latex] | |||
| [latex]S_{red}[/latex] | |||
| ** [latex]{\color{blue}{-C}}[/latex] | |||
| **[latex]{\color{blue}{-E}}[/latex] | |||
| [latex]P_{red}[/latex] | |||
| **[latex]{\color{blue}{-BE}}[/latex] | |||
HOW TO
Solve complete merchandising scenarios
Step 1: It is critically important to correctly identify both the known and unknown merchandising variables that you are asked to calculate.
Step 2: For each of the unknown variables in Step 1, examine Formula 4.1a through Formula 4.5b. Locate which formulas contain the unknown variable. You must solve one of these formulas to arrive at the answer. Based on the information provided, examine these formulas to determine which formula may be solvable. Write out this formula, identifying which components you know and which components remain unknown.
For example, assume that in Step 1 you were asked to solve for the expenses, or [latex]E[/latex]. In looking at the formulas, you find this variable appears only in Formula 4.3a[latex]\text{S}=\text{C}+\text{E}+\text{P}[/latex] and Formula 4.3b[latex]\text{M}\$=\text{E}+\text{P}[/latex], meaning that you must use one of these two formulas to calculate the expenses. Suppose that, in reviewing the known variables from Step 1, you already have the markup amount and the profit. In this case, Formula 4.3b[latex]\text{M}\$=\text{E}+\text{P}[/latex] would be the right formula to calculate expenses with.
Step 3: Note the unknown variables among all the formulas written in Step 2. Are there common unknown variables among these formulas? These common variables are critical variables. Solving for these common unknowns is the key to completing the question. Note that these unknown variables may not directly point to the information you were requested to calculate, and they do not resolve the merchandising scenario in and of themselves. However, without these variables you cannot solve the scenario.
For example, perhaps in Step 1 you were requested to calculate both the markup on cost percent ([latex]MoC\%[/latex]) and the markup on selling price percent ([latex]MoS\%[/latex]). In Step 2, noting that these variables are found only in Formula 4.3d[latex]\begin{align*}MoC\%=\frac{\text{M}\$}{\text{C}}\times 100\end{align*}[/latex] and Formula 4.3e[latex]\begin{align*}\text{MoS}\%=\frac{\text{M}\$}{\text{S}}\times 100\end{align*}[/latex], you wrote them down. Examination of these formulas revealed that you know the cost and selling price variables. However, in both formulas the markup dollars remain unknown.
Therefore, markup dollars is the critical unknown variable. You must solve for markup dollars using Formula 4.3b[latex]\text{M}\$=\text{E}+\text{P}[/latex], which will then allow you to calculate the markup percentages.
Step 4: Apply any of the merchandising formulas from Formula 4.1a to Formula 4.5b to calculate the unknown variables required to solve the formulas. Your goal is to identify all required variables and then solve the original unknown variables from Step 1.
Things To Watch Out For
Before proceeding, take a few moments to review the various concepts and formulas covered earlier in this chapter. A critical and difficult skill is now at hand. As evident in Steps 2 through 4 of the solving process, you must use your problem-solving skills to figure out which formulas to use and in what order. Here are three suggestions to help you on your way:
- Analyze the question systematically.
- If you are unsure of how the pieces of the puzzle fit together, try substituting your known variables into the various formulas. You are looking for
- Any solvable formulas with only one unknown variable or
- Any pair of formulas with the same two unknowns, since you can solve this system using your algebraic skills of solving two linear equations with two unknowns (covered in Section 2.6).
- Merchandising has multiple steps. Think through the process. When you solve one equation for an unknown variable, determine how knowing that variable affects your ability to solve another formula. As mentioned in Step 3, there is usually a critical unknown variable. Once you determine the value of this variable, a domino effect allows you to solve any other remaining formulas
Example 4.5.1
A skateboard shop stocks a Tony Hawk Birdhouse Premium Complete Skateboard. Each skateboard costs [latex]\$45.46[/latex] and the store has overheads expenses of [latex]\$25.17[/latex] on each skateboard. The shop wants to sell each skateboard for an operating profit of [latex]\$10.55[/latex]. During a sale, it offers a markdown rate of [latex]10\%[/latex]. At the sale prices, calculate the store’s profit or loss.
Solution
Step 1: List what you know.
[latex]\begin{eqnarray*}C&=&\$45.46\;\\E&=&\$25.17\;\\P&=&\$10.55\;\\D&=&25\%\end{eqnarray*}[/latex]
Write the unknowns: [latex]\$D,\;S,\;S_{red},\;P_{red}[/latex]
Step 2: Where can you find the information in known formulas?
Using Formula 4.3a ([latex]S=C+E+P[/latex]) will give us the selling price and the [latex]\$D[/latex].
[latex]\$D=0.10S[/latex]
Using Formula 4.4c, [latex]S_{red}=S-D[/latex], we can find the reduced sale price.
Using Formula 4.5a, [latex]P_{red}=S_{red}-C-E[/latex], we can find the reduced profit.
Using Formula 4.5b, [latex]P_{red}=P-D[/latex], we can find the reduced profit.
Step 3: Where do you find the unknown variables.
Same as Step 2.
Step 4: Solve the Question: There are two methods to solve the question.
Method 1
[latex]\begin{eqnarray*}S&=&{\color{green}{C}}+{\color{blue}{E}}+{\color{purple}{P}}\\S&=&{\color{green}{\$45.46}}+{\color{blue}{\$25.17}}+{\color{purple}{\$10.55}}\\S&=&\$81.18\\\\D&=&0.10{\color{purple}{S}}\\D&=&0.10\times{\color{purple}{\$81.18}}\\D&=&\$8.12\\\\S_{red}&=&{\color{chocolate}{S}}-{\color{Magenta}{D}}\\S_{red}&=&{\color{chocolate}{\$81.18}}-{\color{Magenta}{\$8.12}}\\S_{red}&=&\$73.06\\\\P_{red}&=&{\color{red}{S_{red}}}-{\color{green}{C}}-{\color{blue}{E}}\\P_{red}&=&{\color{red}{\$73.06}}-{\color{green}{\$45.46}}-{\color{blue}{\$25.17}}\\P_{red}&=&\$2.43\end{eqnarray*}[/latex]
Method 2
|
Merchandising Calculation Table |
|||
|
|
Amount | Rate | |
|
|
on [latex]C[/latex] | On [latex]S[/latex] | |
| [latex]P[/latex] | $10.55 |
|
|
| [latex]+E[/latex] | $25.17 |
|
|
| [latex]M[/latex] | $35.72 |
|
|
| [latex]+C[/latex] | $45.46 | ||
| [latex]S[/latex] | $81.18 | ||
| [latex]-D[/latex] | $8.12 | 0.10 | |
| [latex]S_{red}[/latex] | $73.06 | ||
| ** [latex]{\color{blue}{-C}}[/latex] | $45.46 | ||
| **[latex]{\color{blue}{-E}}[/latex] | $25.17 | ||
| [latex]P_{red}[/latex] | $2.43 | ||
| **[latex]{\color{blue}{-BE}}[/latex] | |||
Step 5: Write as a statement.
At the sale price of [latex]\$73.06[/latex] the skateboard shop will make a profit of [latex]\$2.43[/latex].
Example 4.5.2
The Cycle Corner bought a bicycle for [latex]\$500[/latex], the overhead expense were [latex]20\%[/latex] on the cost, and the operating profit is [latex]30\%[/latex] on the cost. The bicycle is marked down by [latex]25\%[/latex] during a sale.
- What is the profit or loss on the reduced sale price?
- What is the amount of markup on sale price?
Solution
a.
Step 1: List what you know from the question.
[latex]\begin{eqnarray*}C&=&\$500\\E\;&=&0.20C\\P&=&0.30\;C\\D&=&.25S\end{eqnarray*}[/latex]
Write the unknowns: [latex]S,D,E,P,\text{ Markup on Sale Price}[/latex]
Step 2: Where can your find the information in known formulas?
Using Formula 4.3a, [latex]S=C+E+P[/latex], will give us the selling price.
Using Formula 4.4c, [latex]S_{red}=S-D[/latex], will give us the reduced sale price.
Using Formula 4.5a, [latex]P_{red}=S_{red}-C-E[/latex], will give us the reduced profit.
Using Formula 4.5b, [latex]P_{red}=P-D[/latex], will give us the reduced profit.
Step 3: Where do you find the unknown variables:
Same as Step 2.
Step 4: Solve the Question: There are two methods to solve the question.
Method 1
[latex]\begin{eqnarray*}{\color{green}{\text{Cost}}}&=&{\color{green}{\$500}}\\\$E&=&0.20(\$500)\\{\color{blue}{\$E}}&=&{\color{blue}{\$100}}\\\\\$P&=&0.30(\$500)\\{\color{red}{\$P}}&=&{\color{red}{\$150.00}}\\\\\text{Using Formula 4.3a: }S&=&{\color{green}{C}}+{\color{blue}{E}}+{\color{red}{P}}\\S&=&{\color{green}{\$500}}+{\color{blue}{\$100}}+{\color{red}{\$150.00}}\\{\color{purple}{S}}&=&{\color{purple}{\$750.00}}\\\\\$D&=&0.25{\color{purple}{S}}\\\$D&=&0.25({\color{purple}{\$750}})\\{\color{Magenta}{\$D}}&=&{\color{Magenta}{\$187.50}}\\\\S_{red}&=&{\color{purple}{S}}-{\color{Magenta}{D}}\\S_{red}&=&{\color{purple}{\$750.00}}-{\color{Magenta}{\$187.50}}\\{\color{Mahogany}{S_{red}}}&=&{\color{Mahogany}{\$562.50}}\\\\P_{red}&=&{\color{Mahogany}{S_{red}}}-{\color{green}{C}}-{\color{blue}{E}}\\P_{red}&=&{\color{Mahogany}{\$562.50}}-{\color{green}{\$500}}-{\color{blue}{\$100}}\\P_{red}&=&-\$37.50\end{eqnarray*}[/latex]
Method 2
|
Merchandising Calculation Table |
|||
|
|
Amount | Rate | |
|
|
on [latex]C[/latex] | On [latex]S[/latex] | |
| [latex]P[/latex] | $150.00 | 30% | |
| [latex]+E[/latex] | $100.00 | 20% | |
| [latex]M[/latex] | $250.00 |
|
|
| [latex]+C[/latex] | $500 | ||
| [latex]S[/latex] | $750.00 | ||
| [latex]-D[/latex] | $187.50 | 0.25 | |
| [latex]S_{red}[/latex] | $562.50 | ||
| ** [latex]{\color{blue}{-C}}[/latex] | $500 | ||
| **[latex]{\color{blue}{-E}}[/latex] | $100 | ||
| [latex]P_{red}[/latex] | -$37.50 | ||
| **[latex]{\color{blue}{-BE}}[/latex] | |||
b.
[latex]\begin{eqnarray*}\text{Markup on Sale Price}&=&S_{red}-C\\\text{Markup on Sale Price}&=&\$562.50-\$500\\\text{Markup on Sale Price}&=&\$62.50\end{eqnarray*}[/latex]
Step 5: Write as a statement:
At the sale price of [latex]\$562.50[/latex] the Cycle Corner will have a loss of [latex]\$37.50[/latex] and the Markup amount on the sale price is [latex]\$62.50[/latex].
Example 4.5.3
A manufacturer makes laptop computers at a cost of [latex]\$1794[/latex] per machine. The Company’s operating profit is [latex]20\%[/latex] on the selling price and the markup is [latex]35\%[/latex] on the selling price. During a computer trade show the company offered the computer at a discount of [latex]17.5\%[/latex].
- What is the selling price of the machine?
- At the [latex]17.5\%[/latex] discount did the company have a profit or a loss and how much?
- What should be the rate of markdown to sell the machines at the break-even price?
Solution
Step 1: List what you know.
[latex]\begin{eqnarray*}\text{Cost}\;(C)&=&\$1794\\\text{Profit}\;(P)&=&20\%\;\text{on selling price}\\\text{Markup}\;(M)&=&35\%\;\text{on Selling price}\end{eqnarray*}[/latex]
Write the unknowns: [latex]D,\;S,\;M,\;P,\;S_{red}\;,\;P_{red}[/latex]
Step 2: Where can you find the information in known formulas?
Using Formula 4.3a, [latex]S=C+E+P[/latex], will give us the selling price.
Using Formula 4.3b, [latex]M=E+P[/latex], will give us the Markup.
Using Formula 4.4c, [latex]S_{red}=S-D[/latex], will give us the reduced sale price.
Using Formula 4.5a, [latex]P_{red}=S_{red}-C-E[/latex], will give us the reduced profit.
Using Formula 4.5b, [latex]P_{red}=P-D[/latex], will give us the reduced profit.
Step 3: Where do you find the unknown variables:
Same as Step 2.
Step 4: Solve the Question: There are two methods to solve the question.
a.
[latex]\begin{eqnarray*}\text{Selling Price}\\S&=&{\color{green}{C}}+{\color{red}{M}}\\S&=&{\color{green}{\$1794}}+{\color{red}{0.35S}}\\1S-0.35S&=&\$1794\\0.65S&=&\$1794\\{\color{blue}{S}}&=&{\color{blue}{\$2\text{,}760.00}}\end{eqnarray*}[/latex]
b. Profit or Loss
[latex]\begin{eqnarray*}\text{Markup}\\M&=&0.35S\\M&=&0.35(\$2760.00)\\{\color{red}{M}}&=&{\color{red}{\$966}}\\\\\text{Profit}\\P&=&0.20S\\P&=&0.20(\$2760)\\{\color{purple}{P}}&=&{\color{purple}{\$552}}\\\\\text{Expenses }\\E&=&M-P\\E&=&\$966-\$552\\{\color{blue}{E}}&=&{\color{blue}{\$414}}\\\\\text{Discount}\\D&=&0.175(\$2760)\\{\color{Magenta}{D}}&=&{\color{Magenta}{\$483}}\\\\\text{Selling Price Reduced}\\S_{red}&=&S-D\\S_{red}&=&\$2760-\$483\\{\color{Mahogany}{S_{red}}}&=&{\color{Mahogany}{\$2277}}\\\\\text{Reduced Profit}\\P_{red}&=&{\color{Mahogany}{S_{red}}}-{\color{green}{C}}-{\color{blue}{E}}\\P_{red}&=&{\color{Mahogany}{\$2277}}-{\color{green}{\$1794}}-{\color{blue}{\$414}}\\P_{red}&=&+\$69.00\\\end{eqnarray*}[/latex]
c. Rate of Markdown at Break-Even Price
Method 1
[latex]\begin{eqnarray*}\text{Break even is when C + E }\;\\BE&=&C+E\;\\BE&=&\$1794\;+\;\$414\;\\BE&=&\$2208.00\;\;\\\\\text{Markdown}\;(D)&=&\text{Selling Price}-BE\;\;\\\text{Markdown}\;(D)&=&\$2760\;-\;\$2208\\\text{Markdown}\;(D)&=&\$552\;\;\\\\\text{Markdown Rate}&=&\frac{\$552}{\$2760}\times100\%\;\\[1ex]\text{Markdown Rate}&=&20\%\end{eqnarray*}[/latex]
Method 2
|
Merchandising Calculation Table |
|||
|
|
Amount | Rate | |
|
|
on [latex]C[/latex] | On [latex]S[/latex] | |
| [latex]P[/latex] | $552 | 20% | |
| [latex]+E[/latex] | $414 | 15% | |
| [latex]M[/latex] | $966 |
|
35% |
| [latex]+C[/latex] | $1794 | ||
| [latex]S[/latex] | $2760 | ||
| [latex]-D[/latex] | -$483 | 17.5% | |
| [latex]S_{red}[/latex] | $2277 | ||
| ** [latex]{\color{blue}{-C}}[/latex] | -$1794 | ||
| **[latex]{\color{blue}{-E}}[/latex] | -$414 | ||
| [latex]P_{red}[/latex] | -$69.00 | ||
| **[latex]{\color{blue}{-BE}}[/latex] | |||
Step 5: Write a Statement
The selling price of the computer is [latex]\$2760[/latex] and with a [latex]17.5\%[/latex] discount at the trade show, there is a profit of [latex]\$69.00[/latex]. The rate of markdown if the computer is sold at the break-even price is [latex]20\%[/latex].
Example 4.5.4
Carlton Printers manufactures and sells printers for [latex]\$108.50[/latex] each. The operating profit is [latex]30\%[/latex] on cost and markup is [latex]75\%[/latex] on cost. During the back to school sale the printer is offered at a rate of markdown that will provide a profit of [latex]\$5.58[/latex] per printer.
- How much does it cost Carlton Printers to manufacture each printer?
- Calculate the rate of markdown offered during a sale if a profit of [latex]\$5.58[/latex] is made in profit on each printer.
- What should be the rate of markdown offered if the printer is selling at its cost price?
Solution
Step 1: List what you know.
[latex]\begin{eqnarray*}S&=&\$108.50\\P&=&0.30C\\M&=&0.75C\end{eqnarray*}[/latex]
Step 2: Where can you find the information in known formulas?
Using Formula 4.3a, [latex]S=C+E+P[/latex], will give us the selling price.
Using Formula 4.3b, [latex]M=E+P[/latex], will give us the Markup.
Using Formula 4.4c, [latex]S_{red}=S-D[/latex], will give us the reduced sale price.
Using Formula 4.5a, [latex]P_{red}=S_{red}-C-E[/latex], will give us the reduced profit.
Using Formula 4.5b, [latex]P_{red}=P-D[/latex], will give us the reduced profit.
Step 3: Where do you find the unknown variables:
Same as Step 2.
Step 4: Solve the questions.
a. Cost of the Printer
[latex]\begin{eqnarray*}S&=&\$108.50\\P&=&0.30C\\M&=&0.75C\\\\S&=&C+M\\\$108.50&=&C+0.75C\\\$108.50&=&1.75C\\C&=&\$62.00\;\text{Each printer cost is \$62.00}\end{eqnarray*}[/latex]
b. Rate of Markdown with [latex]\$5.58[/latex] in profit after discount.
[latex]\begin{eqnarray*}\;M&=&E+P\;\;\\0.75C&=&E\;+\;.30C\;\\E&=&0.45C\;\\E&=&0.45(\$62.00)\;\;\\E&=&\$27.90\\\\P_{red}&=&S_{red}-C-E\;\\\$5.58&=&S_{red}-\$62.00-\$27.90\;\\S_{red}&=&95.48\\\\S_{red}&=&S-D\;\;\\95.48&=&\$108.50-D\;\;\\D&=&\$13.02\\\\\text{Rate of Markdown}&=&\frac{\$13.02}{\$108.50}\times100\%\\[1ex]\text{Rate of Markdown}&=&12\%\end{eqnarray*}[/latex]
c. Rate of Markdown with a price at cost.
Method 1
[latex]\begin{eqnarray*}S_{red}&=&C=\$62.00\\S_{red}&=&S-D\\D&=&S-S_{red}\\D&=&\$108.50-\$62.00\\D&=&\$46.50\\\\\text{Rate of Markdown}&=&\frac{\$46.50}{\$108.50}\times100\%\\[1ex]\text{Rate of Markdown}&=&42.86\%\end{eqnarray*}[/latex]
Method 2
|
Merchandising Calculation Table |
|||
|
|
Amount | Rate | |
|
|
on [latex]C[/latex] | On [latex]S[/latex] | |
| [latex]P[/latex] | $18.60 | 30% | |
| [latex]+E[/latex] | $27.90 | ||
| [latex]M[/latex] | $46.50 | 75% | |
| [latex]+C[/latex] | $62.00 | ||
| [latex]S[/latex] | $108.50 | ||
| [latex]-D[/latex] | $13.02 | 12% | |
| [latex]S_{red}[/latex] | $95.48 | ||
| ** [latex]{\color{blue}{-C}}[/latex] | -$62.00 | ||
| **[latex]{\color{blue}{-E}}[/latex] | -$27.90 | ||
| [latex]P_{red}[/latex] | $5.58 | ||
| **[latex]{\color{blue}{-BE}}[/latex] | |||
Step 5: Write a Statement
The cost for each printer for Carlton Printers is [latex]\$62.00[/latex]. With a profit of [latex]\$5.58[/latex] per printer the rate of markdown would be [latex]12\%[/latex].
Example 4.5.5
A retailer of electronic goods, purchases [latex]1000[/latex] TVs from a distributor after trade discounts of [latex]10\%[/latex] and [latex]8\%[/latex] on the list price of [latex]\$600[/latex] per TV. The retailer then marks up the TVs by [latex]55\%[/latex] on selling price and sells [latex]660[/latex] units at the regular selling price. During a sale, they offer a markdown of [latex]10\%[/latex] and sell another [latex]300[/latex] units at that sale price. They finally sell the remaining units at the break-even price. Overhead expenses for the retailer are [latex]20\%[/latex] of the selling price.
- What is the selling price of the [latex]660[/latex] units sold?
- What was the price of the [latex]300[/latex] units sold?
- What is the break-even price at which the final units were sold?
- What is the total profit or loss from the sale of the [latex]1000[/latex] units?
Solution
Step 1: List what you know.
[latex]\begin{eqnarray*}L&=&\$600\\M&=&0.55S\\D&=&0.10S\\E&=&0.20S\end{eqnarray*}[/latex]
Step 2: Where can you find the information in known formulas?
Using Formula 4.1d, [latex]$D=L \times (1-d)(1-d)...[/latex], will give us the discount amount.
Using Formula 4.3c, [latex]S=C+M[/latex], will give us the selling price, [latex]M[/latex] and [latex]P[/latex].
Using Formula 4.4b, [latex]$M=S\times d[/latex], will give us the Markdown amount.
Using Formula 4.4c, [latex]S_{red}=S-D[/latex], will give us the reduced sale price.
Using Formula 4.5a, [latex]P_{red}=S_{red}-C-E[/latex], will give us the reduced profit.
Using Formula 4.5b, [latex]P_{red}=P-D[/latex], will give us the reduced profit.
Step 3: Where do you find the unknown variables?
Same as Step 2.
Step 4: Solve the questions.
Method 1
a.
[latex]\begin{eqnarray*}\text{Discount Amount}&=&L\;x\;(1-d)(1-d)\dots\\\text{Discount Amount}&=&\$600(1-0.10)(1-0.08)\\\text{Discount Amount}&=&\$600(0.9)(0.92)\\\text{Discount Amount}&=&\$496.80\;\\\\S&=&C+M\;\\S&=&\$496.80+0.55S\;\\0.45S&=&\$496.80\;\\S&=&\$1104.00\;\\\text{660 units sold at \$1104.00}\end{eqnarray*}[/latex]
b.
[latex]\begin{eqnarray*}\text{Markdown Amount}&=&S\times d\;\\\text{Markdown Amount}&=&\$1104.00\times(0.10))\\\text{Markdown Amount}&=&\$110.40\\\\S_{red}&=&S-D\;\\S&=&\$1104.00-\$110.40\;\\S&=&\$993.60\\\text{300 Units sold at \$993.00}\end{eqnarray*}[/latex]
c.
[latex]\begin{eqnarray*}BE\;\text{price}&=&C+E\;\;\\BE\;\text{price}&=&\$496.80+(0.20\times\$1104.00)\\BE\;\text{price}&=&\$496.80+\$220.80\\BE\;\text{price}&=&\$717.60\;\end{eqnarray*}[/latex]
The [latex]BE[/latex] price at which the remaining TVs were sold is [latex]\$717.60[/latex].
d. Profits from all TVs.
[latex]\text{Total cost of 1000 Units}=1000\times 496.80 = \$496,800.00[/latex]
[latex]\text{Total operating expenses}=1000\times 0.20 \times \$1104.00 = \$220,800.00[/latex]
[latex]\text{Total Selling price}=(660 \times \$1104.00) + (300 \times \$993.00) + (40 \times \$717.60)\\\text{Total Selling price}= \$1,055,424.00[/latex]
[latex]\begin{eqnarray*}\text{Total Profit}&=&{\color{red}{S}}-{\color{green}{C}}-{\color{blue}{E}}\\\text{Total Profit}&=&{\color{red}{\$1\text{,}055\text{,}424.00}}-{\color{green}{\$496\text{,}800.00}}-{\color{blue}{\$220\text{,}800.00}}\\\text{Total Profit}&=&\$337,824.00\end{eqnarray*}[/latex]
Method 2
|
Merchandising Calculation Table |
|||
|
|
Amount | Rate | |
|
|
on [latex]C[/latex] | On [latex]S[/latex] | |
| [latex]P[/latex] | [latex]{\color{red}{\boxed{\$386.40}}}[/latex] | ||
| [latex]+E[/latex] | $220.80 | 20% | |
| [latex]M[/latex] | $607.20 | 55% | |
| [latex]+C[/latex] | $496.80 | ||
| [latex]S[/latex] | $1104.00 | ||
| [latex]-D[/latex] | $110.40 | 10% | |
| [latex]S_{red}[/latex] | $993.60 | ||
| ** [latex]{\color{blue}{-C}}[/latex] | -$496.80 | ||
| **[latex]{\color{blue}{-E}}[/latex] | -$220.80 | ||
| [latex]P_{red}[/latex] | [latex]\color[rgb]{1.0, 0.0, 0.0}\boxed{\$276.00}[/latex] | ||
| **[latex]{\color{blue}{-BE}}[/latex]
*Boxed values indicate profit for each unit sold at regular price (660 units) |
|||
[latex]\begin{eqnarray*}\text{Total Profit}&=&(600\times\$386.40)\;+\;(300\times\$276.00)\;+\;(40\times00.00)\\\text{Total Profit}&=&\$337,824.00\end{eqnarray*}[/latex]
Step 5: Write a Statement
The selling price of the [latex]660[/latex] units sold at regular price was [latex]\$1104.00[/latex]. The sale price of the [latex]300[/latex] units sold was [latex]\$993.60[/latex]. The break-even price of the remaining [latex]40[/latex] units sold was [latex]\$717.60[/latex]. Finally, the total profit made from the sale of all [latex]1000[/latex] TVs was [latex]\$337,824.00[/latex].
Section 4.5 Exercises
Round all money to two decimals and percentages to four decimals for each of the following exercises.
- Calculate the missing values for the table below:
|
|
Cost |
Amount of Markup |
Selling Price |
Operating Profit |
Overhead Expenses |
Rate of Markup on Cost |
Rate of Markup on Selling Price |
Rate of Markdown |
Reduced Selling Price |
Reduced Profit |
|
a. |
$12.50 |
? |
$18.50 |
$4.00 |
? |
? |
? |
? |
? |
-$1.30 |
|
b. |
? |
$180.50 |
$750.50 |
? |
$45.75 |
? |
? |
? |
$710.50 |
? |
|
c. |
? |
? |
$12,400 |
? |
$1280.50 |
? |
23% |
9% |
? |
? |
|
d. |
? |
? |
? |
$0.25 |
? |
30% |
? |
5.5% |
? |
? |
|
e. |
? |
? |
? |
$40.50 |
$80.50 |
? |
? |
5% |
? |
? |
- Ziggys skates purchases ice skates for [latex]\$30[/latex] each pair and sells them at a regular price of [latex]\$42[/latex] each pair.
- If the profit made is [latex]\$5.25[/latex] per pair of ice skates, calculate the overhead expense per pair.
- If the discount offered during a Holiday Sale is [latex]20\%[/latex], calculate the reduced selling price and the profits or loss made on the sale of each pair.
- Belanger Acoustics purchased acoustic guitars for [latex]\$80[/latex] each and has marked them up by [latex]20\%[/latex] on cost. The overhead expenses were [latex]10\%[/latex] on cost.
- Calculate the regular selling price of each guitar and the profit made.
- If Belanger decides to offer a markdown of [latex]5\%[/latex] what would be the reduced selling price and profit or loss they would make on the sale of each guitar?
- Julia makes a [latex]10\%[/latex] profit on the cost of T shirts, which she purchases at [latex]\$15.00[/latex] each. The overhead expenses are [latex]25\%[/latex] on cost. During a slae, she maked the T shirts down by [latex]10\%[/latex].
- What is the profit or loss on the sale of this item?
- What is the amount of markup on the sale price of the item?
- Guilherme was in the business of purchasing painting from Brazil and selling them in Toronto at his shop. On one shipment listed at [latex]\$2400[/latex], he received trade discounts of [latex]10\%[/latex], [latex]8\%[/latex], and [latex]6\%[/latex]. The overhead expenses were [latex]15\%[/latex] of his costs and he wanted to make an operating profit of [latex]20\%[/latex] on cost.
- Calculate the regular selling price of the painting.
- Calculate the loss or profit he will make if he decides to markdown the selling prices by [latex]15\%[/latex].
- Calculate the maximum amount of markdown that he can offer so that he breaks even on the sale.
- Juanita purchased designer purses for [latex]\$242.88[/latex] each, less [latex]12\%[/latex] and [latex]8\%[/latex]. The markup is [latex]35\%[/latex] on selling price and the operating profit is [latex]15\%[/latex] on cost. During a sale , the designer purses were marked down to [latex]\$260.00[/latex].
- What was the regular selling price?
- What was the rate of markdown?
- At the sale price, what was the profit of loss?
- The regular selling price of cell phones at a store is [latex]\$125[/latex] each. During a sale, it was sold at a markdown of [latex]45\%[/latex]. Calculate the profit or loss made on the sale of the cell phone if the break-even price is [latex]\$75[/latex].
- A retailer purchased shirts for [latex]\$50[/latex] each, less [latex]10\%[/latex]. The retailer has a markup of [latex]20\%[/latex] on selling price and an operating profit of [latex]10\%[/latex] on cost. During a sale, the shirts were marked down and sold at break-even price.
- What was the regular selling price of each shirt?
- What was the sale price?
- What was the rate of markdown offered during the sale?
Solutions
- a. [latex]\$6.00[/latex], [latex]\$2.00[/latex], [latex]48\%[/latex], [latex]32.43\%[/latex], [latex]28.65\%[/latex], [latex]\$13.20[/latex];
b. [latex]\$570.00[/latex], [latex]\$134.75[/latex], [latex]31.67\%[/latex], [latex]24.05\%[/latex], [latex]5.33\%[/latex], [latex]\$94.75[/latex];
c. [latex]\$9548[/latex], [latex]\$2852[/latex], [latex]\$1571.50[/latex], [latex]29.87\%[/latex], [latex]\$11,284[/latex], [latex]\$455.50[/latex];
d. [latex]\$0.45[/latex], [latex]\$1.95[/latex], [latex]\$0.20[/latex], [latex]23.08\%[/latex], [latex]\$1.84[/latex], [latex]\$0.14[/latex] - a. [latex]\$6.75[/latex]; b. [latex]\$33.60[/latex] and [latex]-\$3.15[/latex]
- a. [latex]\$96.00[/latex], [latex]\$8.00[/latex]; b. [latex]\$91.20[/latex], [latex]\$3.20[/latex]
- a. [latex]-\$0.53[/latex]; b. [latex]\$3.22[/latex]
- a. [latex]\$2521.76[/latex]; b. [latex]3.52\%[/latex]; c. [latex]25.93\%[/latex]
- a. [latex]\$302.52[/latex]; b. [latex]14.06\%[/latex]; c. [latex]-\$13.02[/latex]
- [latex]-\$6.25[/latex]
- a. [latex]\$56.25[/latex]; b. [latex]\$51.75[/latex]; c. [latex]8\%[/latex]
THE FOLLOWING LATEX CODE IS FOR FORMULA TOOLTIP ACCESSIBILITY. NEITHER THE CODE NOR THIS MESSAGE WILL DISPLAY IN BROWSER.[latex]\text{M}\$=\text{E}+\text{P}[/latex][latex]\begin{align*}MoC\%=\frac{\text{M}\$}{\text{C}}\times 100\end{align*}[/latex][latex]\begin{align*}\text{MoS}\%=\frac{\text{M}\$}{\text{S}}\times 100\end{align*}[/latex]
Attribution
"6.4: Merchandising" from Business Math: A Step-by-Step Handbook (2021B) by J. Olivier and Lyryx Learning Inc. through a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License unless otherwise noted.

