3.7: Exchange Rates and Currency Exchange
Formula & Symbol Hub
For this section you will need the following:
Symbols Used
- [latex]S=[/latex] Selling price
- [latex]C=[/latex] Cost
- [latex]E=[/latex] Expenses
- [latex]P=[/latex] Profit
Formulas Used
-
Formula 3.7 - Currency Exchange
[latex]\text{Desired Currency}=\text{Exchange Rate}\times\text{Current Currency}[/latex]
-
Formula 3.1b - Rate, Portion, and Base
[latex]\begin{align*}\text{Rate}=\frac{\text{Portion}}{\text{Base}}\end{align*}[/latex]
-
Formula 4.3a - Selling Price of a Product (see Section 4.3)
[latex]\text{S}=\text{C}+\text{E}+\text{P}[/latex]
Introduction
You have set aside [latex]\$6,000[/latex] in Canadian funds toward hostel costs during a long backpacking trip through the United States, Mexico, and Europe. After searching on the Internet, you decide to use Hotwire.com to reserve your hostel rooms. The website quotes you the following amounts for each country: [latex]1,980[/latex] US dollars, [latex]21,675[/latex] Mexican pesos, and [latex]1,400[/latex] euros. Have you allocated enough money to cover these costs?
Whether you are a consumer backpacking around the world on distant vacations, investing in international securities, or shopping online at global Internet sites, you must pay for your purchases in local currencies out of your Canadian currency accounts. Businesses are no different as they export and import products to and from other countries. With outsourcing on the rise, it is also common for business services such as call centres and advertising agencies to be located abroad along with manufacturing facilities. Large-scale companies may have operations in several countries throughout the world.
All of these transactions and operations require the conversion of Canadian currency to a foreign currency or vice versa. This section shows you the basics of currency conversion rates and then explores finer details such as charges for currency conversion and what happens when one currency gets stronger or weaker relative to another.
Exchange Rates
An exchange rate between two currencies is defined as the number of units of a foreign currency that are bought with one unit of the domestic currency, or vice versa. Since two currencies are involved in every transaction, two published exchange rates are available. Let's use Canada and the United States to illustrate this concept.
- The first exchange rate indicates what one dollar of Canada's currency becomes in US currency.
- The second exchange rate indicates what one dollar of US currency becomes in Canadian currency.
These two exchange rates allow Canadians to determine how many US dollars their money can buy and vice versa. These currency rates have an inverse relationship to one another: if [latex]1[/latex] Canadian dollar equals [latex]0.80[/latex] US dollars, then [latex]1[/latex] US dollar equals [latex]\frac{1}{\$0.80}=1.25[/latex] Canadian dollars.
Most Canadian daily and business newspapers publish exchange rates in their financial sections. Although exchange rates are published in a variety of ways, a currency cross-rate table, like the table below, is most common. Note that exchange rates fluctuate all of the time as currencies are actively traded in exchange markets. Therefore, any published table needs to indicate the date and time at which the rates were determined. Also note that the cells where the same currency appears show no published rate as you never need to convert from Canadian dollars to Canadian dollars!
| Per C$ | Per US$ | Per € | Per ¥ | Per MXN$ | Per AU$ | |
|---|---|---|---|---|---|---|
| Canadian Dollar (C$) | 0.9787 | 1.4012 | 0.0122 | 0.0823 | 1.0360 | |
| US Dollar (US$) | 1.0218 | 1.4317 | 0.0125 | 0.0841 | 1.0585 | |
| Euro (€) | 0.7137 | 0.6985 | 0.0087 | 0.0588 | 0.7394 | |
| Japanese Yen (¥) | 82.0233 | 80.2765 | 114.9287 | 6.7540 | 84.9747 | |
| Mexican Peso (MXN$) | 12.1445 | 11.8859 | 17.0165 | 0.1481 | 12.5814 | |
| Australian Dollar (AU$) | 0.9652 | 0.9447 | 1.3525 | 0.0118 | 0.0795 |
In the table, all exchange rates have been rounded to four decimals. In true exchange markets, most exchange rates are expressed in [latex]10[/latex] decimals or more such that currency exchanges in larger denominations are precisely performed. For the purposes of this textbook, we will use a four decimal standard to simplify the calculations while still illustrating the principles of currency exchange.
Technically, only half of the table is needed, since one side of the diagonal line is nothing more than the inverse of the other. For example, the euro is [latex]0.7137[/latex] per C$ on the bottom of the diagonal. The inverse, or [latex]\frac{1}{0.7137}=1.4011[/latex] per €, is what is listed on top of the diagonal (the difference of [latex]0.0001[/latex] is due to rounding to four decimals).
The formula is yet again another adaptation of Formula 3.1b[latex]\begin{align*}\text{Rate}=\frac{\text{Portion}}{\text{Base}}\end{align*}[/latex] on Rate, Portion, and Base. Formula 3.7 expresses this relationship in the language of currency exchange.
[latex]\boxed{3.7}[/latex] Currency Exchange
[latex]\color{red}{\text{Desired Currency}}\color{black}{\text{ is what you are converting to:}}[/latex] In Formula 3.1b[latex]\begin{align*}\text{Rate}=\frac{\text{Portion}}{\text{Base}}\end{align*}[/latex], the desired currency represents the portion. This is what your money is worth in the other currency.
[latex]\color{blue}{\text{Exchange Rate}}\color{black}{\text{ is per unit of Current Currency:}}[/latex] In Formula 3.1b[latex]\begin{align*}\text{Rate}=\frac{\text{Portion}}{\text{Base}}\end{align*}[/latex], the exchange rate represents the rate, which is the current exchange rate per currency unit in which your money is currently valued. Looking at a Cross-Rate table, find the column that represents your existing currency and then cross-tabulate this column with the row for the desired currency (so you have desired currency per current currency). For example, if you have one euro that you want to convert into yen, locate the euro column and the yen row. The exchange rate is [latex]131.5789[/latex]. It is critical that both the exchange rate and current currency always be expressed in the same unit of currency type.
[latex]\color{green}{\text{Current Currency}}\color{black}{\text{ is what you are converting from:}}[/latex] In Formula 3.1b[latex]\begin{align*}\text{Rate}=\frac{\text{Portion}}{\text{Base}}\end{align*}[/latex], the current currency represents the base, which is the amount of money (number of units) in your existing currency.
Key Takeaways
Currencies, exchange rates, and currency cross-tables all raise issues regarding decimals and financial fees.
- Decimals in Currencies. Not all currencies in the world have decimals. Here in North America, MXN$, US$, and C$ have two decimals. Mexicans call those decimals centavos while Canadians and Americans call them cents. Australia and the European countries using the euro also have cents. However, the Japanese yen does not have any decimals in its currency. If you are unsure about the usage of decimals, perform a quick Internet search to clarify the issue.
- Financial Fees. Technically, the rates in a cross-rate table are known as mid-rates. A mid-rate is an exchange rate that does not involve or provide for any charges for currency conversion. When you convert currencies, you need to involve a financial organization, which will charge for its services.
- Sell Rates. When you go to a bank and convert your domestic money to a foreign currency, the bank charges you a sell rate, which is the rate at which a foreign currency is sold. When you exchange your money, think of this much like a purchase at a store—the bank's product is the foreign currency and the price it charges is marked up to its selling price. The sell rate is always higher than the mid-rate in terms of C$ per unit of foreign currency and thus is always lower than the mid-rate in terms of foreign currency per unit of C$. For example, the exchange rate of C$ per US$ is [latex]0.9787[/latex] (you always look up the “per currency” column that you are purchasing). This means it will cost you [latex]\text{C}\$0.9787[/latex] to purchase [latex]\text{US}\$1.00[/latex]. The bank, though, will sell you this money for a sell rate that is higher, say [latex]\$0.9987[/latex]. This means it will cost you an extra [latex]\text{C}\$0.02[/latex] per US$ to exchange the money. That [latex]$0.02[/latex] difference is the fee from the bank for its services, and it is how the bank makes a profit on the transaction.
- Buy Rates. When you go to a bank and convert your foreign currency back into your domestic money, the bank charges you a buy rate, which is the rate at which a foreign currency is purchased. The buy rate is always lower than the mid-rate in terms of C$ per unit of foreign currency and thus is always higher than the mid-rate in terms of foreign currency per unit of C$. Using the same example as above, if you want to take your [latex]\text{US}\$1.00[/latex] to the bank and convert it back to Canadian funds, the bank charges you a buy rate that is lower, say [latex]\$0.9587[/latex]. In other words, you receive [latex]\text{C}\$0.02[/latex] less per US$. Again, the [latex]\$0.02[/latex] difference is the bank's fee for making the currency exchange on your behalf.
HOW TO
Perform a Currency Exchange
Follow these steps when performing a currency exchange:
Step 1: Identify all known variables. Specifically, identify the currency associated with any amounts. You also require the mid-rate. If buy rates and sell rates are involved, identify how these rates are calculated.
Step 2: If there are no buy or sell rates, skip this step. If buy and sell rates are involved, calculate these rates in the manner specified by the financial institution.
Step 3: Apply Formula 3.7[latex]\text{Desired Currency}=\text{Exchange Rate}\times\text{Current Currency}[/latex] using the appropriate mid-rate, buy rate, or sell rate to convert currencies.
This section opened with your backpacking vacation to the United States, Mexico, and Europe, for which you were quoted prices of [latex]\text{US}\$1,980[/latex], [latex]\text{MXN}\$21,675[/latex], and [latex]\text{€}1,400[/latex] for hostels. Assume all purchases are made with your credit card and that your credit card company charges [latex]2.5\%[/latex] on all currency exchanges. Can your [latex]\text{C}\$6,000[/latex] budget cover these costs?
Step 1: There are three currency amounts: [latex]\text{US}\$1,980[/latex], [latex]\text{MXN}\$21,675[/latex], and [latex]\text{€}1,400[/latex]. Using the cross-rate table, the Canadian exchange mid-rate per unit of each of these currencies is [latex]\text{US}\$0.9787[/latex], [latex]\text{MXN}\$0.0823[/latex], and [latex]\text{€}1.4012[/latex].
Step 2: Calculate the buy rates (since you are converting foreign currency into domestic currency) for each currency:
[latex]\text{US}\$=0.9787(1.025)=1.0032[/latex]
[latex]\text{MXN}\$=0.0823(1.025)=0.0844[/latex]
[latex]\text{€}=1.4012(1.025)= 1.4362[/latex]
Step 3: Apply Formula 3.7
([latex]\text{Desired Currency}=\text{Exchange Rate}\times\text{Current Currency}[/latex])
to each of these currencies:
[latex]\text{US\$: Desired Currency}=\text{US}\$1,980\times 1.0032=\text{C}\$1,986.34[/latex]
[latex]\text{MXN\$: Desired Currency}=\text{MXN}\$21,675\times 0.0844=\text{C}\$1,829.37[/latex]
[latex]\text{€: Desired Currency}=\text{€}1,400\times 1.4362=\text{C}\$2,010.68[/latex]
Putting the three amounts together, your total hostel bill is:
[latex]\$1,986.34+\$1,829.37+\$2,010.68=\$5,826.39[/latex]
Because this is under budget by [latex]\$173.61[/latex], all is well with your vacation plans.
Things To Watch Out For
When working with currency exchange, probably the trickiest element is that you have to choose one of two inverse exchange rates depending on which way the money conversion is taking place. In any currency situation, it is important that you take the time to understand the basis on which the currency rate is being expressed. Typically, exchange rates are expressed on a per-unit basis in the country's domestic currency. For example, Canadians express the US dollar exchange rate on a per C$ basis. From the cross-rate table, that exchange rate is [latex]1.0218[/latex]. In contrast, Americans express the Canadian dollar exchange rate on a per US$ basis, or [latex]0.9787[/latex].
 Paths To Success
Paths To Success
Let the buyer beware when it comes to international transactions. If you have ever purchased and returned an item to an international seller, you may have noticed that you did not receive all of your money back. For most consumers, international purchases are made via credit cards. What most consumers do not know is that the credit card companies do in fact use buy and sell rates that typically charge [latex]2.5\%[/latex] of the exchange rate when both buying and selling.
For example, if you purchase a [latex]\text{US}\$2,000[/latex] item at the rates listed in the cross-rate table, your credit card is charged [latex]$2,000\times 0.9787(1.025)=\$2,006.40[/latex]. If you return an item you do not want, your credit card is refunded [latex]\$2,000\times 0.9787(0.975)=\$1,908.40[/latex]. In other words, you are out [latex]\$2,006.40−\$1,908.40=\$98[/latex]! This amount represents your credit card company's charge for the currency conversion—a whopping [latex]4.9\%[/latex] of your purchase price!
Try It
1) In each of the following situations and using the cross-rate table, determine on a strictly numerical basis whether you would have more or fewer units of the target currency than of the original currency. You want to convert:
- C$ into US$
- AU$ into MXN$
- MXN$ into ¥
- C$ into €
Solution
- Less, since [latex]\text{CAD}\$1[/latex] becomes [latex]\text{USD}\$0.8118[/latex]
- More, since [latex]\text{AUD}\$1[/latex] becomes [latex]\text{MXN}\$14.8810[/latex]
- More, since [latex]\text{MXN}\$1[/latex] becomes [latex]\text{¥}5.6180[/latex]
- Less, since [latex]\text{CAD}\$1[/latex] becomes [latex]\text{€}0.6841[/latex]
Example 3.7.1
Strictly using the mid-rates from the cross-rate table presented earlier, if you wanted to convert [latex]\text{C}\$1,500[/latex] into MXN$ for your spring break vacation in Cancun, Mexico, how many Mexican pesos would you have?
Solution
Step 1: What are we looking for?
Take Canadian currency and convert it into the desired Mexican currency.
Step 2: What do we already know?
The amount and the exchange rate are known:
[latex]\begin{align*}\text{Current Currency}&=\$1,500\\\text{Exchange Rate}&=12.1445\end{align*}[/latex]
Step 3: Make substitutions using the information known above.
No buy or sell rates are involved. Apply Formula 3.7:
[latex]\begin{align*}\text{Desired Currency}&=\text{Exchange Rate}\times\text{Current Currency}\\\text{Desired Currency}&=12.1445\times\$1,500\\\text{Desired Currency}&=\$18,216.75\end{align*}[/latex]
Step 4: Provide the information in a worded statement.
You have [latex]\$18,216.75[/latex] Mexican pesos available for your spring break vacation.
Example 3.7.2
A Mexican manufacturer imports its parts from Canada and assembles its product in Mexico, then exports some of the finished product back to Canada to sell at retail. Suppose the total cost of the imported parts, purchased and paid for in Canadian funds, is [latex]\text{C}\$5.50[/latex] per unit, assembly costs are [latex]\text{MXN}\$24.54[/latex] per unit, and expenses are [latex]\text{MXN}\$4.38[/latex] per unit. If the product is exported back to Canada at a selling price of [latex]\text{C}\$9.95[/latex] (for which its Canadian customers pay in Canadian funds), what is the total profit in Mexican pesos on [latex]10,000[/latex] units? The manufacturer's financial institution charges a sell rate [latex]2\%[/latex] higher than the mid-rate and has a buy rate that is [latex]3\%[/latex] lower than the mid-rate. Use the mid-rates from the cross-rate table.
Solution
Step 1: What are we looking for?
Calculate the total profit ([latex]P[/latex]) in MXN$ for the Mexican manufacturer. However, since money is being expressed in different currencies, you must first convert all amounts into Mexican pesos.
Step 2: What do we already know?
You know the costs, expenses, price, and mid-rate:
[latex]\begin{align*}\text{Cparts}&=10,000\times\text{C}\$5.50\\\text{Cparts}&=\text{C}\$55,000\\[2ex]\text{Cassembly}&=10,000\times\text{MXN}\$24.54\\\text{Cassembly}&=\text{MXN}\$245,400\\[2ex]E&=10,000\times\text{MXN}\$4.38\\E&=\text{MXN}\$43,800\\[2ex]S&=10,000\times\text{C}\$9.95\\S&=\text{C}\$99,500\\[2ex]\text{Mid-Rate}&=12.1445\;\text{per C}\\[2ex]\text{Sell Rate}&=2\%\;\text{higher}\\[2ex]\text{Buy Rate}&=3\%\;\text{lower}\end{align*}[/latex]
Note the mid-rate used is “per C$” since the manufacturer needs to purchase Canadian funds to pay its suppliers and also needs to sell its Canadian revenues to the bank.
Step 3: Make substitutions using the information known above.
Calculate the buy and sell rates.
[latex]\begin{align*}\text{Sell Rate}&=2\%\;\text{higher than mid-rate}\\\text{Sell Rate}&=12.1445(1+0.02)\\\text{Sell Rate}&=12.3874\\[2ex]\text{Buy Rate}&=3\%\;\text{lower than mid-rate}\\\text{Buy Rate}&=12.1445(1−0.03)\\\text{Buy Rate}&=11.7802\end{align*}[/latex]
Convert the purchase of the parts in C$ into MXN$ using the sell rate. Apply and adapt Formula 3.7[latex]\text{Desired Currency}=\text{Exchange Rate}\times\text{Current Currency}[/latex].
[latex]\begin{align*}\text{Cparts in MXN}\$&=12.3874\times\$55,000\\\text{Cparts in MXN}&=\$681,307\end{align*}[/latex]
Convert the sale of the product in C$ into MXN$ using the buy rate. Apply and adapt Formula 3.7[latex]\text{Desired Currency}=\text{Exchange Rate}\times\text{Current Currency}[/latex].
[latex]\begin{align*}\text{S in MXN}\$&=11.7802\times\$99,500\\\text{S in MXN}&=\$1,172,129.90\end{align*}[/latex]
All amounts are in MXN$. Apply Formula 4.3a[latex]\text{S}=\text{C}+\text{E}+\text{P}[/latex] (selling price of a product):
[latex]\begin{align*}S&=\text{Cparts}+\text{Cassembly}+E+P\\\$1,172,129.90&=\$681,307+\$245,400+\$43,800+P\\\$1,172,129.90&=\$970,507+P\\\$201,622.90&=P\end{align*}[/latex]
Step 4: Provide the information in a worded statement.
After converting all Canadian currency into Mexican pesos and factoring in the financial institution's buy and sell rates, the manufacturer realizes a profit of [latex]\$201,622.90[/latex] in Mexican pesos.
Currency Appreciation and Depreciation
An analyst on Global News is discussing how the Canadian dollar has strengthened against the US dollar. Your first reaction is that a strong Canadian dollar ought to be good thing, so hearing that this change might hurt Canada's exports, you wonder how that could be.
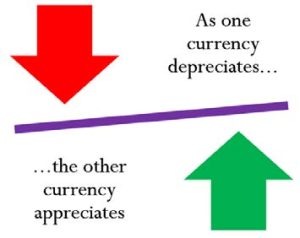
Currencies are actively traded in the international marketplace, which means that exchange rates are changing all the time. As such, exchange rates rise and decline. A currency appreciates (or strengthens) relative to another currency when it is able to purchase more of that other currency than it could previously. A currency depreciates (or weakens) relative to another currency when it is able to purchase less of that other currency than it could previously. Take a look at two examples illustrating these concepts:
- EXAMPLE 1: If [latex]\text{C}\$1[/latex] buys [latex]\text{US}\$1.02[/latex] and the exchange rate rises to [latex]\text{US}\$1.03[/latex], then your [latex]\text{C}\$1[/latex] purchases an additional penny of the US dollars. Therefore, the Canadian currency appreciates, or strengthens, relative to the US dollar.
- EXAMPLE 2: Similarly, if the exchange rate drops to [latex]\text{US}\$1.01[/latex], then your [latex]\text{C}\$1[/latex] purchases one less penny of the US dollars. Therefore, the Canadian currency depreciates, or weakens, relative to the US dollar.
These concepts are particularly important to international business and global economies. Generally speaking, when a currency appreciates it has a positive effect on imports from the other country because it costs less money than it used to for domestic companies to purchase the same amount of products from the other country. However, the currency appreciation tends to also have a negative effect on exports to other countries because it costs the foreign companies more money to purchase the same amount of products from the domestic companies.
Key Takeaways
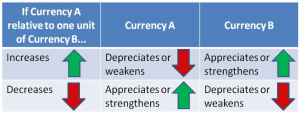
It is critical to observe that if currency A appreciates relative to currency B, then the opposite is true for currency B relative to currency A (currency B depreciates relative to currency A). The figure to the right illustrates this concept. Recalling Example 1 above, the Canadian currency appreciated, so the US currency depreciated. In Example 2, the Canadian currency depreciated, so the US currency appreciated.
HOW TO
Work with Currency Appreciation and Depreciation
When you work with currency appreciation or depreciation, you still use the same basic steps as before. The additional skill you require in the first step is to adjust an exchange rate appropriately based on how it has appreciated or depreciated.
Things To Watch Out For
It is very easy to confuse the two relative currencies, their values, and the concepts of appreciation and depreciation. For example, if the exchange rate increases between currency A relative to a unit of currency B, which exchange rate appreciated? If currency A has increased per unit of currency B, then it takes more money of currency A to buy one unit of currency B. As a result, currency B appreciates because a single unit of currency B can now buy more of currency A. For example, if the exchange rate is [latex]\text{US}\$1.0218[/latex] relative to [latex]\text{C}\$1[/latex] and it increases to [latex]\text{US}\$1.0318[/latex] relative to [latex]\text{C}\$1[/latex], then the Canadian dollar purchases one penny more. The figure helps you understand the relationships involved and provides a visual reminder of which direction everything is moving.
Try It
2) Answer the following:
- If the exchange rate in terms of US dollars per unit of euros increases, which currency weakened?
- If the Australian dollar weakens against the Canadian dollar, did the exchange rate increase or decrease in terms of Australian dollars per unit of Canadian dollars?
- If the exchange rate in terms of yen per unit of the Mexican pesos decreases, which currency weakened?
- If the British pound (£) appreciates against the US dollar, did the exchange rate increase or decrease in terms of pounds per unit of US dollars?
Solution
- US dollars
- Increase
- Mexican pesos
- Decrease
Example 3.7.3
A Canadian manufacturer requires parts from the United States. It purchases from its supplier in lots of [latex]100,000[/latex] units at a price of [latex]\text{US}\$7.25[/latex] per unit. Since the last time the manufacturer made a purchase, the Canadian dollar has appreciated [latex]0.0178[/latex] from the previous mid-rate of [latex]\text{US}\$1.0218[/latex] per C$. If the sell rate is [latex]1.5\%[/latex] above the mid-rate, how have the manufacturer's costs changed?
Solution
Step 1: What are we looking for?
Calculate the cost of the product both before and after the currency appreciation. The difference between the two numbers is the change in the manufacturer's costs.
Step 2: What do we already know?
The following purchase and exchange rates are known:
[latex]\begin{align*}\text{Current Currency}&=\text{Total Purchase}\\\text{Current Currency}&=100,000\times\$7.25\\\text{Current Currency}&=\text{US}\$725,000\\[2ex]\text{Mid-Rate}&=1.0218\;\text{per C\$}\\[2ex]\text{Sell Rate}&=1.5\%\;\text{higher}\\[2ex]\text{Canadian appreciation}&=0.0178\end{align*}[/latex]
Step 3: Make substitutions using the information known above.
Calculate the old and new sell rates, factoring in the currency appreciation. Notice that the Current Currency is in US dollars but the sell rates are per Canadian dollar. You will need to invert the rates so that the exchange rate is expressed per US dollar to match the Current Currency.
[latex]\begin{align*}\text{Previous Sell Rate}&=1.0218\times(1+0.015)\\\text{Previous Sell Rate}&= 1.0371\;\text{per C}\$\\[1ex]\text{Previous Sell Rate}&=\frac{1}{1.0371}\\[1ex]\text{Previous Sell Rate}&=0.9642\;\text{per US}\$\end{align*}[/latex]
If the Canadian dollar has appreciated, it buys more US dollars per C$. Therefore,
[latex]\begin{align*}\text{New Sell Rate}&=(1.0218+0.0178)\times(1+0.015)\\\text{New Sell Rate}&=1.0552\;\text{per C}\$\\[1ex]\text{New Sell Rate}&=\frac{1}{1.0552}\\[1ex]\text{New Sell Rate}&=0.9477\;\text{per US}\$\end{align*}[/latex]
Apply Formula 3.7[latex]\text{Desired Currency}=\text{Exchange Rate}\times\text{Current Currency}[/latex] for each transaction.
[latex]\begin{align*}\text{Previous C}\$&=0.9642\times\$725,000\\\text{Previous C}&=\$699,045\\[2ex]\text{New C}\$&=0.9477\times\$725,000\\\text{New C}&=\$687,082.50\end{align*}[/latex]
Calculate the difference between the two numbers to determine the change in cost.
[latex]\begin{align*}\text{Change in Cost}&=\text{New C}\$−\text{Previous C}\$\\\text{Change in Cost}&=\$687,082.50−\$699,045\\\text{Change in Cost}&=−\$11,962.50\end{align*}[/latex]
Step 4: Provide the information in a worded statement.
The manufacturer has its input costs decrease by [latex]\$11,962.50[/latex] since [latex]\text{C}\$1[/latex] now purchases more US$.
Section 3.7 Exercises
Mechanics
For questions 1–6, use the mid-rates in the cross-rate table below to convert the current currency to the desired currency.
| Per C$ | Per US$ | Per € | Per ¥ | Per MXN$ | Per AU$ | |
|---|---|---|---|---|---|---|
| Canadian Dollar (C$) | 0.9787 | 1.4012 | 0.0122 | 0.0823 | 1.0360 | |
| US Dollar (US$) | 1.0218 | 1.4317 | 0.0125 | 0.0841 | 1.0585 | |
| Euro (€) | 0.7137 | 0.6985 | 0.0087 | 0.0588 | 0.7394 | |
| Japanese Yen (¥) | 82.0233 | 80.2765 | 114.9287 | 6.7540 | 84.9747 | |
| Mexican Peso (MXN$) | 12.1445 | 11.8859 | 17.0165 | 0.1481 | 12.5814 | |
| Australian Dollar (AU$) | 0.9652 | 0.9447 | 1.3525 | 0.0118 | 0.0795 |
| Current Currency | Desired Currency | |
| 1. | C$68,000 | US$ |
| 2. | ¥15,000,000 | € |
| 3. | AU$3,000 | MXN$ |
| 4. | US$180,000 | AU$ |
| 5. | €230,500 | C$ |
| 6. | MXN$1,300,000 | ¥ |
Solutions
- [latex]55,202.40\text{USD}[/latex]
- [latex]114,000\text{€}[/latex]
- [latex]44,643\text{MXN}[/latex]
- [latex]239,004\text{AUD}[/latex]
- [latex]336,944.90\text{CAD}[/latex]
- [latex]7,303,400\text{¥}[/latex]
Applications
- If the exchange rate is [latex]¥97.3422[/latex] per C$, what is the exchange rate for C$ per ¥?
- Procter & Gamble just received payment for a large export of Tide in the amount of [latex]275,000[/latex] Denmark kroner (DKK). If the exchange mid-rate is [latex]\text{C}\$0.1992[/latex] per DKK and the bank charges [latex]3\%[/latex] on its buy rates, how many Canadian dollars will Procter & Gamble receive?
- The exchange rate per US$ is [latex]\text{C}\$0.9863[/latex]. If the Canadian dollar depreciates by [latex]\$0.0421[/latex] per US$, how many more or less US$ is [latex]\text{C}\$12,500[/latex] able to purchase?
- Jack is heading home to visit his family in Great Britain and decided to stop at the airport kiosk to convert his money. He needs to convert [latex]\text{C}\$5,000[/latex] to British pounds (£). The exchange mid-rate per C$ is [latex]£0.5841[/latex]. The kiosk charges a commission of [latex]4.5\%[/latex] on the conversion, plus a flat fee of [latex]£5.00[/latex].
-
- How many pounds will Jack have?
- What is the percentage cost of his transaction?
-
- Yarianni is heading on a vacation. She converts her [latex]\text{C}\$4,000[/latex] into Chinese yuan renminbi (CNY) at a sell rate of [latex]\text{CNY}6.3802[/latex] per C$. While in China, she spends [latex]\text{CNY}14,000[/latex] of her money. At the airport, she converts her remaining money into Indian rupees (INR) at a sell rate of [latex]\text{INR}6.7803[/latex] per CNY. In India, she spends [latex]\text{INR}50,000[/latex]. When she returns home, she converts her INR back to C$ at a buy rate of [latex]\text{C}\$0.0231[/latex] per INR. How many Canadian dollars did she return with? Note that all currencies involved have two decimals.
- Elena is an international investor. Four years ago she purchased [latex]2,700[/latex] shares of a US firm at a price of [latex]\text{US}\$23.11[/latex] per share when the exchange rate was [latex]\text{US}\$0.7536[/latex] per C$. Today, she sold those shares at a price of [latex]\text{US}\$19.87[/latex] per share when the exchange rate was [latex]\text{US}\$1.0063[/latex] per C$. In Canadian dollars, determine how much money Elena earned or lost on her investment.
- International Traders regularly imports products from Hong Kong. If the exchange rate of C$ per Hong Kong dollar (HKD) is [latex]0.1378[/latex] and the Canadian dollar appreciates by [latex]\text{HKD}0.0128[/latex], by what amount would the cost of a [latex]\text{HKD}1,000,000[/latex] purchase increase or decrease in Canadian dollars for International Traders?
- Brian needs to purchase some Brazilian reals (BRL). He takes [latex]\text{C}\$7,500[/latex] to the bank and leaves the bank with [latex]\text{BRL}12,753.20[/latex]. If the exchange mid-rate per C$ is [latex]1.7621[/latex], determine the sell rate commission percentage (rounded to two decimals) charged by the bank.
Solutions
7. [latex]0.0103\;\text{CAD per ¥}[/latex]
8. [latex]53,130\;\text{CAD}[/latex]
9. Purchase [latex]\$518.75[/latex] less than before
10a. [latex]2,784\;\text{£}[/latex]
10b. [latex]4.6739\%[/latex]
11. [latex]649.44\;\text{CAD}[/latex]
12. Elena lost [latex]\$29,489.81[/latex] on her investment
13. The products cost [latex]\$12,800\;\text{CAD}[/latex] less than before
14. [latex]3.5\%[/latex]
Challenge, Critical Thinking, & Other Applications
- Fernando could purchase a [latex]55[/latex]" Samsung HDTV in Winnipeg, Manitoba, for [latex]\$2,999.99[/latex] plus taxes. Alternatively, he could head across the border on Black Friday and shop in Grand Forks, North Dakota, where the same product is selling for [latex]\text{US}\$2,499.99[/latex] (plus [latex]5\%[/latex] state sales tax and [latex]1.75\%[/latex] local sales tax) at Best Buy. He estimates he would incur [latex]\$65[/latex] in gasoline and vehicle wear and tear, [latex]\$130[/latex] in accommodations, and [latex]\$25[/latex] in food (all money in US$). He would make all purchases on his credit card, which uses the mid-rate plus [latex]2.5\%[/latex]. When returning across the border, he would have to pay in Canadian dollars the [latex]5\%[/latex] GST on the Canadian value of the HDTV not including taxes. Once home, he can then have the North Dakota government refund all taxes paid on the HDTV through their Canadian sales tax rebate program. For all currency exchanges, assume a mid-rate of [latex]\text{US}\$0.9222[/latex] per C$. Which alternative is Fernando's better choice and by how much?
- The current mid-rate is [latex]\text{C}\$1.5832[/latex] per €. Scotiabank has a sell rate of [latex]\text{C}\$1.6196[/latex] per € while an airport kiosk has a sell rate of \[latex]text{C}\$1.6544[/latex] per € plus a service charge of [latex]\text{C}\$4.75[/latex]. You need to purchase [latex]€800[/latex].
- Calculate the fee percentages charged by each financial institution. Round your answers to one decimal.
- Rounded to two decimals, what percentage more than Scotiabank is the airport kiosk charging on your purchase?
- Henri and Fran have retired and are considering two options for a two-month vacation in Europe. Their local Lethbridge travel agent is offering them an all-inclusive package deal at [latex]\text{C}\$7,975[/latex] per person. Alternatively, they can book their own flights for [latex]\text{C}\$1,425[/latex] per person, stay in Britain at a small apartment averaging [latex]£65[/latex] per night for [latex]30[/latex] days, and then in France for [latex]€70[/latex] average per night for [latex]30[/latex] days. Estimated groceries cost a total of [latex]£250[/latex] in Britain and [latex]€400[/latex] in France. They will need to purchase a Eurail pass for [latex]€986[/latex] each while they are there. The exchange rates are [latex]€0.6808[/latex] per C$ and [latex]£0.5062[/latex] per C$. Which alternative is their cheapest option and by how much in Canadian dollars?
- A Canadian manufacturer imports three parts from different countries. It assembles the three parts into a finished item that is then exported to the United States. Every transaction always involves [latex]25,000[/latex] units. Expenses average [latex]\$6.25[/latex] per unit.
| Component | Price per unit | Exchange rate last month per C$ | Exchange rate this month per C$ |
| Part A | ¥1,500 | ¥107.9420 | ¥108.9328 |
| Part B | AU$14.38 | AU$1.1319 | AU$1.0928 |
| Part C | €10.73 | €0.6808 | €0.6569 |
| Finished product for export | US$59.45 | US$1.0128 | US$1.0243 |
Considering currency fluctuations, calculate the change in the profit month-over-month in Canadian dollars for the Canadian manufacturer.
- In each of the following situations, convert the old amount to the new amount using the information provided.
| Old Amount | Old Exchange Rate per C$ | Exchange Rate Change | New Amount | |
| a. | US$625.00 | US$0.9255 | C$ appreciated by US$0.0213 | ? US$ |
| b. | €16,232.00 | €0.5839 | C$ depreciated by €0.0388 | ? € |
| c. | ¥156,500 | ¥93.4598 | C$ depreciated by ¥6.2582 | ? ¥ |
| d. | MXN$136,000 | MXN$13.5869 | C$ appreciated by MXN$0.4444 | ? MXN$ |
- Compare the following four situations and determine which one would result in the largest sum of money expressed in Canadian funds.
| Situation | Amount | Exchange Rate per C$ |
| a. | 65,204 Algerian dinars (DZD) | DZD65.5321 |
| b. | 1,807,852 Colombian pesos (COP) | COP1,781.1354 |
| c. | 3,692 Israeli new shekels (ILS) | ILS3.7672 |
| d. | 30,497 Thai baht (THB) | THB30.4208 |
Solutions
15. Buy in the U.S. to save [latex]\$196.60[/latex]
16a.Scotiabank’s sell rate fee is [latex]2.3\%[/latex]; The kiosk’s sell rate fee is [latex]4.5\%[/latex]
16b. The airport kiosk charges [latex]2.52\%[/latex] more than Scotiabank
17. Booking it themselves saves [latex]\$1,824.98[/latex]
18. Currency fluctuations have decreased profits by [latex]\$38,432.12[/latex]
19a. [latex]639.38\;\text{USD}[/latex]
19b. [latex]\text{€}15,153.19[/latex]
19c. [latex]\text{¥}146,024[/latex]
19d. [latex]140,447.70\;\text{MXN}[/latex]
20. [latex]\text{COP}=\$1,084.71\;\text{CAD}[/latex]
[latex]\begin{align*}\text{Rate}=\frac{\text{Portion}}{\text{Base}}\end{align*}[/latex]THE FOLLOWING LATEX CODE IS FOR FORMULA TOOLTIP ACCESSIBILITY. NEITHER THE CODE NOR THIS MESSAGE WILL DISPLAY IN BROWSER.[latex]\text{Desired Currency}=\text{Exchange Rate}\times\text{Current Currency}[/latex][latex]\begin{align*}\text{Rate}=\frac{\text{Portion}}{\text{Base}}\end{align*}[/latex][latex]\text{S}=\text{C}+\text{E}+\text{P}[/latex]
Attribution
“7.3: Exchange Rates and Currency Exchange” from Business Math: A Step-by-Step Handbook (2021B) by J. Olivier and Lyryx Learning Inc. through a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License unless otherwise noted.

