And so, to Calculations

Stephen Marsh

And so, to Calculations

Introduction

In the last chapter we looked at a continuum for trust, which allowed us to do some really neat thinking about how it kind of works, especially for computational systems. The behaviour is pretty close to what you would see in humans, which is a nice bonus. I say “kind of” because it doesn’t really say how it works, it just shows you what it looks like. For the how it works bit, you need to think about some mathematics.

I also mentioned in the last chapter that the mathematics involved was kind of simple, for various reasons. This is so. The reasons are both personal and human. They have in the past got me into sort of trouble though. Once I was at a job interview where there was a talk required about the research the candidate does. I presented trust. It seemed like a good idea since that’s what I think about. All the time. I gave my talk, and was asked, pretty much right away, “Why do you say you use pseudo-maths for your formalization?” (or words to that effect). My answer was that I don’t really like maths. I don’t think it went down too well. I certainly didn’t get the job.

But the point is a good one. Too often we build more and more complex answers for computational systems to be able to handle the minutiae of complex human existence. Trust models are no exception, and this is not the right way to go. Why? This brings me to the second reason.

I don’t really hate maths. I just think it doesn’t have to be hard.

The models we build for trust and reputation have become so complex, in order to handle attacks or different circumstances, or whatever, that they are indecipherable by someone who doesn’t have a PhD in maths. This may seem like an exaggeration but consider: if the maths is too difficult for the people for whom the model is supposed to be working, what use is it?

This is a contentious way to start a book chapter, and the obvious retort is “well self-driving cars…” or “well space travel…” or whatever. No arguments from me that these things are complicated and people kind of expect that. I don’t for one second pretend to understand the maths involved in getting Armstrong, Collins and Aldrin to the moon, although as a very small less than one year old I did apparently watch. I don’t pretend to understand the systems of a self-driving car either. This is fine. In fact, when you think about it, it makes a lot of sense. These things are hard. Not only that, they take skill to even do without the computer, if that was even possible for Apollo 11. Driving a car is a complex task with plenty of responsibility involved; it’s not simple even for people. That’s why we have a driving test.

A drawing of a man and robot shaking hands symbolising trust between computers and humans. — Figure 5.1: People and Computers can Trust Each Other

However, trust is something we do. Every day. We are actually pretty good at it. Sometimes we get taken for a ride (about which, see the end of this chapter) but we really are pretty good at it. So why should the systems that are helping us to make trusting decisions be complicated black boxes that we need an advanced degree in maths to understand? Hint: it’s not because we don’t know how trust works. Ask a baby.

There are many many models of trust out there. Some of them are less complex, others are more so. It’s actually quite hard to keep track of all the models that keep appearing. There’s a reason though, that there are so many. It goes like this: there are many different uses you can put trust to — you can use it to decide on that infamous babysitter, you can use it to consider car mechanics, banks, politicians, who to buy from online, whether to follow advice (from online or not). Almost anywhere you have a decision to make where risk is involved you will see trust pop up. It isn’t always the primary tool being used, but it’ll be there. As we’ll see, sometimes it’s there considering something that seems completely orthogonal to the thing actually being considered.

Human beings are liminal creatures. We live on the edges of things – and if we are not on the edge we are heading there. Apart from the ubiquitous opposable thumb, one of the reasons why we are so successful at filling the ecosystems we are presented with is that we’re so adaptable and innovative. Whatever your thoughts about what humans are doing to the planet, this is hard to deny. Trust is representative of that: it’s a completely adaptable phenomenon that we use to help us in lots of ways. But we’re good at this stuff. Computers, not so much. Adaptation isn’t something that was considered a lot for a long time, and even now computers are a poor relation to the natural world. So, to make a trust model that works in a specific instance means that you need to create a specific trust model. That’s a thing.

A computer having problems ("out of cheese error"). — Figure 5.3: Sometimes computers don’t know the answer. (Thanks Sir Terry.)

As a result, generic trust models are few and far between. That there are any at all is testament to the belief that it should be possible and the tenacity of various researchers. Still, the general models aren’t brilliant. In the case of the one I created back in the early 1990s, it had less to do with tenacity and more to do with the fact that at the time I didn’t actually know you couldn’t.

The model itself is pretty simple mathematics-wise, but it is the first one that tried to bring together the computational and the social, the birth of computational trust. It is also quite generic, but one of its graces is that you can plug just about any inputs into it to make it more specialized. We’ll get to that. In this chapter I’m going to describe it for a couple of reasons. The most obvious is that it is mine, but on other levels, it is both simple and descriptive.

I recently came to the realization (as in, I was told) that I am a functionalist when things like this are concerned: it is less important to me the way something works than the fact that it does. More, that it does something that we might consider, functionally, to be what you are expecting. It’s easy to get into philosophical discussions about whether or not the systems using this (or other) trust model are actually thinking in trust, as it were, and somewhere in this book we might, but the fact is that they sometimes behave as if they are, and that’s enough for right now. We’ll come back to this, don’t worry.

Basic Trust

In the last chapter we used the continuum as a way of looking at how trust might look – sort of the way it might behave in different circumstances. Let’s flesh that out. In this model, there are three different kinds of trust and two questions. We’ve actually come across the two questions already in the previous chapter. That whole cooperation threshold thing revolves around them. The first is how much trust do you have (in a situation – remember trust is contextual) and the second is how much trust do you need in that situation. The second one is the cooperation threshold. I’ll show you how we calculate that shortly.

The first question requires us to look at our three different types of trust. We’ll do this from the point of view of the truster, which for the sake of simplicity we’ll call $x$ (you can call them Bob or Alice or whatever, it’s all good).

Our first kind of trust is the one that stays with us from pretty much when we’re born, if not before. It’s basic, learned from the environment and all our interactions, as well as our predispositions for whatever reason. We call it basic trust and, from the point of view of $x$ , we can represent it like this : $T_{x}$ . Figure 5.4 shows our stick person with that Basic Trust.

A stick person with a basic trust notation. — Figure 5.4: A Basic Trust Stick Person

It’s important, don’t forget it. Everything that happens to our wee truster, every experience, every interaction, everything, has an impact on this basic trust. As you might expect, at the start of the truster’s existence it might be quite volatile, but the more interactions they have, the less volatile it gets — it takes quite a lot to change the trusting nature of someone. Either quite a lot or something quite memorable.

So, that’s our basic trust. It doesn’t really help too much when little $x$ is thinking about another being in their existence. Let’s, for the sake of argument, call this new thing $y$ , shall we?

General Trust

In this instance, when we say that x is thinking about how much they ‘trust’ $y$ in general, we really mean is, based on the evidence, the interactions, history and so on that the two have together, $x$ thinks that $y$ is, for example, pretty trustworthy, or untrustworthy, or whatever. We call this general trust and we represent it like this: $T_x(y)$ .

This is important too. Remember it, there may be a quiz later.

Okay, so if people asked me if I trusted my brother^[1], with no context, I’d say, “Yes”. My general trust in him is pretty high. Trouble is, I am pretty sure his flying skills are at least as good as mine, which is to say non-existent. So, as I talked about in the previous chapter, in the context of flying the plane I was sitting in, I think my level of trust is basically in the “for goodness sake, no!” range that you can see in Figure 5.5 (Sorry, Pete).

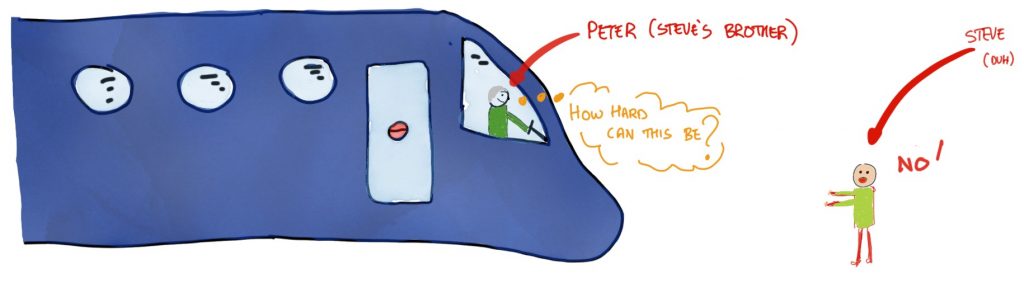
A plane with Steve's brother flying it, and Steve refusing to be part of that! — Figure 5.5: Peter wants to fly a plane. Steve isn’t so sure…

Situational Trust

What is missing then? I trust him a lot. I just don’t trust him to fly a plane (or perhaps to do brain surgery). The missing piece, of course, is context. Remember the trust system: people, process and place? Well, context is part of the place bit. In the formalization I created I eschewed the word ‘context’ for reasons I cannot fathom this far distant from the decision, and instead used the word ‘situation’. So what we have is what I called situational trust. It kind of stuck. This is represented for our little $x$ and $y$ as: $T_x(y,\alpha)$ .

Hang on! Hold those horses! See that new thing, $\alpha$ ? That’s the context or situation that the consideration is being done in. For example, it could be, “Do I trust my brother to fly the plane?” or, “Does Patricia trust me to cook saag paneer properly?” Which is wonderfully illustrated in Figure 5.6, if I say so myself.

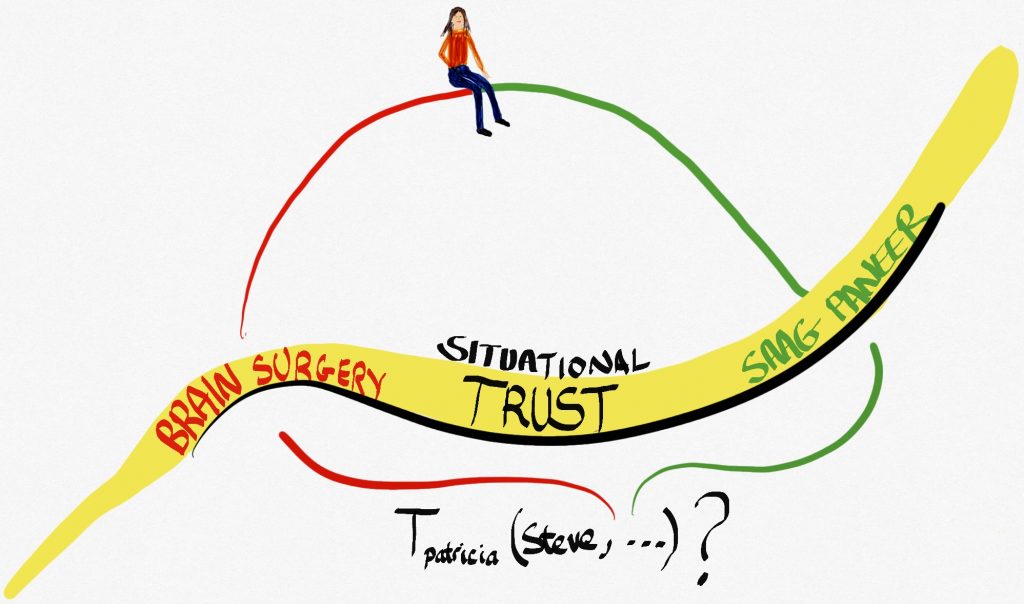
Patricia sitting on a continuum of trust from brain surgery to cookery. — Figure 5.6: Patricia and the “brain surgery vs. saag paneer cooking” conundrum

Situation, or context, can be anything that the truster is thinking about. Writing a letter, posting one, lending or borrowing money, driving, flying, hitting, you name it. As you might expect, it is also changing from instant to instant, because trust is not just contextual, it is contextual. Would I trust my brother to fly the plane if everyone else was incapacitated and he was the only one left? You tell me. Figure 5.7 might help…

Peter flying a plane on fire, the only person left... — Figure 5.7: Pete is the only one left to fly the plane or we all perish…

You see, context matters. But how do we plug all that context into the situation? Let’s see. But first, how did we get the general trust thing again? I mean, how does $x$ figure out how to trust $y$ in general if they’ve not met before?

It’s like this: in the absence of any other information, the value of at the start of a relationship is set to the basic trust $T_x$ . This solves lots of problems and seems to work pretty well — after all, it’s kind of how we work. The key words in the last but one sentence are “absence of any other information” because in general for someone you are entering into some kind of relationship with, there will probably be other cues, like referrals from friends or colleagues, reputation from the wider world, and so on — this is something Erving Goffmann pointed out in 1959:

“When an individual enters the presence of others, they commonly seek to acquire information about him or bring into play information about him already possessed … Information about the individual helps to define the situation, enabling others to know in advance what he will expect of them and what they may expect of him.”

(Goffman, 1959, page 13).

Still, it’s nice to know we can fall back on something, eh? Back to situational trust. It goes like this. Situational trust is calculated from three distinct functions, each of which is ultimately tailorable to match the kind of trust we want to model (like buying, selling, teaching, romantic relationships and so on – they all have different inputs to trust, right?). The equation looks like this:

$T_{x}(y,\alpha) = U_{x}(\alpha) \times I_{x}(\alpha) \times \widehat{T_x(y)}$

Utility

There’s a lot to unpack here, so let’s get to it.

You already know the left hand side, that’s easy. That’s just the situational trust, which will become a value (in a range $[-1,+1)$ – bear with me, we’ll get to those brackets).

The $U_{x}(\alpha)$ represents utility. Utility is a pretty loaded term when we talk in these kinds of contexts because it has specific meanings, like “what $x$ stands to get from something”. It could be counted as money or some other kinds of reward, like for instance the pleasure of a quiet night at the movies with your significant other while the baby is being looked after by the babysitter.

I can almost feel you thinking about the costs bit. Sure, yes, utility can be a cost-benefit analysis. You gain something but it costs you something. You pay the babysitter money. You have to work for your money, and so on. All very good, and you can plug these considerations in here.

(If you are now thinking “but the babysitter could…” then wait for a short while. We will get there.)

The thing about utility here is that you can pretty much plug in anything you want from what can be gained, and what it costs. If you’re buying, selling, working and so on it’s fairly clear. If you are thinking about the babysitter and the night out, that’s pretty straightforward too. It gets a bit more cloudy when you think about having your car maintenance done, especially if you’re short on cash — maybe it can wait a wee while, maybe the maintenance doesn’t feel like it’s giving you much right now (but wait until 3am on the highway…).

Steve in front of a broken down car, which he should have had the oil changed in a while ago. — Figure 5.8: Serves you right, Steve.

I think you get the point.

Another thing: in Game Theory, the people or agents being considered are expected to be rational utility maximizers, which is to say that they will choose the thing that they get the most reward from. This isn’t necessarily the case in this model.

Our second thing? $I_x(\alpha)$ is the importance of the situation for our little $x$ . You might think “well surely that’s the same thing as the utility,” but it isn’t, here. Importance is a measure of how much little x wants the thing to happen. Think about the babysitting thing for a moment: what if $x$ is in the military and tomorrow has to head out for a six month mission? How important is a few hours of time alone with their Significant Other compared to, say, a couple who go to the movies every week? It works for money too, although there’s a fuzzy ‘utility-lite’ thing happening here. How much more important is winning $10,000 to someone who has nothing in the bank than it is to your everyday billionaire? There is a utility thing here but I like to separate them because it makes more sense to me. I think of it like this: The utility of $10,000 is $10,000, if we are thinking money value only. But that doesn’t say much about how it might just change the life of the badly off compared to the billionaire (I know it would help me. I expect Jeff Bezos wouldn’t even notice it).

Jeff Bezos counting money - the utility of loads of money to Jeff is interesting - an extra $100 is of little utility but is of the same value as $100 for a poor person. — Figure 5.9: There’s a lot of money there, but what is the utility of all that money? Kind of depends on who is asking.

As with the utility, you can plug in any kind of consideration into importance. Probably you can be even more wild and wacky with what you plug in — things that matter are wildly different for different people, let alone in whatever different contexts there are. For instance, one of my horses right now needs his hooves trimmed. He’s actually a pony and I couldn’t ride him if I wanted (I suspect my feet would touch the ground!). The utility of having the hooves trimmed is pretty low (to me!). More trimmed hooves, a few hoof clippings for the dogs to play with. The importance is pretty high, because if not done then he is probably pretty uncomfortable. I’m sure the discomfort and subsequent lack thereof are actually of some utility to the pony because, hey, discomfort isn’t fun. It’s also probably of high importance to him, but of course I have no way of knowing.

Here’s the thing: I have no idea of knowing for you either (not for having your hooves trimmed, but I think you get the idea). Things like Importance and to a lesser degree utility are personal. That doesn’t mean we can’t guess (guesstimate?!) them though, and improve our guesses with observation and so on. That’s kind of what trust is like.

For the sake of completeness, when I was thinking about these two things I kind of assumed that they would be in the range of $(0,+1)$ . So there’s no negative utility or importance, for instance. If there was, I’m going to say that our little $x$ wouldn’t touch the situation with a bargepole. However, one of the more interesting things about the formalization is that it allows us to think things like “what if the utility was negative but the situation was really important?” – I’ll leave that as an exercise, both in terms of thinking up such an example and what it might mean.

The last thing in our situational trust equation is obviously expecting rain, for it has a hat: $\widehat{T_x(y)}$ . Clearly there is some magic at work here.

Okay, not really.

The hat is there to show us that we’re using some form of estimate or even calculation for what is really the general trust in $y$ of $x$ . What do I mean by that? Well, a lot of it has to do with what kind of person $x$ is. Pessimist? Optimist? Forgetful? Spiteful? You name it.

For instance, we might say that $x$ is a pretty rational agent, happy to think about all the experiences they have had with $y$ and basically average them all out, sort of a ‘fair comparison’ type of thing. In that case, you could say that:

$\widehat{T_x(y)}$ = $\frac{1}{|A|} \sum_{\alpha \in A}{T_x(y,\alpha)}$

Which is basically saying x will take the average of the results of (what happened in) all the experiences they have had with y in similar situations. Or you might say:

$\widehat{T_x(y)}$ = $\frac{1}{|n|} \sum_{t=1 .. 1-n}T_x(y)^t$

Which basically says, go back in memory for $n$ experiences regardless of whether they are similar or not and average that lot out. We introduce time here (that $t$ ) — hope that’s okay. Hard to talk about memory without bringing time into it.

You can play with this a lot. $x$ might consider memory and similar experiences. They might consider only positive experiences or just negative ones. Those last two are indicative of optimism or pessimism, by the way. What would an optimistic $x$ think? How about:

$\widehat{T_x(y)}$ = ${\rm max}(T_x(y,\alpha)^{t-1}, \ldots, T_x(y,\alpha)^{t-n})$

The thing is, as you may have spotted, it’s quite customizable to different kinds of people, agents, circumstances and so on.

It’s pretty neat.

Cooperation Threshold

Okay, that’s our first question (you remember: How much do I have?). The second one is how much trust do I need? This is also, as you might expect, quite tailorable, and it definitely tries to take into account some of the things I’ve taken about in the previous chapters. Let’s just right into it. As you already know; it’s called the cooperation threshold. Here’s how I calculate it:

${\rm Cooperation\_Threshold}_x(y,\alpha) = \frac{{\rm Perceived\_Risk}_x(\alpha)}{{\rm Perceived\_Competence}_x(y,\alpha)} \times I_x(\alpha)$

Woot, that’s pretty interesting! (I would say that.)

Okay, so let’s see. We’ll start with the fact that a negative cooperation threshold simply doesn’t make sense — well, if it was negative we’d cooperate with those we distrust, even. There may well be some examples in international espionage or the old Great Game where this is the case, but let’s leave the Machiavellian stuff out for now. So this is going to have a value in the range $(0,+1)$ . We’ll normalize it if we have to, which is to say, if the answer comes out to more than one we’ll just make it one, and make it zero for less than zero. Yes, I know that the negative ones are interesting, and indeed the greater than one situation tells us we’d never cooperate, but in the first instance we’re ignoring the issue and in the second, since Situational Trust can never be +1, it’s a moot point.

Perceived Risk

So ${\rm Perceived\_Risk}_x(\alpha)$ . is pretty straightforward. How risky is the situation? There are plenty of different risk estimation things out there so I won’t go into that here. Risk estimation in general is something humans are pretty rubbish at though, which is at least a point for the computational side!

A robot holding its hands up in the air and shouting "woohoo! something I am good at!" — Figure 5.9: In risk estimation, the agent finally feels valued.

Remember that whole regret and forgiveness thing we got to in the last chapter? If you recall, they were really interesting tools for helping figure out how trust goes up and down in different circumstances. This is indeed true, but I didn’t really talk about what that really meant. In other words, how does it work?

Like most things to do with the model I’m presenting here, the answer is “that’s up to you” but the general idea comes from Jonker et al (2004) who in a nutshell found that positive experiences increases trust and negative ones decrease it. You probably are thinking “yep, figured that out for myself” but firstly it never hurts to check and secondly they also found out other things. Like for instance that positive (say maximum) trust was reached after two positive experiences and negative after three (or two, depending) negative experiences. Now, take that with whatever amount of salt you wish. The thing is, we can all pretty much agree that trust does go up and down. I showed you a bunch of pretty graphs with absolutely no scales on them (oops) in the previous chapter, so there we are, that proves it.

But how much?

That’s the real question, isn’t it? If you get into a relationship and things go Pete Tong (look it up, I can’t do all the work for you), how much trust do you lose? How much do you gain if things keep going well? Recall from the last chapter that trust is often seen as fragile (slow up, quick down) and there may be plateaus around there someplace.

For this, there are many different formulae, all of them sensible. Cast your mind back to the chapter on Prisoners. Remember tit-for-tat? You could say that its trust went to maximum after a positive experience and minimum after a negative one. You could also say it was very forgiving, so if its opponent went back to being nice, then after one round it was forgiven. Extreme? Maybe. Works? Sure. As you can imagine, it gets more complex from there. In the model I’m showing you in this chapter, we did it in a few different ways. There are reasons for this, much of them have to do with the fact that if you remember we were interested to see how trust worked and so playing around with different behaviours made sense.

Anyway, at its simplest we said that you could increase trust by some value related to how important the situation was after a positive experience, and decrease it similarly if the experience had been negative. That might look something like this:

$T_x(y)^{t+1} = T_x(y)^t \pm f(I_x(\alpha)^t)$

This has the merit of being simple but has the fault of showing us pretty much not much. What is this function and how does it work? As ever, it’s up to you. For instance, it could look like:

$f(I_x(\alpha)^t) = \frac{I_x(\alpha)^t}{10}$

Which means that the trust will go up or down by one tenth of the importance of the situation to $x$ . Doesn’t take into account fragility though, so you can figure out that it would probably make sense to say something like “after a negative experience reduce trust by ten times importance, after a positive one, increase it by one tenth of importance”. That would do the trick. The result is that trust increases ten times slower than it decreases. Again, this is easy to play with and there are so many different things that can influence it, For example, optimism, pessimism and (ta da!) regret or forgiveness.

Regret

So, if you recall, regret was a couple of things. The first was as a decision tool. In this instance, we use it to say things like “I will regret this if I don’t do it” or “I am going to regret this”. You get the idea. In that mode, you could plug anticipatory regret into the formula for the cooperation threshold above. What might that look like? For the sake of argument let’s say that we can calculate anticipatory regret, so we don’t have to work that in here. How might we do that? Well, to be sure it’s really just a guess in any case, but in a world with perfect information you might be able to do things with utility offing something versus not doing it at all. This isn’t the same as doing it and it not happening though. For instance, if I don’t buy a lottery ticket one week and my numbers come up, there’s quite a bit of difference between not buying one and not having a set of favourite numbers in the first place, or buying one and having the numbers not come up. There’s some great research on that too, which right at the end of the book you’ll find pointers to.

Anyway, assuming we guessed how much we would regret not doing something it might look like this:

${\rm Cooperation\_Threshold}_x(y,\alpha) =$

$\frac{{\rm Perceived\_Risk}_x(\alpha)}{{\rm Perceived\_Competence}_x(y,\alpha)} \times I_x(\alpha) - {\rm Regret}_x(\neg \alpha)$

In case you’re not familiar with the notation, that strange $neg$ in the Regret thing means “not”. So, as you can see here, this has the effect of lowering the cooperation threshold by how much $x$ thinks they are going to regret not doing this thing (and so increases the likelihood they will do it, as it were). You can do similar things with “regret it if I do it” and so on.

On the other side of the behaviours comes “what happens after bad things got done”. In other words, how much does $x$ regret having trusted $y$ because $y$ betrayed $x$ ?

As with most things, this kind of depends. It depends on how much $x$ does regret trusting $y$ . It may well also depend on how much regret $y$ feels that they betrayed $x$ . Because it may have been an accident. It may have been a stupid slip. Or it could be quite purposeful and no regret felt. As with most things in this little convoluted world of trust, even an expression of regret may be insincere. Regardless, we do have some thoughts on it.

The first is to think about how much $x$ regrets the betrayal. This is kind of related to how much they regret trusting $y$ in the first place, and how much they lost from the betrayal — these two things are not the same, as a moment’s thought will show you. For the sake of simplicity here, we use one formula that brings both of these things together:

${\rm Regret}_x(\alpha) = (U_x(\alpha) - U_x(\alpha')) \bullet f(\kappa, \lambda, \mu)$

This takes some unpacking, so let’s start. Here, $U_x(\alpha)$ is what $x$ actually expected from the situation (if it had all worked out) and $U_x(\alpha')$ is what $x$ actually got (which might be nothing, or worse. Note that if it’s negative, then it actually cost $x$ something, which does bad things to regret!).

Okay, but what about that function: $f(\kappa,\ lambda, \mu)$ ? Well, this tries to take into account some of the more emotional aspects of the situation. Some of these variables are relatively straightforward for our computational friends, others not so much. That’s life. Here we go.

First, kappa (that’s the one that looks like a $\kappa$ – have you ever wondered why we use Greek letters in this kind of thing? I mean, like $\alpha, \beta$ and stuff like that? There are a few conventions. I’ve broken a few of these rules in my own equations because the letters are supposed to mean something specific in a lot of cases, but hey, I think I’ll survive).

Anyway, kappa ( $\kappa$ )stands in this formula for what was lost. You could look at this in purely utilitarian terms (which is easy for the rational stuff) but there is a reason it is there. The loss of something like a relationship, or innocence, or whatever, is a visceral thing. That kind of loss fits here too.

The next Greek letter is lambda ( $\lambda$ – and definitely this is conventionally to do with things like wavelengths in physics and so on, but here, not so much!). In this instance, lambda ( $\lambda$ ) stands for “what it meant” to the agent. Again, this is a bit hard to pin down, but it has to do with things like the importance of the thing that was expected. Sometimes, really small things have a very large importance, they “mean” something to us. That fits here.

And finally, we have mu. Yes, mu. This looks like $\mu$ (and yet another convention is crushed – serious mathematicians would say mu like that was for an Average! Which begs a question as to why they wouldn’t just say “Average”. There are probably lots of reasons for this but certainly one of them is that, well, we all like to feel special).

In this formula, mu ( $\mu$ ) stands for “how it felt”. Now this one is really hard to pin down for a computer. However, if you think about it as a human, being betrayed, losing something important, things like that, that feels bad. That’s what we are trying to capture here.

So we have… what was lost, what it meant, and how it felt. I think you’ll agree that these things pretty much sum up the pain of regret in a lot of ways.

And yes, we can of course plug in various ways of calculating it. For instance (pay attention, this one has something new in it…), let’s say that $x$ actually already knows $y$ . In this instance, by ‘knows’ we mean ‘has had experiences involving…’ which basically means that there is some form of relationship there.

The word relationship conjures up a lot of different things. For instance, it might be just a “oh sure, I know that person, we’ve talked a couple of times” all the way to “life without them would be like a broken pencil”, with of course many points between. The reason that this is important is that it says something about the meaning of the relationship to (in this case) $x$ . And as we’ve seen above, meaning is something important in our function. So let’s say that the importance of the relationship has an impact here.

So far so good.

Now, the situation where $x$ has trusted $y$ also means something. In the formulae that we have seen so far, this is best represented by how we calculate the cooperation threshold: there’s competence, there’s risk and there’s importance. We also started thinking about that regret part too (either “I will regret it if I do it” or “I will regret it if I don’t”, sort of thing).

Ultimately, what the cooperation threshold becomes is a signal of how much the agent wants to get this ‘thing’ done in this context. It also wraps into it things like how important it is to the agent that the job is done properly.

There are a couple of asides here. Those two things don’t always play well together. I mean, you might want something done really badly and want it done properly, but the “want it done really badly” might also mean that you are prepared to accept a less than perfect job so that it does get done.

I’m sure you can see the problems with all this. Humans are quite complex beasts and to be honest trust and things like that are not the only motivators that we have. The computational systems this model aims to help are no less complex, but they do have the benefit of being to some extent under our control. This means we can choose what we think makes sense.

For the sake of argument in this instance, let’s say that what makes sense is that the higher the cooperation threshold the more the important job is. The lower the cooperation threshold the less important it is (because our agent is happy to accept a shoddy job). This means that, the higher the cooperation threshold the more likely it is that things like “what was lost” and “what it meant” are badly affected. Okay, so that would mean we could say that our function looks something like this:

$f(\lambda, \kappa, \mu) = {\rm Cooperation\_Threshold}_x(y, \alpha) + I_x(xy)$

Smashing, now we are cooking with non-renewable hydrocarbons.

See that last thing? It says $I_x(xy)$ . In our notation, this means the importance of the relationship to $x$ . It’s similar to the importance of a situation in its makeup, but it says more about the inter-personal (inter-agent) relationship.

One last thing before we go to the next bit. You may have noticed that none of $\lambda$ , $\kappa$ or indeed $\mu$ appear in the calculations we make. This makes it not so much a function as a way of thinking about the situation for $x$ . As I’ve said many times, trust is personal and the things that matter are likewise personal. In this instance, those three Greek letters are placeholders for anyone looking at the formula to realize what it is really trying to say: that regret is multi-faceted and should take into account much more than an opportunity cost. As such, it may be that you can think of a different formula to put in there, and that would be just fine. Better in fact, in some ways, than copying what is there, because it is yours. The beauty of all of this is its customizability: this is not a set of formulae that say “this is how trust works”, it is the start of a conversation about how trust might look. Perhaps most of all it is a framework that people can use to make trust-reasoning computational agents that think like they do. And that is worth a lot of complicated equations.

One last example. Perhaps $x$ and $y$ don’t know each other, it’s a first interaction. We can get really simple here and say something like:

$f(\lambda, \kappa, \mu) = I_x(\alpha)$

Which kind of makes sense because all $x$ really wants to think about is how important it was that this thing got done (and what it felt like when it didn’t).

Think you can find different ways of thinking about it? Awesome. You have my blessings.

Now, we’ve arrived at a way to think about how much trust goes up and down. One that takes into account regret, that is. Which was one of the things that we were trying to figure out at the start! It’s a long journey, sorry. You may recall, if you’re still with me, that we had a pretty simple equation before, like this:

$T_x(y)^{t+1} = T_x(y)^t \pm f(I_x(\alpha)^t)$

And we talked about what that function of importance might look like, and so on. Now we can bring in regret, which is cool. Why is it cool? Because it allows us to further enhance the way the model can work.

We now have a way of calculating regret. If you remember, it looked like this:

${\rm Regret}_x(\alpha) = (U_x(\alpha) - U_x(\alpha')) \bullet f(\kappa, \lambda, \mu)$

So how does this sound: The more x regrets that the situation went bad, the more trust that they are likely to lose in y. Yes, there are plenty of other ways to think about it, that’s the entire point and beauty of the whole thing! But we’ll stick with that for now. So, we can now come to a different equation for adjusting trust. This can work in both “that went well” and “that was pretty bad, why did they do that?” situations, and more…

$T_x(y)^{t+1} = T_x(y)^t \pm f(\alpha, {\rm Cooperation\_Threshold}_x(y, \alpha), T_x(y, \alpha), {\rm Regret}_x(\alpha), {\rm Regret}_y((\alpha))$

That’s a bit big, but if you read it carefully you will see that all it is saying is that the amount of decline or increase in trust that $x$ has in $y$ is dependent on:

The situation itself (which gives us context);
The cooperation threshold for the situation (which if you remember was a sign of things like how the situation mattered to $x$ , but in this instance also could be used for things like “it should have been done well” and so on);
The trust that 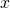$x$ had in 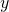$y$ for that situation (remember that this takes into account a bunch of things like importance and utility);
The regret (if any) that 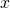$x$ feels about how the situation went (this could be none at all if it went really well, don’t forget); and
The regret (if any) that 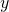$y$ feels about how the situation went (again, this could be none at all if it went really well, but it could be nothing at all if 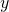$y$ betrayed 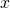$x$ and doesn’t care).

Now, does it make sense? And can you see how all of it ties together to make the model work in situations where good and/or bad things happen? I hope so! If it helps, it took me nearly 30 years to get to this stage, and there’s a lot of research behind it, which you can find in the last bit of the book. For the sake of completeness, we suggested in Marsh and Briggs (2015) that it might look a bit like this:

$f =\frac{{\rm Cooperation\_Threshold}_x(y, \alpha) + T_x(y, \alpha)^t}{\Xi_x} \times ({\rm Regret}_x(\alpha) - {\rm Regret}_y(\alpha))$

That is probably self-explanatory except for one thing, that interesting little $\Xi$ . Firstly, it’s the Greek letter Xi, which is pretty neat. Secondly, it is definitely something that $x$ is ‘thinking’ about (because of the little $x$ that is there. The most important bit is what it means, which is: how understanding $x$ is about the whole thing. The more understanding they are, the less effect the whole thing will have on the trust reduction after a betrayal. It is a number and you get to pick it to dictate how understanding your agent is. Yet another way to personalize the agent…

One last thing that we need to get to is that whole thing about forgiveness. As a matter of fact it’s a little bit related to that understanding bit, in the sense that it introduces another kind of ‘trait’ for the agent that explains why some things happen the way they do.

Think back to the last chapter. We looked at forgiveness as a way of rebuilding trust after bad things happened, and we even had nice graphs and that. I also talked about the work Pitt and others had done in the area where forgiveness in online people was concerned (it takes a while, needs apologies, that kind of thing).

Well, consider yourself fortunate because now we get to use our regret things again! We also get to think about what forgiveness might actually look like to a computational agent.

First things first. We are going to assume that:

Forgiveness may not happen at all;
If forgiveness does happen, it will be after some time that is dependent on the severity of the betrayal; and
If and when forgiveness does happen, trust can be rebuilt at a speed that is dependent on the severity of the betrayal.

These are my assumptions. You can make your own if you wish. For example, you might change number 3 to say something like “if and when forgiveness happens it retires trust to its prior level” (which is pretty much what Vasalou et all did post apology in their work). There are lots of ways. You choose. Sound familiar? (It is a bit like a choose your own adventure, I agree.)

By the way, assumptions are a key part of things like this, if not much of science. The first thing we do is say what we believe to be the foundational bit – the things that need to be true for us to be able to carry on with the rest. Sometimes that means we remove some aspect of things like behaviour that we are worried will make things complicated, sometimes we make assumptions like “humans are rational actors”. It helps to clear the path forward. It also allows others to come and say “well, that assumption is a bit rubbish, what happens if you get rid of it or change it?” To which you can say “I don’t know, figure it our for yourself.” And that.

Given those three assumptions then, here’s what we can do with forgiveness. The first thing is say “well, it’s going to take a while” and this looks like:

$T_x(y)^{t+Ft_x} = T_x(y)^t + Fk_x$

Let me explain. Firstly on the left hand side we see $T_x(y)^{t+Ft_x}$ , which means that the General Trust of $x$ in $y$ after a time equal to now (that’s the $t$ ) plus $Ft_x$ something will happen (which we will get to). That is what we decided to call the forgiveness trait of (in this instance) $x$ . Remember I told you there was another trait thing going to happen? Here it is. What this means is that there is a sort of “how forgiving” measure for the agent. If you think about it, there’s probably one for you too. If you think about it a bit further, you might realize that it depends on who you might be thinking about and what for and so on, and you will see that this one here is a little too simple to map out humans.

It is, but it’ll do for our model right now. I quoted Lieutenant Commander Data in the previous chapter talking about 0.68 seconds. Ultimately, this will arrive at something like that: a length of time that makes sense in the circumstances to the agents involved.

One caveat to notice here: the higher this number is, the longer it takes to start forgiving. This means that the higher $Ft_x$ is the longer it will take to forgive, which means that it is a measure of how unforgiving the agent is. Bear that in mind.

Then on the right-hand side there’s: $T_x(y)^t + Fk_x$ . The first item is self explanatory: how much does $x$ trust $y$ right now?

Stop there a moment. Consider that something bad just happened. What have we already done? Yes, reduce the trust. So this $T_x(y)^t$ means the trust after we’ve taken into account what happened (it might be pretty low, to be honest). Also bear in mind item 1 in our list above: forgiveness might not happen at all. This might be because the agent just doesn’t feel like it, or the trust went below our limit of forgivability, things like that. We’ll come back to that. For now, assume that we will start the forgiveness process. So this leaves us with how. The $Fk_x$ gives us the answer. Remember point 3 in our list. The rate of increase depends on the severity of the betrayal. Bad means it’s going to take a long while, less bad means it might be quicker, and so on. In our equations we also mixed in a bit of regret (which is akin to the apology that Vasalou et al talk about). And so, we arrive here:

$Fk_x = \frac{({\rm Regret}_y(\alpha) - {\rm Regret}_x(\alpha) + I_x(xy))}{Ft_x} \times T_x(y)$

Which means that how quickly forgiveness happens depends on the apologies, regret, the importance of the relationship, how much trust there was in the first place (when the thing that was bad happened) and that good old forgiveness trait. Remember it was really how unforgiving $x$ was? That’s right: the less forgiving $x$ is, the lower this number is going to be, and the slower forgiveness will be.

One very last thing about this. I have talked about the limit of forgivability before but I haven’t really said how to figure it out. In the work we do here, the limit of forgivability is very closely related to that forgiveness trait. One way you could calculate it would be like this:

${\rm Limit\_of\_Forgivability}_x = -(1-Ft_x)$

Which if you look at it says “the higher that number is, the closer to 0 that limit of forgivability is” which is the same as saying that the higher the number is, the much less likely forgiveness will happen at all after a transgression.

That Pesky Zero, That Even Peskier +1!

Much of what is written here begs a question. We can calculate all kinds of things about trust and distrust, forgiveness and so on, but there’s this very special value in the middle which is complicating things. What exactly does 0 (zero) mean in this model? It isn’t trust and it isn’t distrust. It could represent the fact that the truster has no information to make decisions. It could mean that the truster is ambivalent. It could mean, frankly, pretty much anything. I’ve glossed over it a little in the text above, but I wanted to point at it and say “this is something that you really need to think about.’ As it happens, I have. The concept of having a zero trust value is discussed in my PhD thesis (which is lucky). I decided that it could mean, well, whatever the context wanted it to mean – lack of information, a decision not yet made, a specific decision made that, for instance, refuses to consider anyone in a given situation as trusted or distrusted until they are asked (or they ask) to do something – this last one is basically what the concept of Zero Trust in security is about.

It’s basically your call. Isn’t freedom to choose grand?

Now I did say earlier that I would come back to those interesting brackets for [-1,+1). They basically mean that there is no +1 trust. “But,” I hear you say “of course there is, what if you trust someone completely?”

Let me explain. Belief in a deity, or some supreme being is what we’re talking about here. It has a name too: faith. It has another name – blind trust. What does this mean actually? It means that the truster has made a decision to trust completely regardless of any evidence, in fact. in the absence of any evidence one way or another. Trust is a consideration of risk in a situation (as you hopefully spotted) but in a situation of blind trust there is no consideration, there is just acceptance. This isn’t in line with how we (or others like Luhmann or Broadie or Dasgupta) think about trust. In fact, it simply isn’t trust at all, in the sense that consideration of the other is made. If you enter a relationship without considering the potential pitfalls, this doesn’t make you safer, it makes you credulous.

I’ve nothing against faith, demanded by a deity or simply freely given by someone to someone else, but it’s not trust. Do I trust my partner Patricia completely? Of course. But this is tempered by experience, time, behaviours and so on to become faith and belief. There are, in other words, situations where I don’t have to think about trusting her because I already know I don’t need to trust her – there’s no risk.

I imagine that kind of belief is true for people who have faith in their God.

Note carefully that this is not the same as control. As Cofta notes, trust and control are different, but they can result in similar outcomes as faith. That is, if I control completely something else, and there is complete transparency in this control situation, then I don’t need to think about trust then either because I know what I want to happen will happen. Is this another +1 situation? Well, no, because in the +1 situation you are putting yourself completely in the hands of ‘another.’ Whereas in the control situation you aren’t, you just know it will work because you are making it so.

Now this is all my opinion of course, based on observation and reading of other works. You may well disagree and that’s also okay. As an exercise, consider and try to describe a relationship where that +1 exists as trust.

On Other Models and Representations

You may have noticed that the model I presented in the this chapter was my own – that is, the one I have worked on for man-years. This is so, but as you may also have surmised, this is not the only trust model out there. In fact, there are hundreds, possibly even thousands, of them. Some are dedicated to eCommerce environments. Some are used in the context of information retrieval and search. Some are logical, some much more deeply advanced mathematically than that which I presented in this chapter. Many of them work toward attack resistance, whilst others try to more accurately model the ways in which humans consider trust-based decisions.

And all of them are valuable additions to a growing field.

Here’s the thing though: presenting them all in this chapter is impractical at best. There are so many, to start with. The fact that many of them are highly contextual (like trust) and applied in a narrow area of use is something slightly more problematic. There are general models of trust (like the one in this chapter) but they aren’t hugely popular because they don’t answer specific problems particularly elegantly. They are not really meant to, but like general purpose computers, they can almost certainly be ‘programmed’ to make them more contextually narrow.

One of the more interesting of the general purpose models is that of Christiano Castelfranchi and colleagues (Rino Falcone, Rosaria Conte and others). It’s interesting because it looks at trust from a psychological, cognitive point of view – none of the problems of values that you saw earlier in the chapter for this model. The model is goal-based (cognitive agents have goals) and has notions of CoreTrust, Delegation, plausibility and preferences in it that are very powerful and it has been implemented in a computational setting. Like the model in this chapter it also addresses things like Mistrust and Distrust. You can find out more about this model in Castelfranchi and Falcone’s excellent book, which certainly holds the mantle of being the first book covering computational trust as a theory. Despite its age (published in 2010) the principles and observations about trust in the book are as current as when the book was published.

Discussion of trust values and calculations would be incomplete without a short look at Audun Jøsang’s work. Jøsang created a subjective logic for trust that is based on three values – belief, disbelief and uncertainty, adapting Bayesian mathematics for opinion-based reasoning. He provides a set of operators for the model and shows how it can work in this excellent tutorial.

This actually brings us to the problem of how to represent trust. Jøsang does it using subjective logic’s tuple of values (which has the added nicety of being representable using a nice triangle of trust reasoning). My own looks at trust as a measure in the range of [-1,+1). Castelfranchi et al’s used cognitive models. Others use fuzzy logics or fuzzy notions (for instance PGP, which I talk about in another chapter). Some are simply binary (one trust or doesn’t). Does the representation matter? Sort of. Words, and values, have power. They push the way you think about something in particular directions. For example, if a trust model had representations of trust between 0 and 1 may lead you to thinking that the nuances of positive trust are much more important than those of distrust (if it would lead you to think of it at all). If the model suggests that trust is from 0.5 up and distrust (or whatever) is from 0.5 down, it’s equivalent to the [-1,+1) in some ways but it points you in the direction of thinking about trust and distrust as ultimately connected in ways that they aren’t (well, I don’t think so anyway, which is why, although there’s a continuum, there’s a really special spot in the middle at 0 which means, well, something special in different contexts (see for example Zero Trust in a later chapter).

The problem is: what does 0.5 mean? What does a matrix representing different tuples, or a diagram of a triangle or whatever really mean? We’re still in the infancy of understanding trust and modelling it, as this chapter may have said a few times, and to be honest, it’s even more complex when you start realizing that even within the same model, comparing values is less than an exact science. But then, as Christian Jensen says, perhaps all you really need is a way to measure your own values so that you can compare one option against another and make a sensible (more rational) decision. Sharing trust isn’t an exact science in humans either. Try it. Your “I trust them completely” may be my “I trust them a lot” – they’re simply not the same things for different people. This is in no way a shortcoming of trust, or the models of it. A long time ago I came up with the idea of Comfort, which is a way to abstract trust ‘values’ to allow people and technologies to share them. Comfort, I suggested, was much more understandable and shareable, so I did some modelling there too. But at the end of the day, emotions (which trust is) are personal, that’s the point.

Meanwhile, whilst are certainly some literature reviews out there that have looked at many trust, reputation, eCommerce and so on models, as far as I can tell, there haven’t really been many published in the recent past, which is something that is worth thinking about doing. Maybe it’s something you, dear reader, might want to attempt…

Final Words

This has been a bit of a marathon chapter but at the end we’ve (hopefully) come to a really strong understanding of how things might work with trust in a computational agent. As you have seen along the journey, there is an awful lot of “you figure out what to put there” here that essentially makes the end result extremely tailorable and therefore really able to match what you want it to look like.

One last note about that, then, because it matters. A problem with many ecosystems is similarity. The more similar things are, the easier they are to attack (which is why the pandemic we experienced in 2020-2021 was so serious – we’re all so very nearly the same and none of us could handle this new thing). Trust is like that. The more similar it is across people, the easier it is to attack. We have the potential in a computational system to make it work in lots of different ways, and to think about many different things that matter just to one agent. This makes it harder to figure out which bits to attack in the different agents. It’s a relatively simple defence mechanism, but I’ll take it.

Of course, one of the reasons people like conmen thrive abusing trust is that we, as people, are so embarrassed by the whole idea of being taken for a ride (“chump”, “sucker” and so on are not compliments). Why? Because as I said earlier in this tome, we think we’re good at this stuff. We think we’re experts. No expert wants someone to come up and say “you’re wrong, look at this squiggly bit here, it completely messes up your whole theory”. Oh, all of us scientists like to say “science is all about theories that can be disproved” and so on, but we’ll still fight like demons to defend those same theories when they start getting looked at closely. As in science, so in trust and the general population. Except that, when we get suckered, we clam up and don’t tell anyone, fighting that little battle inside our own heads over and over again. This is of course unhealthy but oh so very human.

What can we learn from this? Computational agents don’t have an ego to crush (at least I don’t think they do right now, and if they did we’d deal with it then). They don’t care about embarrassment. So they can speak out about when they get attacked, if they spot it. And the others around them can make adjustments, and censure the attacker. And so on. But there’s more to it than that. If you recall in the previous chapter I started getting a bit philosophical when I discussed wa, calculus-based, knowledge-based and identification-based trusts and so on. All of this has to do with reputation, recommendation, honesty, truth and more. And some of that we’ll look at in the next chapter. See you there!

who as I type this has just finished his own PhD! Yay Pete! ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License