Introduction

Some molecules of a liquid can escape from the liquid surface (evaporate) because of their kinetic energy.  If these molecules, now in the vapour phase, are collected in a closed container, they will exert a pressure that is known as the vapour pressure, P^*, of the liquid, as indicated in Figure 1.

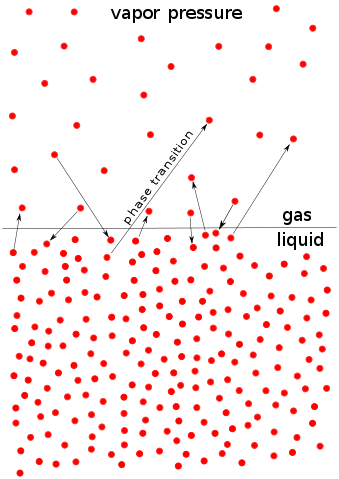
Figure 1: The microscopic process of evaporation and condensation at the liquid surface, by HellTchi, licensed under CC BY-SA 3.0

As the temperature increases so does the kinetic energy of molecules.  Then more molecules escape the liquid phase (evaporate) and the number of molecules above the liquid increases, yielding a higher vapour pressure.  Consequently, the vapour pressure of a liquid depends heavily on temperature.  The higher the temperature, the higher the vapour pressure.  The relationship is not linear, though, but follows the expression

(1)  

where T is the absolute temperature, and A, B are constants for any given liquid.

When the temperature is such that the vapour pressure of a liquid reaches the outside pressure (which is often atmospheric pressure), the liquid will start boiling.  When boiling happens, if additional energy is supplied, the temperature and pressure will remain constant until all the liquid evaporates, unless the system is in a closed container.  In a closed container, the generated vapours will increase the pressure and the liquid will stop boiling (because the container pressure will be higher than the vapour pressure), unless its temperature also increases.

To measure the vapour pressure of a liquid we exploit this principle that the liquid boils when its temperature is such that the vapour pressure is equal to the system pressure.  We set the pressure of the system and slowly heat-up the  liquid until it starts boiling.  If the process happens slow-enough, as it should be, it is difficult to visually assess when boiling happens (there will be no vigorous bubbling).  Therefore, we rely on temperature to assess boiling: boiling happens when the temperature of the liquid stays constant while being heated because all the added energy is used for phase change.

If we use this technique to calculate the vapour pressure at a few temperature levels, we can then employ equation (1) to calculate the vapour pressure at any temperature.  The easiest way to do this is by plotting log₁₀P versus 1/T which yields a straight line with intercept A and slope B.

The apparatus used in the E030 lab is a simple one consisting of parts that can be found in any chemistry lab.  The main parts of the apparatus are shown in Figure 2.  Essentially, a small flask is placed under low (vacuum) pressure using the lab’s vacuum line.  Methanol is added into this low-pressure space and is heated through a hot-water bath.  The methanol’s temperature is constantly monitored to assess when the methanol boils under the system’s pressure, which, as mentioned above, provides the boiling temperature at the system’s pressure or the vapour pressure at this temperature.  This process is continuously repeated at increasing pressures to provide a set of vapour pressures at different temperatures.

Figure 2: Vapour pressure apparatus in E030

Purpose

The purpose of the experiment is:

1. To understand what vapour pressure is and how it changes with temperature.
2. To understand the relationship between vapour pressure at a given temperature and boiling temperature at a given pressure.
3. To determine the vapour pressure of a pure liquid at various temperatures.

Procedure

Before proceeding, check your understanding by performing the following drag-and-drop task.

You are given a set of temperatures and vapour pressures for a substance.  The data sets are not ordered; so, you must match the temperature with the vapour pressure.  Recall that the relationship is monotonic: higher temperature leads to higher vapour pressure.

1. Ensure that the stopcock from the funnel is closed.  Place about 10 mL of methanol into the funnel of the vapour pressure apparatus. Set the water bath around the flask and start its stirring but do not heat yet.
2. Connect the apparatus to the vacuum tap and turn on the tap.  Evacuate the entire apparatus until the pressure inside is about 120 mmHg.  *NOTE: Make sure there are no leaks in the apparatus by observing the “vacuum pressure”; it should be constant.
3. Allow a small amount of liquid (enough so that there is visible liquid in the flask) from the funnel to run onto the cotton fibre around the thermometer bulb. Heat the water bath until the temperature is 5 to 10°C above the thermometer reading in the flask.  Heat the water slowly, as you do not want to overshoot the bath temperature.
4. Start recording (1) the temperature of the flask thermometer, (2) the temperature of the bath, and (3) the system pressure every 30 seconds. (three readings every 30 seconds for the duration of the experiment).
5. When the flask thermometer reading remains constant, the liquid on the cotton should be in equilibrium with its vapours at the pressure in the apparatus. This happens because all the energy transfer from the hotter bath to the methanol in the flask is used for evaporating the methanol (i.e. methanol boils at the apparatus pressure), which occurs at constant temperature.  Take a special note of this flask temperature and the corresponding pressure.  This constitutes a pair of vapour pressure at that temperature (or boiling point at that pressure).
6. Increase the pressure into the apparatus by about 50 mmHg. This can happen by tightening the clamp on the hose leading to the vacuum tap.  Increasing the pressure will increase the boiling temperature of methanol.  Then, the temperature of the flask will start increasing as the methanol gets heated by the hotter bath (ensure that the hot bath is always 5-10°C hotter than the flask).  This temperature increase will stop when the boiling point of methanol at the new pressure is reached.  Take a special note of this flask temperature and the corresponding pressure.  This constitutes a new pair of vapour pressure at that temperature (or boiling point at that pressure).
7. Repeat the above procedure several times until atmospheric pressure of approximately 760 mmHg is reached.
8. When the experiment is finished, allow air into the apparatus until the pressure inside and outside are equalized. Disassemble the system and remove the cotton fibre.  Clean and dry the flask and put cold water back into the water bath.
9. Repeat the experiment.

Report

First we will look at the raw data collected during the experiment

1. Provide two Tables, one for each run, with your recordings of time, flask temperature, hot bath temperature, and system pressure.
2. Plot the data of these two Tables.  One graph for each run.  Place time on the x-axis.  The graph must have three sets of data/lines.  The two temperatures must be on one y-axis and pressure on another axis.
3. Use the Tables created in step 1 above, the plots created in step 2, or your notes from the experiment (during step 5 and 6 of the procedure) to identify pairs of vapour pressure and corresponding temperature.  Provide these pairs in Two Tables, one for each run. (the Tables can be combined into one, as long as the labeling is clear).
   
   
4. Plot on one graph the vapour pressure and temperature pairs for each run.  The Table must have two sets of data, one for each run, with temperature on the x-axis.
5. Get a literature value for the “Normal Boiling Point” (NBP) of methanol (clearly state your source) and add it to the graph created in step 4.
6. Comment on the graph created on steps 4 and 5:
   1. What is the relationship between vapour pressure and temperature?
   2. Are there differences between the two runs?  What are any causes of such differences?
   3. How well do your experimental measurements compare to the NBP of methanol? Why are there differences, if any?
7. Now we can manipulate the data to make predictions.  As mentioned in the introduction, the relationship between vapour pressure and temperature follows the expression:

   (2)  

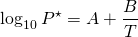
   We want to calculate the parameters A and B in order to be able to predict the vapour pressure of methanol and any temperature.
   For this task you should use the data collected during both runs.  Combine the vapour pressure – temperature data from both runs into one Table.  If your plot created during step 4 above clearly indicates that the data from one of the two runs is flawed, use data from only one run but clearly state that you are doing this.

   1. Tabulate: temperature, vapour pressure (P^*), absolute temperature, log(vapour pressure), inverse of absolute pressure.
   2. Create a plot of log(P^*) versus inverse of absolute temperature.
   3. Generate a linear trendline through the data.  Get Excel (or any graphing software you are using) to show the trendline equation on the plot.  Clearly state the values of A and B of equation (2) above.
   4. State the relationship between log(P^*) and 1/T.
   5. Use this equation to predict the following:
      1. Vapour pressure of methanol at 50°C, and at 70°C
      2. The boiling temperature of methanol at 0.5 atm, 1 atm, and 1,2 atm
   6. Comment on how the boiling point at 1 atm compares with the literature NBP (normal boiling point) of methanol.
   7. Calculate the vapour pressure of methanol at 50°C and at 70°C using Antoine’s equation (if covered in class) and compare with your predictions during step 6 above.