6 Simple Interest
Chapter 6 Topics
6.1 Principal, Rate, Time
6.2 Moving Money Involving Simple Interest
6.3 Savings Accounts and Short-Term GICs
If you have a lot of surplus cash, it would hardly make sense to hide it under your mattress or bury it in the backyard of your townhouse. As any investment specialist will tell you, you want your money to work for you instead of just sitting idle. So you can invest and be rewarded by earning interest.
Do you know if your account at the Royal Bank of Canada (RBC) has paid you the right amount of interest? You might assume that because everything at a bank is fully automated it is guaranteed to be correct. However, ultimately all automation at the Royal Bank relies on input by an employee. What if your interest rate is keyed in wrong? Maybe the computer programmer erred in a line of computer code and the amount of interest is miscalculated. What if RBC had a computer glitch? These pitfalls highlight the importance of always checking your account statements.
In business, it would be rare for an organization to borrow or lend money for free. That is not to say that businesses are ruthless with each other; in the previous chapter, you saw that most business transactions are completed through interest-free credit transactions involving invoicing. However, this generosity does not extend indefinitely. After the credit period elapses, the business essentially treats an unpaid invoice as a loan and starts charging an interest penalty.
When businesses need to borrow money, promissory notes, demand loans, and commercial papers are just three of the possibilities discussed later in this chapter.
Even governments need to borrow money. Have you ever thought about how the government of Canada or your provincial government goes about doing that? While a government has many methods at its disposal, a common method is to use treasury bills—in essence, borrowing the money from investors.
On a personal level, almost all people invest and borrow money at some time. This chapter examines consumer lines of credit and student loans, both of which carry simple interest rates. On the earnings side, it is common for people to have savings accounts that earn low rates of interest. Other short-term investments include treasury bills, commercial papers, and short-term guaranteed investment certificates (GICs).
The bottom line is that money does not come free. In this chapter, you will explore the concept of simple interest, learn how to calculate it, and then apply simple interest to various financial tools.
6.1 Principal, Rate, Time
Your investments may be at risk if stock and bond markets slump, as a story in the Globe and Mail predicts. You wonder if you should shift your money into relatively secure short-term investments until the market booms again. You consider your high-interest savings account, but realize that only the first $60,000 of your savings account is insured. Perhaps you should put some of that money into treasury bills instead.
Looking ahead, what income will you live on once you are no longer working? As your career develops, you need to save money to fund your lifestyle in retirement. Some day you will have $100,000 or more that you must invest and reinvest to reach your financial retirement goals.
To make such decisions, you must first understand how to calculate simple interest. Second, you need to understand the characteristics of the various financial options that use simple interest. Armed with this knowledge, you can make smart financial decisions!
The world of finance calculates interest in two different ways:
- Simple Interest. A simple interest system primarily applies to short-term financial transactions, with a time frame of less than one year. In this system, which is explored in this chapter, interest accrues but does not compound.
- Compound Interest. A compound interest system primarily applies to long-term financial transactions, with a time frame of one year or more. In this system, which the next chapter explores, interest accrues and compounds upon previously earned interest.
Simple Interest
In a simple interest environment, you calculate interest solely on the amount of money at the beginning of the transaction. When the term of the transaction ends, you add the amount of the simple interest to the initial amount. Therefore, throughout the entire transaction the amount of money placed into the account remains unchanged until the term expires. It is only on this date that the amount of money increases. Thus, an investor has more money or a borrower owes more money at the end.
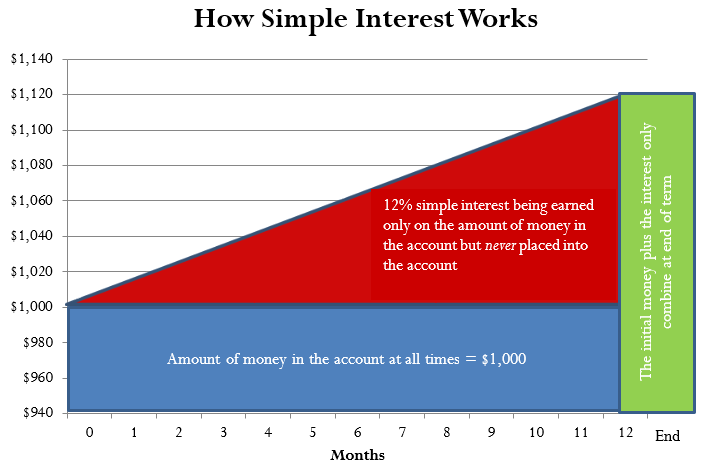
The figure illustrates the concept of simple interest. In this example, assume $1,000 is placed into an account with 12% simple interest for a period of 12 months. For the entire term of this transaction, the amount of money in the account always equals $1,000. During this period, interest accrues at a rate of 12%, but the interest is never placed into the account. When the transaction ends after 12 months, the $120 of interest and the initial $1,000 are then combined to total $1,120.
A loan or investment always involves two parties—one giving and one receiving. No matter which party you are in the transaction, the amount of interest remains unchanged. The only difference lies in whether you are earning or paying the interest.
- If you take out a personal loan from a bank, the bank gives you the money and you receive the money. In this situation, the bank earns the simple interest and you are being charged simple interest on your loan. In the figure, this means you must pay back not only the $1,000 you borrowed initially but an additional $120 in interest.
- If you place your money into an investment account at the bank, you have given the money and the bank has received the money. In this situation, you earn the simple interest on your money and the bank pays simple interest to your investment account. In the figure, this means the bank must give you back your initial $1,000 at the end plus an additional $120 of interest earned.
The Formula
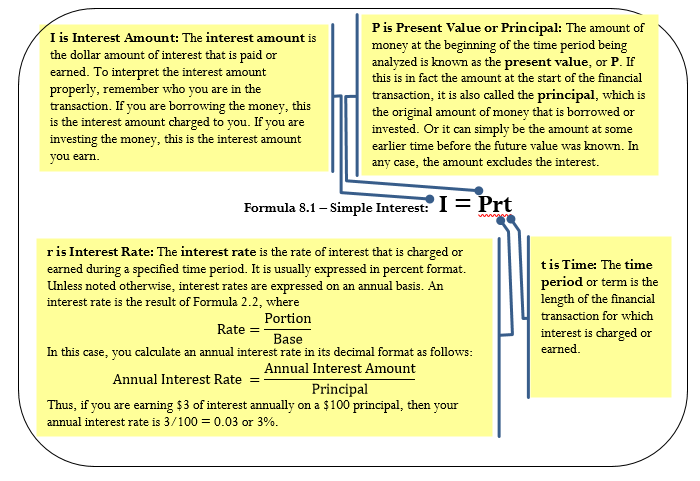
The best way to understand how simple interest is calculated is to think of the following relationship:
Amount of simple interest = How much at What simple interest rate for How long
Notice that the key variables are the amount, the simple interest rate, and time. Formula 6.1 combines these elements into a formula for simple interest.
Simple Interest
How It Works
Follow these steps when you calculate the amount of simple interest:
Step 1: Formula 6.1 has four variables, and you need to identify three for any calculation involving simple interest. If necessary, draw a timeline to illustrate how the money is being moved over time.
Step 2: Ensure that the simple interest rate and the time period are expressed with a common unit. If they are not already, you need to convert one of the two variables to the same units as the other.
Step 3: Apply Formula 6.1 and solve for the unknown variable. Use algebra to manipulate the formula if necessary.
Assume you have $500 earning 3% simple interest for a period of nine months. How much interest do you earn?
Step 1: Note that your principal is $500, or P = $500. The interest rate is assumed to be annual, so r = 3% per year. The time period is nine months.
Step 2: Convert the time period from months to years: t = ![]()
Step 3: According to Formula 6.1, I = $500 × 3% × ![]()
= $11.25. Therefore, the amount of interest you earn on the $500 investment over the course of nine months is $11.25.
Important Notes
Recall that algebraic equations require all terms to be expressed with a common unit. This principle remains true for Formula 6.1, particularly with regard to the interest rate and the time period. For example, if you have a 3% annual interest rate for nine months, then either
- The time needs to be expressed annually as 9/12 of a year to match the yearly interest rate, or
- The interest rate needs to be expressed monthly as 3%/12 = 0.25% per month to match the number of months.
Paths To Success
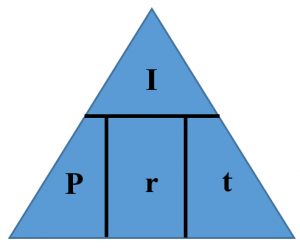
Four variables are involved in the simple interest formula, which means that any three can be known, requiring you to solve for the fourth missing variable. To reduce formula clutter, the triangle technique illustrated here helps you remember how to rearrange the formula as needed.
Give It Some Thought
- If you have money in your savings account (or any other investment) and it earns simple interest over a period of time, would you have more or less money in your account in the future?
- If you have a debt for which you haven’t made any payments, yet it is being charged simple interest on the principal, would you owe more or less money in the future?
Solutions:
1. More, because the interest is earned and therefore is added to your savings account.
2. More, because you owe the principal and you owe the interest, which increases your total amount owing.

|
Julio borrowed $1,100 from Maria five months ago. When he first borrowed the money, they agreed that he would pay Maria 5% simple interest. If Julio pays her back today, how much interest does he owe her?
|
|
|---|---|
|
Calculate the amount of interest that Julio owes Maria (I).
|
|
|
What You Already Know Step 1: The terms of their agreement are as follows: P = $1,100 r = 5% t = 5 months
|
How You Will Get There Step 2: The rate is annual, and the time is in months. Convert the time to an annual number. Step 3: Apply Formula 6.1.
|
|
Step 2: Five months out of 12 months in a year is Step 3: I = $1,100 × 5% × = $1,100 × 0.05 ×
|
|
|
For Julio to pay back Maria, he must reimburse her for the $1,100 principal borrowed plus an additional $22.92 of simple interest as per their agreement.
|
|
Example 6.1B: Do You Know Your Interest Rate?

|
A $3,500 investment earned $70 of interest over the course of six months. What annual rate of simple interest did the investment earn?
|
|
|---|---|
|
Calculate the annual interest rate (r).
|
|
|
What You Already Know Step 1: The principal, interest amount, and time are known: P = $3,500 I = $70 t = 6 months
|
How You Will Get There Step 2: The computed interest rate needs to be annual, so you must express the time period annually as well. Step 3: Apply Formula 6.1, rearranging for r.
|
|
Step 2: Six months out of 12 months in a year is Step 3: $70 = $3,500 × r ×
|
|
|
For $3,500 to earn $70 simple interest over the course of six months, the annual simple interest rate must be 4%.
|
|
Example 6.1C: What Did You Start with?

|
What amount of money invested at 6% annual simple interest for 11 months earns $2,035 of interest?
|
|
|---|---|
|
Calculate the amount of money originally invested, which is known as the present value or principal, symbolized by P.
|
|
|
What You Already Know Step 1: The interest rate, time, and interest earned are known: r = 6% t = 11 months I = $2,035
|
How You Will Get There Step 2: Convert the time from months to an annual basis to match the interest rate. Step 3: Apply Formula 6.1, rearranging for P.
|
|
Step 2: Eleven months out of 12 months in a year is Step 3: $2,035 = P × 6% ×
|
|
|
To generate $2,035 of simple interest at 6% over a time frame of 11 months, $37,000 must be invested.
|
|
|
For how many months must $95,000 be invested to earn $1,187.50 of simple interest at an interest rate of 5%?
|
|
|---|---|
|
Calculate the length of time in months (t) that it takes the money to acquire the interest.
|
|
|
What You Already Know Step 1: The amount of money invested, interest earned, and interest rate are known: P = $95,000.00 I = $1,187.50 r = 5%
|
How You Will Get There Step 2: Express the time in months. Convert the interest rate to a "per month" format. Step 3: Apply Formula 6.1, rearranging for t.
|
|
Step 2: 5% per year converted into a monthly rate is r = Step 3:
|
|
|
For $95,000 to earn $1,187.50 at 5% simple interest, it must be invested for a three-month period.
|
|
Time and Dates
In the examples of simple interest so far, the time period equalled an exact number of months. While this is convenient in many situations, financial institutions and organizations calculate interest based on the exact number of days in the transaction, which changes the interest amount.
To illustrate this, assume you had money saved for the entire months of July and August, where t = ![]() or t = 0.1
or t = 0.1 ![]() of a year. However, if you use the exact number of days, the 31 days in July and 31 days in August total 62 days. In a 365-day year that is t =
of a year. However, if you use the exact number of days, the 31 days in July and 31 days in August total 62 days. In a 365-day year that is t = ![]() %
%
or t = 0.169863 of a year. Notice a difference of 0.003196 occurs. Therefore, to be precise in performing simple interest calculations, you must calculate the exact number of days involved in the transaction.
Figuring Out the Days
In practice, when counting the number of days in a transaction you include the first day but not the last day. This is because interest is calculated on the daily closing balance, not on interim balances throughout a day. For example, if you borrowed $500 on June 3 and paid it back with interest on June 5, the closing balance on June 3 and June 4 is $500. However, on June 5 a zero balance is restored. Therefore, you count June 3 and 4 as days of interest but not June 5, so you will owe two days of interest, not three.
There are three common ways to calculate the number of days involved in a transaction.
Method 1: Use Your Knuckles
You can use your knuckles as an aid to remembering which months of the year have more or fewer days.
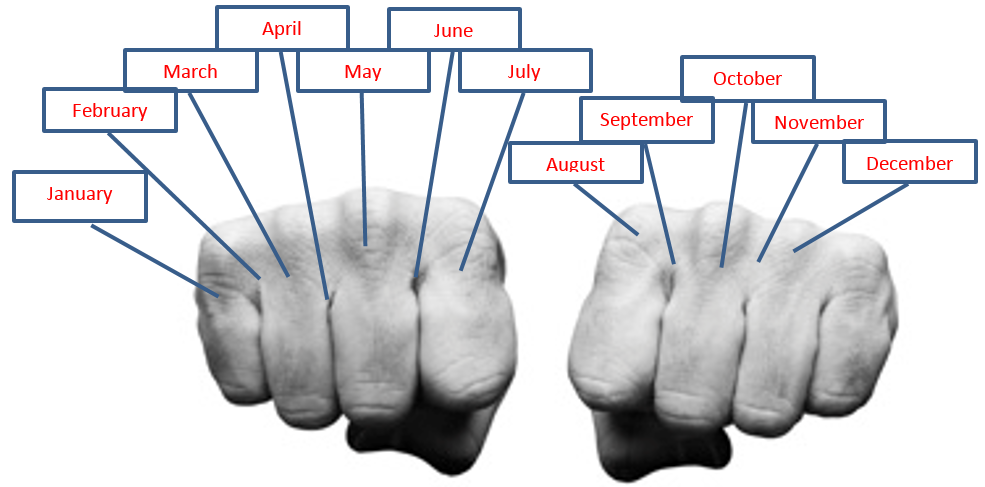
Put your knuckles side by side and start on your outermost knuckle. Every knuckle represents a month with 31 days. Every valley between the knuckles represents a month that does not have 31 days (30 in all except February, which has 28 or 29). Now start counting months. Your first knuckle (pinkie finger) is January, which has 31 days. Next is your first valley, which is February and it does not have 31 days. Your next knuckle (ring finger) is March, which has 31 days … and so on. When you get to your last knuckle (your index finger), move to the other hand’s first knuckle (an index finger again). Notice that July and August are the two months back to back with 31 days.
If you are trying to calculate the number of days between March 20 and May 4, use your knuckles to recall that March has 31 days and April has 30 days. The calculations are illustrated in the table here.
|
Start |
End |
Days |
|
March |
March 31 |
31 − 20 = 11 days |
|
March |
April 30 |
30 − 0 = 30 days |
|
April |
May 4 |
4 − 0 = 4 days |
|
TOTAL |
11 + 30 + 4 = 45 |
|
Why does the end date of one line become the start date of the next line? Recall that you count the first day, but not the last day. Therefore, on the first line March 31 has not been counted yet and must be counted on the second line. Ultimately a transaction extending from March 20 to May 4 involves 45 days as the time period.
Method 2: Use A Table of Serial Numbers
In the table on the next page, the days of the year are assigned a serial number. The number of days between any two dates in the same calendar year is simply the difference between the serial numbers for the dates.
Using the example in Method 1, when the dates are within the same calendar year, find the serial number for the later date, May 4 (Day 124) and the serial number for the earlier date, March 20 (Day 79). Then, find the difference between the two serial numbers (124 – 79 = 45 days).

*For Leap years, February 29 becomes Day 60 and the serial number for each subsequent day is increased by 1.
Method 3: Use The BAII Plus Date Function
Your BAII Plus calculator is programmed with the ability to calculate the number of days involved in a transaction according to the principle of counting the first day but not the last day. The function “Date” is located on the second shelf above the number one. To use this function, open the window by pressing 2nd 1.
- Scroll amongst the four display lines by using your ↑ and ↓ arrows. There are four variables:
- DT1 is the starting date of the transaction.
- DT2 is the ending date of the transaction.
- DBD is the days between dates, which is your t in Formula 6.1.

4. ACT or 360 is the method of calculating the days between dates. In ACT (for “actual”), the calculator calculates the DBD based on the correct number of days in the month. In 360, the DBD is based on treating every month as having 30 days (30 × 12 = 360 days). For all calculations, set the calculator to the ACT mode. Toggle this setting by pressing 2nd SET.
- To enter a date into the calculator, the calculator uses the format of MM.DDYY where:
- MM is the numerical value of the month; you do not need to enter the leading zero on months with only one digit.
- DD is the day of the month; you must always enter this value with two digits using a leading zero for days 1 through 9 in a month.
- YY is the last two digits of the year; you must always enter this with two digits. If your question does not involve a year, select an appropriate year of your choice.
- As long as you know any two of the DT1, DT2, or DBD variables, you can calculate the third. Enter any two of the three variables, pressing ENTER after each and ensuring the window shows the output variable you are seeking, and then press CPT.
Using the example in Method 1, to calculate the time from March 20 to May 4 you first need to choose a year arbitrarily, perhaps 2011. Therefore, perform the following sequence:
2nd DATE
2nd CLR Work (to erase previous calculations)
3.2011 ENTER ↓ (this is March 20, 2011)
5.0411 ENTER ↓ (this is May 4, 2011)
CPT
Answer: 45
Note that the answer is the same as the one you arrived at manually using your knuckles.
Important Notes
When solving for t, decimals may appear in your solution. For example, if calculating t in days, the answer may show up as 45.9978 or 46.0023 days; however, interest is calculated only on complete days. This occurs because the interest amount (I) used in the calculation has been rounded off to two decimals. Since the interest amount is imprecise, the calculation of t is imprecise. When this occurs, round t off to the nearest integer.
Things To Watch Out For
Miscalculating the number of days in February has to be one of the most common errors. To help you remember how many days are in February, recall your knowledge of leap years.
- February has 28 days except for leap years, in which it has 29 days.
- Leap years are those years that are evenly divisible by four or 400. However, those years that are evenly divisible by 100 (excepting years that are evenly divisible by 400) are not leap years. Here are some examples to illustrate this rule:
- The year 1900 was not a leap year, since it is evenly divisible by 100 and not by 400.
- The year 1996 was a leap year, since it is evenly divisible by four and not by 100.
- The year 2000 was one of those exception years, and it was a leap year since it is evenly divisible by 400.
- The year 2004 was once again a leap year since it is evenly divisible by four and not by 100. Thus, in this century 2004, 2008, 2012, 2016, 2020, 2024, and so on by fours are all leap years with 29 days.
- The year 2100 will not be a leap year, since it is evenly divisible by 100.
Note that when it comes to the total number of days in a year, simple interest calculations ignore the 366th day in a leap year. Therefore, assume a year has 365 days in all calculations.
Paths To Success
When entering two dates either on the calculator or in Excel, the order in which you key in the dates is not important. If you happen to put the last day of the transaction into the first field (DT1 or Start Date) and the start day of the transaction into the last field (DT2 or End Date), then the number of days will compute as a negative number since the dates are reversed. Ignore the negative sign in these instances. Using the example, on your calculator if you had keyed May 4 into DT1 and March 20 into DT2, the DBD computes as −45, in which you ignore the negative sign to determine the answer is 45 days.
Example 6.1E: Time Using Dates

|
Azul borrowed $4,200 from Hannah on November 3, 2011. Their agreement required Azul to pay back the loan on April 14, 2012, with 8% simple interest. In addition to the principal, how much interest does Azul owe Hannah on April 14?
|
||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Calculate the amount of simple interest (I) that Azul owes Hannah on his loan.
|
||||||||||||||||||||||||||
|
What You Already Know Step 1: The principal, simple interest rate, and dates are known: P = $4,200 r = 8% Start Date = November 3, 2011 End Date = April 14, 2012
|
How You Will Get There Step 1 (continued): Calculate the number of days in the transaction. Note that this transaction involves February 2012, which is a leap year. Step 2: The rate is annual and the time is in days. Convert the time to an annual number. Step 3: Apply Formula 6.1.
|
|||||||||||||||||||||||||
|
Step 1 (continued):
Step 2: 163 days out of 365 days in a year is t = Step 3: I = $4,200 × 8% ×
|
||||||||||||||||||||||||||
|
Azul borrowed the money for a period of 163 days and owes Hannah $150.05 of simple interest on his loan, in addition to repaying the principal of $4,200.
|
||||||||||||||||||||||||||
Example 6.1F: Figuring Out Dates Using Time
|
On September 13, 2011, Aladdin decided to pay back the Genie on his loan of $15,000 at 9% simple interest. If he paid the Genie the principal plus $1,283.42 of interest, on what day did he borrow the money from the Genie?
|
||
|---|---|---|
|
To determine the starting date, the time involved in this transaction, or t, must be calculated.
|
||
|
What You Already Know Step 1: The principal, interest amount, simple interest rate, and end date are known: P = $15,000.00 I = $1,283.42 r = 9% End Date = September 13, 2011
|
How You Will Get There Step 2: The time is in days, but the rate is annual. Convert the rate to a daily rate. Step 3: Apply Formula 6.1, rearranging for t. Step 3 (continued): Using the End Date, use the t to determine the Start Date.
|
|
|
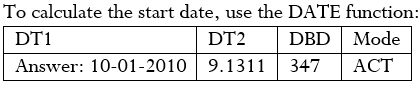
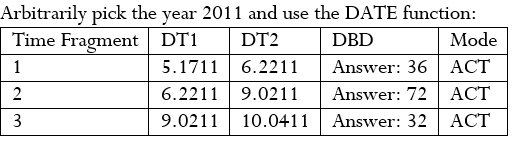
Step 2: Convert the interest rate to daily: r = Step 3: Step 3 (continued): The number of days is close to a year. Go back 365 days and start at September 13, 2010. Notice that 347 days is 365 − 347 = 18 days short of a full year. Adding 18 days onto September 13, 2010, equals October 1, 2010. This is the start date.
|
|
|
|
If Aladdin owed the Genie $1,283.42 of simple interest at 9% on a principal of $15,000, he must have borrowed the money 347 days earlier, which is October 1, 2010.
|
||
Variable Interest Rates
Not all interest rates remain constant. There are two types of interest rates:
- Fixed. A fixed interest rate is an interest rate that is unchanged for the duration of the transaction.
- Variable. A variable interest rate is an interest rate that is open to fluctuations over the duration of a transaction. This variable interest rate is usually tied to the prime rate, which is an interest rate set by the Bank of Canada that usually forms the lowest lending rate for the most secure loans. Most people and companies are usually charged the prime rate plus a percentage (typically 0.5% to 5%) to arrive at the variable interest rate. The Bank of Canada periodically adjusts this rate because of economic and financial considerations in Canada.
In all of the previous examples in this section, the interest rate (r) was fixed for the duration of the transaction. When r fluctuates, you must break the question into time periods or time fragments for each value of r. In each of these time fragments, you calculate the amount of simple interest earned or charged and then sum the interest amounts to form the total interest earned or charged.
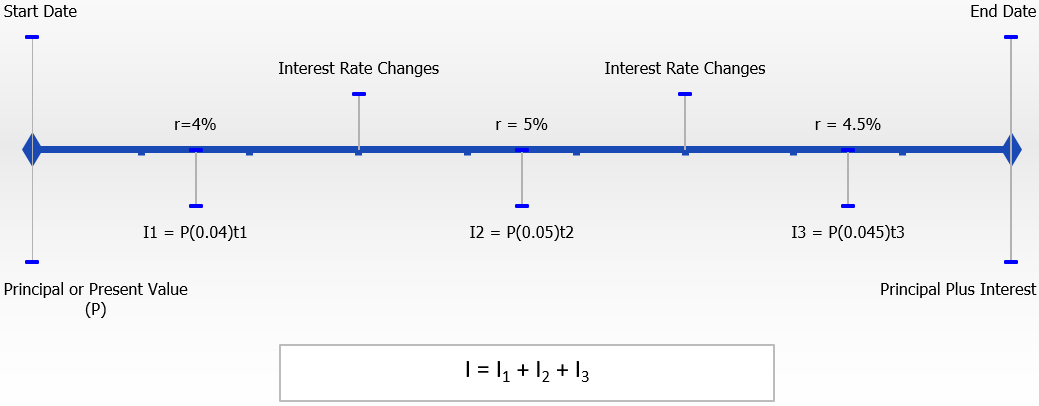
This figure illustrates this process with a variable rate that changes twice in the course of the transaction. To calculate the total interest amount, you need to execute Formula 6.1 for each of the time fragments. Then total the interest amounts from each of the three time fragments to calculate the interest amount (I) for the entire transaction.
Example 6.1G: A Floating Rate
|
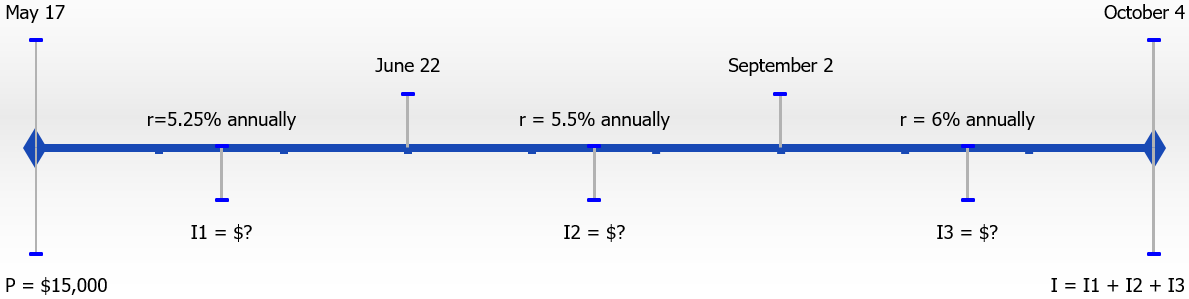
Julio borrowed $10,000 on May 17 at a variable interest rate of prime + 3% when the prime rate was 2¼%. On June 22 the prime rate increased by ¼%, and on September 2 it increased again by ½%. How much interest will Julio pay when he repays his loan on October 4?
|
|||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Calculate the amount of interest that Julio owes for the entire time frame of his loan, or I, from May 17 to October 4.
|
|||||||||||||||||||||||||||||||||
|
What You Already Know Step 1: There is an initial interest rate and then it changes twice over the course of the transaction. That means there are three time periods and three different interest rates. The principal is also known: P = $10,000.
|
How You Will Get There Step 1 (continued): Calculate the number of days for each of the three time periods. Step 2: The rates are annual while each of the times are in days. Convert each of the times to an annual number. Step 3: For each time period, apply Formula 6.1. Step 3 (continued): Sum the three interest amounts to arrive at the total interest paid.
|
||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
|
Calculator Instructions
|
|||||||||||||||||||||||||||||||||
|
Julio owes $319.32 of simple interest on his October 4 repayment date.
|
|||||||||||||||||||||||||||||||||
Exercises
For each of the following questions, round all money to two decimals and percentages to four decimals.
Mechanics
For questions 1–6, solve for the unknown variables (identified with a ?) based on the information provided.
|
|
Interest |
Principal |
Interest |
Time |
|
1. |
? |
$130,000.00 |
8% |
9 |
|
2. |
$4,000.00 |
? |
2% per |
8 |
|
3. |
$1,437.50 |
$57,500.00 |
? per |
4 |
|
4. |
$103.13 |
$1,250.00 |
9% |
? |
|
5. |
? |
$42,250.00 |
1½% |
½ year |
|
6. |
$1,350.00 |
? |
6¾% |
3 |
Applications
- Brynn borrowed $25,000 at 1% per month from a family friend to start her entrepreneurial venture on December 2, 2011. If she paid back the loan on June 16, 2012, how much simple interest did she pay?
- Alex took out a variable rate $20,000 loan on July 3 at prime + 4% when prime was set at 3%. The prime rate increased ½% on August 15. How much simple interest does Alex owe if the loan is paid back on September 29?
- How much simple interest is earned on $50,000 over 320 days if the interest rate is:
- 3%
- 6%
- 9%
- What relationship is evident between simple interest amounts and rates in your three answers above?
- If you placed $2,000 into an investment account earning 3% simple interest, how many months does it take for you to have $2,025 in your account?
- Cuthbert put $15,000 into a nine-month term deposit earning simple interest. After six months he decided to cash the investment in early, taking a penalty of 1% on his interest rate. If he received $393.75 of interest, what was the original interest rate before the penalty on his term deposit?
- If you want to earn $1,000 of simple interest at a rate of 7% in a span of five months, how much money must you invest?
- On March 3, when the posted prime rate was 4%, an investment of $10,000 was placed into an account earning prime + 2½%. Effective June 26, the prime rate rose by ¾%, and on October 4 it rose another ½%. On November 2, it declined by ¼%. If the money was withdrawn on December 15, how much simple interest did it earn?
- If $6,000 principal plus $132.90 of simple interest was withdrawn on August 14, 2011, from an investment earning 5.5% interest, on what day was the money invested?
- Jessica decided to invest her $11,000 in two back-to-back three-month term deposits. On the first three-month term, she earned $110 of interest. If she placed both the principal and the interest into the second three-month term deposit and earned $145.82 of interest, how much higher or lower was the interest rate on the second term deposit?
Challenge, Critical Thinking, & Other Applications
- The simple interest formula applies to any instance of constant unit growth. Assume that 200 units of product are sold today and you forecast a constant 20-unit sales increase every four weeks. What will be the sales in one year’s time (assume a year has exactly 52 weeks)?
- Cade received an invoice for $5,200 dated August 13 with terms of 2/10, net 30 with a stated penalty of 2% simple interest per month. If Cade pays this invoice on December 13, what penalty amount is added to the invoice?
- Marrina is searching for the best way to invest her $10,000. One financial institution offers 4.25% on three-month term deposits and 4.5% on six-month term deposits. Marrina is considering either doing two back-to-back three-month term deposits or just taking the six-month deposit. It is almost certain that interest rates will rise by 0.5% before her first three-month term is up. She will place the simple interest and principal from the first three-month term deposit into the second three-month deposit. Which option should Marrina pursue? How much better is your recommended option?
- Goliath borrowed $20,000 on January 3 at prime + 4.5%. The prime rate changed throughout his term (of a non–leap year) as follows:
|
Date |
Prime |
|
January |
2.25% |
|
February |
2.5% |
|
April |
3% |
|
June |
2.75% |
|
September |
3.25% |
- If he repaid his loan on December 24, what amount of simple interest should Goliath be charged?
- What equivalent fixed rate of simple interest did he get charged on his loan?
- Evaluate each of the following $10,000 investment alternatives and recommend the best alternative for investing any principal regardless of the actual amount. Assume in all cases that the principal and simple interest earned in prior terms are placed into subsequent investments.
|
Alternative |
Alternative |
Alternative |
|
6% |
5% 7% for 6 months |
5.25% 5.75% 6.25% 6.75% for 3 months |
What percentage more interest is earned in the best alternative versus the worst alternative?
6.2 Moving Money Involving Simple Interest
Can you calculate the amount of money required to meet a future goal? Assume you will graduate college with your business administration diploma in a few months and have already registered at your local university to continue with your studies toward a bachelor of commerce degree. You estimate your total tuition, fees, and textbooks at $8,000. After investigating some short-term investments, you find the best simple rate of interest obtainable is 4.5%. How much money must you invest today for it to grow with interest to the needed tuition money?
In the previous section, you calculated the amount of interest earned or charged on an investment or loan. While this number is good to know, most of the time investors are interested solely in how much in total, including both principal and interest, is either owed or saved. Also, to calculate the interest amount in Formula 6.1, you must know the principal. When people plan for the future, they know the future amount of money that they need but do not know how much money they must invest today to arrive at that goal. This is the case in the opening example above, so you need a further technique for handling simple interest.
This section explores how to calculate the principal and interest together in a single calculation. It adds the flexibility of figuring out how much money there is at the beginning of the time period so long as you know the value at the end, or vice versa. In this way, you can solve almost any simple interest situation.
Maturity Value (or Future Value)
The maturity value of a transaction is the amount of money resulting at the end of a transaction, an amount that includes both the interest and the principal together. It is called a maturity value because in the financial world the termination of a financial transaction is known as the “maturing” of the transaction. The amount of principal with interest at some point in the future, but not necessarily the end of the transaction, is known as the future value.
Simple Interest for Single Payments

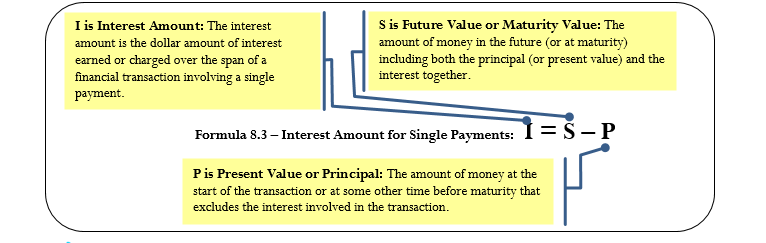
Depending on the financial scenario, what information you know, and what variable you need to calculate, you may need a second formula offering an alternative method of calculating the simple interest dollar amount.
Interest Amount
How It Works
Follow these steps when working with single payments involving simple interest:
Step 1: Formula 6.2 has four variables, any three of which you must identify to work with a single payment involving simple interest.
- If either the P or S is missing but the I is known, apply Formula 6.3 to determine the unknown value.
- If only the interest amount I is known and neither P nor S is identified, recall that the interest amount is a portion and that the interest rate is a product of rate and time (e.g., 6% annually for nine months is an earned interest rate of 4.5%). Apply Formula 2.2 on rate, portion, and base to solve for base, which is the present value or P.
- If necessary, draw a timeline to illustrate how the money is being moved through time.
Step 2: Ensure that the simple interest rate and the time period are expressed with a common unit. If not, you need to convert one of the two variables to achieve the commonality.
Step 3: Apply Formula 6.2 and solve for the unknown variable, manipulating the formula as required.
Step 4: If you need to calculate the amount of interest, apply Formula 6.3.
Assume that today you have $10,000 that you are going to invest at 7% simple interest for 11 months. How much money will you have in total at the end of the 11 months? How much interest do you earn?
Step 1: The principal is P = $10,000, the simple interest rate is 7% per year, or r = 0.07, and the time is t = 11 months.
Step 2: The time is in months, but to match the rate it needs to be expressed annually as t = ![]()
Step 3: Applying Formula 6.2 to calculate the future value including interest,
S = $10,000 × (1 + 0.07 × ![]()
) = $10,641.67. This is the total amount after 11 months.
Step 4: Applying Formula 6.3 to calculate the interest earned, I = $10,641.67 − $10,000.00 = $641.67. You could also apply Formula 6.1 to calculate the interest amount; however, Formula 6.3 is a lot easier to use. The $10,000 earns $641.67 in simple interest over the next 11 months, resulting in $10,641.67 altogether.
Things To Watch Out For
As with Formula 6.1, the most common mistake in the application of Formula 6.2 is failing to ensure that the rate and time are expressed in the same units. Before you proceed, always check these two variables!
Paths To Success
When solving Formula 6.2 for either rate or time, it is generally easier to use Formulas 6.3 and 6.1 instead. Follow these steps to solve for rate or time:
- If you have been provided with both the present value and future value, apply Formula 6.3 to calculate the amount of interest (I).
- Apply and rearrange Formula 6.1 to solve for either rate or time as required.
Give It Some Thought
In each of the following situations, determine which statement is correct.
- If you have a future value of $5,000 and interest is involved, then your present value is
- More than $5,000
- The same
- Less than $5,000
- If you had a principal of $10,000 earning 10% simple interest for any period less than a year, you earn
- More than $1,000 interest
- Exactly $1,000 interest
- Less than $1,000 interest
- If you took out a loan for $2,500 at a 5% simple interest rate for six months and you made no payments during that time frame, you owe
- More than $2,500
- Exactly $2,500
Solutions: Less than $5,000. When being charged or earning interest, the present value is always less than the future value. Less than $1,000 interest. The $10,000 earns exactly $1,000 interest per year, so any time frame less than a year produces a smaller interest amount.More than $2,500. When interest is being charged, the future value is always larger than the present value.
Less than $2,500
Example 6.2A: Saving for a Down Payment on a Home

|
You just inherited $35,000 from your uncle's estate and plan to purchase a house four months from today. If you use your inheritance as your down payment on the house, how much will you be able to put down if your money earns 4¼% simple interest? How much interest will you have earned?
|
|
|---|---|
|
Calculate the amount of money four months from now including both the principal and interest earned. This is the maturity value (S). Also calculate the interest earned (I).
|
|
|
What You Already Know Step 1: The principal, interest rate, and time frame are known: P = $35,000 r = 4¼% per year t = 4 months
|
How You Will Get There Step 2: While the rate is annual, the time is in months. Convert the time to an annual number. Step 3: Apply Formula 6.2. Step 4: Apply Formula 6.3 to calculate the interest amount.
|
|
Step 2: Four months out of 12 months in a year is t = Step 3: S = $35,000 × (1 + 4¼% × Step 4: I = $35,495.83 − $35,000.00 = $495.83
|
|
|
Four months from now you will have $35,495.83 as a down payment toward your house, which includes $35,000 in principal and $495.83 of interest.
|
|
Example 6.2B: Saving for Tuition

|
Recall the section opener, where you needed $8,000 for tuition in the fall and the best simple interest rate you could find was 4.5%. Assume you have eight months before you need to pay your tuition. How much money do you need to invest today?
|
|
|---|---|
|
Calculate the principal amount of money today (P) that you must invest such that it will earn interest and end up at the $8,000 required for the tuition.
|
|
|
What You Already Know Step 1: The future value, interest rate, and time period are known: S = $8,000 r = 4.5% per year t = 8 months
|
How You Will Get There Step 2: While the rate is annual, the time is in months. Convert the time to an annual number. Step 3: Apply Formula 6.2, rearranging for P.
|
|
Step 2: Eight months out of 12 months in a year is t = Step 3: $8,000 = P(1 + 4.5% ×
|
|
|
If you place $7,766.99 into the investment, it will grow to $8,000 in the eight months.
|
|
Example 6.2C: What Exactly Are You Being Offered?
|
You are sitting in an office at your local financial institution on August 4. The bank officer says to you, "We will make you a great deal. If we advance that line of credit and you borrow $20,000 today, when you want to repay that balance on September 1 you will only have to pay us $20,168.77, which is not much more!" Before answering, you decide to evaluate the statement. Calculate the simple interest rate that the bank officer used in her calculations.
|
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Determine the rate of interest that you would be charged on your line of credit, or r.
|
||||||||||||||
|
What You Already Know Step 1: The principal, maturity amount, and time frame are known: P = $20,000.00 S = $20,168.77 t = August 4 to September 1
|
How You Will Get There Step 1 (continued): Calculate the number of days in the transaction. Step 2: Since interest rates are usually expressed annually, convert the time from days to an annual number. Step 3: Use the combination of Formulas 6.3 and 6.1. First calculate the interest amount using Formula 6.3. Step 3 (continued): Then apply Formula 6.1, rearranging for r.
|
|||||||||||||
|
Step 1 (continued):
Step 2: 28 days out of 365 days in a year is t = Step 3: I = $20,168.77 − $20,000.00 = $168.77 Step 3 (continued):
|
||||||||||||||
|
The interest rate on the offered line of credit is 11.0002% (note that it is probably exactly 11%; the extra 0.0002% is most likely due to the rounded amount of interest used in the calculation).
|
||||||||||||||

Equivalent Payments
Life happens. Sometimes the best laid financial plans go unfulfilled. Perhaps you have lost your job. Maybe a reckless driver totalled your vehicle, which you now have to replace at an expense you must struggle to fit into your budget. No matter the reason, you find yourself unable to make your debt payment as promised.
On the positive side, maybe you just received a large inheritance unexpectedly. What if you bought a scratch ticket and just won $25,000? Now that you have the money, you might want to pay off that debt early. Can it be done?
Whether paying late or paying early, any amount paid must be equivalent to the original financial obligation. As you have learned, when you move money into the future it accumulates simple interest. When you move money into the past, simple interest must be removed from the money. This principle applies both to early and late payments:
- Late Payments. If a debt is paid late, then a financial penalty that is fair to both parties involved should be imposed. That penalty should reflect a current rate of interest and be added to the original payment. Assume you owe $100 to your friend and that a fair current rate of simple interest is 10%. If you pay this debt one year late, then a 10% late interest penalty of $10 should be added, making your debt payment $110. This is no different from your friend receiving the $100 today and investing it himself at 10% interest so that it accumulates to $110 in one year.
- Early Payments. If a debt is paid early, there should be some financial incentive (otherwise, why bother?). Therefore, an interest benefit, one reflecting a current rate of interest on the early payment, should be deducted from the original payment. Assume you owe your friend $110 one year from now and that a fair current rate of simple interest is 10%. If you pay this debt today, then a 10% early interest benefit of $10 should be deducted, making your debt payment today $100. If your friend then invests this money at 10% simple interest, one year from now he will have the $110, which is what you were supposed to pay.
Notice in these examples that a simple interest rate of 10% means $100 today is the same thing as having $110 one year from now. This illustrates the concept that two payments are equivalent payments if, once a fair rate of interest is factored in, they have the same value on the same day. Thus, in general you are finding two amounts at different points in time that have the same value, as illustrated in the figure below.

How It Works
The steps required to calculate an equivalent payment are no different from those for single payments. If an early payment is being made, then you know the future value, so you solve for the present value (which removes the interest). If a late payment is being made, then you know the present value, so you solve for the future value (which adds the interest penalty).
Paths To Success
Being financially smart means paying attention to when you make your debt payments. If you receive no financial benefit for making an early payment, then why make it? The prudent choice is to keep the money yourself, invest it at the best interest rate possible, and pay the debt off when it comes due. Whatever interest is earned is yours to keep and you still fulfill your debt obligations in a timely manner!
Example 6.2D: Making a Late Payment

|
Erin owes Charlotte $1,500 today. Unfortunately, Erin had some unexpected expenses and is unable to make her debt payment. After discussing the issue, they agree that Erin can make the payment nine months late and that a fair simple interest rate on the late payment is 5%. How much does Erin need to pay nine months from now? What is the amount of her late penalty?
|
|
|---|---|
|
A late payment is a future value amount (S). The late penalty is equal to the interest (I).
|
|
|
What You Already Know Step 1: The payment today, the agreed-upon interest rate, and the late payment timing are known: P = $1,500 r = 5% annually t = 9 months
|
How You Will Get There Step 2: While the rate is annual, the time is in months. Convert the time to an annual number. Step 3: Apply Formula 6.2. Step 4: Apply Formula 6.3 to calculate the late interest penalty amount.
|
|
Step 2: Nine months out of 12 months in a year is t = Step 3: S = $1,500 × (1 + 5% × Step 4: I = $1,556.25 − $1,500.00 = $56.25
|
|
|
Erin's late payment is for $1,556.25, which includes a $56.25 interest penalty for making the payment nine months late.
|
|
Example 6.2E: Making an Early Payment

|
Rupert owes Aminata two debt payments: $600 four months from now and $475 eleven months from now. Rupert came into some money today and would like to pay off both of the debts immediately. Aminata has agreed that a fair interest rate is 7%. What amount should Rupert pay today? What is the total amount of his early payment benefit?
|
||
|---|---|---|
|
An early payment is a present value amount (P). Both payments will be moved to today and summed. The early payment benefit will be the total amount of interest removed (I).
|
||
|
What You Already Know Step 1: The two payments, interest rate, and payment due dates are known: r = 7% annually First Payment: S = $600 t = 4 months from now Second Payment: S = $475 t = 11 months from now Replacement payment is being made today.
|
How You Will Get There Do steps 2 and 3 for each payment: Step 2: While the rate is annual, the time is in months. Convert the time to an annual number. Step 3: Apply Formula 6.2, rearranging it to solve for P. Once you calculate both P, they can be summed to arrive at the total payment. Step 4: For each payment, apply Formula 6.3 to calculate the associated early interest benefit. Total the two values of I to get the early interest benefit overall.
|
|
|
Payment #1: Step 2: Four months out of 12 months in a year is t = Step 3: $600 = P (1 + 7% ×
Payment #2: Step 2: Eleven months out of 12 months in a year is t = Step 3: $475 = P (1 + 7% ×
|
Totals: P today = $586.32 + $446.36 = $1,032.68
Step 4: Payment #1: I=S–P = $600 – $586.32 = $13.68 Payment #2: I=S–P = $475 – $446.36 = $28.64
I = $13.68 + $28.64 = $42.32
|
|
|
To clear both debts today, Rupert pays $1,032.68, which reflects a $42.32 interest benefit reduction for the early payment.
|
||
Exercises
For each of the following questions, round all money to two decimals and percentages to four decimals.
Mechanics
For questions 1–4, solve for the unknown variables (identified with a ?) based on the information provided.
|
|
Interest Amount |
Principal / Present Value |
Interest Rate |
Time |
Maturity / Future Value |
|
1. |
? |
$16,775.00 |
0.5% per month |
6 months |
? |
|
2. |
? |
? |
9% |
2 months |
$61,915.00 |
|
3. |
$1,171.44 |
? |
5¾% |
? months |
$23,394.44 |
|
4. |
$2,073.67 |
$41,679.00 |
? |
227 days |
? |
Questions 5–8 involve either early or late payments. Calculate the following for each:
- The dollar amount of the early or late payment
- The amount of interest that forms the late penalty or early benefit
|
|
Original Payments |
Proposed Payments |
Interest Rate |
|
5. |
$1,700 today |
Seven months from today |
8% |
|
6. |
$3,800 two years from now |
Today |
6.35% |
|
7. |
$950 two months from now; $1,000 seven months from now |
A single payment one year from now |
4.95% |
|
8. |
$2,150 three months from now; $1,875 thirteen months from now |
A single payment today |
11% |
Applications
- On January 23 of a non–leap year, a loan is taken out for $15,230 at 8.8% simple interest. What is the maturity value of the loan on October 23?
- An accountant needs to allocate the principal and simple interest on a loan payment into the appropriate ledgers. If the amount received was $10,267.21 for a loan that spanned April 14 to July 31 at 9.1%, how much was the principal and how much was the interest?
- Suppose Robin borrowed $3,600 on October 21 and repaid the loan on February 21 of the following year. What simple interest rate was charged if Robin repaid $3,694.63?
- How many weeks will it take $5,250 to grow to $5,586 at a simple interest rate of 10.4%? Assume 52 weeks in a year.
- Jayne needs to make three payments to Jade requiring $2,000 each 5 months, 10 months, and 15 months from today. She proposes instead making a single payment eight months from today. If Jade agrees to a simple interest rate of 9.5%, what amount should Jayne pay?
- Markus failed to make three payments of $2,500 scheduled one year ago, nine months ago, and six months ago. As his creditor has successfully sued Markus in small claims court, the judge orders him to pay his debts. If the court uses a simple interest rate of 1.5% per month, what amount should the judge order Markus to pay today?
Challenge, Critical Thinking, & Other Applications
- Over a period of nine months, $40.85 of simple interest is earned at 1.75% per quarter. Calculate both the principal and maturity value for the investment.
- The Home Depot is clearing out lawn mowers for $399.75 in an end-of-season sale that ends on September 30. Alternatively, you could wait until April 1 (assume February is in a non–leap year) and pay $419.95 on the same lawn mower. Assume your money can earn simple interest of 4.72% on a short-term investment.
- Which option should you choose?
- How much money will you have saved on September 30 by making that choice?
- Tula lent $15,000 to a business associate on August 12 at 6% simple interest. The loan was to be repaid on November 27; however, the business associate was unable to make the payment. As a consequence, they agreed that the associate could repay the debt on December 29 and that Tula would add $200 to the balance that was due on November 27. What rate of simple interest is Tula charging on the late payment?
- Merina is scheduled to make two loan payments to Bradford in the amount of $1,000 each, two months and nine months from now. Merina doesn’t think she can make those payments and offers Bradford an alternative plan where she will pay $775 seven months from now and another payment seven months later. Bradford determines that 8.5% is a fair interest rate. What is the amount of the second payment?
- Alia took out three back-to-back short-term simple interest investments. On November 10, Alia had saved up a total of $12,986.75. Her interest rate for each investment is listed below:
|
Dates |
Interest Rate |
|
March 2 to June 19 |
4.13% |
|
June 19 to October 7 |
4.63% |
|
October 7 to November 10 |
4.43% |
How much did Alia originally invest on March 2? Assume that the principal and interest from a prior investment are both placed into the next investment.
- An accountant just received a payment from a client on January 26 in the amount of $14,500. The cheque stub states the payment is to be applied toward the client’s three outstanding loans. The three loans were for $4,500 on May 12, $6,750 on July 11, and $8,000 on August 23. All loans are being charged simple interest of 6.85%. What is the remaining balance on the client’s account?
6.3 Application: Savings Accounts and Short-Term GICs
When the stock market offers potentially huge returns, why would anyone put money into an investment that earns just a few percent annually? The answer of course is that sometimes stocks decrease in value. For example, after reaching a historic high in June 2008, the Toronto Stock Exchange plunged 40% over the course of the next six months. So if you are not willing to take the risk in the stock market, there are many options for investing your money that are safe and secure, particularly savings accounts and short-term guaranteed investment certificates (GICs). Some of the benefits and drawbacks associated with safe and secure investments are listed in the table below.
| Benefits | Drawbacks |
|
|
Savings Accounts
A savings account is a deposit account that bears interest and has no stated maturity date. These accounts are found at most financial institutions, such as commercial banks (Royal Bank of Canada, TD Canada Trust, etc.), trusts (Royal Trust, Laurentian Trust, etc.), and credit unions (FirstOntario, Steinbach, Assiniboine, Servus, etc.). Owners of such accounts make deposits to and withdrawals from these accounts at any time, usually accessing the account at an automatic teller machine (ATM), at a bank teller, or through online banking.
A wide variety of types of savings accounts are available. This textbook focuses on the most common features of most savings accounts, including how interest is calculated, when interest is deposited, insurance against loss, and the interest rate amounts available.
- How Interest Is Calculated. There are two common methods for calculating simple interest:
- Accounts earn simple interest that is calculated based on the daily closing balance of the account. The closing balance is the amount of money in the account at the end of the day. Therefore, any balances in the account throughout a single day do not matter. For example, if you start the day with $500 in the account and deposit $3,000 at 9:00 a.m., then withdraw the $3,000 at 4:00 p.m., your closing balance is $500. That is the principal on which interest is calculated, not the $3,500 in the account throughout the day.
- Accounts earn simple interest based on a minimum monthly balance in the account. For example, if in a single month you had a balance in the account of $900 except for one day, when the balance was $500, then only the $500 is used in calculating the entire month’s worth of interest.
- When Interest Is Deposited. Interest is accumulated and deposited (paid) to the account once monthly, usually on the first day of the month. Thus, the interest earned on your account for the month of January appears as a deposit on February 1.
- Insurance against Loss. Canadian savings accounts at commercial banks are insured by the national Canada Deposit Insurance Corporation (CDIC), which guarantees up to $100,000 in savings. At credit unions, this insurance is usually provided provincially by institutions such as the Deposit Insurance Corporation of Ontario (DICO), which also guarantees up to $100,000. This means that if your bank were to fold, you could not lose your money (so long as your deposit was within the maximum limit). Therefore, savings accounts carry almost no risk.
- Interest Rate Amounts. Interest rates are higher for investments that are riskier. Savings accounts carry virtually no risk, which means the interest rates on savings accounts tend to be among the lowest you can earn. At the time of writing, interest rates on savings accounts ranged from a low of 0.05% to a high of 1.95%. Though this is not much, it is better than nothing and certainly better than losing money!
While a wide range of savings accounts are available, these accounts generally follow one of two common structures when it comes to calculating interest. These structures are flat rate savings accounts and tiered savings accounts. Each of these is discussed separately.
How It Works
Flat-Rate Savings Accounts. A flat-rate savings account has a single interest rate that applies to the entire balance. The interest rate may fluctuate in synch with short-term interest rates in the financial markets.
Follow these steps to calculate the monthly interest for a flat-rate savings account:
Step 1: Identify the interest rate, opening balance, and the monthly transactions in the savings account.
Step 2: Set up a flat-rate table as illustrated here. Create a number of rows equalling the number of monthly transactions (deposits or withdrawals) in the account plus one.
| Dates | Closing Balance in Account | # of Days | Simple Interest Earned |
| I = Prt |
|||
|
Total Monthly |
|||
Step 3: For each row of the table, set up the date ranges for each transaction and calculate the balance in the account for each date range.
Step 4: Calculate the number of days that the closing balance is maintained for each row.
Step 5: Apply Formula 6.1, I = Prt, to each row in the table. Ensure that rate and time are expressed in the same units. Do not round off the resulting interest amounts (I).
Step 6: Sum the Simple Interest Earned column and round off to two decimals.
When you are calculating interest on any type of savings account, pay careful attention to the details on how interest is calculated and any restrictions or conditions on the balance that is eligible to earn the interest.
Example 6.3A: Savings at the Royal Bank
|
The RBC High Interest Savings Account pays 0.75% simple interest on the daily closing balance in the account and the interest is paid on the first day of the following month. On March 1, the opening balance in the account was $2,400. On March 12, a deposit of $1,600 was made. On March 21, a withdrawal of $2,000 was made. Calculate the total simple interest earned for the month of March
|
||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Calculate the total interest amount for the month (I).
|
||||||||||||||||||||||||||
|
What You Already Know Step 1: The following transactions, dates, and interest rate are known: r = 0.75% per year March 1 opening balance = $2,400 March 12 deposit = $1,600 March 21 withdrawal = $2,000
|
How You Will Get There Step 2: Set up a flat-rate table. Step 3: Determine the date ranges for each balance throughout the month and calculate the closing balances. Step 4: For each row of the table, calculate the number of days involved. Step 5: Apply Formula 6.1 to calculate simple interest on each row. Step 6: Sum the Simple Interest Earned column.
|
|||||||||||||||||||||||||
|
||||||||||||||||||||||||||
|
For the month of March, the savings account earned a total simple interest of $1.73, which was deposited to the account on April 1.
|
||||||||||||||||||||||||||
How It Works
Tiered Savings Accounts. A tiered savings account pays higher rates of interest on higher balances in the account. This is very much like a graduated commission on gross earnings, as discussed in Section 4.1. For example, you might earn 0.25% interest on the first $1,000 in your account and 0.35% for balances over $1,000. Most of these tiered savings accounts use a portioning system. This means that if the account has $2,500, the first $1,000 earns the 0.25% interest rate and it is only the portion above the first $1,000 (hence, $1,500) that earns the higher interest rate.
Follow these steps to calculate the monthly interest for a tiered savings account:
Step 1: Identify the interest rate, opening balance, and the monthly transactions in the savings account.
Step 2: Set up a tiered interest rate table as illustrated below. Create a number of rows equalling the number of monthly transactions (deposits or withdrawals) in the account plus one. Adjust the number of columns to suit the number of tiered rates. Fill in the headers for each tiered rate with the balance requirements and interest rate for which the balance is eligible.
| Dates | Closing Balance in Account | # of Days |
Tier Balance Requirements and Interest |
Tier Balance Requirements and Interest |
Tier Balance Requirements and Interest |
|
Eligible I = Prt |
Eligible I = Prt |
Eligible I = Prt |
|||
| Total Monthly Interest Earned | |||||
Step 3: For each row of the table, set up the date ranges for each transaction and calculate the balance in the account for each date range.
Step 4: For each row, calculate the number of days that the closing balance is maintained.
Step 5: Assign the closing balance to the different tiers, paying attention to whether portioning is being used. In each cell with a balance, apply Formula 6.1, where I = Prt. Ensure that rate and time are expressed in the same units. Do not round off the resulting interest amounts (I).
Step 6: To calculate the Total Monthly Interest Earned, sum all interest earned amounts from all tier columns and round off to two decimals.
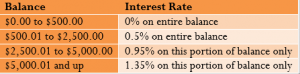
Example 6.3B: A Rate Builder Tiered Account
The Rate Builder savings account at your local credit union pays simple interest on the daily closing balance as indicated in the table below:
|
In the month of August, the opening balance on an account was $2,150.00. Deposits were made to the account on August 5 and August 15 in the amounts of $3,850.00 and $3,500.00. Withdrawals were made from the account on August 12 and August 29 in the amounts of $5,750.00 and $3,000.00. Calculate the simple interest earned for the month of August.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Calculate the total interest amount for the month of August (I).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
What You Already Know Step 1: The interest rate structure is in the table above. The transactions and dates are also known: August 1 opening balance = $2,150.00 August 5 deposit = $3,850.00 August 12 withdrawal = $5,750.00 August 15 deposit = $3,500.00 August 29 withdrawal = $3,000.00
|
How You Will Get There Step 2: Set up a tiered interest rate table with four columns for the tiered rates. Step 3: Determine the date ranges for each balance throughout the month and calculate the closing balances. Step 4: Calculate the number of days involved on each row of the table. Step 5: Assign the closing balance to each tier accordingly. Apply Formula 6.1 to any cell containing a balance. Step 6: Total up all of the interest from all cells of the table.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
For the month of August, the tiered savings account earned a total simple interest of $2.04, which was deposited to the account on September 1.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Short-Term Guaranteed Investment Certificates (GICs)
A guaranteed investment certificate (GIC) is an investment that offers a guaranteed rate of interest over a fixed period of time. In many countries around the world, a GIC is often called a time or term deposit. GICs are found mostly at commercial banks, trust companies, and credit unions. Just like savings accounts, they have a very low risk profile and tend to have much lower rates than are available through other investments such as the stock market or bonds. They are also unconditionally guaranteed, much like savings accounts. In this section, you will deal only with short-term GICs, defined as those that have a time frame of less than one year.
The table below summarizes three factors that determine the interest rate on a short-term GIC: principal, time, and redemption privileges.
|
|
Higher |
Lower |
|
Principal |
Large |
Small |
|
Time |
Longer |
Shorter |
|
Redemption |
Nonredeemable |
Redeemable |
Amount of Principal. Typically, a larger principal is able to realize a higher interest rate than a smaller principal.
-
- Time. The length of time that the principal is invested affects the interest rate. Short-term GICs range from 30 days to 364 days in length. A longer term usually realizes higher interest rates.
- Redemption Privileges. The two types of GICs are known as redeemable and nonredeemable. A redeemable GIC can be cashed in at any point before the maturity date, meaning that you can access your money any time you want it. A nonredeemable GIC “locks in” your money for the agreed-upon term. Accessing that money before the end of the term usually incurs a stiff financial penalty, either on the interest rate or in the form of a financial fee. Nonredeemable GICs carry a higher interest rate.
Example 6.3C: GIC Choices
|
Your parents have $10,000 to invest. They can either deposit the money into a 364-day nonredeemable GIC at Assiniboine Credit Union with a posted rate of 0.75%, or they could put their money into back-to-back 182-day nonredeemable GICs with a posted rate of 0.7%. At the end of the first 182 days, they will reinvest both the principal and interest into the second GIC. The interest rate remains unchanged on the second GIC. Which option should they choose?
|
|
|---|---|
|
For both options, calculate the future value (S), of the investment after 364 days. The one with the higher future value is your parents' better option.
|
|
|
What You Already Know Step 1: For the first GIC investment option: P = $10,000 r = 0.75% per year t = 364 days
For the second GIC investment option: Initial P = $10,000 r = 0.7% per year t = 182 days each
|
How You Will Get There Step 2: The rate is annual, the time is in days. Convert the time to an annual number. Step 3 (1st GIC option): Calculate the maturity value (S1) of the first GIC option after its 364-day term by applying Formula 6.2. Step 3 (2nd GIC option, 1st GIC): Calculate the maturity value (S2) after the first 182-day term by applying Formula 6.2. Step 3 (2nd GIC option, 2nd GIC): Reinvest the first maturity value as principal for another term of 182 days applying Formula 6.2 and calculate the final future value (S3).
|
|
The 364-day GIC results in a maturity value of $10,074.79, while the two back-to-back 182-day GICs result in a maturity value of $10,069.93. Clearly, the 364-day GIC is the better option as it will earn $4.86 more in simple interest.
|
|
Exercises
Mechanics
- A savings account at your local credit union holds a balance of $5,894 for the entire month of September. The posted simple interest rate is 1.35%. Calculate the amount of interest earned for the month (30 days).
- If you place $25,500 into an 80-day short-term GIC at TD Canada Trust earning 0.55% simple interest, how much will you receive when the investment matures?
- In November, the opening balance on a savings account was $12,345. A deposit of $3,000 was made to the account on November 19, and a withdrawal of $3,345 was made from the account on November 8. If simple interest is paid at 0.95% based on the daily closing balance, how much interest for the month of November is deposited to the account on December 1?
- A 320-day short-term GIC earns 0.78% simple interest. If $4,500 is invested into the GIC, what is the maturity value and how much interest is earned?
Applications
- In February of a leap year, the opening balance on your savings account was $3,553. You made two deposits of $2,000 each on February 5 and February 21. You made a withdrawal of $3,500 on February 10, and another withdrawal of $750 on February 17. If simple interest is calculated on the daily closing balance at a rate of 1.45%, how much interest do you earn for the month of February?
- An investor places $30,500 into a short-term 120-day GIC at the Bank of Montreal earning 0.5% simple interest. The maturity value is then rolled into another short-term 181-day GIC earning 0.57% simple interest. Calculate the final maturity value.
- The Mennonite Savings and Credit Union posts the following rate structure for its Daily Interest Savings Account. The entire balance is subject to the highest posted rate, and interest is calculated daily based on the closing balance.
| Balance | Interest Rate |
| $0–$10,000.00 | 0.1% |
| $10,000.01–$25,000.00 | 0.21% |
| $25,000.01–$50,000.00 | 0.34% |
| $50,000.01–$100,000.00 | 0.85% |
| $100,000.01 and up |
1.02% |
The opening balance in February of a non–leap year was $47,335. The transactions on this account were a deposit of $60,000 on February 8, a withdrawal of $86,000 on February 15, and a deposit of $34,000 on February 24. What interest for the month of February will be deposited to the account on March 1?
- An investor with $75,000 is weighing options between a 200-day GIC or two back-to-back 100-day GICs. The 200-day GIC has a posted simple interest rate of 1.4%. The 100-day GICs have a posted simple interest rate of 1.35%. The maturity value of the first 100-day GIC would be reinvested in the second 100-day GIC (assume the same interest rate upon renewal). Which alternative is best and by how much?
- Canadian Western Bank offers a Summit Savings Account with posted interest rates as indicated in the table below. Only each tier is subject to the posted rate, and interest is calculated daily based on the closing balance.
| Balance | Interest Rate |
| $0–$5,000.00 | 0% |
| $5,000.01–$1,000,000.00 | 1.05% |
| $1,000,000.01 and up |
0.80% |
December’s opening balance was $550,000. Two deposits in the amount of $600,000 each were made on December 3 and December 21. Two withdrawals in the amount of $400,000 and $300,000 were made on December 13 and December 24, respectively. What interest for the month of December will be deposited to the account on January 1?
- Sun Life Financial Trust offers a 360-day short-term GIC at 0.65%. It also offers a 120-day short-term GIC at 0.58%. You are considering either the 360-day GIC or three consecutive 120-day GICs. For the 120-day GICs, the entire maturity value would be “rolled over” into the next GIC. Assume that the posted rate increases by 0.1% upon each renewal. If you have $115,000 to invest, which option should you pursue and how much more interest will it earn?
Challenge, Critical Thinking, & Other Applications
- The Regular Savings Account at Steinbach Credit Union posts the following tiered rate structure. Interest is calculated on the entire balance for any given tier.
| Balance | Interest Rate |
| $0–$100,000.00 | 1.75% |
| $100,000.01–$250,000.00 | 1.85% |
| $250,000.01 and up |
1.95% |
For any given month, simple interest is calculated on the lowest monthly closing balance, but the interest is not deposited until January 1 of the following year. On January 1, 2014, the opening balance on an account was $75,000. The following transactions took place throughout the year:
| Date | Activity | Amount |
| February 14 |
Deposit | $133,000 |
| March 30 |
Deposit | $42,000 |
| June 15 |
Withdrawal | $110,000 |
| August 1 |
Deposit | $212,000 |
| October 29 |
Withdrawal | $300,000 |
Calculate the annual amount of interest earned on this account that will be deposited on January 1, 2015.
Interest rates can fluctuate throughout the year. Working with the information from question 11, recalculate the annual amount of interest if all of the posted interest rates were adjusted as follows throughout the year:
-
Effective
DateChange Percent March
1Increase 0.1% July
1Decrease 0.15% September
1Increase 0.25% November
1Decrease 0.05%
13. Interest rates in the GIC markets are always fluctuating because of changes in the short-term financial markets. If you have $50,000 to invest today, you could place the money into a 180-day GIC at Canada Life earning a fixed rate of 0.4%, or you could take two consecutive 90-day GICs. The current posted fixed rate on 90-day GICs at Canada Life is 0.3%. Trends in the short-term financial markets suggest that within the next 90 days short-term GIC rates will be rising. What does the short-term 90-day rate need to be 90 days from now to arrive at the same maturity value as the 180-day GIC? Assume that the entire maturity value of the first 90-day GIC would be reinvested.
14. A Citibank Savings Account posts the following simple interest rate structure. All interest is paid on entire balances, and interest is deposited to the account every quarter.
| Balance | Interest Rate |
| $0–$2,500.00 | 0.05% |
| $2,500.01–$5,000.00 | 0.1% |
| $5,000.01 and up |
0.75% |
On January 1, 2013, the opening balance was $3,300. The following transactions took place during the first quarter (January 1 to March 31):
| Deposits | Withdrawals | |||
| January 4 |
$350 | January 15 | $500 | |
| January 29 |
$1,800 | January 19 | $1,000 | |
| February 7 |
$2,300 | February 20 | $1,300 | |
| March 2 |
$2,400 | March 7 | $4,000 | |
| March 22 |
$1,100 | March 25 | $2,000 | |
Calculate the total amount of interest that will be deposited to the account on April 1, 2013.
- You are considering the following short-term GIC investment options for an amount of $90,000.
| Option 1 |
Option 2 |
Option 3 |
Option 4 |
|
| Institution | Coast Capital Savings | MCAN Mortgage Corp. | DUCA Financial Services | Sun Life Financial Trust |
| Term | 360 day | 2 × 180 day | 3 × 120 day | 4 × 90 day |
| Posted Rate |
0.8% | 0.75% | 0.72% | 0.715% |
In all cases, assume that the posted rates remain unchanged and that the entire maturity value will be reinvested in the next short-term GIC. Calculate the total maturity value for each option at the end of 360 days.
The Language of Business Mathematics
accrued interest Any interest amount that has been calculated but not yet placed (charged or earned) into an account.
commercial paper A short-term financial instrument with maturity no longer than one year that is issued by large corporations.
compound interest A system for calculating interest that primarily applies to long-term financial transactions with a time frame of one year or more; interest is periodically converted to principal throughout a transaction, with the result that the interest itself also accumulates interest.
current balance The balance in an account plus any accrued interest.
demand loan A short-term loan that generally has no specific maturity date, may be paid at any time without any interest penalty, and where the lender may demand repayment at any time.
discount rate An interest rate used to remove interest from a future value.
equivalent payments Two payments that have the same value on the same day factoring in a fair interest rate.
face value of a T-bill The maturity value of a T-bill, which ispayable at the end of the term. It includes both the principal and interest together.
fixed interest rate An interest rate that is unchanged for the duration of the transaction.
future value The amount of principal with interest at a future point of time for a financial transaction. If this future point is the same as the end date of the financial transaction, it is also called the maturity value.
guaranteed investment certificate (GIC) An investment that offers a guaranteed rate of interest over a fixed period of time.
interest amount The dollar amount of interest that is paid or earned.
interest rate The rate of interest that is charged or earned during a specified time period.
legal due date of a note Three days after the term specified in an interest-bearing promissory note is the date when a promissory note becomes legally due. This grace period allows the borrower to repay the note without penalty in the event that the due date falls on a statutory holiday or weekend.
maturity date The date upon which a transaction, such as a promissory note, comes to an end and needs to be repaid.
maturity value The amount of money at the end of a transaction, which includes both the interest and the principal together.
present value The amount of money at the beginning of a time period in a transaction. If this is in fact the amount at the start of the financial transaction, it is also called the principal. Or it can simply be the amount at some time earlier before the future value was known. In any case, the amount excludes the interest.
prime rate An interest rate set by the Bank of Canada that usually forms the lowest lending rate for the most secure loans.
principal The original amount of money that is borrowed or invested in a financial transaction.
proceeds The amount of money received from a sale.
promissory note An unconditional promise in writing made by one person to another person to pay a sum of money on demand or at a fixed or determinable future time.
repayment schedule A table that details the financial transactions in an account, including the balance, interest amounts, and payments.
savings account A deposit account that bears interest and has no stated maturity date.
secured loan Those loans that are guaranteed by an asset such as a building or a vehicle that can be seized to pay the debt in case of default.
simple interest A system for calculating interest that primarily applies to short-term financial transactions with a time frame of less than one year.
student loan A special type of loan designed to help students pay for the costs of tuition, books, and living expenses while pursuing postsecondary education.
time period The length of the financial transaction for which interest is charged or earned. It may also be called the term.
treasury bills Short-term financial instruments with maturities no longer than one year that are issued by both federal and provincial governments.
unsecured loan Those loans backed up by the general goodwill and nature of the borrower.
variable interest rate An interest rate that is open to fluctuations over the duration of a transaction.
yield The percentage increase between the sale price and redemption price on an investment such as a T-bill or commercial paper.
The Formulas You Need to Know
Symbols Used
S = maturity value or future value in dollars
I = interest amount in dollars
P = principal or present value in dollars
r = interest rate (in decimal format)
t = time or term
Formulas Introduced
Formula 6.1 Simple Interest: I = Prt (Section 6.1)
Formula 6.2 Simple Interest for Single Payments: S = P(1 + rt) (Section 6.2)
Formula 6.3 Interest Amount for Single Payments: I = S − P (Section 6.2)
Technology
Calculator
The following calculator functions were introduced in this chapter:
Date Function
 2nd Profit to access.
2nd Profit to access.- Enter two of the three variables (DT1, DT2, DBD) by pressing Enter after each input and using and to scroll through the display. The variables are:
- DT1 = The starting date of the transaction
- DT2 = The ending date of the transaction
- DBD = The days between the dates, counting the first day but not the last, which is the time period of the transaction.
- ACT / 360 = A setting for determining how the calculator determines the DBD. In Canada, you should maintain this setting on ACT, which is the actual number of days. In other countries, such as the United States, they treat each year as having 360 days (the 360 setting) and each month as having 30 days. If you need to toggle this setting, press 2nd SET.
- Enter all dates in the format of MM.DDYY, where MM is the numerical month, DD is the day, and YY is the last two digits of the year. DD and YY must always be entered with both digits.
- Press CPT on the unknown (when it is on the screen display) to compute the answer.
 Chapter 8 Review Exercises
Chapter 8 Review Exercises
Mechanics
- If $4,000 is borrowed from April 3 to June 22 at a simple interest rate of 3.8%, how much interest is paid on the loan?
- A savings account pays flat-rate interest of 1.45%. If a balance of $3,285.40 is maintained for the entire month of August, how much interest does the savings account earn?
- What is the legal due date and maturity value on that date for a 125-day $51,000 promissory note issued on May 14 at
- A full-time student graduated from college on December 16, 2013, with $26,500 in outstanding student loans. Calculate the interest accrued during his grace period if the prime rate is 4.7%.
- A 182-day $1,000,000 Government of British Columbia T-bill was issued when the market rate of return was 4.21%. Calculate the purchase price of the T-bill on its issue date.
- If you place $8,000 into a 300-day short-term GIC at Scotiabank earning 0.95% simple interest, how much will you receive when the investment matures?
Applications
- Proper accounting procedures require accountants to separate principal and interest components on any loan. Allocate the principal and interest portions of a $24,159.18 payment clearing a 147-day loan at 8.88%.
- Cadillac Fairview withdrew $115,000 from its operating loan account on September 4 to perform some needed maintenance on one of its properties. The operating loan requires interest at prime + 3% and fixed $25,000 monthly payments starting October 1. The company thinks it can make an additional payment of $35,000 on November 18. The prime rate on the date of withdrawal was 3.6%, and it increased by 0.5% on October 27. Construct a full repayment schedule for this loan.
- As part of your financial plan for retirement, you purchased a 270-day $25,000 commercial paper on its date of issue, July 14, when market yields were 2.94%. 234 days later, you sold the note when market yields were 2.76%. What rate of return did you realize on your investment?
- Alterna Savings and Bank offers a Daily Interest Savings Account with posted interest rates as indicated in the table below. The entire balance qualifies for the posted rate, and interest is calculated daily based on the closing balance.
|
Balance |
Interest Rate |
|
$0–$5,000.00 |
0.10% |
|
$5,000.01–$10,000.00 |
0.15% |
|
$10,000.01–$25,000.00 |
0.20% |
|
$25,000.01 and up |
0.25% |
BOS Designer Candles Inc. has an opening balance in July of $17,500. Three deposits in the amounts of $6,000, $4,000, and $1,500 were made on July 4, July 18, and July 22, respectively. Two withdrawals in the amount of $20,000 and $8,000 were made on July 20 and July 27, respectively. What interest for the month of July will Alterna deposit to the account on August 1?
- Shannon has a $68,000 student loan when she graduates on August 28, 2014, and the prime rate is set at 4.9%. She will convert the interest to principal at the end of her grace period, and she elects to take the variable rate on her student loan. She sets her fixed monthly payment at $1,400. The prime rate decreases by 0.5% on January 15 and rises by 0.75% on April 25. Compute the first six repayments of her repayment schedule. Calculate the total interest charged for both the grace period and the six payments combined.
- Sturm put $48,700 into a 10-month term deposit, but needed to withdraw the funds after five months to deal with a family emergency. The credit union penalized him 2.35% off of his interest rate for the early withdrawal and deposited $49,602.98 into his account.
- What was Sturm’s original interest rate?
- How much interest, in dollars, was he penalized for the early withdrawal?
- Jerry’s Concrete allows his customers to create six-month promissory notes on any stamped concrete driveway project with interest at 8.9%. Three months after completing a $17,300 job on March 2, 2014, Jerry had some liquidity problems and sold the promissory note to a financial institution at an interest rate of 10.35%. Calculate Jerry’s proceeds on the sale.
- Three hundred days from now you will be departing on a backpacking trip through Europe. You need $4,000 in spending money to take with you. Today, you currently have saved $3,960.
- If you place your money in consecutive 100-day short-term GICs earning 1.02%, will you meet your goal? Assume the full maturity values are reinvested into the next GIC.
- What would the interest rate need to be if you had placed your money into a single 300-day short-term GIC to reach your goal?
Challenge, Critical Thinking, & Other Applications
- A credit union posts the following tiered interest rate structure for its savings accounts. Only each tier is subject to the posted rate and is computed using the daily opening balance in the account. Interest is deposited to the account on the last day of every month.
|
Balance |
Interest Rate |
|
$0–$4,000.00 |
0.15% |
|
$4,000.01–$8,000.00 |
0.25% |
|
$8,000.01 and up |
0.45% |
On August 1, the opening balance was $6,400. Three deposits of $2,000, $3,500, and $1,500 were made on August 3, August 10, and August 27, respectively. Two withdrawals of $7,000 and $1,900 were made on August 6 and August 21, respectively. Compute the total interest earned for the month of August.
- Island Lakes Dental (ILD) found itself with an urgent need to replace its X-ray machine when its existing machine suddenly became inoperable. It borrowed $43,000 on May 12 from its operating loan with interest set at prime + 2.4%. The prime rate was 2.75% and increased by 0.5% on June 5. The loan requires payment of the balance in full when the balance is less than $5,000, or 10% of the current balance on the first of every month. ILD made payments of $15,000 on May 29 and $21,000 on June 21. Create a full repayment schedule for its operating loan and calculate the total interest charged on the purchase.
- Pendragon Inc. has an operating loan with a balance of $52,000 on September 1 with interest set at prime + 4.75%. On the first of every month the operating loan requires repayment of the accrued interest only. The current prime rate is 4.75% and will decrease to 4.25% on October 7. On September 15, it has a 270-day $20,000 GIC with 3.8% interest maturing. On October 15, it has a 320-day $18,000 GIC with 3.68% interest maturing. It will use these maturing investments to pay down its operating loan. Construct a repayment schedule from September 1 to November 1 only.
- A 364-day, $50,000 face value T-bill is issued when market yields are 2.85%. The T-bill is sold to another investor every 91 days until maturity, with yields of 3.1%, 2.98%, and 3.15% on each of the dates of sale, respectively. Compute the purchase price for each investor, including the date of issue. For each investor, calculate the actual rate of return realized on their investment.
- Brant and Sylvia have a prime + 2.35% HELOC with a $30,000 balance on March 1 with accrued interest payable on the first of every month. They also have a savings account with a $10,000 balance on March 1 earning 0.85% payable on the first of every month. On March 18 they deposited $4,000 into the savings account. On both March 5 and March 30 they transferred $3,000 from their savings to their HELOC. Prime was initially at 3.75% but increased to 4.25% on March 22. Calculate the balance on April 1 in both the savings account and the HELOC.
- Norbert is looking to make a short-term investment for 120 days with the $25,000 he just inherited from his father’s estate. His options are as follows. Compute the maturity values of each of the options and rank his choices.
- Two back-to-back 60-day GICs earning 2.25% today, with a forecasted rate of 2.5% 60 days from now. Assume the full maturity value is rolled over into the next investment.
- One 120-day GIC earning 2.35%.
- A 90-day $25,000 face value T-bill earning 2.28% followed by a 30-day $25,000 face value T-bill earning a projected 2.38%. Assume any leftover funds are invested to earn 0.85% interest.
Chapter 6 Case Study
Managing A Company’s Investments
The Situation
As with most mid-size to large companies, Lightning Wholesale has a finance department to manage its money. The structure of Lightning Wholesale’s financial plan allows each department to have its own bank account from which all expenses, purchases, and charges are deducted. This same account has all revenues and interest deposited into it.
The manager of the sporting goods department wants a summary of all interest amounts earned or charged to her department for the year 2013. This will allow her to better understand and assess the financial policies of the company and make any necessary changes for 2014.

The Data
|
Month |
Total Sales Revenue |
Cost of Goods Sold |
Operating Expenses |
|
January |
$1,798 |
$2,102 |
$156 |
|
February |
$2,407 |
$2,242 |
$100 |
|
March |
$2,568 |
$2,606 |
$222 |
|
April |
$2,985 |
$2,719 |
$258 |
|
May |
$3,114 |
$2,831 |
$269 |
|
June |
$3,242 |
$2,887 |
$280 |
|
July |
$3,306 |
$3,363 |
$286 |
|
August |
$3,852 |
$4,203 |
$333 |
|
September |
$4,815 |
$6,306 |
$525 |
|
October |
$7,222 |
$11,210 |
$625 |
|
November |
$12,839 |
$8,408 |
$1,111 |
|
December |
$9,630 |
$1,569 |
$833 |
(All numbers in thousands of dollars)
Important Information
- The balance in the sporting goods bank account on December 31, 2012, was $2,245,636.45.
- The bank account permits a negative balance, which the bank treats as an operating loan. The interest rate on any operating loan is prime + 0.5%. Accrued interest is placed into the account on the last day of each month.
- When a positive balance exists, the bank pays interest at 0.85% on the first $50,000 in the account and 1.2% only on the portion above $50,000. Interest is deposited on the last day of each month.
- On the last day of each month, the finance department purchases T-bills in the market that will mature by the last day of the next month. The face value of T-bills are bought in denominations of exactly $100,000 in a quantity as permitted by the current balance in the bank account. If the bank account has a negative balance (i.e., it is using its operating loan), no T-bills are purchased that month. For example, if the bank account has a balance of $350,000 on March 31, three $100,000 T-bills will be purchased with 30 days left to maturity.
- Assume all revenues are deposited to the account at the end of the corresponding month.
- Assume all cost of goods sold and operating expenses are deducted at the end of the corresponding month.
- For simplicity, assume the balance in the bank account remains unchanged throughout each month.
Your Tasks
The manager wants a report that summarizes the following information from December 31, 2012, to December 31, 2013:
- The total interest earned through T-bill investments.
- The total interest earned from the bank account.
- The total interest charged by any operating loans.
- The final balance in the bank account as of December 31, 2013, when no purchases of T-bills for January 2014 have been made.
In order to meet the manager’s requirements, work through 2013 month by month starting from December 31, 2012, by following the steps below. Once arriving at December 31, 2013, use the answers to provide the four pieces of information requested by the manager.
- Using the opening balance, determine the face value of T-bills that can be purchased. If the balance is negative, no T-bills are purchased, so skip to step 4.
- Calculate the purchase price of the T-bills using the current market yield and the number of days until the end of the next month. The difference between the purchase price and the face value is the total interest earned for the month by T-bills.
- Deduct the purchase price of the T-bills from the balance in the account.
- Examine the account balance.
- If the balance is positive, calculate the interest earned for the month based on the tiered interest rate structure. This is the total interest earned by the investment for the month.
- If the balance is negative, charge interest to the account for the month using the interest rate charged by the bank. This is the total interest charged by the operating loan for the month.
- To figure out the balance at the end of the next month, take the balance from step 4, add the face value of the T-bills that are maturing at the end of the month, add any interest earned from the bank account (step 4a), deduct any interest charged on the operating loan (step 4b), add the revenues for the month, and deduct the expenses and cost of goods sold for the month.
- Go back to step 1 and repeat for the next month.
- When all months are complete, calculate the required totals and present the requested summary information to the manager.
|
Creative |
8- |