Marketing Applications

OER Lab

4 Marketing Applications

Chapter 4 Topics

4.1 Discounts

4.2 Markup

4.3 Markdown

4.4 Merchandising

When you buy an iPod, it is very important that the right price is set. The price should:

be seen as fair by you the buyer,
pay for the costs (plastics, battery, buttons, circuit boards, headset) and expenses (employees, factory, electricity, distribution) of making the iPod, and
allow the seller’s business to make some extra money as profit so that it can grow its business further.

If your business is selling a product, you will need to pay close attention to price adjustments because they affect profitability. Various discounts, like putting items on sale, may increase sales while lowering the amount of profit per transaction. How do you know where to set the balance to maximize profit overall?

As a student in a business program, consider this chapter essential to the success of any business. Whether your pricing strategy is high or low, the company must ensure that it can still pay its bills as a minimum requirement. And that requires careful juggling of many factors. If it fails to manage its pricing properly, the company will go bankrupt!

This chapter will make you a smarter business professional and a wiser consumer. You shop retail almost every day and regularly purchase goods and services. If you understand how product pricing works, you can make sense of “deals.” You can easily explain why the same product sells for two different prices at two different stores.

In this chapter, you must learn the language of marketers to perform merchandising mathematics involving product costs, expenses, prices, markups, markdowns, and ultimately profitability. Once the study of the various pricing components is complete, we will see how the various pieces of the pricing puzzle fit together into a cohesive merchandising environment.

4.1 Discounts

You mutter in exasperation, “Why can’t they just set one price and stick with it?” Your mind boggles at all the competing discounts you encounter at the mall in your search for that perfect Batman toy for your nephew. Walmart is running their Rollback promotion and is offering a Batmobile for 25% off, regularly priced at $49.99. Toys R’ Us has an outlet in the parking lot where the regular price for the same toy is $59.99, but all Batman products are being cleared out at 40% off. You head over to The Bay for a warehouse clearance event that has the same toy priced at $64.99 but at 35% off. It is also Bay Days, which means you can scratch and win a further 10% to 20% off the sale price. You go to Dairy Queen for a Blizzard to soothe your headache while you figure things out.

The cost of a product is the amount of money required to obtain the merchandise. If you are a consumer, the ticketed price tag on the product is your cost. If you are a reseller (also known as a middleman or intermediary), what you pay to your supplier for the product is your cost. If you are a manufacturer, then your cost equals all of the labour, materials, and production expenditures that went into creating the product.

A discount is a reduction in the price of a product. As a consumer, you are bombarded with discounts all the time. Retailers use various terms for discounts, including sales or clearance. If your business purchases a product from a supplier, any discount it receives lowers how much the business pays to acquire the product. When a business buys products, the price paid is the cost to the business. Therefore, a lower price means a lower cost.

If your business is the one selling the product, any discount offered lowers the selling price and reduces revenue per sale. Since the revenue must cover all costs and expenses associated with the product, the lower price means that the business reduces profits per sale. In business, it is common practice to express a discount as a percentage off the regular price.

How Distribution and Pricing Work

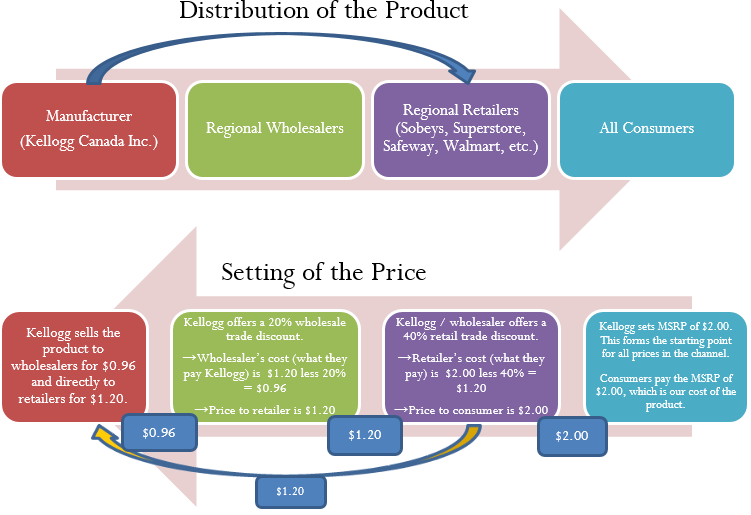
Start with distribution in the top half of the figure and work left to right. As an example, let’s look at a manufacturer such as Kellogg Canada Inc. (which makes such products as Pop-Tarts, Eggo Waffles, and Rice Krispies). Kellogg’s Canadian production plant is located in London, Ontario. To distribute its products to the rest of Canada, Kellogg Canada uses various regional wholesalers. Each wholesaler then resells the product to retailers in its local trade area; however, some retailers (such as the Real Canadian Superstore) are very large, and Kellogg Canada distributes directly to these organizations, bypassing the wholesaler as represented by the blue arrow. Finally, consumers shop at these retailers and acquire Kellogg products.

The relationship of distribution to pricing is illustrated in the bottom half of the figure, working right to left. For now, focus on understanding how pricing works; the mathematics used in the figure will be explained later in this chapter. Kellogg Canada sets a manufacturer’s suggested retail price, known as the MSRP. This is a recommended retail price based on consumer market research. Since grocery retailers commonly carry thousands or tens of thousands of products, the MSRP helps the retailer to determine the retail price at which the product should be listed. In this case, assume a $2.00 MSRP, which is the price consumers will pay for the product.

The retailer must pay something less than $2.00 to make money when selling the product. Kellogg Canada understands its distributors and calculates that to be profitable most retailers must pay approximately 40% less than the MSRP. Therefore, it offers a 40% discount. If the retailer purchases directly from Kellogg, as illustrated by the yellow arrow, the price paid by the retailer to acquire the product is $2.00 less 40%, or $1.20. Smaller retailers acquire the product from a wholesaler for the same price. Thus, the retailer’s cost equals the wholesaler’s price (or Kellogg Canada’s price if the retailer purchases it directly from Kellogg).

The wholesaler’s price is $1.20. Again, Kellogg Canada, knowing that the wholesaler must pay something less than $1.20 to be profitable, offers an additional 20% discount exclusively to the wholesaler. So the price paid by the wholesaler to acquire the product from Kellogg Canada is $1.20 less 20%, or $0.96. This $0.96 forms Kellogg Canada’s price to the wholesaler, which equals the wholesaler’s cost.

In summary, this discussion illustrates two key pricing concepts:

Companies higher up in the distribution channel pay lower prices than those farther down the channel. Companies receive discounts off the MSRP based on their level in the distribution system. This may result in multiple discounts, such as a wholesaler receiving both the retailer’s discount and an additional discount for being a wholesaler.
One organization’s price becomes the next organization’s cost (assuming the typical distribution channel structure):
Manufacturer’s Price = Wholesaler’s Cost
Wholesaler’s Price = Retailer’s Cost
Retailer’s Price = Consumer’s Cost

Types of Discounts

You will perform discount calculations more effectively if you understand how and why single pricing discounts and multiple pricing discounts occur. Businesses or consumers are offered numerous types of discounts, of which five of the most common are trade, quantity, loyalty, sale, and seasonal.

Trade Discounts. A trade discount is a discount offered to businesses only based on the type of business and its position in the distribution system (e.g., as a retailer, wholesaler, or any other member of the distribution system that resells the product). Consumers are ineligible for trade discounts. In the discussion of the figure, two trade discounts are offered. The first is a 40% retail trade discount, and the second is a 20% wholesale trade discount. Typically, a business that is higher up in the distribution system receives a combination of these trade discounts. For example, the wholesaler receives both the 40% retail trade discount and the 20% wholesale trade discount from the MSRP. The wholesaler’s cost is calculated as an MSRP of $2.00 less 40% less 20% = $0.96.
Quantity Discounts. A quantity discount (also called a volume discount) is a discount for purchasing larger quantities of a certain product. If you have ever walked down an aisle in a Real Canadian Superstore, you probably noticed many shelf tags that indicate quantity discounts, such as “Buy one product for $2” or “Take two products for $3.” Many Shell gas stations offer a Thirst Buster program in which customers who purchase four Thirst Busters within a three-month period get the fifth one free. If the Thirst Busters are $2.00 each, this is equivalent to buying five drinks for $10.00 less a $2.00 quantity discount.
Loyalty Discounts. A loyalty discount is a discount that a seller gives to a purchaser for repeat business. Usually no time frame is specified; that is, the offer is continually available. As a consumer, you see this regularly in marketing programs such as Air Miles or with credit cards that offer cash back programs. For example, Co-op gas stations in Manitoba track consumer gasoline purchases through a loyalty program and mails an annual loyalty discount cheque to its customers, recently amounting to 12.5¢ per litre purchased. In business-to-business circles, sellers typically reward loyal customers by deducting a loyalty discount percentage, commonly ranging from 1% to 5%, from the selling price.
Sale Discounts. A sale discount is a temporary lowering of the price from a product’s regular selling price. Businesses put items on sale for a variety of reasons, such as selling excess stock or attracting shoppers. You see such promotional events all the time: LED monitors are on sale at Best Buy; Blu-Ray discs are half off at Walmart; The Brick is having a door crasher event Saturday morning.
Seasonal Discounts. A seasonal discount is a discount offered to consumers and businesses for purchasing products out of season. At the business level, manufacturers tend to offer seasonal discounts encouraging retailers, wholesalers, or distributors to purchase products before they are in season. Bombardier Inc. manufactures Ski-Doos, which are sold in Canada from approximately November through March—a time of year when most of the country has snow and consumers would want to buy one. To keep production running smoothly from April through October, Bombardier could offer seasonal discounts to its wholesalers and retailers for the coming winter season. At a retail level, the examples are plentiful. On November 1 most retailers place their Halloween merchandise on seasonal discount to clear out excess inventory, and many retailers use Boxing Day (or Boxing Week) to clear their out-of-season merchandise.

Single Discounts

Let’s start by calculating the cost when only one discount is offered. Later in this section you will learn how to calculate a cost involving multiple discounts.

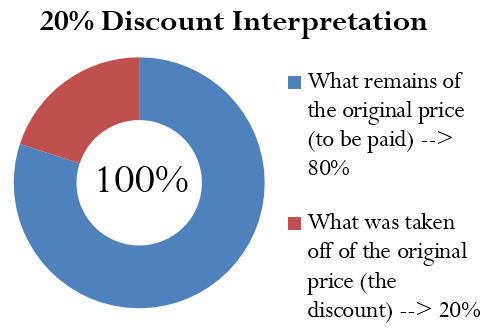
Figuring out the price after applying a single discount is called a net price calculation. When a business calculates the net price of a product, it is interested in what you still have to pay, not in what has been removed. Note in Formula 4.1 below that you take 1 and subtract the discount rate to determine the rate owing. If you are eligible for a 20% discount, then you must pay 80% of the list price, as illustrated in the figure below:

A circle diagram illustrating a 20% discount. The circle represents the total cost of the product (100%). The red section of the circle illustrates the discount, or what was taken off the original price (20%). The remaining blue portion of the circle illustrates what remains to be paid of the original price (80%).

Formula 4.1 – Single Discount

$N= L\times(1-d)$

$N$ is the Net Price: The price of the product after the discount is removed from the list price. It is a dollar amount representing what price remains after you have applied the discount.

$L$ is the List Price: The normal or regular dollar price of the product before any discounts. It is the Manufacturer's Suggested Retail Price (MRSP).

$d$ is the Discount Rate: The percentage (in decimal format) of the list price that is deducted.

Formula 4.1 includes rate, portion, and base, where the list price is the base, the $(1 − d)$ is the rate, and the net price represents the portion of the price to be paid.

Formula 4.2a and Formula 4.2b – Discount Amount

Formula 4.2a

$D\char36=L\times d$

Formula 4.2b

$D\char36=L-N$

$D\char36$ is Discount Amount: Determine the discount amount in one of two ways, depending on what information is known:
If the list price and discount rate are known, apply Formula 4.2a.
If the list price and net price are known, apply Formula 4.2b.

$L$ is List Price: The dollar amount of the price before any discounts.

$N$ is Net Price: The dollar amount of the price after you have deducted all discounts.

$d$ is Discount Rate: The percentage (in decimal format) of the list price to be deducted. This time, you are interested in figuring out the amount of the discount, therefore you do not take it away from 1.

Notice that Formula 4.1 requires the discount to be in a percentage (decimal) format; sometimes a discount is expressed as a dollar amount, though, such as “Save $5 today.” Formulas 4.2a and 4.2b relate the discount dollar amount to the list price, discount percent, and net price. Choose one formula or the other depending on which variables are known.

How It Works

Follow these steps to calculate the net price involving a single discount. These steps are adaptable if the net price is a known variable and one of the other variables is unknown.

Step 1: Identify any known variables, including list price, discount rate, or discount amount.

Step 2: If the list price is known, skip this step. Otherwise, solve for list price using an appropriate formula.

Step 3: Calculate the net price.

If the list price and discount are are known, apply Formula 4.1.
If the list price and discount amount are known, apply Formula 4.2b and rearrange for $N$ .

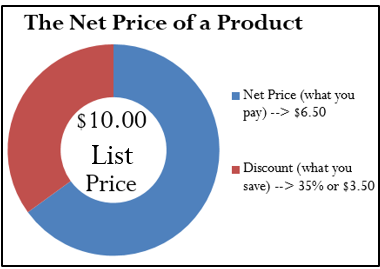
Assume a product sells for $10 and is on sale at 35% off the regular price. Calculate the net price for the product.

Step 1: The list price of the product is $L = \char36 10$ . It is on sale with a discount rate of $d = 0.35$ .

Step 2: List price is known, so this step is not needed.

Step 3: Applying Formula 4.1 results in a new price of

$N=\char36 10\times(1-0.35)= \char36 6.50$ .

Note that if you are interested in learning the discount amount, you apply Formula 4.2b to calculate:

$D\char36 =\char36 10-\char36 6.50=\char36 3.50$ .

A circle diagram illustrating the net price of a product. The circle represents the list price ($10.00). The red portion of the circle represents the discount, or what you save (35% or $3.50.) The blue portion of the circle illustrates the net price, or what you pay ($6.50.)

You can combine Formula 4.1 and either version of Formula 4.2 in a variety of ways to solve any single discount situation for any of the three variables. As you deal with increasingly complicated pricing formulas, your algebraic skills in solving linear equations and substitution become very important.

Many of the pricing problems take multiple steps that combine various formulas, so you need to apply the PUPP model systematically. In any pricing problem, you must understand which variables are provided and match them up to the known formulas. To get to your end goal, you must look for formulas in which you know all but one variable. In these cases, solving for variables will move you forward toward solving the overall pricing problem.

If you find you cannot produce a formula with only one unknown variable, can you find two formulas with the same two unknowns? If so, recall from Chapter 1 that you can use your algebraic skills to find the roots of the two equations simultaneously. Alternatively, you can solve one formula for a variable then substitute it into the other formula, allowing you to isolate the remaining variable. Throughout the examples in this chapter you will see many applications of these algebraic skills.

Remember to apply the rounding rules:

1. Until you arrive at the final solution, avoid rounding any interim numbers unless you have some special reason to do so.
2. Round all dollar amounts to the nearest cent. If the dollar amount has no cents, you may write it either without the cents or with the “.00” at the end.
3. Round all percentages to four decimals when in percent format.

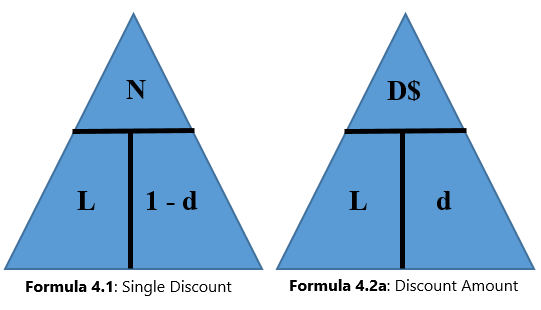
When working with single discounts, you are not always solving for the net price. Sometimes you must calculate the discount percent or the list price. At other times you know information about the discount amount but need to solve for list price, net price, or the discount rate. The triangle technique can remind you how to rearrange the formulas for each variable, as illustrated in the figure below.

Give It Some Thought:

Will you pay more than, less than, or exactly $10.00 for a product if you are told that you are paying:
a. a net price of $10.00 when there is a discount of 25%?
b. a list price of $10.00 when there is a discount of 25%?
If an item is subject to a 40% discount, will the net price be more than or less than half of the list price of the product?

Example 4.1A – Determining the Retailer’s Net Price for a Pair of Jeans

A manufacturer that sells jeans directly to its retailers uses market research to find out it needs to offer a 25% trade discount. In doing so, the retailers will then be able to price the product at the MSRP of $59.99. What price should retailers pay for the jeans?

Plan:
Calculate how much a retailer should pay for the jeans after the regular price has been discounted to accommodate the trade discount. This is called the net price for the product, or $N$ .

Understand:
Step 1: The list price and the discount rate are known.

$L= \char36 59.99$
$d = 0.25$

Step 2: List price is known, so skip this step.

Step 3: Apply Formula 4.1

Perform:
Step 3:

$N=\char36 59.99\times(1-0.25)=\char36 59.99\times0.75=\char36 44.99$

Present:
The manufacturer should sell the jeans to the retailers for $44.99.

Example 4.1B – Determining the List Price of a Jacket

Winners pays a net price of $27.50 for a winter jacket after receiving a retail trade discount of 45%. What was the MSRP of the jacket?

Plan:
Calculate the MSRP for the jacket before Winners received the retail trade discount to arrive at the net price. This is called the list price for the product, or $L$ .

Understand:
Step 1: The net price and the discount rate are known:

$N = \char36 27.50$
$d = 0.45$

Step 2: List price is the unknown variable; skip this step.

Step 3: Apply Formula 4.1, rearranging for L.

Perform:
Step 3:

$\begin{array}{r} \char36 27.50=L(1-0.45)\\ L=\char36 27.50\div(1-0.45)\\ L=\char36 27.50\div0.55=\char36 50.00 \end{array}$

Present:
The MSRP, or list price, of the winter jacket is $50.00.

Example 4.1C – Determining the Discount Percent and Discount Amount

You are shopping at Mountain Equipment Co-op for a new environmentally friendly water bottle. The price tag reads $14.75, which is $10.24 off the regular price. Determine the discount rate applied.

Plan:
You need to find out how the sale price translates into the discount rate, or $d$ .

Understand:
Step 1: The discount amount and net price are known:

$D\char36 = \char36 10.24$
$N = \char36 14.75$

Step 2: Use Formula 4.2b to calculate the list price, rearranging for $L$ .

Step 3: Convert the discount amount into a percentage by applying Formula 4.2a, rearranging for $d$ .

Perform:
Step 2:
List price:

$\begin{array}{r} \char36 10.24=L-\char36 14.75\\ L = \char36 24.99 \end{array}$

Step 3:
Discount rate:

$d=D\char36\div L$

$\begin{array}{r} d=\frac{\char36 10.24}{\char36 24.99}=0.409764&{\textrm{ or }}&40.9764\% \end{array}$

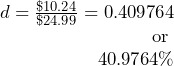
Present:
The water bottle today has been reduced in price by the amount of $10.24. This represents a sale discount of 40.9674%.

Multiple Discounts

You are driving down the street when you see a large sign at Old Navy that says, “Big sale, take an additional 25% off already reduced prices!” In other words, products on sale (the first discount) are being reduced by an additional 25% (the second discount). Because Formula 4.1 handles only a single discount, you must use an extended formula in this case.

Businesses commonly receive more than one discount when they make a purchase. Consider a transaction in which a business receives a 30% trade discount as well as a 10% volume discount. First, you have to understand that this is not a 30% + 10% = 40% discount. The second discount is always applied to the net price after the first discount is applied. Therefore, the second discount has a smaller base upon which it is calculated. If there are more than two discounts, you deduct each subsequent discount from continually smaller bases. Formula 4.3 expresses how to calculate the net price when multiple discounts apply.

Formula 4.3 – Multiple Discounts

$N=L\times(1-d_1)\times(1-d_2)\times\cdots\times(1-d_n)$

$N$ is Net Price: The dollar amount of the price after all discounts have been deducted.
$L$ is List Price: The dollar amount of the price before any discounts.
$d_1$ is First Discount, $d_2$ is Second Discount, $d_n$ is nth Discount:
When there is more than one discount, you must extend beyond Formula 4.1 by multiplying another discount expression. These discounts are represented by the same d symbol; however, each discount receives a subscript to make its symbol unique. Therefore, the first discount receives the symbol of $d_1$ , the second discount receives the symbol $d_2$ , and so on. Recall that the symbol $n$ represents the number of pieces of data (a count), so you can expand or contract this formula to the exact number of discounts being offered.

It is often difficult to understand exactly how much of a discount is being received when multiple discounts are involved. Often it is convenient to summarize the multiple discount percentages into a single percentage. This makes it easier to calculate the net price and aids in understanding the discount benefit. Simplifying multiple percent discounts into a single percent discount is called finding the single equivalent discount. Whether you apply the multiple discounts or just the single equivalent discount, you arrive at the same net price. The conversion of multiple discount percentages into a single equivalent discount percent is illustrated in Formula 4.4.

Formula 4.4 – Single Equivalent Discount

$d_e_q_u_i_v=1-(1-d_1)\times(1-d_2)\times\cdots\times(1-d_n)$

$d_e_q_u_i_v$ (or just $d$ ) is the single equivalent discount rate that is equal to the series of multiple discounts. Recall that taking $(1-d)$ calculates what you pay. Therefore, if you take 1, which represents the entire amount, and reduce it by what you pay, the rate left over must be what you did not pay. In other words, it is the discount rate.

$d_1$ is First Discount, $d_2$ is Second Discount, $d_n$ is nth Discount:
This is the same notation as in Formula 4.3. Since there are multiple discounts, each discount receives a numerical subscript to give it a unique identifier. You can expand or contract the formula to the exact number of discounts being offered.

How It Works

Refer back to the steps in calculating net price. The procedure for calculating a net price involving a single discount extends to a more generic procedure involving multiple discounts. As with the single discount procedures, you can adapt the model if the net price is known and one of the other variables is unknown. Follow these steps to calculate the net price involving any number of discounts:

Step 1: Identify any known variables, including list price, discount rate(s), or discount amount.

Step 2: If the list price is known, skip this step. Otherwise, solve for list price.

If only one discount is involved, apply Formula 4.2a.
If more than one discount is involved, the discount amount represents the total discount amount received from all of the discounts combined. This requires you first to convert the multiple discount rates into an equivalent single discount rate using Formula 4.4 and then to apply Formula 4.2a.

Step 3: Calculate the net price.

If the list price and only a single known discount rate are involved, apply Formula 4.1.
If the list price and multiple discount rates are known and involved, apply Formula 4.3.
If the list price and the total discount amount are known, apply Formula 4.2b and rearrange for $N$ .

Assume a product with an MSRP of $100 receives a trade discount of 30% and a volume discount of 10%. Calculate the net price.

Step 1: The list price and discounts are

$L = \char36 100$
$d_1 = 0.30$
$d_2 = 0.10$ .

Step 2: List price is known, so skip this step.

Step 3: Apply Formula 4.3 to calculate the net price:

$N=\char36 100\times(1-0.30)\times(1-0.10)=\char36 63$

The net price is $63, which is illustrated in the following diagram:

A circle diagram illustrating pricing with two discounts. The circle represents the MSRP ($100.) The blue portion of the circle illustrates a 30% discount of $100 ($30.) The red portion of the circle illustrates a 10% discount of $70 ($7.) The green portion of the circle illustrates the net price ($63.)

If you are solely interested in converting multiple discounts into a single equivalent discount, you need only substitute into Formula 4.4. In the above example, the product received a trade discount of 30% and a volume discount of 10%. To calculate the single equivalent discount, apply Formula 4.4:

$\begin{array}{r} d_e_q_u_i_v=1-(1-0.30)\times(1-0.10)\\ d_e_q_u_i_v=1-(0.70)(0.90)\\ d_e_q_u_i_v=1-0.63=0.37 \end{array}$

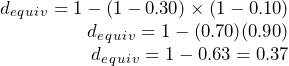
Therefore, whenever discounts of 30% and 10% are offered together, the single equivalent discount is 37%. Whether it is the multiple discounts or just the single equivalent discount that you apply to the list price, the net price calculated is always the same.

Order of Discounts:

The order of the discounts does not matter in determining the net price. Remember from the rules of BEDMAS that you can complete multiplication in any order. Therefore, in the above example you could have arrived at the $63 net price through the following calculation:

$\char36 100\times(1-0.10)\times(1-0.30)=\char36 63$

The order of the discounts does matter if trying to interpret the value of any single discount. If the trade discount is applied before the quantity discount and you are wanting to know the quantity discount amount, then the quantity discount needs to be second. Thus,

$\begin{array}{r} \char36 100\times(1-0.30)=\char36 70\\ \char36 70\times0.10=\char36 7 \end{array}$

which is the amount of the quantity discount.

Price Does Not Affect Single Equivalent Discount:

Notice in Formula 4.4 that the list price and the net price are not involved in the calculation of the single equivalent discount. When working with percentages, whether you have a net price of $6.30 and a list price of $10, or a net price of $63 and a list price of $100, the equivalent percentage always remains constant at 37%.

A common mistake when working with multiple discounts is to add the discounts together to calculate the single equivalent discount. This mistaken single discount is then substituted into Formula 4.1 to arrive at the wrong net price. Remember that if two discounts of 30% and 10% apply, you cannot sum these discounts. The second discount of 10% is applied on a smaller price tag, not the original price tag. To calculate the net price you must apply Formula 4.3.

If you happen to know any two of the net price ( $N$ ), list price ( $L$ ), or the total discount amount ( $D\char36$ ), then you could also use Formula 4.2 to solve for the single equivalent discount, $d_e_q_u_i_v$ .

For example, if you know the net price is $63 and the total discount amount for all discounts is $37, you could use Formula 4.2b to figure out that the list price is $100, then convert the discount amount into a percentage using Formula 4.2a. This method will also produce a single equivalent discount of 37%.

Another method of calculating the single equivalent discount is to recognize Formula 4.2a as an application of Formula 3.1 involving percent change. The variable d is a discount rate, which you interpret as a negative percent change. The discount amount, D, is the difference between the list price (representing the Old price) and the net price (representing the New price after the discount). Therefore, Formula 4.2a can be rewritten as follows:

$D\char36 =L\times d$

becomes

${\textrm{New }}-{\textrm{ Old }}={\textrm{ Old}}\times\Delta\%$

or

$\frac{{\textrm{New }}-{\textrm{ Old}}}{{\textrm{Old}}}=\Delta\%$

Therefore, any question about a single equivalent discount where net price and list price are known can be solved as a percent change. Using our ongoing net price example, you have:

$\begin{array}{r} \frac{\char36 63-\char36 100}{\char36 100}=-0.37 &{\textrm{or }\\ -37\% \end{array}$

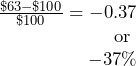
This is a discount of 37%.

Give It Some Thought:

3. If you are offered discounts in the amount of 25%, 15%, 10%, and 5%, will your total discount percent be 55%, less than 55%, or more than 55%?

Example 4.1D – Retailer Purchasing Ski-Doos with Multiple Discounts

A retail dealership purchases some Expedition TUV Yeti II Ski-Doos to stock in its stores. Examining the merchandising terms of the manufacturer, Bombardier, the dealership notices that it would be eligible to receive a 35% trade discount, 15% volume discount, and 3% loyalty discount. Because it is June and Ski-Doos are out of season, Bombardier offers a seasonal discount of 12% for purchases made before June 30. If the MSRP for the Ski-Doo is $12,399.00 and the dealership purchases this item on June 15, what price would it pay?

Plan:
You are looking for the net price that the retail dealership will pay for the Ski-Doo, or $N$ .

Understand:
Step 1: The retail dealership is eligible for all four discounts (it qualifies for the seasonal discount since it is purchasing before June 30). Therefore,

$L = \char36 12,399.00$
$d_1 = 0.35$
$d_2 = 0.15$
$d_3 = 0.03$
$d_4 = 0.12$

Step 2: You know the list price, so skip this step.

Step 3: Apply Formula 4.3.

Perform:
Step 3:

$\begin{array}{l} N=\char36 12,399\times(1-0.35)\times(1-0.15)\times(1-0.03)\times(1-0.12)\\ N=\char36 12,399\times0.65\times0.85\times0.97\times0.88=\char36 5,847.54 \end{array}$

Present:
After all four discounts, the retail dealership could purchase the Ski-Doo for $5,847.54.

Example 4.1E – Reducing Multiple Discounts to a Single Equivalent Discount

The retail dealership in Example 4.1D purchases more products subject to the same discounts. It needs to simplify its calculations. Using the information from Example 4.1D, what single equivalent discount is equal to the four specified discounts?

Plan:
You are looking for a single equivalent discount that is equal to the four discount percentages, or $d_e_q_u_i_v$ (or just $d$ ).

Understand:
You know the discount rates:

$d_1 = 0.35$
$d_2 = 0.15$
$d_3 = 0.03$
$d_4 = 0.12$

Apply Formula 4.4.

Perform:

$\begin{array}{r} d_e_q_u_i_v=1-(1-0.35)\times(1-0.15)\times(1-0.03)\times(1-0.12)\\ d_e_q_u_i_v=1-(0.65)(0.85)(0.97)(0.88)\\ d_e_q_u_i_v=1-0.471614=0.528386 &{\textrm{or}\\ 52.8386\% \end{array}$

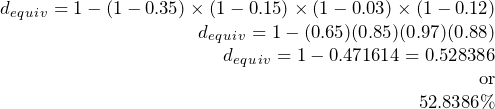
Present:
The retail dealership can apply a 52.8386% discount to all the products it purchases.

Example 4.1F – Making a Smart Consumer Purchase

You are shopping on Boxing Day for an 80″ HDTV. You have just one credit card in your wallet, a cashback Visa card, which allows for a 1% cash rebate on all purchases. While scanning flyers for the best deal, you notice that Visions is selling the TV for $5,599.99 including taxes, while Best Buy is selling it for $5,571.99 including taxes. However, because of a computer glitch Best Buy is unable to accept Visa today. Where should you buy your television?

Plan:
You want to know which store you should buy the television at. You must calculate the net price (N) for each of the stores.

Understand:
Step 1: You know the list price for each of the stores. You also know the discount available from Visa. Thus,

$L_B_e_s_t_B_u_y = \char36 5,571.99$ with no discounts since Visa cannot be used there
$L_V_i_s_i_o_n_s = \char36 5,599.99$ , $d = 0.01$ , since you can use your Visa card there

Step 2: List price is known, so skip this step.

Step 3: Apply Formula 4.1.

Perform:
Step 3:
Best Buy: No discounts apply, so the list price equals the net price.

$N=\char36 5,571.99$

Visions:

$N=\char36 5,599.99\times(1-0.01)=\char36 5,599.99\times0.99=\char36 5,543.99$

Present:
The net price for Visions is $5,543.99. You save $5,571.99 – $5,543.99 = $28.00 by purchasing your TV at Visions.

Example 4.1G – Understanding the Price

An advertisement claims that at 60% off, you are saving $18. However, today there is an additional 20% off. What price should you pay for this item? What percent savings does this represent?

Plan:
You are looking for how much you should pay after the discounts (N), and the single equivalent percentage that represents the two discounts (d_equiv or just d).

Understand:
Step 1: You know the discount amount for the first discount only, as well as the two discount rates:

$D\char36_1 = \char36 18$
$d_1 = 0.60$
$d_2 = 0.20$

Step 2: Calculate the list price by applying Formula 4.2a and rearranging for L.

Step 3: To calculate the net price, apply Formula 4.3.

Step 4: To calculate the single equivalent discount, apply Formula 4.4.

Perform:
Step 2:

$\begin{array}{r} \char36 18.00=L\times0.60\\ L=\char36 18.00\div0.6=\char36 30.00 \end{array}$

Step 3:

$N=\char36 30\times(1-0.60)\times(1-0.20)=\char36 30\times(0.40)\times(0.80)=\char36 9.60$

Step 4:

$\begin{array}{c} d_e_q_u_i_v=1-(1-0.60)\times(1-0.20)=1-(0.40)(0.80)=1-0.32=0.68 &{\textrm{or}\\ 68\% \end{array}$

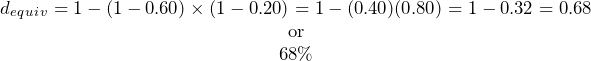
Present:
You should pay $9.60 for the item, which represents a 68% savings.

Give It Some Thought Answers

a. Exactly $10. The net price is the price after the discount.
b. Less than $10. The discount needs to be removed from the list price.
More than half. A 40% discount means that you will pay 60% of the list price.

Exercises

Round all money to two decimals and percentages to four decimals in each of the following questions.

Mechanics

For questions 1–4, solve for the unknown variables (identified with a ?) based on the information provided. “N/A” indicates that the particular variable is not applicable in the question.

	List Price or MRSP	First Discount	Second Discount	Third Discount	Net Price	Equivalent Single Discount Rate	Total Discount Amount
1.	$980.00	42%	N/A	N/A	?	N/A	?
2.	?	25%	N/A	N/A	$600.00	N/A	?
3.	$1,975.00	25%	15%	10%	?	?	?
4.	?	18%	4%	7%	$366.05	?	?

Applications

5. A wholesaler of stereos normally qualifies for a 35% trade discount on all electronic products purchased from its manufacturer. If the MSRP of a stereo is $399.95, what net price will the wholesaler pay?

6. Mary is shopping at the mall where she sees a sign that reads, “Everything in the store is 30% off, including sale items!” She wanders in and finds a blouse on the clearance rack. A sign on the clearance rack states, “All clearance items are 50% off.” If the blouse is normally priced at $69.49, what price should Mary pay for it?

7. A distributor sells some shoes directly to a retailer. The retailer pays $16.31 for a pair of shoes that has a list price of $23.98. What trade discount percent is the distributor offering to its retailers?

8. A retailer purchases supplies for its head office. If the retailer pays $16.99 for a box of paper and was eligible for a 15% volume discount, what was the original MSRP for the box of paper?

9. Mountain Equipment Co-op has purchased a college backpack for $29 after discounts of 30%, 8%, and 13%. What is the MSRP for the backpack? What single discount is equivalent to the three discounts?

10. Walmart purchased the latest CD recorded by Selena Gomez. It received a total discount of $10.08 off the MSRP for the CD, which represents a discount percent of 42%.
a. What was the MSRP?
b.What was the net price paid for the CD?

11. Best Buy just acquired an HP Pavilion computer for its electronics department. The net price on the computer is $260.40 and Best Buy receives discounts of 40% and 38%.
a. What single discount is equivalent to the two discounts?
b. What is the list price?
c. What is the total discount amount?

12. TELUS retails a Samsung cellphone at the MSRP of $399.99. TELUS can purchase the phone from its supplier and receive a 20% trade discount along with a 5% volume discount.
a. What is the single equivalent percent discount?
b. What net price does TELUS pay for the phone?
c. How much of a discount in dollars does this represent?

13. A wholesaler offers the following discounts: 10% seasonal discount for all purchases made between March 1 and May 1, 15% cumulative quantity discount whenever more than 5,000 units are purchased in any month, 5% loyalty discount for customers who have made regular purchases every month for at least one year, and a 33% trade discount to any retailer. Ed’s Retail Superstore makes a purchase of 200 watches, MSRP $10, from the wholesaler on April 29. This month alone, Ed’s has ordered more than 5,000 watches. However, Ed’s has purchased from the wholesaler for only the past six months. Determine the total price that Ed’s should pay for the watches.

14. If a distributor is eligible for a 60% trade discount, 5% volume discount, and 3% seasonal discount, what single equivalent discount rate would it be eligible to receive? If the trade discount is applied first and equals a trade discount of $48, calculate the net price for the item.

Challenge, Critical Thinking, & Other Applications

As mentioned previously, discount percentages share a commonality with negative percent changes (Section 2.1). Use the formulas from this chapter to solve questions 15–17 involving percent change.

15. A human resource manager needs to trim labour costs in the following year by 3%. If current year labour costs are $1,231,498, what are the labour costs next year?

16. At an accounting firm, the number of accountants employed is based on the ratio of 1:400 daily manual journal entries. Because of ongoing increases in automation, the number of manual journal entries declines at a constant rate of 4% per year. If current entries are 4,000 per year, how many years and days will it take until the firm needs to lay off one accountant? (Hint: An accountant is laid off when the number of journal entries drops below 3,600.)

17. An economist is attempting to understand how Canada reduced its national debt from 1999 to 2008. In 1999, Canada’s national debt was $554.143 billion. In 2008, the national debt stood at $457.637 billion. What percentage had the national debt been reduced by during this time period?

18. Sk8 is examining an invoice. The list price of a skateboard is $109.00, and the invoice states it received a trade discount of 15% and quantity discount of 10% as well as a loyalty discount. However, the amount of the loyalty discount is unspecified.
a. If Sk8 paid $80.88 for the skateboard, what is the loyalty discount percent?
b. If the loyalty discount is applied after all other discounts, what amount of loyalty dollars does Sk8 save per skateboard?

19. Currently, a student can qualify for up to six different tuition discounts at a local college based on such factors as financial need or corporate sponsorships. Mary Watson just applied to the college and qualifies for all six discounts: 20%, 15%, 23%, 5%, 3%, and 1%.
a. She is confused and wants the college to tell her what single discount percent she is receiving. What should the college tell her?
b. If her total list tuition comes to $6,435.00, how much should she pay?

20. Sumandeep is very loyal to her local hairstylist. Because she is loyal, her hairstylist gives her three different discounts: 10%, 5%, and 5%. These discounts amount to $14.08 in savings.
a. What was the list price her hairstylist charged her?
b. What amount did she pay her hairstylist?
c. If her hairstylist increases prices by 5%, what are the list price, net price, and total discount amount?

4.2 Markup

As you wait in line to purchase your Iced Caramel Macchiato at Starbucks, you look at the pricing menu and think that $4.99 seems like an awful lot of money for a frozen coffee beverage. Clearly, the coffee itself doesn’t cost anywhere near that much. But then gazing around the café, you notice the carefully applied colour scheme, the comfortable seating, the high-end machinery behind the counter, and a seemingly well-trained barista who answers customer questions knowledgeably. Where did the money to pay for all of this come from? You smile as you realize your $4.99 pays not just for the macchiato, but for everything else that comes with it.

The process of taking a product’s cost and increasing it by some amount to arrive at a selling price is called markup. This process is critical to business success because every business must ensure that it does not lose money when it makes a sale. From the consumer perspective, the concept of markup helps you make sense of the prices that businesses charge for their products or services. This in turn helps you to judge how reasonable some prices are (and hopefully to find better deals).

The Components in a Selling Price

Before you learn to calculate markup, you first have to understand the various components of a selling price. Then, in the next section, markup and its various methods of calculation will become much clearer.

When your business acquires merchandise for resale, this is a monetary outlay representing a cost. When you then resell the product, the price you charge must recover more than just the product cost. You must also recover all the selling and operating expenses associated with the product. Ultimately, you also need to make some money, or profit, as a result of the whole process.

Most people think that marking up a product must be a fairly complex process. It is not. Formula 4.5 illustrates the relationship between the three components of cost, expenses, and profits in calculating the selling price.

Formula 4.5 – The Selling Price of a Product

$S=C+E+P$

S is Selling Price: Once you calculate what the business paid for the product (cost), the bills it needs to cover (expenses), and how much money it needs to earn (profit), you arrive at a selling price by summing the three components.

C is Cost: The cost is the amount of money that the business must pay to purchase or manufacture the product. If manufactured, the cost represents all costs incurred to make the product. If purchased, this number results from applying an appropriate discount formula from Section 4.1. There is a list price from which the business will deduct discounts to arrive at the net price. The net price paid for the product equals the cost of the product. If a business purchases or manufactures a product for $10 then it must sell the product for at least $10. Otherwise, it fails to recover what was paid to acquire or make the product in the first place—a path to sheer disaster!

E is Expenses: Expenses are the financial outlays involved in selling the product. Beyond just purchasing the product, the business has many more bills to pay, including wages, taxes, leases, equipment, electronics, insurance, utilities, fixtures, décor, and many more. These expenses must be recovered and may be calculated as:

A fixed dollar amount per unit.
A percentage of the product cost. For example, if a business forecasts total merchandise costs of $100,000 for the coming year and total business expenses of $50,000, then it may set a general guideline of adding 50% ($50,000 ÷ $100,000) to the cost of a product to cover expenses.
A percentage of the product selling price based on a forecast of future sales. For example, if a business forecasts total sales of $250,000 and total business expenses of $50,000, then it may set a general guideline of adding 20% ($50,000 ÷ $250,000) of the selling price to the cost of a product to cover expenses.

P is Profit: Profit is the amount of money that remains after a business pays all of its costs and expenses. A business needs to add an amount above its costs and expenses to allow it to grow. If it adds too much profit, though, the product’s price will be too high, in which case the customer may refuse to purchase it. If it adds too little profit, the product’s price may be too low, in which case the customer may perceive the product as shoddy and once again refuse to purchase it. Many businesses set general guidelines on how much profit to add to various products. As with expenses, this profit may be expressed as:

A fixed dollar amount per unit.
A percentage of the product cost.
A percentage of the selling price.

How It Works

Follow these steps to solve pricing scenarios involving the three components:

Step 1: Four variables are involved in Formula 4.5. Identify the known variables. Note that you may have to calculate the product’s cost by applying the single or multiple discount formulas (Formulas 4.1 and 4.3, respectively). Pay careful attention to expenses and profits to capture how you calculate these amounts.

Step 2: Apply Formula 4.5 and solve for the unknown variable.

Assume a business pays a net price of $75 to acquire a product. Through analyzing its finances, the business estimates expenses at $25 per unit, and it figures it can add $50 in profit. Calculate the selling price.

Step 1: The net price paid for the product is the product cost. The known variables are:

$C = \char36 75$
$E = \char36 25$
$P = \char36 50$

Step 2: According to Formula 4.5, the unit selling price is:

$S=C+E+P=\char36 75+\char36 25+\char36 50=\char36 150$

In applying Formula 4.5 you must adhere to the basic rule of linear equations requiring all terms to be in the same unit. That is, you could use Formula 4.5 to solve for the selling price of an individual product, where the three components are the unit cost, unit expenses, and unit profit. When you add these, you calculate the unit selling price. Alternatively, you could use Formula 4.5 in an aggregate form where the three components are total cost, total expenses, and total profit. In this case, the selling price is a total selling price, which is more commonly known as total revenue. But you cannot mix individual components with aggregate components.

The most common mistake in working with pricing components occurs in the “Understand” portion of the PUPP model. It is critical to identify and label information correctly. You have to pay attention to details such as whether you are expressing the expenses in dollar format or as a percentage of either cost or selling price. Systematically work your way through the information provided piece by piece to ensure that you do not miss an important detail.

Give It Some Thought:

What three components make up a selling price? In what units are these components commonly expressed?
In what three ways are expenses and profits expressed?
What is the relationship between net price and cost?

Example 4.2A – Setting a Price on Fashion in Dollars

Mary’s Boutique purchases a dress for resale at a cost of $23.67. The owner determines that each dress must contribute $5.42 to the expenses of the store. The owner also wants this dress to earn $6.90 toward profit. What is the regular selling price for the dress?

Plan:
You are looking for the regular selling price for the dress, or $S$ .

Understand:
Step 1: The unit cost of the dress and the unit expense and the unit profit are all known:

$C = \char36 23.67$
$E = \char36 5.42$
$P = \char36 6.90$

Step 2: Apply Formula 4.5.

Perform:
Step 2:

$S=\char36 23.67+\char36 5.42+\char36 6.90=\char36 35.99$

Present:
Mary’s Boutique will set the regular price of the dress at $35.99.

Example 4.2B – Setting the Price Using Percentage of Cost

John’s Discount Store just completed a financial analysis. The company determined that expenses average 20% of the product cost and profit averages 15% of the product cost. John’s Discount Store purchases Chia Pets from its supplier for an MSRP of $19.99 less a trade discount of 45%. What will be the regular selling price for the Chia Pets?

Plan:
You are looking for the regular selling price for the Chia pets, or $S$ .

Understand:
Step 1: The list price, discount rate, expenses, and profit are known:

$L = \char36 19.99$
$d$ = 0.45
$E$ = 20% of cost, or 0.20C
$P$ = 15% of cost, or 0.15C

Although the cost of the Chia Pets is not directly known, you do know the MSRP (list price) and the trade discount. The cost is equal to the net price. Apply Formula 4.1.

Step 2: To calculate the selling price, apply Formula 4.5.

Perform:
Step 1:

$N=\char36 19.99\times(1-0.45)=\char36 19.99\times0.55=\char36 10.99=C$

Step 2:

$S=\char36 10.99+0.20C+0.15C$
$S=\char36 10.99+0.20(10.99)+0.15(\char36 10.99)$
$S=\char36 10.99+\char36 2.20+\char36 1.65=\char36 14.84$

Present:
John’s Discount Store will sell the Chia Pet for $14.84.

A circle diagram illustrating the price components for a Chia Pet. The circle represents the selling price of $14.84. The blue portion of the circle represents the cost ($10.99.) The red portion of the circle represents expenses ($2.20.) The green portion of the circle represents profit ($1.65.)

Example 4.2C – Setting the Price Using Percentage of Selling Price

Based on last year’s results, Benthal Appliance learned that its expenses average 30% of the regular selling price. It wants a 25% profit based on the selling price. If Benthal Appliance purchases a fridge for $1,200, what is the regular unit selling price?

Plan:
You are looking for the regular unit selling price for the fridge, or $S$ .

Understand:
Step 1: The cost, expenses, and profit for the fridge are known:

$E$ = 30% of $S$ , or $0.3S$
$P$ = 25% of $S$ , or $0.25S$
$C$ = $1,200.00

Step 2: Apply Formula 4.5.

Perform:
Step 2:

$S=\char36 1,200.00+0.3S+0.25S$
$S=\char36 1,200+0.55S$
$S-0.55S=\char36 1,200.00$
$0.45S=\char36 1,200.00$
$S=\char36 2,666.67$

Present
Benthal Appliance should set the regular selling price of the fridge at $2,666.67.

A circle diagram illustrating price components for a fridge. The circle represents the regular selling price ($2,666.67.) The blue portion of the circle represents cost ($1,200.00). The red portion of the circle represents expenses [0.3($2,666.67) = $800.00.] The green portion of the circle represents profit [0.25($2,666.67) = $666.67]

Example 4.2D – Using Selling Price to Figure Out the Cost

If a company knows that its profits are 15% of the selling price and expenses are 30% of cost, what is the cost of an MP3 player that has a regular selling price of $39.99?

Plan:
You are looking for the cost of the MP3 player, or $C$ .

Understand:
Step 1: The expenses, profits, and the regular unit selling price are as follows:

$S$ = $39.99
$P$ = 15% of $S$ , or $0.15S$
$E$ = 30% of cost, or $0.3C$

Step 2: Apply Formula 4.5, rearranging for $C$ .

Perform:
Step 2:

$\char36 39.99=C+0.3C+0.15(\char36 39.99)$
$\char36 39.99=1.3C+\char36 6.00$
$\char36 33.99=1.3C$
$\char36 26.15=C$

Present:
The cost of the MP3 Player is $26.15.

A circle diagram illustrating price components of an MP3 player. The circle represents the regular selling price ($39.99.) The blue portion of the circle represents cost ($26.15.) The red portion of the circle represents expenses [0.3($26.15) = $7.84.] The green portion of the circle represents profit [0.13($39.99) = $6.00.]

Example 4.2E – Determining Profitability

Peak of the Market considers setting the regular unit selling price of its strawberries at $3.99 per kilogram. If it purchases these strawberries from the farmer for $2.99 per kilogram and expenses average 40% of product cost, does Peak of the Market make any money?

Plan:
In asking whether Peak of the Market makes money, you are looking for the profit, or $P$ .

Understand:
Step 1: The cost, expenses, and proposed regular unit selling price for the strawberries are as follows:

$S$ = $3.99
$C$ = $2.99
$E$ = 40% of cost, or $0.4C$

Step 2: Apply Formula 4.5, rearranging for $P$ .

Perform:
Step 2:

$\char36 3.99=\char36 2.99+0.4(\char36 2.99)+P$
$\char36 3.99=\char36 4.19+P$
$-\char36 0.20=P$

Present:
The negative sign on the profit means that Peak of the Market would take a loss of $0.20 per kilogram if it sells the strawberries at $3.99. Unless Peak of the Market has a marketing reason or sound business strategy for doing this, the company should reconsider its pricing.

Calculating the Markup Dollars

Most companies sell more than one product, each of which has different price components with varying costs, expenses, and profits. Can you imagine trying to compare 50 different products, each with three different components? You would have to juggle 150 numbers! To make merchandising decisions more manageable and comparable, many companies combine expenses and profit together into a single quantity, either as a dollar amount or a percentage. This section focuses on the markup as a dollar amount.

One of the most basic ways a business simplifies its merchandising is by combining the dollar amounts of its expenses and profits together as expressed in Formula 4.6.

Formula 4.6 – Markup Amount

$M\char36 =E+P$

$M\char36$ is Markup Amount: Markup is taking the cost of a product and converting it into a selling price. The markup amount represents the dollar amount difference between the cost and the selling price.

$E$ is Expenses: The expenses associated with the product.

$P$ is Profit: The profit earned when the product sells.

Note that since the markup amount ( $M\char36$ ) represents the expenses ( $E$ ) and profit ( $P$ ) combined, you can substitute the variable for markup amount into Formula 4.5 to create Formula 4.7, which calculates the regular selling price.

Formula 4.7 – Selling Price Using Markup

$S=C+M\char36$

$S$ is Selling Price: The regular selling price of the product.

$C$ is Cost: The amount of money needed to acquire or manufacture the product. If the product is being acquired, the cost is the same amount as the net price paid.

$M\char36$ is Markup Amount: From Formula 4.6, this is the single number that represents the total of the expenses and profit.

How It Works

Follow these steps when you work with calculations involving the markup amount:

Step 1: You require three variables in either Formula 4.6 or Formula 4.7. At least two of the variables must be known. If the amounts are not directly provided, you may need to calculate these amounts by applying other discount or markup formulas.

Step 2: Solve either Formula 4.6 or Formula 4.7 for the unknown variable.

Recall from Example 4.2D that the MP3 player’s expenses are $7.84, the profit is $6.00, and the cost is $26.15. Calculate the markup amount and the selling price.

Step 1: The known variables are

$E$ = $7.84
$P$ = $6.00
$C$ = $26.15.

Step 2: According to Formula 4.6, the markup amount is the sum of the expenses and profit, or

$M\char36 =\char36 7.84+\char36 6.00=\char36 13.84$ .

Applying Formula 4.7, add the markup amount to the cost to arrive at the regular selling price, resulting in

$S=\char36 26.15+\char36 13.84=\char36 39.99$

You might have already noticed that many of the formulas in this chapter are interrelated. The same variables appear numerous times but in different ways. To help visualize the relationship between the various formulas and variables, many students have found it helpful to create a markup chart, as shown below.

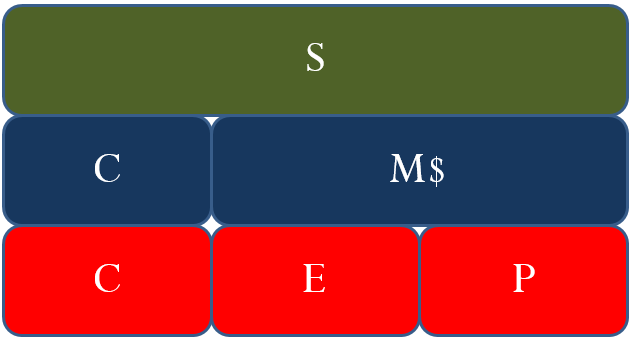
A chart demonstrating the relationships between Formulas 4.5, 4.6, and 4.7. (Described below.)

This chart demonstrates the relationships between Formulas 4.5, 4.6, and 4.7. It is evident that the selling price (the green line) consists of cost, expenses, and profit (the red line representing Formula 4.5); or it can consist of cost and the markup amount (the blue line representing Formula 4.7). The markup amount on the blue line consists of the expenses and profit on the red line (Formula 4.6).

Example 4.2F – Markup as a Dollar Amount

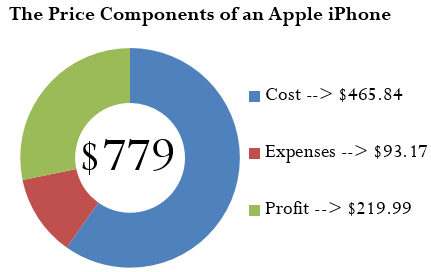
A cellular retail store purchases an iPhone with an MSRP of $779 less a trade discount of 35% and volume discount of 8%. The store sells the phone at the MSRP.
a. What is the markup amount?
b. If the store knows that its expenses are 20% of the cost, what is the store’s profit?

Plan:
First of all, you need to calculate the markup amount ( $M\char36$ ). You also want to find the store’s profit ( $P$ ).

Understand:
Step 1: The smartphone MSRP and the two discounts are known, along with the expenses and selling price:

$L$ = $270
$d_1$ = 0.35
$d_2$ = 0.08
$E$ = 20% of cost, or $0.2C$
$S$ = $779

Calculate the cost of the iPhone by applying Formula 4.3.

Step 2: Calculate the markup amount using Formula 4.7.

Calculate the profit by applying Formula 4.6, rearranging for $P$ .

Perform:
Step 1:

$N=\char36 779.00\times(1-0.35)\times(1-0.08)$
$N=\char36 779.00\times0.65\times0.92=\char36 465.84=C$

Step 2:

$\char36 779.00=\char36 465.84+M\char36$
$\char36 313.16=M\char36$

$\char36 313.16=0.2(\char36 465.84)+P$
$\char36 313.16=\char36 93.17+P$
$\char36 219.99=P$

Present:
The markup amount for the iPhone is $313.16. When the store sells the phone for $779.00, its profit is $219.99.

A circle diagram illustrating the price components of an Apple iPhone. The circle represents the selling price ($779.00). The blue portion of the circle represents the cost ($465.84). The red portion of the circle represents expenses ($93.17). The green portion of the circle represents profit ($219.99.)

Calculating the Markup Percent

It is important to understand markup in terms of the actual dollar amount; however, it is more common in business practice to calculate the markup as a percentage. There are three benefits to converting the markup dollar amount into a percentage:

Easy comparison of different products having vastly different price levels and costs, to help you see how each product contributes toward the financial success of the company. For example, if a chocolate bar has a 50¢ markup included in a selling price of $1, while a car has a $1,000 markup included in a selling price of $20,000, it is difficult to compare the profitability of these items. If these numbers were expressed as a percentage of the selling price such that the chocolate bar has a 50% markup and the car has a 5% markup, it is clear that more of every dollar sold for chocolate bars goes toward list profitability.
Simplified translation of costs into a regular selling price—a task that must be done for each product, making it helpful to have an easy formula, especially when a company carries hundreds, thousands, or even tens of thousands of products. For example, if all products are to be marked up by 50% of cost, an item with a $100 cost can be quickly converted into a selling price of $150.
An increased understanding of the relationship between costs, selling prices, and the list profitability for any given product. For example, if an item selling for $25 includes a markup on selling price of 40% (which is $10), then you can determine that the cost is 60% of the selling price ($15) and that $10 of every $25 item sold goes toward list profits.

You can translate the markup dollars into a percentage using two methods, which express the amount either as a percentage of cost or as a percentage of selling price:

Method 1: Markup as a Percentage of Cost.
This method expresses the markup rate using cost as the base. Many companies use this technique internally because most accounting is based on cost information. The result, known as the markup on cost percentage, allows a reseller to convert easily from a product’s cost to its regular unit selling price.
Method 2: Markup as a Percentage of Selling Price.
This method expresses the markup rate using the regular selling price as the base. Many other companies use this method, known as the markup on selling price percentage, since it allows for quick understanding of the portion of the selling price that remains after the cost of the product has been recovered. This percentage represents the list profits before the deduction of expenses and therefore is also referred to as the list profit margin.

The markup on cost percentage is expressed in Formula 4.8, while the markup on selling price percentage is expressed in Formula 4.9.

Formula 4.8 – Markup On Cost Percentage

$MoC\%=\frac{M\char36}{C}\times100$

$MoC\%$ is Markup on Cost Percentage: This is the percentage by which the cost of the product needs to be increased to arrive at the selling price for the product.

$M\char36$ is Markup Amount: The total dollars of the expenses and the profits; this total is the difference between the cost and the selling price.

$C$ is Cost: The amount of money needed to acquire or manufacture the product. If the product is being acquired, the cost is the same amount as the net price paid.

× 100 is Percent Conversion: The markup on cost is always a percentage.

Formula 4.9 – Markup On Selling Price Percentage

$MoS\%=\frac{M\char36}{S}\times100$

$MoS\%$ is Markup on Selling Price Percentage: This is the percentage of the selling price that remains available as list profits after the cost of the product is recovered.

$M$ is Markup Amount: The total dollars of the expenses and the profits; this total is the difference between the cost and the selling price.

$S$ is Selling Price: The regular selling price of the product.

× 100 is Percent Conversion: The markup on cost is always a percentage.

How It Works

Refer back to the steps in calculating markup. The steps you must follow for calculations involving markup percent are almost identical to those for working with markup dollars:

Step 1: Three variables are required in either Formula 4.8 or Formula 4.9. For either formula, at least two of the variables must be known. If the amounts are not directly provided, you may need to calculate these amounts by applying other discount or markup formulas.

Step 2: Solve either Formula 4.8 or Formula 4.9 for the unknown variable.

Continuing to work with Example 4.2D, recall that the cost of the MP3 player is $26.15, the markup amount is $13.84, and the selling price is $39.99. Calculate both markup percentages.

Step 1: The known variables are

$C$ = $26.15
$M\char36$ = $13.84
$S$ = $39.99.

Step 2: To calculate the markup on cost percentage, apply Formula 4.8:

$MoC\%=\frac{\char36 13.84}{\char36 26.15}\times100=52.9254\%$

In other words, you must add 52.9254% of the cost on top of the unit cost to arrive at the regular unit selling price of $39.99.

To calculate the markup on selling price percentage, apply Formula 4.9:

$MoS\%=\frac{\char36 13.84}{\char36 39.99}\times100=34.6087\%$

In other words, 34.6087% of the selling price represents list profits after the business recovers the $26.15 cost of the MP3 player.

Businesses are very focused on profitability. Your Texas Instruments BAII Plus calculator is programmed with the markup on selling price percentage. The function is located on the second shelf above the number three. To use this function, open the window by pressing 2nd 3. You can scroll between lines using your ↑ and ↓ arrows. There are three variables:

CST is the cost. Use the symbol $C$ .
SEL is the selling price. Use the symbol $S$ .
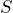MAR is the markup on selling price percentage. Use the symbol $MoS\%$ .

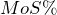As long as you know any two of the variables, you can solve for the third. Enter any two of the three variables (you need to press ENTER after each), making sure the window shows the output you are seeking, and press CPT.

Merchandising involves many variables. Nine formulas have been established so far, and a few more are yet to be introduced. Though you may feel bogged down by all of these formulas, just remember that you have encountered most of these merchandising concepts since you were very young and that you interact with retailers and pricing every day. This chapter merely formalizes calculations you already perform on a daily basis, whether at work or at home. The calculation of discounts is no different than going to Walmart and finding your favourite CD on sale. You know that when a business sells a product, it has to recoup the cost of the product, pay its bills, and make some money. And you have worked with percentages since elementary school.

Do not get stuck in the formulas. Think about the concept presented in the question. Change the scenario of the question and put it in the context of something more familiar. Ultimately, if you really have difficulties then look at the variables provided and cross-reference them to the merchandising formulas. Your goal is to find formulas in which only one variable is unknown. These formulas are solvable. Then ask yourself, “How does knowing that new variable help solve any other formula?”

You do not need to get frustrated. Just be systematic and relate the question to what you already know.

The triangle method simplifies rearranging both Formulas 4.8 and 4.9 to solve for other unknown variables as illustrated in the figure below.

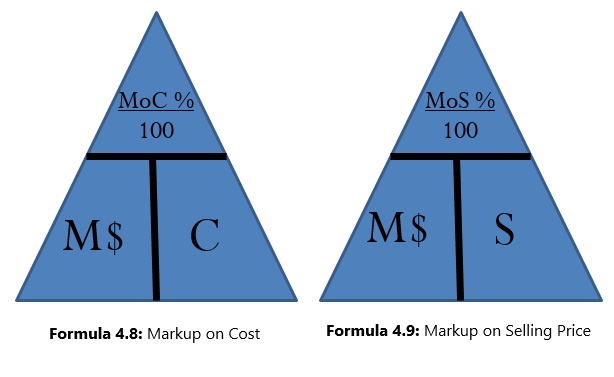
Sometimes you need to convert the markup on cost percentage to a markup on selling price percentage, or vice versa. Two shortcuts allow you to convert easily from one to the other:

$MoC\%=\frac{MoS\%}{1-MoS\%}$

$MoS\%=\frac{MoC\%}{1+MoC\%}$

Notice that these formulas are very similar. How do you remember whether to add or subtract in the denominator? In normal business situations, the $MoC\%$ is always larger than the $MoS\%$ . Therefore, if you are converting one to the other you need to identify whether you want the percentage to become larger or smaller.

To calculate 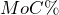$MoC\%$ , you want a larger percentage. Therefore, make the denominator smaller by subtracting 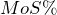$MoS\%$ from 1.
To calculate 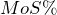$MoS\%$ , you want a smaller percentage. Therefore, make the denominator larger by adding 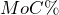$MoC\%$ to 1.

Give It Some Thought:

Answer the following true/false questions.

4. The markup on selling price percentage can be higher than 100%.

5. The markup dollar amount can be more than the selling price.

6. The markup on cost percentage can be higher than 100%.

7. The markup on cost percentage in most business situations is higher than the markup on selling price percentage.

8. If you know the markup on cost percentage and the cost, you can calculate a selling price.

9. If you know the markup on selling price percentage and the cost, you can calculate a selling price.

Example 4.2G – Markup as a Percentage

A large national retailer wants to price a Texas Instruments BAII Plus calculator at the MSRP of $39.99. The retailer can acquire the calculator for $17.23.
a. What is the markup on cost percentage?
b. What is the markup on selling price percentage?

Plan:
You have been asked to solve for the markup on cost percentage ( $MoC\%$ ) and the markup on selling price percentage ( $MoS\%$ ).

Understand:
Step 1: The regular unit selling price and the cost are provided:

$S$ = $39.99
$C$ = $17.23

You need the markup dollars. Apply Formula 4.7, rearranging for $M\char36$ .

Step 2: To calculate markup on cost percentage, apply Formula 4.8.

To calculate markup on selling price percentage, apply Formula 4.9.

Perform:
Calculator Instructions:

CST

SEL

MAR

17.23

39.99

Answer:
56.9142

Step 1:

$\char36 39.99=\char36 17.23+M\char36$
$\char36 22.76=M\char36$

Step 2:

$MoC\%=\frac{\char36 22.76}{\char36 17.23}\times100=132.0952\%$

$MoS\%=\frac{\char36 22.76}{\char36 39.99}\times100=56.9142\%$

Present:
The markup on cost percentage is 132.0952%. The markup on selling price percentage is 56.9142%.

Break-Even Pricing

In running a business, you must never forget the “bottom line.” In other words, if you fully understand how your products are priced, you will know when you are making or losing money. Remember, if you keep losing money you will not stay in business for long! 15% of new businesses will not make it past their first year, and 49% fail in their first five years. This number becomes even more staggering with an 80% failure rate within the first decade.^[1] Do not be one of these statistics! With your understanding of markup, you now know what it takes to break even in your business. Break-even means that you are earning no profit, but you are not losing money either. Your profit is zero.

If the regular unit selling price must cover three elements—cost, expenses, and profit—then the regular unit selling price must exactly cover your costs and expenses when the profit is zero. In other words, if Formula 4.5 is modified to calculate the selling price at the break-even point ( $S_B_E$ ) with $P$ =0, then:

$S_B_E=C+E$

This is not a new formula. It just summarizes that at break-even there is no profit or loss, so the profit ( $P$ ) is eliminated from the formula.

How It Works

The steps you need to calculate the break-even point are no different from those you used to calculate the regular selling price. The only difference is that the profit is always set to zero.

Recall Example 4.2D that the cost of the MP3 player is $26.15 and expenses are $7.84.

The break-even price ( $S_B_E$ ) is

$\char36 26.15+\char36 7.84=\char36 33.99$

This means that if the MP3 player is sold for anything more than $33.99, it is profitable; if it is sold for less, then the business does not cover its costs and expenses and takes a loss on the sale.

Example 4.2H – Knowing Your Break-Even Price

John is trying to run an eBay business. His strategy has been to shop at local garage sales and find items of interest at a great price. He then resells these items on eBay. On John’s last garage sale shopping spree, he only found one item—a Nintendo Wii that was sold to him for $100. John’s vehicle expenses (for gas, oil, wear/tear, and time) amounted to $40. eBay charges a $2.00 insertion fee, a flat fee of $2.19, and a commission of 3.5% based on the selling price less $25. What is John’s minimum list price for his Nintendo Wii to ensure that he at least covers his expenses?

Plan:
You are trying to find John’s break-even selling price ( $S_B_E$ ).

Understand:
Step 1: John’s cost for the Nintendo Wii and all of his associated expenses are as follows:

$C$ = $100.00
$E$ (vehicle) = $40.00
$E$ (insertion) = $2.00
$E$ (flat) = $2.19
$E$ (commission) = 3.5%(S_BE − $25.00)

You have four expenses to add together that make up the $E$ in the formula.

Step 2: Formula 4.5 states $S=C+E+P$ . Since you are looking for the break-even point, then $P$ is set to zero and $S_B_E=C+E$ .

Perform:
Step 1:

$E=\char36 40.00+\char36 2.00+\char36 2.19+3.5\%(S_B_E-\char36 25.00)$
$E=\char36 44.19+0.035(S_B_E-\char36 25.00)=\char36 44.19+0.035S_B_E-\char36 0.875$
$E=\char36 43.315+0.035S_B_E$

Step 2:

$S_B_E=\char36 100+\char36 43.315+0.035S_B_E$
$S_B_E=\char36 143.315+0.035S_B_E$
$S_B_E-0.035S_B_E=\char36 143.315$
$0.965S_B_E=\char36 143.315$
$S_B_E=\char36 148.51$

Present:
At a price of $148.51 John would cover all of his costs and expenses but realize no profit or loss. Therefore, $148.51 is his minimum price.

Give It Some Thought Answers

Cost, expenses, and profit. They are expressed either per unit or as a total.
A specific dollar amount, a percentage of cost, or a percentage of the selling price.
The net price paid for a product is the same as the cost of the product.
False. The markup amount is a portion of the selling price and therefore is less than 100%.
False. The markup amount plus the cost equals the selling price. It must be less than the selling price.
True. A cost can be doubled or tripled (or increased even more) to reach the price.
True. The base for markup on cost percentage is smaller, which produces a larger percentage.
True. You could combine Formulas 4.7 and 4.8 to arrive at the selling price.
True. You could convert the 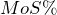$MoS\%$ to a $MoC\%$ and solve as in the previous question.

Exercises

Round all money to two decimals and percentages to four decimals for each of the following exercises.

Mechanics

For questions 1–8, solve for the unknown variables (identified with a ?) based on the information provided.

Regular Unit Selling Price

Cost

Expenses

Profit

Markup Amount

Break-Even Price

Markup on Cost

Markup on Selling Price

1.

?

$188.42

$48.53

$85.00

?

2.

$999.99

?

30% of $C$

23% of $C$

?

3.

?

10% of $S$

$183.28

?

155%

?

4.

$274.99

?

20% of $S$

?

35%

5.

?

45% of $C$

?

$540.00

$1,080.00

?

6.

?

$200 less 40%

?

15% of $S$

?

68%

?

7.

?

$100.00

?

$275.00

?

19%

8.

?

15% of $C$

12% of $S$

?

$253.00

?

Applications

9. If a pair of sunglasses sells at a regular unit selling price of $249.99 and the markup is always 55% of the regular unit selling price, what is the cost of the sunglasses?

10. A transit company wants to establish an easy way to calculate its transit fares. It has determined that the cost of a transit ride is $1.00, with expenses of 50% of cost. It requires $0.75 profit per ride. What is its markup on cost percentage?

11. Daisy is trying to figure out how much negotiating room she has in purchasing a new car. The car has an MSRP of $34,995.99. She has learned from an industry insider that most car dealerships have a 20% markup on selling price. What does she estimate the dealership paid for the car?

12. The markup amount on an eMachines desktop computer is $131.64. If the machine regularly retails for $497.25 and expenses average 15% of the selling price, what profit will be earned?

13. Manitoba Telecom Services (MTS) purchases an iPhone for $749.99 less discounts of 25% and 15%. MTS’s expenses are known to average 30% of the regular unit selling price.
a. What is the regular unit selling price if a profit of $35 per iPhone is required?
b. What are the expenses?
c. What is the markup on cost percentage?
d. What is the break-even selling price?

14. A snowboard has a cost of $79.10, expenses of $22.85, and profit of $18.00.
a. What is the regular unit selling price?
b. What is the markup amount?
c. What is the markup on cost percentage?
d. What is the markup on selling price percentage?
e. What is the break-even selling price? What is the markup on cost percentage at this break-even price?

Challenge, Critical Thinking, & Other Applications

15. A waterpark wants to understand its pricing better. If the regular price of admission is $49.95, expenses are 20% of cost, and the profit is 30% of the regular unit selling price, what is the markup amount?

16. Sally works for a skateboard shop. The company just purchased a skateboard for $89.00 less discounts of 22%, 15%, and 5%. The company has standard expenses of 37% of cost and desires a profit of 25% of the regular unit selling price. What regular unit selling price should Sally set for the skateboard?

17. If an item has a 75% markup on cost, what is its markup on selling price percentage?

18. A product received discounts of 33%, 25%, and 5%. A markup on cost of 50% was then applied to arrive at the regular unit selling price of $349.50. What was the original list price for the product?

19. Mountain Equipment Co-op (MEC) wants to price a new backpack. The backpack can be purchased for a list price of $59.95 less a trade discount of 25% and a quantity discount of 10%. MEC estimates expenses to be 18% of cost and it must maintain a markup on selling price of 35%.
a. What is the cost of backpack?
b. What is the markup amount?
c. What is the regular unit selling price for the backpack?
d. What profit will Mountain Equipment Co-op realize?
e. What happens to the profits if it sells the backpack at the MSRP instead?

20. Costco can purchase a bag of Starbucks coffee for $20.00 less discounts of 20%, 15%, and 7%. It then adds a 40% markup on cost. Expenses are known to be 25% of the regular unit selling price.
a. What is the cost of the coffee?
b. What is the regular unit selling price?
c. How much profit will Costco make on a bag of Starbucks coffee?
d. What markup on selling price percentage does this represent?
e. Repeat questions (a) through (d) if the list price changes to $24.00.

4.3 Markdown

Flashy signs in a retail store announce, “40% off, today only!” Excitedly you purchase three tax-free products with regular price tags reading $100, $250, and $150. The cashier processing the transaction informs you that your total is $325. You are about to hand over your credit card when something about the total makes you pause. The regular total of all your items is $500. If they are 40% off, you should receive a $200 deduction and pay only $300. The cashier apologizes for the mistake and corrects your total.

Although most retail stores use automated checkout systems, these systems are ultimately programmed by human beings. A computer system is only as accurate as the person keying in the data. A study by the Competition Bureau revealed that 6.3% of items at various retail stores scanned incorrectly. The average error spread is up to 13% around the actual product’s price!^[2] Clearly, it is important for you as a consumer to be able to calculate markdowns.

Businesses must also thoroughly understand markdowns so that customers are charged accurately for their purchases. Businesses must always comply with the Competition Act of Canada, which specifically defines legal pricing practices. If your business violates this law, it faces severe penalties.

The Importance of Markdowns

A markdown is a reduction from the regular selling price of a product resulting in a lower price. This lower price is called the sale price to distinguish it from the selling price.

Many people perceive markdowns as a sign of bad business management decisions. However, in most situations this is not true. Companies must always attempt to forecast the future. In order to stock products, a reseller must estimate the number of units that might sell in the near future for every product that it carries. This is both an art and a science. While businesses use statistical techniques that predict future sales with a relative degree of accuracy, consumers are fickle and regularly change shopping habits. Markdowns most commonly occur under four circumstances:

Clearing Out Excess or Unwanted Inventory. In these situations, the business thought it could sell 100 units; however, consumers purchased only 20 units. In the case of seasonal inventory, such as Christmas items on Boxing Day, the retailer wishes to avoid packing up and storing the inventory until the next season.
Clearing Out Damaged or Discontinued Items. Selling a damaged product at a discount is better than not selling it at all. When products are discontinued, this leaves shelf space underused, so it is better to clear the item out altogether to make room for profitable items that can keep the shelves fully stocked.
Increasing Sales Volumes. Sales attract customers because almost everyone loves a deal. Though special marketing events such as a 48 hour sale reduce the profitability per unit, by increasing the volume sold these sales can lead to a greater profit overall.
Promoting Add-On Purchases. Having items on sale attracts customers to the store. Many times customers will not only purchase the item on sale but also, as long as they are on the premises, grab a few other items, which are regularly priced and very profitable. Like many others, you may have walked into Target to buy one item but left with five instead.

Markdowns are no different from offering a discount. Recall from Section 4.1 that one of the types of discounts is known as a sale discount. The only difference here lies in choice of language. Markdowns are common, so you will find it handy to adapt the discount formulas to the application of markdowns, replacing the symbols with ones that are meaningful in merchandising. Formula 4.1, introduced in Section 4.1, calculates the net price for a product after it receives a single discount:

$N=L\times(1-d)$

Formula 4.10 adapts this formula for use in markdown situations.

Formula 4.10 – The Sale Price Of A Product

$S_o_n_s_a_l_e=S\times(1-d)$

$S_o_n_s_a_l_e$ is Sale Price: The sale price is the price of the product after reduction by the markdown percent. Conceptually, the sale price is the same as the net price.

$S$ is Selling Price: The regular selling price of the product before any discounts. The higher price is the list price. In merchandising questions, this dollar amount may or may not be a known variable. If the selling price is unknown, you must calculate it using an appropriate formula or combination of formulas from either Section 4.1 or Section 4.2.

$d$ is Markdown Rate: A markdown rate is the same as a sale discount rate. Therefore you use the same discount rate symbol from Section 4.1 to represent the percentage (in decimal format) by which you reduce the selling price. As in Formula 4.1, note that you are interested in calculating the sale price and not the amount saved. Thus, you take the markdown rate away from 1 to find out the rate owing.

In markdown situations, the selling price and the sale price are different variables. The sale price is always less than the selling price. In the event that a regular selling price has more than one markdown percent applied to it, you can extend Formula 4.10 in the same manner that Formula 4.3 calculated multiple discounts.

If you are interested in the markdown amount in dollars, recall that Formula 4.2 calculates the discount amount in dollars. Depending on what information is known, the formula has two variations:

Formula 4.2a: $D\char36=L\times d$
Formula 4.2b: $D\char36=L-N$

Formulas 4.11a and 4.11b adapt these formulas to markdown situations.

Formula 4.11a and 4.11b – Markdown Amount

Formula 4.11a

$D\char36=S\times d$

Formula 4.11b

$D\char36=S-S_o_n_s_a_l_e$

$D\char36$ is Markdown Amount: You determine the markdown amount using either formula depending on what information is known. If you know the selling price and markdown percent, apply Formula 4.11a. If you know the selling price and sale price, apply Formula 4.11b.

$S$ is Selling Price: The regular selling price before you apply any markdown percentages.

$d$ is Markdown Rate: the percentage of the selling price to be deducted (in decimal format). In this case, because you are interested in figuring out how much the percentage is worth, you do not take it away from 1 as in Formula 4.10.

$S_o_n_s_a_l_e$ is Sale Price: The price after you have deducted all markdown percentages from the regular selling price.

The final markdown formula reflects the tendency of businesses to express markdowns as percentages, facilitating easy comprehension and comparison. Recall Formula 4.9 from Section 4.2, which calculated a markup on selling price percent:

$MoS\%=\frac{M\char36}{S}\times100$

Formula 4.12 adapts this formula to markdown situations.

Formula 4.12 – Markdown Percentage

$d=\frac{D\char36}{S}\times100$

$d$ is Markdown Percentage: You always deduct a markdown amount from the regular selling price of the product. Therefore, you always express the markdown percent as a percentage of the selling price. Use the same symbol for a discount rate, since markdown rates are synonymous with sale discounts.

$D\char36$ is Markdown Amount: The total dollar amount deducted from the regular selling price.

$S$ is Selling Price: The regular selling price of the product before any discounts.

100 is Percent Conversion: The markdown is always expressed as a percentage.

How It Works

Follow these steps to calculate a markdown:

Step 1: Across all three markdown formulas, the four variables consist of the selling price ( $S$ ), sale price ( $S_o_n_s_a_l_e$ ), markdown dollars ( $D\char36$ ), and markdown rate ( $d$ ). Identify which variables are known. Depending on the known information, you may have to calculate the selling price using a combination of discount and markup formulas.

Step 2: Apply one or more of Formulas 4.10, 4.11a, 4.11b, and 4.12 to calculate the unknown variable(s). In the event that multiple markdown rates apply, extend Formula 4.10 to accommodate as many markdown rates as required.

Recall from Section 4.2 the example of the MP3 player with a regular selling price of $39.99. Assume the retailer has excess inventory and places the MP3 player on sale for 10% off. What is the sale price and markdown amount?

Step 1: The selling price and markdown percent are $S$ = $39.99 and $d$ = 0.10, respectively.

Step 2: Apply Formula 4.10 to calculate the sale price, resulting in

$S_o_n_s_a_l_e=\char36 39.99\times(1-0.10)=\char36 35.99$ .

You could use either of Formulas 4.11a or 4.11b to calculate the markdown amount since the selling price, sale price, and markdown percent are all known. Arbitrarily choosing Formula 4.11a, you calculate a markdown amount of

$D\char36=\char36 39.99\times0.10=\char36 4.00$

Therefore, if the retailer has a 10% off sale on the MP3 players, it marks down the product by $4.00 and retails it at a sale price of $35.99.

Just as in Section 4.2, avoid getting bogged down in formulas. Recall that the three formulas for markdowns are not new formulas, just adaptations of three previously introduced concepts. As a consumer, you are very experienced with endless examples of sales, bargains, discounts, blowouts, clearances, and the like. Every day you read ads in the newspaper and watch television commercials advertising percent savings. This section simply crystallizes your existing knowledge. If you are puzzled by questions involving markdowns, make use of your shopping experiences at the mall!

Three of the formulas introduced in this section can be solved for any variable through algebraic manipulation when any two variables are known. Recall that the triangle technique helps you remember how to rearrange these formulas, as illustrated here.

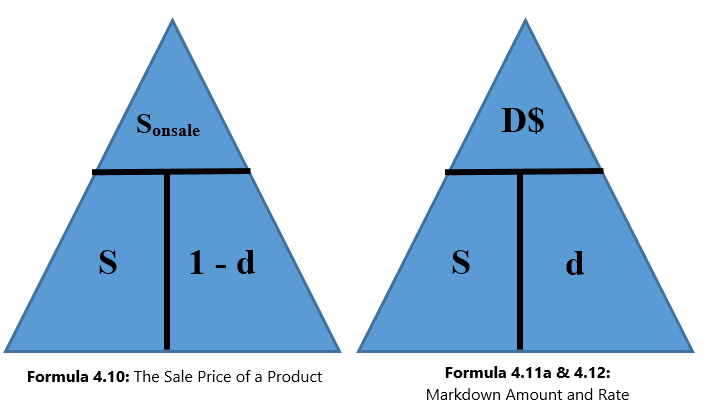
Example 4.3A – Determining the Sale Price and Markdown Amount

The MSRP for the “Guitar Hero: World Tour” video game is $189.99. Most retail stores sell this product at a price in line with the MSRP. You have just learned that a local electronics retailer is selling the game for 45% off. What is the sale price for the video game and what dollar amount is saved?

Plan:
There are two unknown variables. The first is the video game’s sale price ( $S_o_n_s_a_l_e$ ). The second is the markdown amount ( $D\char36$ ) that is realized at that sale price.

Understand:
Step 1: The regular selling price for the video game and the markdown rate are known:

$S$ = $189.99
$d$ = 0.45

Step 2: Calculate the sale price by applying Formula 4.10.

Calculate the markdown amount by applying Formula 4.11b.

Perform:
Step 2:

$S_o_n_s_a_l_e=\char36 189.99\times(1-0.45)$
$=\char36 189.99\times0.55=\char36 104.49$

$D\char36=\char36 189.99-\char36 104.49=\char36 85.50$

Present:
The sale price for the video game is $104.49. When purchased on sale, “Guitar Hero: World Tour” is $85.50 off of its regular price.

Example 4.3B – Markdown Requiring Selling Price Calculation

A reseller acquires an Apple iPad for $650. Expenses are planned at 20% of the cost, and profits are set at 15% of the cost. During a special promotion, the iPad is advertised at $100 off. What is the sale price and markdown percent?

Plan:
The unknown variables for the iPad are the sale price ( $S_o_n_s_a_l_e$ ) and the markdown rate ( $d$ ).

Understand:
Step 1: The pricing elements of the iPad along with the markdown dollars are known:

$C$ = $650
$E = 0.2C$
$P = 0.15C$
$D\char36$ = $100

Calculate the selling price of the product by applying Formula 4.5.

Step 2: Calculate the markdown percent by applying Formula 4.12.

Calculate the sale price by applying Formula 4.11b, rearranging for $S_o_n_s_a_l_e$ .

Perform:
Step 1:

$S=\char36 650+0.2(\char36 650)+0.15(\char36 650)=\char36 877.50$

Step 2:

$d=\frac{\char36 100}{\char36 877.50}\times100=11.396\%$

$\char36 100=\char36 877.50-S_o_n_s_a_l_e$
$S_o_n_s_a_l_e=\char36 777.50$

Present:
When the iPad is advertised at $100 off, it receives an 11.396% markdown and it will retail at a sale price of $777.50.

Never-Ending Sales

Have you noticed that some companies always seem to have the same item on sale all of the time? This is a common marketing practice. Recall the third and fourth circumstances for markdowns. Everybody loves a sale, so markdowns increase sales volumes for both the marked-down product and other regularly priced items.

For example, Michaels has a product line called the Lemax Village Collection, which has seasonal display villages for Christmas, Halloween, and other occasions. When these seasonal product lines come out, Michaels initially prices them at the regular unit selling price for a short period and then reduces their price. For Michaels, this markdown serves a strategic purpose. The company’s weekly flyers advertising the Lemax Village Collection sale attract consumers who usually leave the store with other regularly priced items.

A photo of a portion of an assembled Christmas Lemax Village.

If an item is on sale all the time, then businesses plan the pricing components with the sale price in mind. Companies using this technique determine the unit profitability of the product at the sale price and not the regular selling price. They adapt Formula 4.5 as follows:

$S=C+E+P$
becomes
$S_o_n_s_a_l_e=C+E+P_o_n_s_a_l_e$

where $P_o_n_s_a_l_e$ represents the planned profit amount when the product is sold at the sale price. This is not a new formula, just a new application of Formula 4.5.

How It Works

Under normal circumstances, when businesses set their selling and sale prices they follow a three-step procedure:

Determine the product’s cost, expenses, and profit amount.
Set the regular selling price of the product.
If a markdown is to be applied, determine an appropriate markdown rate or amount and set the sale price.

However, when a product is planned to always be on sale, businesses follow these steps instead to set the sale price and selling price:

Step 1: Set the planned markdown rate or markdown dollars. Determine the pricing components such as cost and expenses. Set the profit so that when the product is marked down, the profit amount is achieved. Alternatively, a planned markup on cost, markup on selling price, or even markup dollars may be set for the sale price.

Step 2: Calculate the sale price of the product. If cost, expenses, and profit are known, apply the adapted version of Formula 4.5. Alternatively, adapt and apply any of the other markup formulas (Formulas 4.6 through 4.9) with the understanding that the result is the sale price of the product and not the regular selling price.

Step 3: Using the known markdown rate or markdown amount, set the regular selling price by applying any appropriate markdown formula (Formulas 4.10 through 4.12).

Assume for the Michael’s Lemax Village Collection that most of the time these products are on sale for 40% off. A particular village item costs $29.99, expenses are $10.00, and a planned profit of $8.00 is achieved at the sale price. Calculate the sale price and the selling price.

Step 1: The known variables at the sale price are

$C$ = $29.99
$E$ = $10.00
$P$ = $8.00
$d$ = 0.40.

Step 2: Adapting Formula 4.5, the sale price is

$S_o_n_s_a_l_e=C+E+P_o_n_s_a_l_e=\char36 29.99+\char36 10.00+\char36 8.00=\char36 47.99$ .

This is the price at which Michael’s plans to sell the product.

Step 3: However, to be on sale there must be a regular selling price. Therefore, if the 40% off results in a price of $47.99, apply Formula 4.10 and rearrange to get the selling price:

$S=\char36 47.99\div(1-0.40)=\char36 79.98$ .

Therefore, the product’s selling price is $79.98, which, always advertised at 40% off, results in a sale price of $47.99. At this sale price, Michael’s earns the planned $8.00 profit.

You may ask, “If the product is always on sale, what is the importance of establishing the regular price?” While this textbook does not seek to explain the law in depth, it is worth mentioning that pricing decisions in Canada are regulated by the Competition Act. With respect to the discussion of never-ending sales, the Act does require that the product be sold at a regular selling price for a reasonable period of time or in reasonable quantity before it can be advertised as a sale price.

If you revisit the Michael’s example, note in the discussion that the village initially needs to be listed at the regular selling price before being lowered to the sale price.

Give It Some Thought:

If a product has a markup on cost of 40% and a markdown of 40%, will it sell above or below cost?
What happens to the profit if a product that is always on sale actually sells at the regular selling price?
Under normal circumstances, arrange from smallest to largest: regular selling price, cost, and sale price.

Example 4.3C – Setting the Price in a Never-Ending Sale

An electronics retailer has 16GB USB sticks on sale at 50% off. It initially priced these USB sticks for a short period of time at regular price, but it planned at the outset to sell them at the sale price. The company plans on earning a profit of 20% of the cost when the product is on sale. The unit cost of the USB stick is $22.21, and expenses are 15% of the cost.
a. At what price will the retailer sell the USB stick when it is on sale?
b. To place the USB stick on sale, it must have a regular selling price. Calculate this price.
c. If the USB stick is purchased at the regular selling price during the initial time period, how much profit is earned?

Plan:
a. This company plans on always having the product on sale, so the pricing needs to be set for the sale price, or $S_o_n_s_a_l_e$ .
b. You need the regular selling price, or $S$ .
c. Solve for the profit at the regular selling price, or $P$ .

Understand:
Step 1: You know the unit cost, the retailer’s associated expenses, its planned profit at the sale price, and the markdown rate:

$d$ = 0.50
$C$ = $22.21
$E$ = 0.15C
$P_o_n_s_a_l_e = 0.2C$

Step 2: To solve part (a), apply the adapted version of Formula 4.5:

$S_o_n_s_a_l_e=C+E+P_o_n_s_a_l_e$

Step 3: After you know the sale price, solve part (b) by applying Formula 4.10, rearranging for $S$ .

Step 4: Solving part (c) requires applying Formula 4.5.

Perform:
Step 2:

$S_o_n_s_a_l_e=\char36 22.21+0.15(\char36 22.21)+0.2(\char36 22.21)$
$=\char36 22.21+\char36 3.33+\char36 4.44=\char36 29.98$

Step 3:

$\char36 29.98=S\times(1-0.5)$
$\char36 29.98=S\times0.5$
$\char36 59.96=S$

Step 4:

$\char36 59.96=\char36 22.21+\char36 3.33+P$
$\char36 59.96=\char36 25.54+P$
$\char36 34.42=P$

Present:
The USB stick is on sale for $29.98, letting the company achieve its profit of $4.44 per unit. During the initial pricing period, the USB stick sells for $59.96 (its regular selling price). If a consumer actually purchases a USB stick during the initial pricing period, the electronics store earns a profit of $34.42 per unit (which is a total of the $4.44 planned profit plus the planned markdown amount of $29.96).

Give It Some Thought Answers

Below cost, since the 40% markdown is off of the selling price, which is a larger value.
The profit will be increased by the markdown amount.
Cost, sale price, regular selling price.

Exercises

Round all money to two decimals and percentages to four decimals for each of the following exercises.

Mechanics

For questions 1–6, solve for the unknown variables (identified with a ?) based on the information provided.

	Regular Selling Price	Markdown Amount	Markdown Percent	Sale Price
1.	$439.85	?	35%	?
2.	?	$100.00	?	$199.95
3.	$1,050.00	?	?	$775.00
4.	$28,775.00	$3,250.00	?	?
5.	?	?	33%	$13,199.95
6.	?	$38.33	12%	?

Applications

7. A pair of Nike athletic shoes is listed at a regular selling price of $89.99. If the shoes go on sale for 40% off, what is the sale price?

8. During its special Bay Days, The Bay advertises a Timex watch for $39.99 with a regular price of $84.99. Calculate the markdown percent and markdown amount.

9. For spring break you are thinking about heading to Tulum, Mexico. In planning ahead, you notice that a one-week stay at the Gran Bahia Principe Tulum, regularly priced at $2,349 for air and six nights all inclusive, offers an early-bird booking discount of $350. What markdown percentage is being offered for booking early?

10. A Heritage Infusio deep frying pan is advertised at 70% off with a sale price of $39.99. What is the frying pan’s regular selling price, and what markdown amount does this represent?

11. A mass merchandiser uses its Lagostina cookware product line as a marketing tool. The cookware is always on sale at an advertised price of 45% off. The cost of the cookware is $199.99, expenses are $75, and the planned profit at the sale price is $110. Calculate the sale price and selling price for the cookware.

12. Quicky Mart regularly sells its Red Bull sports drink for $2.99 per can. Quicky Mart noticed that one of its competitors down the street sells Red Bull for $1.89. What markdown percentage must Quicky Mart advertise if it wants to match its competitor?

13. A hardware store always advertises a Masterdesigner 75-piece screwdriver set at 80% off for a sale price of $17.99.
a. If the cost of the set is $10 and expenses are 30% of the sale price, what is the planned profit when the product is on sale?
b. What profit is earned if the product actually sells at its regular selling price?

14. A campus food outlet is advertising a “Buy one, get one 25% off” deal. The 25% off comes off the lower-priced item. If you purchase a chicken dinner for $8.99 and your friend gets the burger combo for $6.99, what is the markdown percentage on the total price?

15. Blast’em Stereos purchases a stereo system for $1,900 less two discounts of 40% and 18%. The store uses this product to draw customers to the store and always offers the stereo on sale at 25% off. When the stereo is on sale, it plans on expenses equaling 30% of the cost and a profit of 20% of the sale price.
a. What is the sale price for the stereo?
b. How much profit does Blast’em make when the stereo sells at the sale price?
c. By law, this stereo must sell at the regular selling price for a period of time before going on sale. What is the regular selling price?
d. What profit does Blast’em earn if a customer purchases the stereo during this initial period?

Challenge, Critical Thinking, & Other Applications

16. Frigid Boards purchases one of its snowboards for $395 less a retail trade discount of 15% and a loyalty discount of 4%. Its markup on selling price percentage on all snowboards is 21%. At the end of the season, any leftover snowboards are marked down by 10%. What is the sale price for the snowboard?

17. An HP LaserJet printer has an MSRP of $399.95. It is subject to trade discounts of 30% and 23%. The LaserJet is a featured item for a computer store and is always on sale. The store plans to sell the LaserJet for a sale price that allows it to cover expenses equalling 15% of cost and realize a profit of $35.00.
a. What is the sale price?
b. If the MSRP is the regular unit price of the printer, what rate of markdown can the computer store advertise?
c. What markup on selling price percentage is realized at the sale price?

18. The Brick advertises that when you purchase a queen-size Tempur-Pedic mattress set for $2,499.97 it will give you a 51″ 3-D plasma television with a 3-D starter kit included. The value of this gift is $1,199.99. What markdown percent does this represent?

19. A Maytag 27 cubic foot refrigerator retails for $2,400.00 at Landover Appliance Centre. The company, which is celebrating its 30th anniversary this coming weekend, features the fridge for 30% off. The markup on selling price percentage on the fridge at the regular unit selling price is 53%.
a. What is the sale price?
b. At the sale price, what is the markup on selling price percentage?
c. If the expenses are 15% of the regular selling price, what is the profit when the fridge is on sale?

20. Dreger Jewelers is selling a diamond bracelet. It uses this bracelet in its promotions and almost always has it on sale. The cost of the bracelet is $2,135 less discounts of 20% and 30%. When the bracelet is on sale for 25% off, the expenses are 15% of cost and the profit is 20% of cost.
a. What is the sale price?
b. What is the bracelet’s regular selling price?
c. If the bracelet sells at the regular selling price, what are the markup amount and the markup on cost percent?

4.4 Merchandising

Running a business requires you to integrate all of the concepts in this chapter. From discounts to markups and markdowns, all the numbers must fit together for you to earn profits in the long run. It is critical to understand how pricing decisions affect the various financial aspects of your business and to stay on top of your numbers.

Merchandising does not involve difficult concepts, but to do a good job of it you need to keep track of many variables and observe how they relate to one another. Merchandising situations in this section will apply all of the previously discussed pricing concepts. Next, the concept of maintained markup helps you understand the combined effect of markup and markdown decisions on list profitability. Finally, you will see that coupons and rebates influence expenses and profitability in several ways beyond the face value of the discounts offered.

The Complete Pricing Picture

Up to this point, you have examined the various components of merchandising as separate topics. Your study of basic product pricing has included the following:

Taking an MSRP or list price and applying discounts to arrive at a product’s cost.
Marking up a product by adding expenses and profits to the cost to arrive at a regular selling price.
Marking down a product by applying a discount and arriving at a sale price.
Working with various percentages in both markup and markdown situations to either simplify calculations or present a clearer pricing picture.

Now is the time to tie all of these merchandising concepts together. Section 4.2 introduced the concept of a markup chart to understand the relationship between various markup components. The figure below extends this figure to include all of the core elements of merchandising.

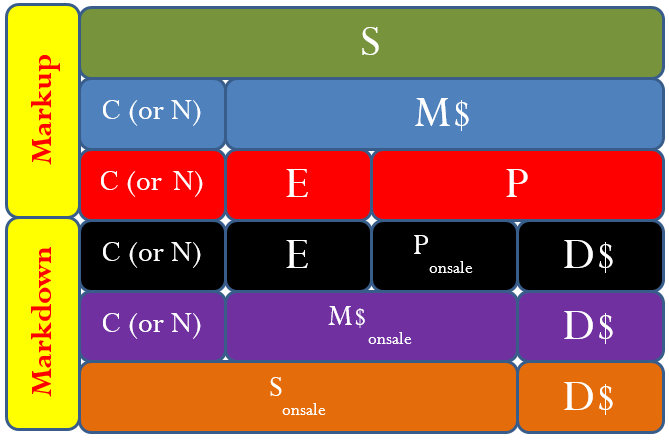
A diagram illustrating the relationships between formulas used to calculate markup and markdown (described below.)

The figure reveals the following characteristics:

You calculate the cost of a product by applying a discount formula. The net price, $N$ , is synonymous with cost, $C$ .
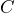When you mark a product down, not only is the profit reduced but the markup dollars are also reduced. The following relationships exist when a product is on sale:

$M\char36_o_n_s_a_l_e=E+P_o_n_s_a_l_e$
OR
$M\char36_o_n_s_a_l_e=M\char36-D\char36$

$P_o_n_s_a_l_e=P-D\char36$

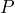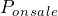At break-even (remember, $P$ or $P_o_n_s_a_l_e$ is zero) a sale product has the following relationships:

$M\char36_o_n_s_a_l_e=E$
$S_o_n_s_a_l_e=C+E$
$D\char36=P$

None of these relationships represent new formulas. Instead, these reflect a deeper understanding of the relationships between the markup and markdown formulas.

How It Works

Follow these steps to solve complete merchandising scenarios:

Step 1: It is critically important to correctly identify both the known and unknown merchandising variables that you are asked to calculate.

Step 2: For each of the unknown variables in step 1, examine Formulas 4.1 through 4.12. Locate which formulas contain the unknown variable. You must solve one of these formulas to arrive at the answer. Based on the information provided, examine these formulas to determine which formula may be solvable. Write out this formula, identifying which components you know and which components remain unknown.

For example, assume that in step 1 you were asked to solve for the expenses, or $E$ . In looking at the formulas, you find this variable appears only in Formulas 4.5 and 4.6, meaning that you must use one of these two formulas to calculate the expenses. Suppose that, in reviewing the known variables from step 1, you already have the markup amount and the profit. In this case, Formula 4.6 would be the right formula to calculate expenses with.

Step 3: Note the unknown variables among all the formulas written in step 2. Are there common unknown variables among these formulas? These common variables are critical variables. Solving for these common unknowns is the key to completing the question. Note that these unknown variables may not directly point to the information you were requested to calculate, and they do not resolve the merchandising scenario in and of themselves. However, without these variables you cannot solve the scenario.

For example, perhaps in step 1 you were requested to calculate both the markup on cost percent ( $MoC\%$ ) and the markup on selling price percent ( $MoS\%$ ). In step 2, noting that these variables are found only in Formulas 4.8 and 4.9, you wrote them down. Examination of these formulas revealed that you know the cost and selling price variables. However, in both formulas the markup dollars remain unknown. Therefore, markup dollars is the critical unknown variable. You must solve for markup dollars using Formula 4.7, which will then allow you to calculate the markup percentages.

Step 4: Apply any of the merchandising formulas from Formulas 4.1 to 4.12 to calculate the unknown variables required to solve the formulas. Your goal is to identify all required variables and then solve the original unknown variables from step 1.

Before proceeding, take a few moments to review the various concepts and formulas covered earlier in this chapter. A critical and difficult skill is now at hand. As evident in steps 2 through 4 of the solving process, you must use your problem-solving skills to figure out which formulas to use and in what order. Here are three suggestions to help you on your way:

Analyze the question systematically. Conscientiously use the Plan, Understand, Perform, and Present model.
If you are unsure of how the pieces of the puzzle fit together, try substituting your known variables into the various formulas. You are looking for
a. Any solvable formulas with only one unknown variable or
b. Any pair of formulas with the same two unknowns, since you can solve this system using your algebraic skills of solving two linear equations with two unknowns (covered in Chapter 1).
Merchandising has multiple steps. Think through the process. When you solve one equation for an unknown variable, determine how knowing that variable affects your ability to solve another formula. As mentioned in step 3, there is usually a critical unknown variable. Once you determine the value of this variable, a domino effect allows you to solve any other remaining formulas.

Example 4.4A – A Merchandising Situation

A skateboard shop stocks a Tony Hawk Birdhouse Premium Complete Skateboard. The MSRP for this board is $82. If the shop is going to stock the board, it must order at least 25 units. The known information is as follows:

The supplier offers a retail trade discount of 37% with a quantity discount of 12% for orders that exceed 15 units.
Typical expenses associated with selling this premium skateboard amount to 31% of the regular selling price.
The skateboard shop wants each of its products to have profitability of 13% of the regular selling price.
In the event that the skateboards do not sell by the end of the season, the skateboard shop always holds an end-of-season clearance sale where it marks down its products to the break-even selling price.

Using this information about the skateboard, determine the following:
a. Cost
b. Regular unit selling price
c. Markup on cost percentage
d. Markup on selling price percentage
e. Sale price
f. Markdown percentage

Plan:
In order, you are looking for $C$ , $S$ , $MoC\%$ , $MoS\%$ , $S_o_n_s_a_l_e$ , and $d(markdown)$ .

Understand:
Step 1: The list price, two discounts (note the store qualifies for both since it meets the minimum quantity criteria), expense and profit information, as well as information on the sale price are known:

$L$ = $82.00
$d_1$ = 0.37
$d_2$ = 0.12
$E$ = 0.31S
$P$ = 0.13S
$S_o_n_s_a_l_e$ = break-even price

The unknown variables are $C$ , $S$ , $MoC\%$ , $MoS\%$ , $S_o_n_s_a_l_e$ , and $d(markdown)$ .

Step 2:
a. Cost and net price are synonymous. Net price appears in Formulas 4.1, 4.2b, and 4.3. Since you know list price and two discounts, calculate cost through Formula 4.3.
b. Selling price appears in Formulas 4.5, 4.7, 4.9, 4.10, 4.11a, and 4.11b. Known variables include expenses and profit. You will know the cost once you have solved part (a). Choose Formula 4.5.
c. Markup on cost percent appears only in Formula 4.8. You will know the cost once you have solved part (a). $M\char36$ is an unknown variable.
d. Markup on selling price percent appears only in Formula 4.9. You will know the selling price once you have solved parts (a) and (b). $M\char36$ is an unknown variable.
e. A break-even price uses an adapted Formula 4.5. You will know the cost once you have solved part (a) and determined the expenses based on the selling price in part (b).
f. Markdown percent appears in Formulas 4.10, 4.11a, and 4.12. You will know the regular price once you have solved part (b). You will know the sale price once you have solved part (e). Choose Formula 4.12.

Step 3:
From the above rationalization, the only unknown variables are cost and markup dollars. Once you know these two variables you can complete all other formulas. Calculate cost as described in step 2a. To calculate markup dollars, use Formulas 4.6, 4.7, 4.8, and 4.9. Once you know the cost and selling price from parts 2(a) and 2(b), you can apply Formula 4.7, rearranging for markup dollars.

Perform:
Calculator Instructions:
For part (d) only, use 2nd Profit

CST

SEL

MAR

45.46

81.18

Answer: 44

a.

$C=N=\char36 82\times(1-0.37)\times(1-0.12)=\char36 45.46$

b.

$S=\char36 45.46+0.31S+0.13S$
$0.56S=\char36 45.46$
$S=\char36 81.18$

c. As determined in step 3, you need markup dollars first.

$\char36 81.18=\char36 45.46+M\char36$
$\char36 35.72=M\char36$

Now solve:

$MoC\%=\frac{\char36 35.72}{\char36 45.46}\times100=78.5746\%$

d.

$MoS\%=\frac{\char36 35.72}{\char36 81.18}\times100=44\%$

e.

$S_o_n_s_a_l_e=S_B_E=\char36 45.46+0.31(\char36 81.18)=\char36 70.63$

f.

$\char36 70.63=\char36 81.18\times(1-d)$
$0.87=1-d$
$0.13=d$

Present:
The cost of the skateboard is $45.46. The regular selling price for the skateboard is $81.18. This is a markup on cost percent of 78.5746% and a markup on selling price percent of 44%. To clear out the skateboards, the sale price is $70.63, representing a markdown of 13%.

Maintained Markup

A price change results in a markup change. Whenever a selling price is reduced to a sale price, it has been demonstrated that the amount of the markup decreases (from $M\char36$ to $M\char36_o_n_s_a_l_e$ ) by the amount of the discount ( $D$ ). This means that some of the products are sold at full markup and some at a partial markup. For businesses, the strategic marking up of a product must factor in the reality that they do not sell every product at the same level of markup. Therefore, if a business must achieve a specified level of markup on its products, it must set its price such that the average of all markups realized equals its markup objective. The average markup that is realized in selling a product at different price points is known as the maintained markup.

To understand the formula, assume a company has 100 units for sale. From past experience, it knows that 90% of the products sell for full price and 10% sell at a sale price because of discounts, damaged goods, and so on. At full price, the product has a markup of $10, and 90 units are sold at this level, equalling a total markup of $900. On sale, the product is discounted $5, resulting in a markup of $5 with 10 units sold, equalling a total markup of $50. The combined total markup is $950. Therefore, the maintained markup is $950 ÷ 100 = $9.50 per unit. If the company’s goal is to achieve a $10 maintained markup, this pricing structure will not accomplish that goal. Formula 4.13 summarizes the calculations involved with maintained markup.

Formula 4.13 – Maintained Markup

$MM=\frac{M\char36(n_1)+(M\char36-D\char36)(n_2)}{n_1+n_2}$

$MM$ is Maintained Markup: The maintained markup is the average markup in dollars that is realized after factoring in the quantity of units sold and differing levels of markup. In its simplest form, this formula is an applied version of Formula 2.4 on weighted average discussed in Chapter 2.

$M\char36$ is Markup Amount: The markup amount represents the amount of markup realized at the regular selling price for the product. If you do not know this amount directly, calculate it using any of the markup formula (Formulas 4.6 through 4.9).

$n_1$ is Full Markup Output: This variable represents the number of units sold at full markup (the regular selling price). It could be an actual or forecasted number of units sold. This variable acts as a weight: If you do not know actual unit information, then you can instead assign a forecasted weight or percentage.

$n_2$ is Partial Markup Output: This variable represents the number of units sold at the reduced markup (the sale price). If you do not know unit information, use a forecasted weight or percentage instead.

$D\char36$ is Markdown Amount: The markdown amount represents the amount by which the regular selling price has been reduced to arrive at the sale price. If you do not know this amount directly, calculate it using any of the markdown formulas (Formulas 4.11a, 4.11b, or 4.12).

Formula 4.13 assumes that only one price reduction applies, implying that there is only one regular price and one sale price. In the event that a product has more than one sale price, you can expand the formula to include more terms in the numerator. To expand the formula for each additional sale price required:

Extend the numerator by adding another 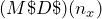$(M\char36 − D\char36)(n_x)$ , where the 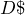$D\char36$ always represents the total difference between the selling price and the corresponding sale price and 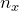$n_x$ is the quantity of units sold at that level of markup.
Extend the denominator by adding another 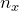$n_x$ as needed.

For example, if you had the regular selling price and two different sale prices, Formula 4.13 appears as:

$MM=\frac{M\char36(n_1)+(M\char36-D\char36_1)(n_2)+(M\char36-D\char36_2)(n_3)}{n_1+n_2+n_3}$

How It Works

Follow these steps to calculate the maintained markup:

Step 1: Identify information about the merchandising scenario. You must either know markup dollars at each pricing level or identify all merchandising information such as costs, expenses, profits, and markdown information. Additionally, you must know the number of units sold at each price level. If unit information is not available, you will identify a weighting based on percentages.

Step 2: If step 1 already identifies the markup dollars and discount dollars, skip this step. Otherwise, you must use any combination of merchandising formulas (Formulas 4.1 to 4.12) to calculate markup dollars and discount dollars.

Step 3: Calculate maintained markup by applying Formula 4.13.

Give It Some Thought:

1. A company’s pricing objective is to maintain a markup of $5. It knows that some of the products sell at regular price and some of the products sell at a sale price. When setting the regular selling price, will the markup amount be more than, equal to, or less than $5?

Example 4.4B – What Level of Markup Is Maintained?

A grocery store purchases a 10 kg bag of flour for $3.99 and resells it for $8.99. Occasionally the bag of flour is on sale for $6.99. For every 1,000 units sold, 850 are estimated to sell at the regular price and 150 at the sale price. What is the maintained markup on the flour?

Plan:
You are looking to calculate the maintained markup ( $MM$ ).

Understand:
Step 1: The cost, selling price, and sale price information along with the units sold at each price are known:

$C$ = $3.99
$S$ = $8.99
$S_o_n_s_a_l_e$ = $6.99
$n_1$ = 850
$n_2$ = 150

Step 2: To calculate markup dollars, apply Formula 4.7, rearranging for $M$ . To calculate markdown dollars, apply Formula 4.11b.

Step 3: Calculate maintained markup by applying Formula 4.13.

Perform:
Step 2:
Markup amount:

$\char36 8.99=\char36 3.99+C$
$C=\char36 5.00$

Markdown amount:

$D\char36 =\char36 8.99-\char36 6.99=\char36 2.00$

Step 3:

$MM=\frac{\char36 5(850)+(\char36 5-\char36 2)(150)}{850+150}=\char36 4.70$

Present:
On average, the grocery store will maintain a $4.70 markup on the flour.

Example 4.4C – Setting Prices to Achieve the Maintained Markup

Maplewood Golf Club has set a pricing objective to maintain a markup of $41.50 on all 18-hole golf and cart rentals. The cost of providing the golf and rental is $10. Every day, golfers before 3 p.m. pay full price while “twilight” golfers after 3 p.m. receive a discounted price equalling $30 off. Typically, 25% of the club’s golfers are “twilight” golfers. What regular price and sale price should the club set to meet its pricing objective?

Plan:
The golf club needs to calculate the regular selling price ( $S$ ) and the sale price ( $S_o_n_s_a_l_e$ ).

Understand:

Step 1: The cost information along with the maintained markup, markdown amount, and weighting of customers in each price category are known:

$C$ = $10
$MM$ = $41.50
$D\char36$ = $30
$n_1=100\%-25\%=75\%$
$n_2=25\%$

Reverse steps 2 and 3 since you must solve Formula 4.13 first and use this information to calculate the selling price and sale price.

Step 3: Apply Formula 4.13, rearranging for $M\char36$ .

Step 2: Calculate the selling price by applying Formula 4.7.

Calculate the sale price by applying Formula 4.11b, rearranging for $S_o_n_s_a_l_e$ .

Perform:
Step 3:

$\char36 41.50=\frac{M\char36(0.75)+(M\char36-30)(0.25)}{0.75+0.25}$
$\char36 41.50=0.75M\char36+0.25M\char36-\char36 7.50$
$\char36 49=M\char36$

Step 2:

$S=\char36 10+\char36 49=\char36 59$

$\char36 30=\char36 59-S_o_n_s_a_l_e$
$S_o_n_s_a_l_e=\char36 29$

Present:
In order to achieve its pricing objective, Maplewood Golf Club should set a regular price of $59 and a “twilight” sale price of $29.

The Pricing Impact of Coupons and Mail-in Rebates

Consumers sometimes need a nudge to help them decide on a purchase. Have you ever been thinking about buying a product but put it off for a variety of reasons? Then, while browsing online one day, you suddenly come across a coupon. You print it off and hurry down to your local store, because the coupon expires in the next few days. You just participated in a price adjustment.

A marketing price adjustment is any marketing activity executed by a member of the distribution channel for the purpose of altering a product’s price. This includes an alteration to the regular unit selling price or a sale price. For example, Sony could distribute a rebate giving its consumers $50 off the price of one of its televisions. Alternatively, Superstore could run a special promotion where customers receive $30 off if they purchase at least $250 in merchandise.

When making price adjustments, businesses must understand the full impact on the bottom line. Many inexperienced businesses distribute coupons for $1 off, assuming that the only cost to be accounted for is the $1. This is untrue for most price adjustments.

These marketing price adjustments reduce the prices that you pay as a consumer. Certainly, some price adjustments are more advantageous than others. Although they come in many types, this section focuses on two of the most widely used price adjustments: manufacturer coupons and mail-in rebates.

Manufacturer Coupons

A coupon is a promotion that entitles a consumer to receive a certain benefit, most commonly in the form of a price reduction. Coupons are typically offered by manufacturers to consumers.

The decision of a manufacturer to issue a coupon affects the expenses associated with the product in three ways.

Coupon Redemption Expense. The coupon redemption expense is the dollar amount price reduction that the coupon offers, also known as the face value of the coupon. The manufacturer must pay out this amount to the reseller as a reimbursement for redeeming the coupon, increasing the expenses accordingly. For example, if a coupon is for $3 off, then the coupon redemption expense is $3.
Coupon Handling Expense. Most commonly, retailers are the resellers that redeem manufacturer coupons. The resulting coupon handling expense for the manufacturer is known as a handling fee or handling charge, payable to the retailer. The manufacturer offers financial compensation to the retailer for redeeming the coupon, filling out the paperwork, and submitting it to manufacturer for reimbursement. Ultimately, the retailer should not be out any money for participating in the promotion. For example, in the small print a coupon may indicate that there is a $0.09 handling fee. This amount is payable to the retailer upon the manufacturer’s receipt of the redeemed coupon.
Coupon Marketing Expense. Coupons do not just magically appear in consumer hands. Companies must pay for the creation, distribution, and redemption of the coupons, which is known as the coupon marketing expense:

- Coupons are designed, turned into print-ready artwork, and printed. This incurs design, labour, and material costs.
- Coupons are commonly distributed separately from the product in media such as magazines, flyers, and newspapers. This requires the purchase of ad space.
- Coupons are commonly redeemed through coupon clearinghouses that handle coupon redemption requests. Manufacturers must pay the fees charged by the clearinghouse.

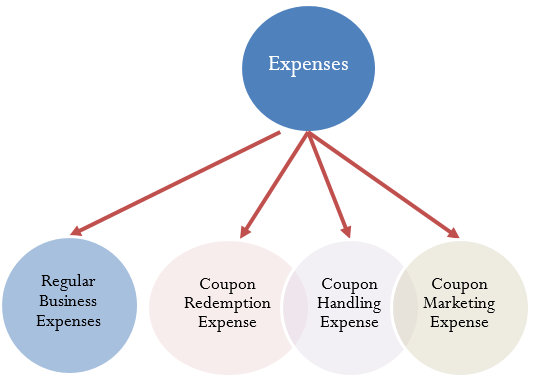
A diagram illustrating the components of coupon expenses: regular business expenses, the coupon redemption expense, the coupon handling expense, and the coupon marketing expense.

The manufacturer issuing the coupon estimates how many coupons it expects consumers will redeem and assigns the average of the coupon marketing costs to each unit based on the forecasted volume.

It should be evident that the decision to issue coupons results in expenses much higher than the face value of the coupon. All three of the expenses listed above are added to the product’s regular expenses. The end result is that the unit expenses increase while unit profits decrease.

As a consumer, you can appreciate the immediacy of the price reduction a coupon offers you at the cash register. Unlike with mail-in rebates, there is nothing further you need to do.

Mail-In Rebates

Have you ever purchased an item that came with a mail-in rebate but not submitted the rebate because it was too much hassle? Was your rebate refused because you failed to meet the stringent requirements? If you answered yes to either of these questions, then you have joined the ranks of many other consumers. In fact, marketers know you will either not mail in your rebates (some estimates are that 50% to 98% of mail-in rebates go unredeemed), or you will fail to send the required supporting materials. From a pricing point of view, this means that more product is sold at the regular price! That is why marketers use mail-in rebates.

Mail-in rebates are similar to coupons; however, there is a distinct difference in how the price adjustment works. A mail-in rebate is a refund at a later date after the purchase has already been made, whereas coupons instantly reward consumers with a price reduction at the cash register. Mail-in rebates commonly require consumers to fill in an information card as well as meet a set of stringent requirements (such as cutting out UPC codes and providing original receipts) that must be mailed in to the manufacturer at the consumer’s expense (see the photo for an example). After a handling time of perhaps 8 to 12 weeks and if the consumer has met all requirements, the manufacturer issues a cheque in the amount of the rebate and sends it to the consumer.

With coupons there are three associated expenses: coupon redemption, handling, and marketing. In the case of rebates, since the participants in the channel are not involved with the rebate redemption, no handling expenses are paid out to the retailers.

Rebate Redemption Expense. The rebate redemption expense is the dollar amount price reduction that the rebate offers, also known as the face value of the rebate. This amount must be paid out to the consumer, commonly in the form of a cheque. For example, if a rebate is for $50, then this is the amount sent to the consumer. This increases expenses, but often not by the full $50. Recall that though many consumers purchase the product because the rebate is offered, not all of them redeem the rebate. To calculate the unit expense many companies average the rebate redemption amount based on the number of rebates they expect to fulfill. Take, for example, a company that issues a $50 rebate on the purchase of a surround sound system. From past experience, it knows that only 5% of the rebates are actually redeemed properly and thus paid out. Therefore, the increase in expenses is not $50, but 5% of $50, or $2.50 per unit sold under the rebate program.
Rebate Marketing Expense. Many mail-in rebates today are distributed either on or in the packaging of the product, or they can be located online. This tends to minimize (but not eliminate) the marketing expenses associated with creation, distribution, and redemption. The rebate marketing expense is commonly averaged across the increase in sales that results from the rebate issuance and not the number or rebates redeemed. Therefore, if a company has $100,000 in rebate marketing expenses, a direct increase in sales by 20,000 units, and only 1,000 rebates redeemed, the rebate marketing expense is $100,000 ÷ 20,000 = $5.00 per unit under the rebate program (note that the rebates redeemed is irrelevant to this calculation).

A diagram illustrating the components of mail-in rebate expenses: regular business expenses, the rebate redemption expense, and the rebate marketing expense.

With coupons and rebates, the focus is on how these marketing tools affect expenses and profit. You do not require any new formula; instead, Formula 4.5 is adapted to reflect the pricing impact of these tactics.

Formula 4.5: The Selling Price of a Product Under a Coupon or Rebate:

$S=C+E(adjusted)+P_o_n_s_a_l_e$

$S$ is Selling Price: The manufacturer’s regular selling price of the product is unchanged for both rebates and coupons. Mail-in rebates do not change the manufacturer’s selling price to the wholesaler. Coupons lower the retail price and not the manufacturer’s price.

$C$ is Cost: The cost of the product to the manufacturer remains constant when marketers use coupons and rebates.

$E(adjusted)$ is Expenses: When coupons and mail-in rebates are used, the manufacturer not only incurs regular operating expenses but must adjust this number upward to reflect the redemption, handling, and marketing expenses associated with these price adjustments. Therefore, products sold under a coupon program or rebate program always have higher expenses.

$P_o_n_s_a_l_e$ is Profit: If the price and cost remain unchanged while the expenses have increased, then the profit per unit must be reduced. Using a coupon or rebate is essentially another form of putting the product on sale. You know that if a product is on sale, then the profits are reduced. The amount of this reduction will be equal to the amount by which the expenses increase.

How It Works

Follow these steps to calculate the selling price or any of its components when working with coupons or rebates:

Step 1: Identify the known components involved in the selling price, such as the cost, unit expense, profit, or selling price. Use any formulas needed to calculate any of these components. Also identify information about the coupon or rebate, including redemption, handling, and marketing expenses.

Step 2: Calculate the unit expense associated with the marketing pricing tactic.

Coupons. The unit redemption expense is equal to the face value of the coupon. The unit handling expense is the promised handling fee of the coupon. The unit marketing expense is a simple average of the total marketing expense divided by the expected number of coupon redemptions. Calculate the total coupon expenses by summing all three elements.
Rebates. The unit redemption expense is equal to the face value of the coupon multiplied by the redemption rate of the rebate. The unit marketing expense is equal to a simple average of the total marketing expense divided by the expected increase in sales as a result of the rebate. Calculate the total rebate expenses by summing both elements.

Step 3: Apply the required merchandising formulas to calculate the unknown variable(s). The modified Formula 4.5 presented earlier will most likely play prominently in these calculations.

Quick Coupon Example

Assume a manufacturer coupon is issued with a face value of $5. The handling charge is $0.15 per coupon. The marketing expenses are estimated at $150,000, and the company forecasts that 100,000 coupons will be redeemed. The regular profit on the product is $20. How much will the unit expenses of the product increase, and what is the unit profit under the coupon program?

Step 1: You know the following information:

$P$ = $20
Face Value = $5
Handling Charge = $0.15
Total Marketing Expenses = $150,000
Forecasted Coupon Redemption = 100,000.

Step 2: The increase in expenses is a sum of the redemption, handling, and marketing expenses. The redemption expense is $5. The handling expense is $0.15. To get the marketing expense per unit, take the total expense and divide it by the number of redemptions expected. Therefore $\char36 150,000\div100,000=\char36 1.50$ .

The total increase in expenses is then $\char36 5.00+\char36 0.15+\char36 1.50=\char36 6.65$ .

Step 3: If the expenses rise by $6.65 with the same cost and selling price, then the profits fall by the same amount.

The unit profit on any product sold using the coupon is $\char36 20.00-\char36 6.65=\char36 13.35$ .

Quick Rebate Example

Assume a manufacturer mail-in rebate is issued with a face value of $20. The marketing expenses are estimated at $300,000 and the company plans on 10% of the mail-in rebates being redeemed. It is forecasted that sales will rise by 37,500 units as a result of the mail-in rebate. The regular profit on the product is $25. How much will the unit expenses of the product increase, and what is the unit profit under the rebate program?

Step 1: You know the following information:

$P$ = $25
Face Value = $20
Total Marketing Expenses = $300,000
Rebate Redemption Rate = 10%
Increase in Sales = 37,500.

Step 2: The increase in expenses is a sum of the redemption and marketing expenses. The redemption expense is $20.00 multiplied by the 10% redemption rate, or $2. To calculate the marketing expense per unit, take the total expense and divide it by the increase in sales. Therefore $\char36 300,000\div37.500=\char36 8$ .

The total increase in expenses is then $\char36 2+\char36 8=\char36 10$ .

Step 3: If the expenses rise by $10 with the same cost and selling price, then the profits fall by the same amount. The unit profit on any product sold using the coupon is $\char36 25-\char36 10=\char36 15$ .

When calculating the per-unit expense, be careful to distinguish how to handle the various associated expenses for both manufacturer coupons and mail-in rebates, as summarized in the table below.

Marketing Tactic

Redemption Expense

Handling Expense

Marketing Expense

Coupon

Face value of the coupon

A flat rate per coupon

The total expense divided by the number of coupons redeemed

Mail-In Rebate

Face value of the mail-in rebate multiplied by the redemption rate

N/A

The total expense divided by the increase in sales attributed to the mail-in rebate

It pays to be smart when you deal with coupons and mail-in rebates as a consumer. Two important considerations are timing and hassle.

Timing. Coupon amounts are usually smaller than rebate amounts. You may be offered a $35 coupon (sometimes called an “instant rebate,” but should not be confused with rebates) at the cash register, or a $50 mail-in rebate. If you choose the former, you get the price savings immediately. If you choose the latter, you must spend the money up front and then wait 8 to 12 weeks (or more) to receive your rebate cheque.
Hassle. Mail-in rebates are subject to very strict rules for redemption. Most require original proofs of purchase such as your original cash register receipts, UPC codes, model numbers, and serial numbers (which are difficult to find sometimes). You must photocopy these for your records in the event there is a rebate problem. Specific dates of purchase and deadlines for redemption must be met. Some rebates, particularly computer software upgrades, even require you to send your old CD-ROM in with your purchase, substantially raising your postage and envelope costs. Does all that extra time and cost justify the rebate? For example, Benylin ran a sales promotion offering an instant coupon for $1; alternatively you could purchase two products and mail-in two UPC codes for a $3 rebate. When factoring in costs for postage, envelope, photocopying, and time, the benefit from the mail-in rebate is marginal at best.

Give It Some Thought:

2. What happens to the unit profit when a coupon or rebate is issued under the following scenarios?
a. The cost and selling price remain unchanged.
b. The cost increases and the selling price remains unchanged.
c. The cost remains the same and the selling price is reduced.
d. The cost remains the same and the selling price increases.

Example 4.4D – The Impact of a Coupon

When the DVD edition of the Bee Movie was released in retail stores, DreamWorks Animation executed a coupon marketing program. Assume the unit cost of the DVD is $2.50, the normal expenses associated with the DVD amount to $1.25, and that DreamWorks sells it directly to retailers for $10. The coupon offered a $3 savings on the DVD to consumers and promised the retailer an $0.08 handling fee per coupon redeemed. The estimated costs of creating, distributing, and redeeming the coupons are $285,000, and the projected number of coupons redeemed is 300,000.
a. What is the unit profit of the DVD when it sold without the coupon?
b. What unit profit did DreamWorks realize for those DVDs sold under its coupon promotion?

Plan:
You need to first calculate the profit ( $P$ ) when no coupon was available. Second, you will calculate the impact of the coupon on the profit when the DVD is discounted under the coupon program ( $P_o_n_s_a_l_e$ ).

Understand:
Step 1: The unit cost of the DVD along with its normal associated expenses and regular unit selling price are known. The coupon details are:

$C$ = $2.50
$E$ = $1.25
$S$ = $10.00
Face Value = $3
Handling Fee = $0.08
Total Marketing Expense = $285,000
Number of Redeemed Coupons = 300,000

Step 2: When the coupon is issued, the expenses associated with the DVD rise to accommodate the coupon redemption expense, the handling expense, and the marketing expenses.

Step 3: Calculate the profit normally realized on the DVD by applying Formula 4.5, rearranging for $P$ .

Recalculate the profit under the coupon program by adapting Formula 4.5, rearranging for $P_o_n_s_a_l_e$ .

Perform:
Step 2:
Unit coupon expense = $\char36 3+\char36 0.08+(\char36 285,000\div300,000)=\char36 4.03$

Step 3:

$\char36 10.00=\char36 2.50+\char36 1.25+P$
$\char36 6.25=P$

$\char36 10.00=\char36 2.50+(\char36 1.25+\char36 4.03)+P_o_n_s_a_l_e$
$\char36 10.00=\char36 7.78+P_o_n_s_a_l_e$
$\char36 2.22=P_o_n_s_a_l_e$

Present:
Without the coupon promotion a Bee Movie DVD generates $6.25 in profit. Under the coupon promotion, DreamWorks achieves a reduced profit per DVD of $2.22.

Example 4.4E: The Impact of a Mail-In Rebate

Computer manufacturers commonly issue rebates on items such as printers and monitors. Assume LG decided to distribute its new 22” widescreen LCD monitor (MSRP: $329.99) with a prepackaged mail-in rebate included inside the box. The rebate is $75. The company predicts a 25% rebate redemption rate. Its unit cost to produce the monitor is $133.75, with expenses equalling 35% of cost. It sells the monitor directly to retailers for a regular unit selling price of $225. The increased marketing expenses for promotion and rebate redemption equal $8.20 per monitor. What is the profit for a monitor sold through the rebate program?

Plan:
You are looking for the profit ( $P_o_n_s_a_l_e$ ) for a monitor sold under the rebate program. This profit must factor in the rebate face value, redemption rate, and marketing expenses.

Understand:
Step 1: The unit cost, unit expenses, and regular unit selling price are known. The rebate details are:

$C$ = $133.75
$E = 0.35C$
$S$ = $225.00
Face Value = $75
Redemption rate = 25%
Unit Marketing Expenses = $8.20

Step 2: When the rebate is issued, the expenses associated with the monitor rise to accommodate the rebate redemption expenses and the marketing expenses.

Step 3: Apply an adjusted Formula 4.5, rearranging for $P_o_n_s_a_l_e$ .

Perform:
Step 2: Unit rebate expense = $\char36 75\times25\%+\char36 8.20=\char36 18.75+\char36 8.20=\char36 26.95$

Step 3:

$\char36 225.00=\char36 133.75+(\char36 46.81+\char36 26.95)+P_o_n_s_a_l_e$
$\char36 225.00=\char36 207.51+P_o_n_s_a_l_e$
$\char36 17.49=P_o_n_s_a_l_e$

Present:
The rebate redemption expense for the LG monitor is $18.75. LG averages a profit of $17.49 per monitor sold under its mail-in rebate program.

Give It Some Thought Answers

1. More than $5. In order to average to $5, the markup at regular price must be higher than $5 and the markup at sale price must be lower than $5.

2. a.Profit decreases by the total unit expenses associated with the coupon or rebate.
b. Profit decreases by the sum of the total unit expenses associated with the coupon or rebate and the amount of the increased cost together.
c. Profit decreases by the sum of the total unit expenses associated with the coupon or rebate and increases by the amount of the price increase.
d. Profit decreases by the total unit expenses associated with the coupon or rebate and the amount of the increased cost together.

Exercises

Round all money to two decimals and percentages to four decimals for each of the following exercises.

Mechanics

For questions 1–4, solve for the unknown variables (identified with a ?) based on the information provided.

Regular Unit Selling Price

Cost

Unit Expenses

Profit

Markup Amount

Break-Even Price

Markup on Cost

Markup on Selling Price

Markdown Amount

Markdown Percent

Sale Price

1.

$100.00

?

24% of $C$

?

100%

50%

?

33%

?

2.

?

$20.00

$30.00

?

$13.00

?

$37.00

3.

?

$56.25

?

10% of $S$

?

33.3333%

?

$64.99

4.

$99.99

$43.00

?

$78.50

?

13%

?

10%

?

For questions 5–8, solve for the unknown variables (identified with a ?) based on the information provided. N/A indicates that the particular variable is not applicable in the question.

	Regular Unit Selling Price	Unit Cost	Regular Unit Expenses	Coupon or Rebate Handling Expense per Unit	Coupon or Rebate Redemption Expense per Unit	Coupon or Rebate Marketing Expense per Unit	Profit w/o Coupon or Rebate per Unit	Profit with Coupon or Rebate per Unit
5.	$9.85	$4.73	35% of $C$	$0.25	$2.00	$0.75	?	?
6.	$47.65	$23.50	15% of $S$	N/A	$10.00	$3.50	?	?
7.	$6.30	?	$0.95	$0.45	?	$1.15	$3.05	$0.45
8.	?	$38.25	40% of $C$	N/A	?	$2.25	$21.40	$4.15

Applications

9. A box of glossy inkjet photo paper costs $9.50. The markup on cost is 110%. The profit is 31.5% of the cost. The paper occasionally goes on sale for 20% off.
a. What are the regular unit selling price, expenses, profit, markup amount, and markup on selling price percentage?
b. When the paper goes on sale, what are the sale price, markdown amount, markup dollars, and markup on selling price percentage?

10. John’s Bakery is thinking of distributing a $0.50 coupon for one of its least popular brands of bread in hopes of increasing its sales. The bread costs $0.43 to produce, and expenses are 10% of the regular unit selling price. The bread retails for $1.99 per loaf. John’s Bakery estimates that the coupon marketing expenses are $0.25 per loaf sold, and coupon handling expenses would be an additional $0.10 per loaf sold.
a. What is John’s Bakery profit when the loaf is sold at the regular unit selling price without the coupon?
b. If John’s Bakery uses the coupon, what is the profit?
c. If the bread still doesn’t sell well, John’s Bakery will clear it out while still allowing consumers to use the coupon. What is the break-even selling price for a loaf in this situation?

11. An airline needs to maintain an average markup of $230 on a daily return flight from Toronto to Vancouver. The Boeing 737-800 has a capacity of 166 passengers, and the cost per passenger is $175. Typically 90% of tickets are sold at full fare while 10% are sold on standby at a sale price equalling $200 off the regular price. What regular and sale prices should the airline set to maintain the average markup?

12. A mail-in rebate form is printed on the side of every High Liner box of breaded fish. It allows the consumer to mail in the UPC along with the form and receive a $2 rebate. If a 700 g box of fish is normally sold to grocery stores for $3.50, costs are 40% of the regular unit selling price, and expenses are 20% of cost, what is the expected profit under the rebate program? Assume that only 25% of rebates are actually redeemed and that rebate marketing expenses are $0.15 per box.

13. Lay’s Potato Chips is thinking of distributing a coupon on its 454 g bag of regular crinkled chips. Currently, the cost of producing a bag of chips is $0.49, with typical expenses of $0.23 per bag. Lay’s sells the bag to retailers for $1.75 per bag. The coupon is in the amount of $0.50, while retailers are offered $0.12 for handling expenses. Lay’s forecasts an increase in sales of 300,000 bags with the coupon, incurring total marketing expenses of $100,000. Will running this coupon promotion be profitable for Lay’s? What is its profit (or loss) per unit if Lay’s goes forward with the coupon?

14. LG is thinking of placing a $30 mail-in rebate on its 19” widescreen computer monitor. The cost to produce a monitor is $67.40, with typical expenses amounting to 50% of the cost. The monitor is sold to retailers for $119.00. Based on previous rebate programs, LG knows that only 40% of those who purchased a monitor with a rebate will actually redeem it. The marketing expense associated with the rebate totals $350,000, resulting in increased sales of 50,000 monitors. Is the rebate program profitable for LG? What is its profit (or loss) per monitor if it proceeds with the rebate offer?

15. A car dealership acquired a used Ford Mustang for $15,000. Its expenses on used vehicles are 15% of the cost, and it prices the vehicle with a 30% markup on cost percentage. After two months, if the car doesn’t sell, it marks the car down by 10%.
a. What are the expenses?
b. What is the dollar amount of the markup?
c. What is the regular selling price?
d. What is the markup on selling price percentage?
e. What is the sale price?
f. What is the amount of the markdown?
g. What is the profit earned if the car is sold at the sale price?
h. What is the maintained markup supposing the dealership was able to acquire eight used Ford Mustangs at the same cost, where five cars are sold at regular price and three are sold at the sale price?

Challenge, Critical Thinking, & Other Applications

16. Target is trying to determine whether it would be more profitable to use a coupon or a mail-in rebate when promoting a new supersoaker water gun. The toy costs $14.94 and retails for $29.95. Expenses are 30% of cost. The coupon is for $4, handling expenses are $0.50 per unit, and the marketing expenses are $1 per unit. The rebate is for $7.75, with 45% of the rebate forms expected to be redeemed. Rebate marketing expenses are $1.25 per unit.
a. If Target forecasts that sales will increase 10,000 units under the coupon program and 8,000 units under the rebate program, should it use the coupon or the mail-in rebate?
b. How much more profit is earned based on your recommended option?

17. A hair salon has limited shelf space to carry shampoo products. The store’s pricing policies have a markup on cost of 220%, and expenses equal 20% of cost. Two suppliers have approached the salon with the following offers:
Supplier #1: The shampoo has a list price of $29 with discounts of 60% and 20%. Over a six-month period, 150 bottles are expected to be sold at full price and 50 bottles at a 25% markdown during a special promotion.
Supplier #2: The shampoo has a list price of $37 with discounts of 70% and 10%. Over a six-month period, 120 bottles are expected to be sold at full price and 75 bottles at a 20% markdown during a special promotion.
Based on this information, recommend which supplier the salon should purchase the shampoo from. Show calculations to support your answer.

18. The Home Depot purchases garden sheds for $1,000 less discounts of 40% and 20% and then sells them at a 100% markup on cost percentage. Seasonally, these sheds sell for full price initially followed by a reduced price and then are blown out at 50% off the regular price. Past experience indicates that 60% of the sheds sell at full price, 30% at the reduced price, and 10% at the blowout price. What should the reduced price be set at to achieve a maintained markup of $360?

19. CCM sells ice skates to Sport Chek for $179.99 less a trade discount of 40% and a quantity discount of 15%. The ice skates cost $27.60 to manufacture, and associated expenses are 35% of the regular unit selling price. CCM runs a mail-in rebate program on the ice skates where consumers receive $50 on a pair of skates. CCM estimates that 40% of purchasers will redeem the rebate. Rebate marketing expenses are estimated at $6 per pair sold. What is CCM’s profitability under the rebate program?

20. Canadian Tire purchases a camping tent from its supplier at an MSRP of $79.99 less discounts of 40% and 25%. It plans to sell the tent at the MSRP, and its expenses are 20% of the selling price. At the end of the season, remaining tents are sold at 30% off.
a.What are the expenses?
b. What is the profit?
c. What is the dollar amount of the markup?
d. What is the markup on selling price percentage?
e. What is the markup on cost percentage?
f. What is the sale price?
g. What is the amount of the markdown?
h. What is the profit earned when tents are sold at the sale price?
i. What is the maintained markup if 90% of tents are sold at the regular price and 10% of tents are sold at the sale price?

Key Takeaways

Section 4.1: Figuring Out the Cost: Discounts (How Much?)

The relationship between distribution and pricing
Some of the types of discounts available to businesses and consumers
How to calculate the net price when only one discount is involved
How to calculate the net price when multiple discounts are involved
Converting multiple discounts into single discounts

Section 4.2: Markup: Setting the Regular Price (Need to Stay in Business)

The three components that compose a selling price
Calculating the markup in dollars and the relationship to pricing components
Calculating the markup as a percentage under two different approaches
Determining the price point where all costs are paid but no profits are earned—the break-even point

Section 4.3: Markdown: Setting the Sale Price (Everybody Loves a Sale)

How to take a regular selling price and make it into a sale price by applying markdowns
How to plan the merchandising of products that are always on sale
Section 4.4: Merchandising (How Does It All Come Together?)
Combining discounts, markup, and markdown into complete merchandising situations
Calculating the maintained markup when a product was sold at both a regular selling price and a sale price
How coupons and mail-in rebates impact product pricing

Section 4.4: Merchandising (How Does It All Come Together?)

Combining discounts, markup, and markdown into complete merchandising situations
Calculating the maintained markup when a product was sold at both a regular selling price and a sale price
How coupons and mail-in rebates impact product pricing

The Formulas You Need to Know

Symbols Used

$C$ = cost

$d$ = discount rate or markdown rate

$d_1$ , $d_2$ , … $d_n$ = multiple discount rates, where the subscript represents each discount up to a count of n discounts

$D\char36$ = discount amount or markdown amount

$E$ = expenses

$L$ = list price

$M\char36$ = markup amount

$MM$ = maintained markup

$MoC\%$ = markup on cost percentage

$MoS\%$ = markup on selling price percentage

$n$ = number of pieces of data, which in this chapter is the level of output

$N$ = net price

$P$ = profit

$P_o_n_s_a_l_e$ = planned profit amount when a product is sold at the sale price

$S$ = regular selling price

$S_B_E$ = the selling price at the break-even point

$S_o_n_s_a_l_e$ = sale price

Formulas Introduced

Formula 4.1 Single Discount: $N= L\times(1-d)$ (Section 4.1)

Formula 4.2a Discount Amount: $D\char36=L\times d$ (Section 4.1)

Formula 4.2b Discount Amount: $D\char36=L-N$ (Section 4.1)

Formula 4.3 Multiple Discounts: $N=L\times(1-d_1)\times(1-d_2)\times\cdots\times(1-d_n)$ (Section 4.1)

Formula 4.4 Single Equivalent Discount: $d_e_q_u_i_v=1-(1-d_1)\times(1-d_2)\times\cdots\times(1-d_n)$ (Section 4.1)

Markup Formulas

Formula 4.5 The Selling Price of a Product: $S=C+E+P$ (Section 4.2)

Formula 4.6 Markup Amount: $M\char36 =E+P$ (Section 4.2)

Formula 4.7 The Selling Price of a Product Using the Markup Amount: $S=C+M\char36$ (Section 4.2)

Formula 4.8 Markup on Cost Percentage: $MoC\%=\frac{M\char36}{C}\times100$ (Section 4.2)

Formula 4.9 Markup on Selling Price Percentage: $MoS\%=\frac{M\char36}{S}\times100$ (Section 4.2)

Formula 4.13 Maintained Markup: $MM=\frac{M\char36(n_1)+(M\char36-D\char36)(n_2)}{n_1+n_2}$ (Section 4.4)

Markdown Formulas

Formula 4.10 The Sale Price of a Product: $S_o_n_s_a_l_e=S\times(1-d)$ (Section 4.3)

Formula 4.11a Markdown Amount: $D\char36=S\times d$ (Section 4.3)

Formula 4.11b Markdown Amount: $D\char36=S-S_o_n_s_a_l_e$ (Section 4.3)

Formula 4.12 Markdown Percentage: $d=\frac{D\char36}{S}\times100$ (Section 4.3)

Technology

Calculator

The following calculator functions were introduced in this chapter:

Markup on Selling Price Percentage

2nd Profit to access this feature.

Enter two of the three variables by pressing Enter after each input and using ↑ and ↓ to scroll through the display. The variables are:

CST = The cost of the item

SEL = The selling price of the item

MAR = The markup on selling price percentage (in % format)

Press CPT on the unknown (when it is on the screen display) to compute.

Chapter 4 Review Exercises

Round all money to two decimals and percentages to four decimals for each of the following exercises.

Mechanics

1. The Gap is purchasing an Eminem graphic T-shirt for its stores. If the list price for the T-shirt is $34.50 and the Gap can receive a 40% trade discount, what net price will the Gap pay?

2. Nike has been approached by a retailer who wants to carry their Shox brand. The retailer needs a trade discount of 30% and its wholesaler needs 15%. The retailer also wants a 5% quantity discount. If the MSRP for the shoes is $195.00, what is the wholesale (net) price that Nike will charge?

3. If the regular price of a product is $775.00 and it is eligible to receive discounts of 14%, 8%, and 5%, what single discount percentage is equal to the multiple discount percentages? Show calculations that show how the single and multiple discounts produce the same net price.

4. Subway wants to price a new 12 inch sandwich. The cost of all the ingredients is $1.23. Expenses are 200% of cost, and Subway wants to earn a profit of 187% of cost. What is the regular selling price of the new sandwich?

5. If the cost of a Bose Wave music system is $27.82 and the list price is $49.99, determine the markup amount. Express the markup both as a percentage of cost and percentage of selling price.

6. Rogers Communications is thinking about having a special promotion on its Digital One Rate 250 Plan, which offers 250 minutes of cellular calling. If the current price is $85.00 per month and Rogers wants to put it on special for $75.00 per month, what is the percentage markdown?

7. If a $1 coupon is distributed for a product that normally has a profit of $4 per unit, how much is the profitability reduced if coupon handling expenses are $0.30 per unit and coupon marketing expenses are $1.10 per unit? What is the profit under the coupon program?

8. At a local retailer, a swimsuit costs $10 and sells for $30. At the end of the season, the swimsuit price is reduced by 30%. If 820 swimsuits are sold at the regular price and 145 swimsuits are sold at the sale price, what is the maintained markup?

Applications

9. An iMac has an MSRP of $774.99 with available trade discounts of 20% to the retailer and an additional 15% to the wholesaler.
a. What price should a retailer pay for the product? What is the dollar value of the discount?
b. What price should a wholesaler pay for the product? How much less than the retailer’s price is this?
c. Overall, what single discount percent does the wholesaler receive?

10. The marketing manager for Tim Hortons is attempting to price a cup of coffee. She knows that the cost of the coffee is $0.14 per cup, and expenses are 30% of the regular selling price. She would like the coffee to achieve an 88.24% markup on selling price.
a. What is the regular selling price for a cup of coffee?
b. What is the profit per cup?
c. What is the markup on cost percentage?

11. A grocery store head office is thinking of distributing a $3 in-store coupon for one of its 454 g bags of coffee. The cost of the coffee to one of the franchised retail stores is $6.34, and it is usually sold to consumers for $12.99. A retail store incurs expenses of 25% of the regular selling price to stock, shelve, and sell the coffee. The franchisees are reimbursed $0.25 per coupon redeemed for handling expenses, and the head office estimates that it incurs marketing expenses amounting to $1.35 per coupon. Based strictly on the profit associated with the sale of this coffee, should the head office proceed with this promotion?

12. Jonathan needs a new business suit for a presentation in his communications course. He heads to Moores and finds a suit on sale for 33% off. The regular price of the suit is $199.50.
a. What is the sale price?
b. What is the dollar amount of the markdown?

13. Birchwood Honda needs to clear out its Honda generators for an end-of-season sale. If the dealership pays $319.00, has expenses of 15% of cost, and profits of 30% of the regular unit selling price, what markdown percentage can the dealership advertise if it wants to break even during the sale?

14. eMachines has decided to issue a $50 mail-in rebate on one of its best-selling desktop computers. Retailers purchase the machines directly from eMachines for a list price of $449.00 less a 40% trade discount. eMachines has profits of 35% of its regular unit selling price and expenses of 20% of its regular unit selling price.
a. What is the profit per computer during the rebate, assuming rebate marketing expenses of $13.50 per unit and an expected redemption rate of 35%?
b. How much lower is the profit with the rebate than without the rebate?
c. If 2,500 computers are sold at regular price and 1,025 computers are sold through the rebate program, what is the maintained markup?

Challenge, Critical Thinking, & Other Applications

15. A retailer purchasing the Halo 3 video game is eligible to receive a trade discount, quantity discount, and loyalty discount. If the net price of the game is $22.94, the list price is $39.99, the trade discount is 25%, and the quantity discount is 15%, what percentage is the loyalty discount?

16. An article in a business paper on October 22, 2008, reported that the benchmark S&P/TSX Composite Index ended down 558.92 points for the day, or 5.7%. It went on further to state that the index is down 30% for the year 2008. Rounding all point values to two decimals, answer the following:
a. What were the point values on October 21 and 22, respectively?
b. What was the point value at the start of the year 2008?

17. Whistler Blackcomb Ski Resort purchased 400 pairs of skis for sale in its retail store. It sells the skis at an MSRP of $299.99. It is eligible to receive discounts of 35% and 20% on its purchase. Expenses average 15% of cost. If it sells 300 pairs of skis at the regular unit selling price and the other 100 skis are sold during a clearance sale for 20% off, what is the total amount of profit that Whistler Blackcomb earns? What is the maintained markup?

18. A company is examining its options for selling a product listed at $359.97. Both expenses and profits are 20% and 22% of the regular unit selling price, respectively. At this price, the company forecasts sales of 6,000 units. Consider the following two scenarios:
Scenario A: If the company holds a sale and marks down the product by 10%, its market research predicts that sales will rise to 11,225 units.
Scenario B: If the company issues a $60.00 mail-in rebate, it will have increased marketing expenses of $6.35 per unit. Only 45% of rebates are expected to be redeemed. Market research predicts that sales will rise to 10,500 units.
Should the company leave the product at its regular price, conduct the sale, or issue the mail-in rebate?

19. Indigo is stocking a new hardcover book. The book has a cover price of $44.99 and Indigo is eligible to receive discounts of 25%, 8%, 4%, and 1%. Expenses are 20% of cost. The book sells for the cover price.
a. What is the profit per book?
b. Some new books are launched at 30% off the cover price. From a strictly financial perspective, would it be wise for Indigo to use this approach for this book? Why or why not?

20. Mary is shopping for a new George Foreman grill. While shopping at Polo Park Shopping Centre, she came across the following offers at three different retail stores:
Offer #1: Regular price $149.99, on sale for 30% off.
Offer #2: Regular price $169.99, on sale for 15% off plus an additional 30% off.
Offer #3: Regular price $144.95, on sale for 10% off plus an additional 15% off. Mary also gets a 5% loyalty discount at this store.
Which is the best offer for Mary?

Chapter 4 Case Study: Making a Profitable Product Selection

The Situation

Lightning Wholesale is looking at changing its ski product line for 2014. It wants to carry only two brands of skis. It has received four offers from four different ski manufacturers. The details of the offers are in the first table. It will select the two brands that offer the highest total profit. The accounting department has analyzed 2013 sales and provided the income statement summarized in the second table, which specifies the percentage of each category that is attributed to the sporting goods department.

The Data

	Nordica	Fischer	Ogasaka	Atomic
List Price:	$799.95	$914.99	$829.95	$839.99
Discounts:
Retail	40%	40%	40%	40%
Wholesale	5%	11%	6%	7%
Seasonal	3%	5%
Sale	5%		5%	10%
Loyalty	3%		5%
Quantity	3%	4%	5%	2%

Lightning Wholesale Income Statement

	Year (2013)	Allocation of Dollars to Sporting Goods
Sales Revenue:	$57,77
	7	20%
Cost of Goods Sold:	$50,44
	5	19%
Operating Expenses:
Sales and Marketing	$3,234	18%
General and Administrative	$348	14%
Payroll	$1,416	19%
Total Operating Expenses:	$4,998
Operating Income:	$2,334

*All dollar figures are in thousands

Important Information

All of Lightning Wholesale’s retail customers plan to sell the skis at the list price.
Lightning Wholesale prices all of its skis on the assumption that all of its retailers use the standard industry markup of 40% of the regular selling price.
Skis fall into the sporting goods category for Lightning Wholesale.
Expenses are assigned to products based on the percentage of cost method for each category.
Forecasted sales for each brand (if carried by Lightning Wholesale) in 2014 are as follows:
Nordica = 380 units
Fischer = 270 units
Ogasaka = 310 units
Atomic = 300 units

Your Tasks

Based strictly on financial considerations, recommend which two brands Lightning Wholesale should carry in 2014.
a. Using the appropriate table, calculate the net price (cost) of each brand of skis.
b. To determine the expenses for each brand of skis:
Using the appropriate table, calculate the dollar values assigned to sporting goods for each row by multiplying the company total by the allocation percentage.
Total the dollar amount of the expenses.
Convert the total expenses into a percentage of cost.
Calculate the expenses for each brand using the percentage of cost.
c. Using the appropriate table, calculate the wholesale price (the amount at which Lightning Wholesale will sell the skis to a retailer).
d. For each brand, calculate the profit per unit.
Calculate the total profitability for each brand.
At the end of the year, if any inventories are left over, Lightning Wholesale clears out all ski products at break-even.
a. Determine the break-even prices for the two recommended brands.
b. Determine the markdown percentage that can be advertised for each recommended brand.

Chapter 4: Marketing Applications (answers to section exercises)

4.1 Discounts

D$ = $411.60; N = $568.40
L = $800; D$ = $200
d = 42.625%; N = $1,133.16; D$ = $841.84
d = 26.7904%; L=$500; D$ =$133.95
$259.97
$24.32
31.985%
$19.99
d = 43.972%; L = $51.76
L =\ 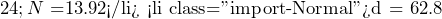$24; N = $13.92</li> <li class="import-Normal">d = 62.8%; L = $700; D$ = $439.60
d = 26%; N = $303.99; D$ = $96</li> <li class="import-Normal">$1,026</li> <li class="import-Normal">d = 63.14%; N = $29.49</li> <li class="import-Normal">$1,194,553.06</li> <li class="import-Normal">2 years 216 days</li> <li class="import-Normal">Reduced by 17.4154%</li> <li class="import-Normal">a. 3%, b. $2.50</li> <li class="import-Normal">a. 52.2328%; b. $3,073.82</li> <li class="import-Normal">a. $74.99; b. $60.91; c. L = $78.74; N = $63.96; D$ =$14.78</li> </ol> <ul> <li> <h3>4.2 Markup</h3> </li> </ul> <ol> <li class="import-Normal"> S=$321.95; SBE =$236.95; M$=$133.53; MoC%=70.8683%; MoS%=41.4754%</li> <li class="import-Normal">C=$653.59; SBE =$849.67; M$=$346.41; MoC%=53.0011%; MoS%=34.6413%</li> <li class="import-Normal">C=$118.25; S=$301.53; E=$153.13; MoS%=60.7833%; SBE =$271.38</li> <li class="import-Normal">M$=$96.25; P=$41.25; C=$178.74; SBE =$223.74</li> <li class="import-Normal">C=$744.83; S=$1,284.83; P=$204.83; MoC%=72.5%; MoS%=42.0289%</li> <li class="import-Normal">M$=81.60; S=$201.60; E=$51.36; MoS%=40.4762%; SBE =$171.36</li> <li class="import-Normal">P=$175; S=$1,447.37; C=$1,172.37; MoC%=23.4568%; SBE =$1,272.37</li> <li class="import-Normal">C=$220; S=$287.50; M$=$67.50; MoS%=23.4783%; MoC%=30.6818%</li> <li class="import-Normal">$112.50</li> <li class="import-Normal">125%</li> <li class="import-Normal">$27,996.79</li> <li class="import-Normal">$57.05</li> <li class="import-Normal">a. $733.03; b. $219.91; c. 53.3151%; d. $698.03</li> <li class="import-Normal">a. $119.95; b. $40.85; c. 51.6435%; d. 34.0559%; e. 28.8887%</li> <li class="import-Normal">$20.82</li> <li class="import-Normal">$102.40</li> <li class="import-Normal">42.8571%</li> <li class="import-Normal">$488.09</li> <li class="import-Normal">a. $40.47; b. $21.79; c. $62.26; d. $14.51; e. $12.20; $2.31 reduction</li> <li class="import-Normal">a. $12.65; b. $17.71; c. $0.63; d. MoS% = 28.5714%; e. C = $15.18; S = $21.25; P = $0.76; MoS% = 28.5647%</li> </ol> <ul> <li> <h3>4.3 Markdown</h3> </li> </ul> <ol> <li class="import-Normal"> D$=$153.95; Sonsale=$285.90</li> <li class="import-Normal">S = $299.95; d = 33.3389%</li> <li class="import-Normal">D$ = $275; d = 26.1905%</li> <li class="import-Normal">Sonsale =$25,525; d=11.2945%</li> <li class="import-Normal">S = $19,701.42; D$ = $6,501.47</li> <li>S=$319.42; Sonsale =$281.09</li> <li>Sonsale = $53.99</li> <li>D$ = $45; d = 52.9474%</li> <li>d = 14.9%</li> <li>S = $133.30; D$ = $93.31</li> <li>Sonsale = $384.99; S=$699.98</li> <li>d = 36.7893</li> <li>a.Ponsale =$2.59; b. P = $74.55;</li> <li>d = 10.9512%</li> <li>a.Sonsale =$1,519.05; b. Ponsale =$303.81; c. S = $2,025.40; d. P = $810.16</li> <li>Sonsale =$367.20</li> <li>a.Sonsale= $282.91; b. d = 29.2637%; c. MoS% = 23.8026%</li> <li>D = 32.4325%</li> <li>Sonsale =$1,680; b. MoS% when on sale = 32.8571%; c. Ponsale =$192.0</li> <li>a. Sonsale =$1,614.06; b. S = $2,152.08; c. M$ = $956.48; MoC% = 80%</li> </ol> <ul> <li> <h3>4.4 Merchandising</h3> </li> </ul> <ol> <li class="import-Normal"> M$=$50; C=$50; P=$38; SBE = $62; D$ = $33; Sonsale =$67</li> <li class="import-Normal">S = $50; C = $20; E = $10; SBE = $30; MoC% = 150%; MoS% = 60%; d = 26%</li> <li class="import-Normal">M$ = $18.75; S = $75; E = $11.25; SBE = $67.50; MoS% = 25%; D$ = $10.01; d= 13.346̅%</li> <li class="import-Normal">E =$35.50; M$ = $56.99; P = $21.49; MoC% = 132.5348%; D$ =$10; Sonsale =$89.99</li> <li class="import-Normal">P=$3.46; Ponsale =$0.46</li> <li>P=$17;Ponsale =$3.50</li> <li>C = $2.30; Coupon Redemption = $1</li> <li>S = $74.95; Rebate Redemption =\$ 15
a. M$ = $10.45; S = $19.95; P = $2.99; E = $7.46; MoS% = 52.381%, 9b. Sonsale=$15.96; D$=$3.99; M$_onsale =$6.46; MoS%_onsale =40.4762%
a. P = $1.36; b. P_onsale =$0.51; c. SBE = $1.48
S=$425;S_onsale =$225
P_onsale =$1.17
P_onsale =$0.08; The promotion is profitable and generates a total profit of $0.08 × 300,000 =$24,000
P_onsale =-$1.10; The promotion is not profitable and generates a loss of $1.10 × 50,000 =$55,000
a.E = $2,250; b. M$ = $4,500; c. S = $19,500; d. MoS% = 23.0769%; e. Sonsale=$17,550; f. D$ = $1,950; g. P_onsale =$250; h. MM = $3,768.75
a. Use the coupon; b. Increase in profit = $3,980
Choose Supplier 2 since $75.85 more profit is earned.
S_onsale =$720
P_onsale =$6.06
a. E = $16.00; b. P = $27.99; c. M$ = $43.99; d. MoS% = 54.9944%, e. MoC% = 122.1944%, f. S_onsale =$55.99; g. D$ =$24.00; h. P_onsale =$3.99; i. MM = $41.59

Statistics Canada, “Failure Rates for New Firms,” The Daily, February 16, 2000, www.statcan.gc.ca/daily-quotidien/000216/dq000216b-eng.htm. ↵
Competition Bureau, Fair Business Practices Branch, Price Scanning Report, Table B, page 5, 1999, www.competitionbureau.gc.ca/epic/site/cb-bc.nsf/en/01288e.html. ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

BUSI1915 - Fundamentals of Business Mathematics Copyright © by OER Lab is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

4.1 Discounts

How Distribution and Pricing Work

Types of Discounts

Single Discounts

Multiple Discounts

Give It Some Thought Answers

Mechanics

Applications

Challenge, Critical Thinking, & Other Applications

4.2 Markup

The Components in a Selling Price

Calculating the Markup Dollars

Calculating the Markup Percent

Break-Even Pricing

How It Works

Give It Some Thought Answers

Mechanics

Applications

Challenge, Critical Thinking, & Other Applications

4.3 Markdown

The Importance of Markdowns

Never-Ending Sales

How It Works

Give It Some Thought Answers

Mechanics

Applications

Challenge, Critical Thinking, & Other Applications

4.4 Merchandising

The Complete Pricing Picture

Maintained Markup

The Pricing Impact of Coupons and Mail-in Rebates

Manufacturer Coupons

Mail-In Rebates

How It Works

Give It Some Thought Answers

Mechanics

Applications

Challenge, Critical Thinking, & Other Applications

The Formulas You Need to Know

Symbols Used

Formulas Introduced

Markup Formulas

Markdown Formulas

Technology

Calculator

Mechanics

Applications

Challenge, Critical Thinking, & Other Applications

Chapter 4 Case Study: Making a Profitable Product Selection

The Situation

The Data

Important Information

Your Tasks

4.1 Discounts

License

Share This Book