Part 7 – Power in AC Circuits

Power

True Power

The power (watts) that is actually used in the circuit. Power is associated with the total resistance in the circuit. The actual power that is converted into another form of energy by the circuit is measured with a wattmeter.

Calculated using the following formula:

    \Huge \begin{align*} P \text{ watts} &= I^2R \\ &= \frac{E^2}{R} \end{align*}

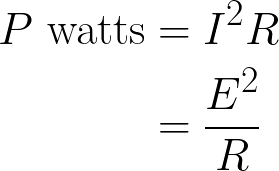
Where:

  • P = True Power (Watts)
  • I = Resistive Current (Amperes)
  • R = Resistance (Ohms)
  • E = Circuit Voltage (volts)

Reactive Power

Reactive power does not produce an energy conversion in the circuit. It is measured in Volt-Amperes Reactive (vars). The reactive loads such as inductors and capacitors dissipate zero power because they drop voltage and draw current giving the impression that they actually do dissipate power.

Reactive power is calculated using the following formula:

    \Huge \begin{align*} Q, \text{vars} &= I^2X \\ &= \frac{E^2}{X} \end{align*}

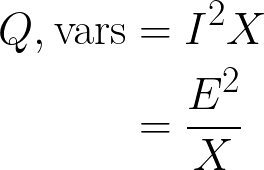
Where:

  • Q = Reactive power (Volt-Amps-Reactive (VAR))
  • I = Impedance (amps)
  • X = Reactance (ohms)
  • E = Circuit Voltage (volts)

Apparent Power

Power that appears to the source because of the circuit’s impedance. It is the power that the voltage sees. When meters are used to measure power in an AC circuit, apparent power is the voltage reading multiplied by the current reading. The combination of true power and reactive power.

Apparent power is calculated using the following formula:

S = I2Z
= E2Z
= IE

Where:

  • S = Apparent power (Volt-amperes (VA))
  • I = Current (amps)
  • Z = Impedance (ohms)

or

Apparent power  =  √((True power)2 + (Reactive power)2)

Power Triangle

A power triangle is a graphical representation used to depict the relationships between real power (measured in watts), reactive power (measured in volt-amperes reactive or VAR), and apparent power (measured in volt-amperes or VA) in an alternating current (AC) circuit. It helps to illustrate how these three quantities are related and how they contribute to the overall power in the circuit.

Power Triangle highlighting apparent power (S) measured in VA, Reactive power (Q) measured in VAR, impedance phase angle and true power (P) measured in watts
Power Triangle

Example:

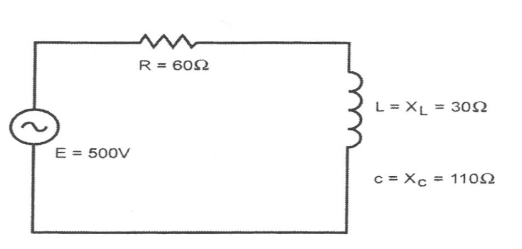
The circuit shown below has a supplied voltage of 500V, resistance of 60 ohms, inductance of 30 ohms, and capacitance of 110 ohms.

Calculate the following:

a) True power
b) Apparent power

Circuit of Resistance, Inductance and Capacitance in Series highlighting R = 60 ohms, E= 500V, L=XL=30ohms, c=Xc=110Ohms
Circuit of Resistance, Inductance, and Capacitance in Series

Solution:

  • R = 60 ohms
  • XL = 30 ohms
  • XC = 110 ohms
  • E = 500 volts

a)  True Power

XT = XC – XL

= 110 – 30

= 80 Ω

Z  = √(R2 + XT2)

= √(602 + 802)

= √(3600 + 6400)

= √(10000)

= 100 Ω

IZ  = E/Z

= 500/100

= 5 A

True Power = I2R

= 52 x 60

= 25 x 60

= 1500 watts

= (5)2 x 100
= 25 x 100
= 2500 VA

Solution

  • R = 60 ohms
  • X = 80 ohms
  • Z = 100 ohms
  • E = 500 volts
  • I = 5 amps

True Power = 1500 watts

b) Apparent Power

Apparent Power = I2Z
= (5)2 x 100
= 25 x 100
= 2500 VA

Alternate Solution:

  • R = 60 ohms
  • X = 80 ohms
  • Z = 100 ohms
  • E = 500 volts
  • I = 5 amps

True Power = 1500 watts

b) Apparent Power

Reactive Power   = I2X

= (5)2 x 80

= 2000 vars

Apparent Power = √((True Power)2 + (Reactive Power)2)

= √((1500)2 + (2000)2)

= √(625 x 104)

= 2500 VA

License

PEG-3722 Electrotechnology Copyright © by Josee Beaulieu. All Rights Reserved.

Share This Book