Part 6 – Transformer Connections

Josee Beaulieu

Part 6 – Transformer Connections

Methods of Connecting a Transformer

There are three identical single-phase transformers that can be connected together to form a three-phase transformer. The voltage/amperage formula for a single-phase transformer is: VA = volts (E) x amperes (I), usually in kVA.

Calculating Current in a Transformer

An example of calculating current in a transformer would be:

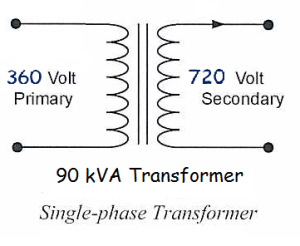
Consider a 360/720 90 kVA transformer. If 360 V is applied to the primary windings, 720 V will be available at the secondary windings.

The secondary current available would be:

$I (secondary) = \frac{90000 VA}{720V}$

$= 125 A$

$I (primary) = \frac{90000 VA}{360V}$

$= 250 A$

A diagram of a 90 kVA single-phase transformer with a 360-volt primary coil and a 720-volt secondary coil.

The voltage/amperage formula for a three-phase transformer is: $VA = \sqrt 3 \times I_L \times E_L$

$I_L = line current$

$E_L = line voltage$

Total capacity of the three single-phase transformers connected in a three-phase arrangement:

$3 \times 90 kVA = 270 kVA$

Connecting a Transformer

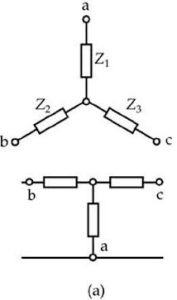
There are two methods of connecting three individual sets of windings in a three-phase transformer, which are the star method and the delta method.

A schematic representation of a star (or wye) connection in a three-phase system with impedance loads Z1, Z2, and Z3.

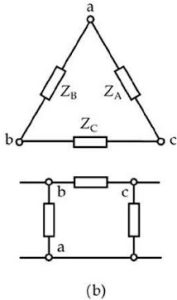Star Connection

Delta Connection

The star (Wye) method is a three-phase line current that is equal to the current in any one phase. The three-phase line voltage is equal to √3 x the voltage in any one phase. The delta method is a three-phase line voltage that is equal to the voltage in any one phase. The three-phase line current is equal to √3 x the current in any one phase.

Three-phase 225 kVA transformer with both primary and secondary windings connected in Delta.

The current is:

$VA = \sqrt 3 \times I_L \times E_L$

$I_L = \frac{VA}{\sqrt 3 \times E_L}$

A delta-delta connection current is:

$I_L (secondary) = \frac{225000 VA}{\sqrt 3 \times 480 V} = 270.6 A$

$I_L (primary) = \frac{225000 VA}{\sqrt 3 \times 240 V} = 541.3 A$

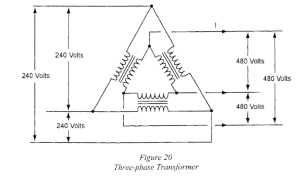A schematic for a three-phase transformer, showing voltage levels and calculations for secondary and primary current (I_t), along with the transformer connections providing 240 volts and 480 volts.

Delta-star connection – star provides two voltages: line voltage = 831 V and phase voltage = 480 V. Current is:

$I_L (secondary) = \frac{225000 VA}{\sqrt 3 \times 831 V} = 156.3 A$

*Uses line voltage

A Step-Down Transformer

Click on the image hotspots to explore the functions of as step-down transformer.

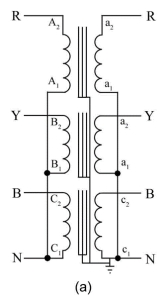
There are only four possible three-phase transformer combinations, which are:

Delta to delta
Delta to star
Star to delta
Star to star

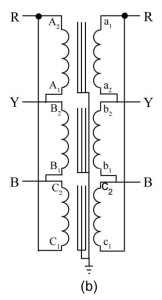A diagram of a three-phase transformer with star-star (wye-wye) connection, illustrating the coils connected in a star configuration on both the primary (R, Y, B) and secondary (a, b, c) sides.

Delta-delta connection

Star-star connection

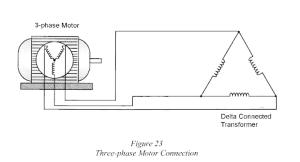
The use of delta or star depends on the application. A delta connection is for balanced loads. A three-phase motor is an example of a balanced load in which each of the windings of the motor has identical impedance. It only requires three supply conductors. A star connection is for unbalanced loads and requires four wires.

Unbalanced Load

Click on the image hotspots to explore the functions of an unbalanced load.

Here is a schematic diagram of a three-phase motor connected to a delta-configured transformer, depicting the electrical connection between them.

A schematic of a three-phase motor connected to a delta-configured transformer, depicting the electrical connection between them.

Part 6 – Transformer Connections

Methods of Connecting a Transformer

Calculating Current in a Transformer

Connecting a Transformer

License

Share This Book