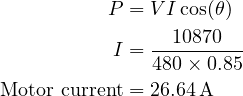Part 6 – Torque and Speed

Motor Speed

Decreasing the field strength of a motor increases its speed by reducing the back electromotive force (EMF), resulting in fewer lines being cut by the armature conductors. This reduction in back EMF leads to more armature current, which, in turn, generates a larger torque, ultimately causing the motor to accelerate.

Increasing the field strength results in a decrease in motor speed due to the increased back electromotive force resulting from more lines being cut by the armature conductors. This, in turn, reduces the armature current flow. The motor will continue to slow down until the counter EMF and armature current stabilize at values that can carry the load at a constant speed.

Activity: Motor Speed

Drag and drop the words in the correct sequence.

Varying field excitation is the most common method used for controlling the speed of shunt and compound motors.  A field rheostat varies the shunt-field current which changes the field flux in turn reducing resistance in the field circuit and causing a decrease in speed. Increasing resistance causes an increase in speed.

The rated armature voltage in North America, for larger DC motors, falls between 250 to 500 VDC. An unloaded motor may run at 1200 RPM with 500 volts applied. The same unloaded motor would run at approximately 600 RPM with 250 volts applied.

The motor’s nameplate provides essential performance data, such as the base speed at rated voltage and the rated full-load amps. Additionally, it indicates that, under a constant field strength, there is a linear relationship between the applied voltage to the armature and the resulting speed.

Motor Full Load Speed

To calculate the full load speed of a motor:

N = \frac{{(V - I_aR_a)}}{{Z\Phi}} \times \frac{{60A}}{{P}}

  • N = Speed of motor, rpm
  • V = supply voltage to motor
  • Ia = Armature current
  • Ra = Resistance
  • Z = Number of armature conductors = Number of conductor slots x number of conductors per slot
  • Φ = Flux/pole
  • A = Number of parallel paths
  • Lap wound = number of poles
  • Wave wound = 2 (regardless of poles)
  • P = Number of Poles

Example:

Calculate the full-load speed of a DC motor operating from a 480 v supply, given:

  • Ra = 0.8 Ω, full load armature current is 60 A, flux/pole is 0.03 Wb. It is a four-pole motor with a simple wave wound armature with 45 slots and 12 conductors per slot.

Solution:

  • N = Speed of motor, rpm
  • V = 480 v
  • Ia = 60 A
  • Ra = 0.8 Ω
  • Z = 45 x 12 = 540 conductors
  • Φ = 0.03 Wb
  • A = Parallel Paths = Wave wound = 2 (regardless of poles)
  • P = 4 poles

To calculate the full load speed of a motor:

(1)   \begin{align*} N &= \frac{{(V - I_aR_a)}}{{Z\Phi}} \times \frac{{60A}}{{P}} \\ &= \frac{{(480 - 60 \times 0.8)}}{{540 \times 0.03}} \times \frac{{60 \times 2}}{4} \\ &= 800 \text{ rpm} \end{align*}

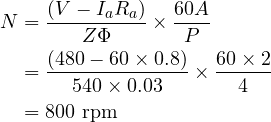
Power Input

Power Input to a motor calculation:

PI = V I cosθ

  • P = Power to motor
  • V = Voltage
  • I = Current
  • cos θ = Power Factor

Calculating Current

To calculate current flow you must convert motor output and input to Watts:

1 kW = 1000 W

  • Motor Output = Motor Input x Efficiency
  • Motor Input (PI) = Motor Output/Efficiency

(2)   \begin{align*} P_I &= VI \cos(\theta) \\ I &= \frac{P}{V \cos(\theta)}\end{align*}

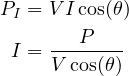
Example:

A 480 V single-phase DC motor is rated at 10 kW and operates at a power factor of 0.85 (lagging), with an efficiency of 92%. Calculate the current taken from the power supply.

Solution:

  • V = 480 volts
  • PF = cos θ = 0.85
  • Efficiency = 92% = 0.92
  • Motor Output = 10 kW = 10 x 1000 W/kW = 10,000 W

(3)   \begin{align*} \text{Motor Input (W)} &= \frac{\text{Motor Output}}{\text{efficiency}} \\ &= \frac{10,000}{0.92} \\ &= 10,870 \, \text{W} \end{align*}

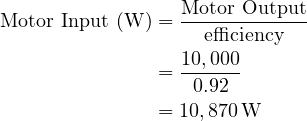
and

(4)   \begin{align*} P &= V I \cos(\theta) \\ I &= \frac{10870}{480 \times 0.85} \\ \text{Motor current} &= 26.64 \, \text{A} \end{align*}

 

License

PEG-3722 Electrotechnology Copyright © by Josee Beaulieu. All Rights Reserved.

Share This Book