Part 2 – AC Sine Wave
AC Theory
Average or Mean Value
Direct current systems supply a constant voltage that does not vary with time.
When Voltage (V) is applied to a resistive load (R), the power (P) consumed is determined by the formula:
P = V2/R

Activity: Sinusoidal Voltage
Click the image hotspots to learn more about sinusoidal voltage.
Peak-to-Peak and RMS Values of AC Systems
Peak to Peak value
The magnitude of the voltage or current measured between the maximum positive value and the maximum negative value.
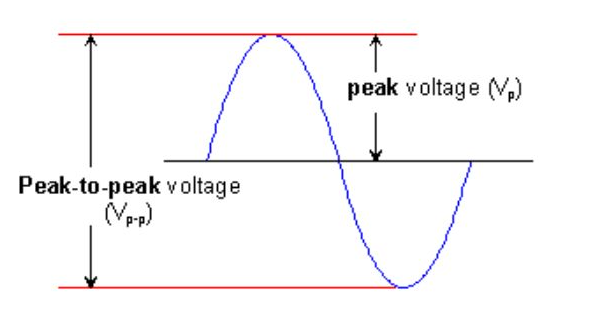
Root-Mean-Square Value (RMS Value)
The equivalent DC voltage that can deliver the same amount of energy to a resistor as the AC does over a cycle is defined as the root-mean-square of a sine wave.
The root-mean-square of a sine wave is:
![Rendered by QuickLaTeX.com \Large \[ \frac{\text{Peak value}}{\sqrt{\frac{1}{2}}} \]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5b5bdbf486dc0fef94bfa0013cd6c5a5_l3.png)
To determine the RMS value, three mathematical operations are carried out on the function representing the AC sine wave:
- The square of the wave is determined.
- The square of the wave from step 1 is averaged over time.
- The square root of the averaged square of the wave from step (2) is calculated.
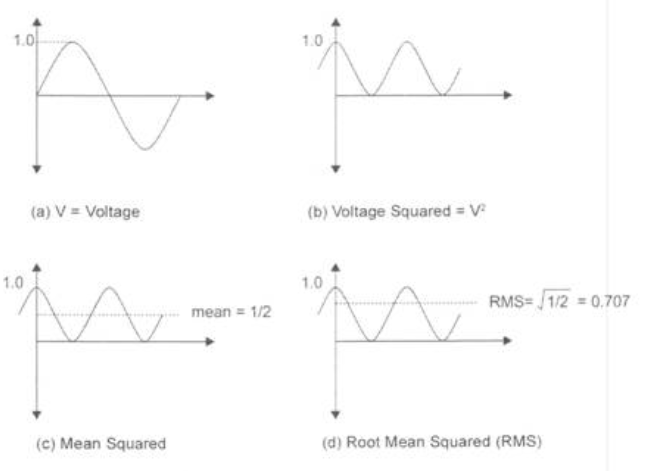
RMS value is necessary for measurement purposes because instantaneous values of alternating current and voltage constantly vary with time between positive and negative values. The average value of alternating current or voltage would be zero.
RMS Voltage
RMS voltage is calculated as follows:
Peak voltage x RMS value (0.707) = RMS voltage
i.e., For normal household voltage
- 120 volts = peak voltage x 0.707
 volts = peak voltage
volts = peak voltage- 170 volts = peak voltage
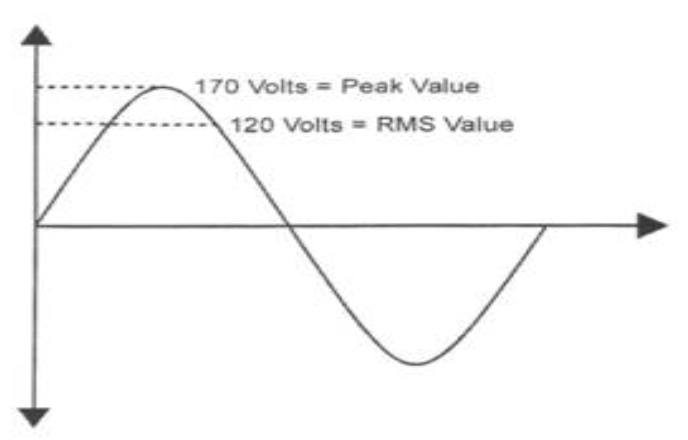
RMS quantities are measured by AC voltmeters and ammeters.
