Part 10 – DC Efficiency

Josee Beaulieu

Part 10 – DC Efficiency

Power Losses

Losses that occur in DC machines are classified as rotational losses and electrical losses.

These losses can be listed as:

Friction
Copper
Iron

Power losses due to friction include:

Bearing friction
Brush friction
Wind friction

Copper loss is due to the resistance in armature and field windings, representing electrical power (I²R) transformed into heat.

Power losses stemming from iron occur as a result of power loss within the magnetic circuit which can be attributed to:

Eddy currents
Hysteresis

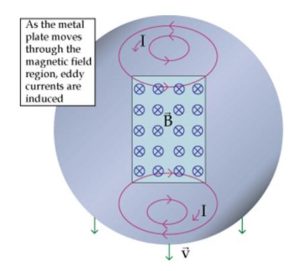
Eddy Current

Eddy currents are currents induced in conductors to oppose the change in flux that generated them. They are caused when a conductor is exposed to a changing magnetic field due to the relative motion of the field source and conductor which causes a circulating flow of electrons, or a current, within the body of the conductor. This is considered a loss.

As the metal plate moves through the magnetic field region, eddy currents are induced

Hysteresis

Hysteresis refers to losses associated with magnetizing and demagnetizing substances such as iron, steel, and associated alloys. It takes energy for a material to be magnetized – the molecular particles are aligned and produce north and south poles.

Heat loss results from the magnetic properties of the armature. When an armature core is exposed to a magnetic field, its magnetic particles align with the field. As the armature core rotates, its magnetic field constantly changes direction, causing the magnetic particles to continually realign. This ongoing movement generates molecular friction, resulting in heat, which is subsequently transmitted to the armature windings. This heat, in turn, leads to an increase in armature resistance.

Efficiency

The efficiency of any machine is given by:

$\text{Efficiency} = \frac{\text{Power Output}}{\text{Power Input}}$

DC motor output can be measured using a calibrated brake or a dynamometer. The input power is measured using electrical instrumentation.

In the case of large generators, the electrical output requires the dissipation of large amounts of heat energy.

Generator Efficiency:

$\text{Efficiency}_{G} = \frac{\text{Power Input}}{\text{Power Input + Losses}}$

Motor Efficiency:

$\text{Efficiency}_{M} = \frac{\text{Power Input - Losses}}{\text{Power Input}}$

Calculating Generator Efficiency

$\text{Efficiency}_{G} = \frac{\text{Power Output}}{\text{Power Input}}$

Losses are copper + iron + friction

$\begin{aligned} \text { Copper Loss } & =\quad \text { Armature Power }\left(\mathrm{P}_{\mathrm{a}}\right)+\text { Field Circuit Power }\left(\mathrm{P}_{\mathrm{f}}\right) \mid \\ & =\quad \text { Armature } \mathrm{I}^2 \mathrm{R}+\text { Field Circuit } \mathrm{I}^2 \mathrm{R} \end{aligned}$

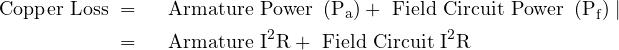
Calculate Generator output current (I_G)

$=\frac{\text { Power Input }}{\text { Voltage }}=\frac{P_t}{E}$

Calculate Field Circuit Current (I_f)

$\begin{aligned} & =\underline{\text { Voltage }} \quad=\quad \underline{E} \\ & \text { Field Resistance } \quad R_f \\ & \end{aligned}$

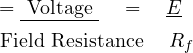
Calculate Armature Current (I_a)

$\begin{aligned} & =\quad \text { Generator Output Current }+ \text { Field Current } \\ & =\quad \mathrm{I}_{\mathrm{G}}+\mathrm{I}_{\mathrm{f}} \end{aligned}$

Armature Power (I²R)

$=\quad \mathrm{I}_{\mathrm{a}}^2 \times \mathrm{R}_{\mathrm{a}} $$$

Field Circuit Power (I²R)

$=\mathrm{I}_{\mathrm{fc}}^2 \times \mathrm{R}_{\mathrm{fc}}$

Total Copper Loss

$\begin{aligned} & =P_{\mathrm{a}}+\mathrm{P}_{\mathrm{fc}} \\ & =\left(\mathrm{I}_{\mathrm{a}}^2 \times \mathrm{R}_{\mathrm{a}}\right)+\left(\mathrm{Ifc}_{\mathrm{fc}}^2 \times \mathrm{R}_{\mathrm{fc}}\right) \end{aligned}$

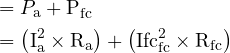
Total losses (Full Load)

= Copper loss + friction loss

Generator Efficiency

$\text { Efficiency }_G=\frac{\text { Power Input }}{\text { Power Input }+ \text { Total Losses }}$

Example:

A shunt generator has the following particulars at full-load rating: output 33 kilowatts, volts 350, armature circuit resistance 0.8 ohms, field circuit resistance 288 ohms; friction and iron losses combined 990 watts. Calculate the generator efficiency at this load.

Solution:

Power P_t = 33 kW = 33,000 W
Power P_fi (frict+iron loss) = 990 W
E = 350 V
R_a (Armature Res.) = 0.8 ohms
R_fc (Field Circuit Res) = 288 ohms

Generator Efficiency = $\frac{\text{output}}{\text{input}}$

Output = Input – Losses

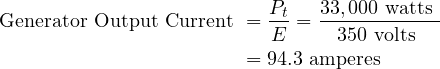
$\begin{aligned} \text { Generator Output Current } & =\frac{P_t}{E}=\frac{33,000 \text { watts }}{350 \text { volts }} \\ & =94.3 \text { amperes } \end{aligned}$