Notes for the TI-83, 83+, 84, 84+ Calculators

 

Quick Tips

Legend

  • A blank calculator button represents a button press
  • [ ] represents yellow command or green letter behind a key
  • < > represents items on the screen

To adjust the contrastPress 2nd key, then hold arrow up to increase the contrast or arrow down to decrease the contrast.

To capitalize letters and wordsPress alpha key to get one capital letter, or press 2nd key, then alpha key to set all button presses to capital letters. You can return to the top-level button values by pressing alpha key again.

To correct a mistakeIf you hit a wrong button, just hit clear key and start again.

To write in scientific notationNumbers in scientific notation are expressed on the TI-83, 83+, 84, and 84+ using E notation, such that…

  • 4.321 E 4 = \text{4}\text{.321}×{\text{10}}^{4}
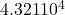
  • 4.321 E –4 = \text{4}\text{.321}×{\text{10}}^{-4}

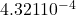
To transfer programs or equations from one calculator to another:Both calculators: Insert your respective end of the link cable cable and press 2nd key, then [LINK].

Calculator receiving information:

  1. Use the arrows to navigate to and select <RECEIVE>
  2. Press enter key.

Calculator sending information:

  1. Press appropriate number or letter.
  2. Use up and down arrows to access the appropriate item.
  3. Press enter key to select item to transfer.
  4. Press right arrow to navigate to and select <TRANSMIT>.
  5. Press enter key.
Note

ERROR 35 LINK generally means that the cables have not been inserted far enough.

Both calculators: Insert your respective end of the link cable cable Both calculators: press 2nd key, then [QUIT] to exit when done.

Manipulating One-Variable Statistics

Note

These directions are for entering data with the built-in statistical program.

Sample Data We are manipulating one-variable statistics.
Data Frequency
–2 10
–1 3
0 4
1 5
3 8

To begin:

  1. Turn on the calculator.
     on key

  2. Access statistics mode.
     stat key

  3. Select <4:ClrList> to clear data from lists, if desired.
    number 4 key , enter key

  4. Enter list [L1] to be cleared.
     2nd key , [L1] , enter key

  5. Display last instruction.
     2nd key , [ENTRY]

  6. Continue clearing remaining lists in the same fashion, if desired.
     arrow left key , 2nd key , [L2] , enter key

  7. Access statistics mode.
     stat key

  8. Select <1:Edit . . .>
     enter key

  9. Enter data. Data values go into [L1]. (You may need to arrow over to [L1]).

    • Type in a data value and enter it. (For negative numbers, use the negate (-) key at the bottom of the keypad).
       negative sign key , number 9 key , enter key

    • Continue in the same manner until all data values are entered.

  10. In [L2], enter the frequencies for each data value in [L1].

    • Type in a frequency and enter it. (If a data value appears only once, the frequency is “1”).
       number 4 key , enter key

    • Continue in the same manner until all data values are entered.

  11. Access statistics mode.
     stat key

  12. Navigate to <CALC>.

  13. Access <1:1-var Stats>.
     enter key

  14. Indicate that the data is in [L1]…
     2nd key , [L1] , comma key

  15. …and indicate that the frequencies are in [L2].
     2nd key , [L2] , enter key

  16. The statistics should be displayed. You may arrow down to get remaining statistics. Repeat as necessary.

Drawing Histograms

Note

We will assume that the data is already entered.

We will construct two histograms with the built-in STATPLOT application. The first way will use the default ZOOM. The second way will involve customizing a new graph.

  1. Access graphing mode.
     2nd key , [STAT PLOT]

  2. Select <1:plot 1> to access plotting – first graph.
     enter key

  3. Use the arrows navigate go to <ON> to turn on Plot 1.
     <ON> , enter key

  4. Use the arrows to go to the histogram picture and select the histogram. enter key
  5. Use the arrows to navigate to <Xlist>.

  6. If “L1” is not selected, select it.
     2nd key , [L1] , enter key

  7. Use the arrows to navigate to <Freq>.

  8. Assign the frequencies to [L2].
     2nd key , [L2] , enter key

  9. Go back to access other graphs.
     2nd key , [STAT PLOT]

  10. Use the arrows to turn off the remaining plots.
  11. Be sure to deselect or clear all equations before graphing.

To deselect equations:

  1. Access the list of equations.
     Y= key

  2. Select each equal sign (=).
     arrow down key arrow right key enter key

  3. Continue, until all equations are deselected.

To clear equations:

  1. Access the list of equations.
     Y= key

  2. Use the arrow keys to navigate to the right of each equal sign (=) and clear them.
     arrow down key arrow right key clear key

  3. Repeat until all equations are deleted.

To draw default histogram:

  1. Access the ZOOM menu.
     ZOOM key

  2. Select <9:ZoomStat>.
     number 9 key

  3. The histogram will show with a window automatically set.

To draw custom histogram:

  1. Access window mode to set the graph parameters.
     window key
    • {X}_{\mathrm{min}}=-2.5
    • {X}_{\mathrm{max}}=3.5
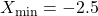
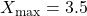
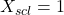    • {X}_{scl}=1 (width of bars)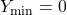
    • {Y}_{\mathrm{min}}=0
    • {Y}_{\mathrm{max}}=10
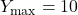
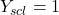    • {Y}_{scl}=1 (spacing of tick marks on y-axis)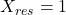
    • {X}_{res}=1
  3. Access graphing mode to see the histogram.
     graph key

To draw box plots:

  1. Access graphing mode.
     2nd key , [STAT PLOT]

  2. Select <1:Plot 1> to access the first graph.
     enter key

  3. Use the arrows to select <ON> and turn on Plot 1.
     enter key

  4. Use the arrows to select the box plot picture and enable it.
     enter key

  5. Use the arrows to navigate to <Xlist>.

  6. If “L1” is not selected, select it.
     2nd key , [L1] , enter key

  7. Use the arrows to navigate to <Freq>.

  8. Indicate that the frequencies are in [L2].
     2nd key , [L2] , enter key

  9. Go back to access other graphs.
     2nd key , [STAT PLOT]

  10. Be sure to deselect or clear all equations before graphing using the method mentioned above.

  11. View the box plot.
     graph key , [STAT PLOT]

Linear Regression

Sample Data

The following data is real. The percent of declared ethnic minority students at De Anza College for selected years from 1970–1995 was:

The independent variable is “Year,” while the independent variable is “Student Ethnic Minority Percent.”
Year Student Ethnic Minority Percentage
1970 14.13
1973 12.27
1976 14.08
1979 18.16
1982 27.64
1983 28.72
1986 31.86
1989 33.14
1992 45.37
1995 53.1
Student Ethnic Minority Percentage
By hand, verify the scatterplot above.

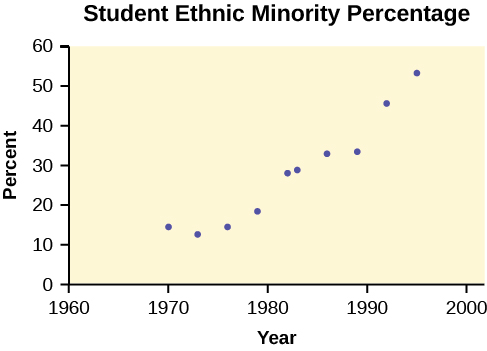
This is a scatterplot for the data provided. Year is plotted on the horizontal axis and percent is plotted on the vertical axis. The points show a strong, curved, upward trend.

Note

The TI-83 has a built-in linear regression feature, which allows the data to be edited.The x-values will be in [L1]; the y-values in [L2].

To enter data and do linear regression:

  1. ON Turns calculator on.
     on key

  2. Before accessing this program, be sure to turn off all plots.

    • Access graphing mode.
       2nd key , [STAT PLOT]

    • Turn off all plots.
       number 4 key , enter key

  3. Round to three decimal places. To do so:

    • Access the mode menu.
       mode key , [STAT PLOT]

    • Navigate to <Float> and then to the right to <3>.
       arrow down key arrow right key

    • All numbers will be rounded to three decimal places until changed.
       enter key

  4. Enter statistics mode and clear lists [L1] and [L2], as describe previously.
     stat key , number 4 key

  5. Enter editing mode to insert values for x and y.
     stat key , enter key

  6. Enter each value. Press enter key to continue.

To display the correlation coefficient:

  1. Access the catalog.
     2nd key , [CATALOG]

  2. Arrow down and select <DiagnosticOn>
     arrow down key… , enter key , enter key

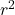  3. r and {r}^{2} will be displayed during regression calculations.

  4. Access linear regression.
     stat key arrow right key

  5. Select the form of y = a + bx.
     number 8 key , enter key


The display will show:

LinReg

  • y = a + bx
  • a = –3176.909
  • b = 1.617
  • r = 2 0.924
  • r = 0.961


This means the Line of Best Fit (Least Squares Line) is:

  • y = –3176.909 + 1.617x
  • Percent = –3176.909 + 1.617 (year #)

The correlation coefficient r = 0.961

To see the scatter plot:

  1. Access graphing mode.
     2nd key , [STAT PLOT]

  2. Select <1:plot 1> To access plotting – first graph.
     enter key

  3. Navigate and select <ON> to turn on Plot 1.
     <ON> enter key

  4. Navigate to the first picture.

  5. Select the scatter plot.
     enter key

  6. Navigate to <Xlist>.
  7. If [L1] is not selected, press 2nd key , [L1] to select it.

  8. Confirm that the data values are in [L1].
     <ON> enter key

  9. Navigate to <Ylist>.

  10. Select that the frequencies are in [L2].
     2nd key , [L2] , enter key

  11. Go back to access other graphs.
     2nd key , [STAT PLOT]

  12. Use the arrows to turn off the remaining plots.
  13. Access window mode to set the graph parameters.
     window key

    • {X}_{\mathrm{min}}=1970
    • {X}_{\mathrm{max}}=2000
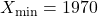
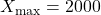
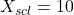    • {X}_{scl}=10 (spacing of tick marks on x-axis)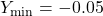
    • {Y}_{\mathrm{min}}=-0.05
    • {Y}_{\mathrm{max}}=60
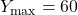
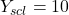    • {Y}_{scl}=10 (spacing of tick marks on y-axis)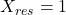
    • {X}_{res}=1
  14. Be sure to deselect or clear all equations before graphing, using the instructions above.
  15. Press the graph button to see the scatter plot. graph key

To see the regression graph:

  1. Access the equation menu. The regression equation will be put into Y1.
     Y= key

  2. Access the vars menu and navigate to <5: Statistics>.
     vars key , number 5 key

  3. Navigate to <EQ>.

  4. <1: RegEQ> contains the regression equation which will be entered in Y1.
     enter key

  5. Press the graphing mode button. The regression line will be superimposed over the scatter plot.
     graph key

To see the residuals and use them to calculate the critical point for an outlier:

  1. Access the list. RESID will be an item on the menu. Navigate to it.
     2nd key, [LIST], <RESID>

  2. Confirm twice to view the list of residuals. Use the arrows to select them.
     enter key , enter key

  3. The critical point for an outlier is: 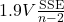1.9V\frac{\mathrm{SSE}}{n-2} where:
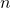    • n = number of pairs of data
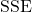    • \mathrm{SSE} = sum of the squared errors
    • \sum _{}^{}{\mathrm{residual}}^{2}

  4. Store the residuals in [L3].
     store key , 2nd key , [L3] , enter key

  5. Calculate the 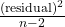\frac{{\mathrm{\left(residual\right)}}^{2}}{n-2}. Note that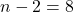 n-2=8
    2nd key , [L3] , x-squared key , division key , number 8 key

  6. Store this value in [L4].
     store key , 2nd key , [L4] , enter key

  7. Calculate the critical value using the equation above.
     number 1 key , decimal point key , number 9 key , multiplication key , 2nd key , [V] , 2nd key , [LIST] arrow right key , arrow right key , number 5 key , 2nd key , [L4] , closing parenthesis key , closing parenthesis key , enter key

  8. Verify that the calculator displays: 7.642669563. This is the critical value.
  9. Compare the absolute value of each residual value in [L3] to 7.64. If the absolute value is greater than 7.64, then the (x, y) corresponding point is an outlier. In this case, none of the points is an outlier.

To obtain estimates of y for various x-values:There are various ways to determine estimates for “y.” One way is to substitute values for “x” in the equation. Another way is to use the trace key on the graph of the regression line.

TI-83, 83+, 84, 84+ instructions for distributions and tests

Distributions

Access DISTR (for “Distributions”).

For technical assistance, visit the Texas Instruments website at http://www.ti.com and enter your calculator model into the “search” box.

Binomial Distribution

  • binompdf(n,p,x) corresponds to P(X = x)
  • binomcdf(n,p,x) corresponds to P(X ≤ x)
  • To see a list of all probabilities for x: 0, 1, . . . , n, leave off the “x” parameter.

Poisson Distribution

  • poissonpdf(λ,x) corresponds to P(X = x)
  • poissoncdf(λ,x) corresponds to P(X ≤ x)

Continuous Distributions (general)

  • -\infty uses the value –1EE99 for left bound
  • \infty uses the value 1EE99 for right bound

Normal Distribution

  • normalpdf(x,μ,σ) yields a probability density function value (only useful to plot the normal curve, in which case “x” is the variable)
  • normalcdf(left bound, right bound, μ, σ) corresponds to P(left bound < X < right bound)
  • normalcdf(left bound, right bound) corresponds to P(left bound < Z < right bound) – standard normal
  • invNorm(p,μ,σ) yields the critical value, k: P(X < k) = p
  • invNorm(p) yields the critical value, k: P(Z < k) = p for the standard normal

Student’s t-Distribution

  • tpdf(x,df) yields the probability density function value (only useful to plot the student-t curve, in which case “x” is the variable)
  • tcdf(left bound, right bound, df) corresponds to P(left bound < t < right bound)

Chi-square Distribution

  • Χ2pdf(x,df) yields the probability density function value (only useful to plot the chi2 curve, in which case “x” is the variable)
  • Χ2cdf(left bound, right bound, df) corresponds to P(left bound < Χ2 < right bound)

F Distribution

  • Fpdf(x,dfnum,dfdenom) yields the probability density function value (only useful to plot the F curve, in which case “x” is the variable)
  • Fcdf(left bound,right bound,dfnum,dfdenom) corresponds to P(left bound < F < right bound)

Tests and Confidence Intervals

Access STAT and TESTS.

For the confidence intervals and hypothesis tests, you may enter the data into the appropriate lists and press DATA to have the calculator find the sample means and standard deviations. Or, you may enter the sample means and sample standard deviations directly by pressing STAT once in the appropriate tests.

Confidence Intervals

  • ZInterval is the confidence interval for mean when σ is known.
  • TInterval is the confidence interval for mean when σ is unknown; s estimates σ.
  • 1-PropZInt is the confidence interval for proportion.
Note

The confidence levels should be given as percents (ex. enter “95” or “.95” for a 95% confidence level).

Hypothesis Tests

  • Z-Test is the hypothesis test for single mean when σ is known.
  • T-Test is the hypothesis test for single mean when σ is unknown; s estimates σ.
  • 2-SampZTest is the hypothesis test for two independent means when both σ’s are known.
  • 2-SampTTest is the hypothesis test for two independent means when both σ’s are unknown.
  • 1-PropZTest is the hypothesis test for single proportion.
  • 2-PropZTest is the hypothesis test for two proportions.
  • Χ2-Test is the hypothesis test for independence.
  • Χ2GOF-Test is the hypothesis test for goodness-of-fit (TI-84+ only).
  • LinRegTTEST is the hypothesis test for Linear Regression (TI-84+ only).
Note

Input the null hypothesis value in the row below “Inpt.” For a test of a single mean, “μ∅” represents the null hypothesis. For a test of a single proportion, “p∅” represents the null hypothesis. Enter the alternate hypothesis on the bottom row.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

College Statistics Copyright © 2022 by St. Clair College is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book