4.3. Weighted Decision Matrix
A weighted decision matrix is a decision tool used by decision-makers.
A decision matrix is basically an array presenting on one axis a list of alternatives, also called options or solutions. On the other axis, is a list of criteria, which are weighted depending on their respective importance in the final decision to be taken.
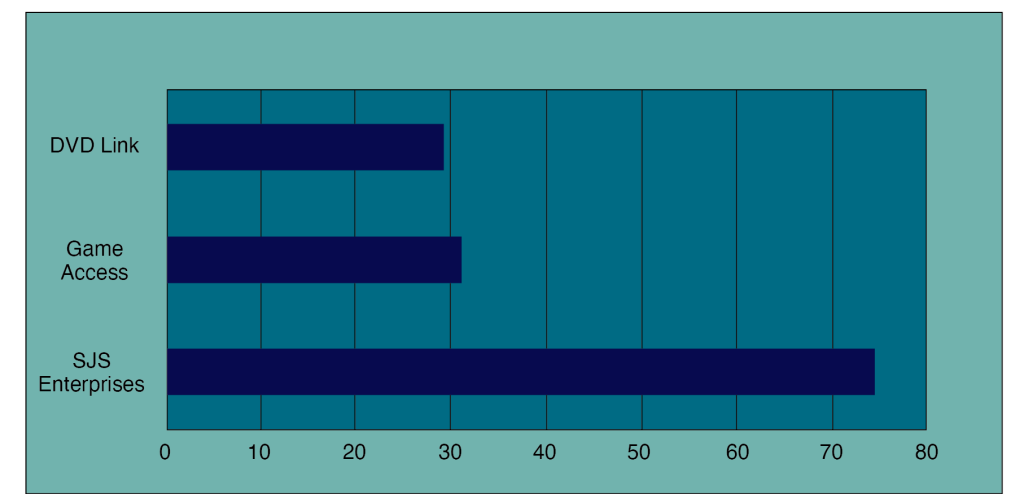
The example in Figure 4.2 shows a weighted decision matrix that compared three options for a web development project (SJS Enterprises). This method is especially useful when choosing purchase alternatives and comparing them against specific desirable system requirements.
Table 4.1 Weighted Decision Matrix for Game Delivery System
| Criteria | Weight | SJS Enterprises | Game Access | DVD Link |
|---|---|---|---|---|
| Educational | 15% | 90 | 0 | 0 |
| Sports-related | 15% | 90 | 90 | 90 |
| Secure payment area with the ability to use Paypal, bank payments, cheques, school payment systems as a payment source | 10% | 90 | 50 | 50 |
| Live Support | 15% | 90 | 0 | 0 |
| Search Option | 5% | 50 | 50 | 30 |
| Games available for all platforms currently on the market including school learning systems | 10% | 60 | 30 | 30 |
| Longer Rental Periods (1 to 2 weeks) | 5% | 40 | 20 | 40 |
| Sidebar with categories such as most popular, multiplayer, and just released | 5% | 50 | 50 | 20 |
| Registered customers must be able to order the videos, track delivery, return of videos and be able to provide reviews of views | 10% | 50 | 30 | 30 |
| Age/grade appropriate section (can isolate certain games to certain ages or grade levels) | 10% | 70 | 5 | 0 |
| Weighted Project Scores | 100% | 74.5 | 31 | 29 |
Comparing Options Using a Weighted Decision Matrix
Sometimes we have multiple options to choose from when determining requirements and deciding which project to work on. To select the best option, we can use tools such as a weighted decision matrix.
A basic decision matrix consists of establishing a set of criteria for options that are scored and summed to gain a total score that can then be ranked. Importantly, it is not weighted to allow a quick selection process.
A weighted decision matrix operates in the same way as the basic decision matrix but introduces the concept of weighting the criteria in order of importance. The resultant scores better reflect the importance to the decision maker of the criteria involved. The more important a criterion, the higher the weighting it should be given. Each of the potential options is scored and then multiplied by the weighting given to each of the criteria to produce a result.
The advantage of the weighted decision matrix is that subjective opinions about one alternative versus another can be made more objective. Another advantage of this method is that sensitivity studies can be performed. An example of this might be to see how much your opinion would have to change in order for a lower-ranked alternative to outrank a competing alternative.
A weighted decision matrix therefore allows decision-makers to structure and solve their problems by:
- Specifying and prioritizing their needs with a list of criteria; then
- Evaluating, rating, and comparing the different solutions; and
- Selecting the best matching solution.
“7. Project Initiation” from Project Management – 2nd Edition by Adrienne Watt; Merrie Barron; and Andrew Barron is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

