Mathematical Phrases, Symbols, and Formulas

Adapted by John Morgan Russell; from Barbara Illowsky and Susan Dean, David Diez, Mine Cetinkaya-Rundel and Christopher D. Barr; Julie Vu and David Harrington

Mathematical Phrases, Symbols, and Formulas

English Phrases Written Mathematically

When the English says:	Interpret this as:
X is at least 4.	X ≥ 4
The minimum of X is 4.	X ≥ 4
X is no less than 4.	X ≥ 4
X is greater than or equal to 4.	X ≥ 4
X is at most 4.	X ≤ 4
The maximum of X is 4.	X ≤ 4
X is no more than 4.	X ≤ 4
X is less than or equal to 4.	X ≤ 4
X does not exceed 4.	X ≤ 4
X is greater than 4.	X > 4
X is more than 4.	X > 4
X exceeds 4.	X > 4
X is less than 4.	X < 4
There are fewer X than 4.	X < 4
X is 4.	X = 4
X is equal to 4.	X = 4
X is the same as 4.	X = 4
X is not 4.	X ≠ 4
X is not equal to 4.	X ≠ 4
X is not the same as 4.	X ≠ 4
X is different than 4.	X ≠ 4

Formulas

Formula 1: Factorial

$n!=n\left(n-1\right)\left(n-2\right)...\left(1\right)\text{}$

$0!=1\text{}$

Formula 2: Combinations

$\left(\begin{array}{l}n\\ r\end{array}\right)=\frac{n!}{\left(n-r\right)!r!}$

Formula 3: Binomial Distribution

$X\phantom{\rule{2px}{0ex}}~\phantom{\rule{2px}{0ex}}B\left(n,p\right)$

$P\left(X=x\right)=\left(\begin{array}{c}n\\ x\end{array}\right){p}^{x}{q}^{n-x}$ , for $x=0,1,2,...,n$

Formula 4: Geometric Distribution

$X\phantom{\rule{2px}{0ex}}~\phantom{\rule{2px}{0ex}}G\left(p\right)$

$P\left(X=x\right)={q}^{x-1}p$ , for $x=1,2,3,...$

Formula 5: Hypergeometric Distribution

$X\phantom{\rule{2px}{0ex}}~\phantom{\rule{2px}{0ex}}H\left(r,b,n\right)$

$P\text{(}X=x\text{)}=\left(\frac{\left(\genfrac{}{}{0}{}{r}{x}\right)\left(\genfrac{}{}{0}{}{b}{n-x}\right)}{\left(\genfrac{}{}{0}{}{r+b}{n}\right)}\right)$

Formula 6: Poisson Distribution

$X\phantom{\rule{2px}{0ex}}~\phantom{\rule{2px}{0ex}}P\left(\mu \right)$

$P\text{(}X=x\text{)}=\frac{{\mu }^{x}{e}^{-\mu }}{x!}$

Formula 7: Uniform Distribution

$X\phantom{\rule{2px}{0ex}}~\phantom{\rule{2px}{0ex}}U\left(a,b\right)$

$f\left(X\right)=\frac{1}{b-a}$ , $a<x<b$

Formula 8: Exponential Distribution

$X\phantom{\rule{2px}{0ex}}~\phantom{\rule{2px}{0ex}}Exp\left(m\right)$

$f\left(x\right)=m{e}^{-mx}m>0,x\ge 0$

Formula 9: Normal Distribution $X\phantom{\rule{2px}{0ex}}~\phantom{\rule{2px}{0ex}}N\left(\mu ,{\sigma }^{2}\right)$

$f\text{(}x\text{)}=\frac{1}{\sigma \sqrt{2\pi }}{e}^{\frac{{-\left(x-\mu \right)}^{2}}{{2\sigma }^{2}}}$ , $\phantom{\rule{12pt}{0ex}}-\infty <x<\infty$

Formula 10: Gamma Function

$\Gamma \left(z\right)=\underset{\infty }{\overset{0}{{\int }^{\text{}}}}{x}^{z-1}{e}^{-x}dx$ $z>0$

$\Gamma \left(\frac{1}{2}\right)=\sqrt{\pi }$

$\Gamma \left(m+1\right)=m!$ for $m$ , a nonnegative integer

otherwise: $\Gamma \left(a+1\right)=a\Gamma \left(a\right)$

Formula 11: Student’s t-distribution

$X\phantom{\rule{2px}{0ex}}~\phantom{\rule{2px}{0ex}}{t}_{df}$

$f\text{(}x\text{)}=\frac{{\left(1+\frac{{x}^{2}}{n}\right)}^{\frac{-\left(n+1\right)}{2}}\Gamma \left(\frac{n+1}{2}\right)}{\sqrt{\mathrm{n\pi }}\Gamma \left(\frac{n}{2}\right)}$

$X=\frac{Z}{\sqrt{\frac{Y}{n}}}$

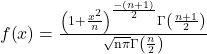
$Z\phantom{\rule{2px}{0ex}}~\phantom{\rule{2px}{0ex}}N\left(0,1\right),\phantom{\rule{2px}{0ex}}Y\phantom{\rule{2px}{0ex}}~\phantom{\rule{2px}{0ex}}{Χ}_{df}^{2}$ , $n$ = degrees of freedom

Formula 12: Chi-Square Distribution

$X\phantom{\rule{2px}{0ex}}~\phantom{\rule{2px}{0ex}}{Χ}_{df}^{2}$

$f\text{(}x\text{)}=\frac{{x}^{\frac{n-2}{2}}{e}^{\frac{-x}{2}}}{{2}^{\frac{n}{2}}\Gamma \left(\frac{n}{2}\right)}$ , $x>0$ , $n$ = positive integer and degrees of freedom

Formula 13: F Distribution

$X\phantom{\rule{2px}{0ex}}~\phantom{\rule{2px}{0ex}}{F}_{df\left(n\right),df\left(d\right)}$

$df\left(n\right)\phantom{\rule{2px}{0ex}}=\phantom{\rule{2px}{0ex}}$ degrees of freedom for the numerator

$df\left(d\right)\phantom{\rule{2px}{0ex}}=\phantom{\rule{2px}{0ex}}$ degrees of freedom for the denominator

$f\left(x\right)=\frac{\Gamma \left(\frac{u+v}{2}\right)}{\Gamma \left(\frac{u}{2}\right)\Gamma \left(\frac{v}{2}\right)}{\left(\frac{u}{v}\right)}^{\frac{u}{2}}{x}^{\left(\frac{u}{2}-1\right)}\left[1+\left(\frac{u}{v}\right){x}^{-0.5\left(u+v\right)}\right]$

$X=\frac{{Y}_{u}}{{W}_{v}}$ , $Y$ , $W$ are chi-square

Symbols and Their Meanings

Symbols and their Meanings
Chapter (1st used)	Symbol	Spoken	Meaning
Sampling and Data	$\sqrt{\begin{array}{c}\text{ }\\ \text{ }\end{array}}$	The square root of	same
Sampling and Data	$\pi$	Pi	3.14159… (a specific number)
Descriptive Statistics	Q₁	Quartile one	the first quartile
Descriptive Statistics	Q₂	Quartile two	the second quartile
Descriptive Statistics	Q₃	Quartile three	the third quartile
Descriptive Statistics	IQR	interquartile range	Q₃ – Q₁ = IQR
Descriptive Statistics	$\overline{x}$	x-bar	sample mean
Descriptive Statistics	$\mu$	mu	population mean
Descriptive Statistics	ss_xsx	s	sample standard deviation
Descriptive Statistics	${s}^{2}$ ${s}_{x}^{2}$	s squared	sample variance
Descriptive Statistics	$\sigma$ ${\sigma }_{x}$ σx	sigma	population standard deviation
Descriptive Statistics	${\sigma }^{2}$ ${\sigma }_{x}^{2}$	sigma squared	population variance
Descriptive Statistics	$\Sigma$	capital sigma	sum
Probability Topics	$\left\{\right\}$	brackets	set notation
Probability Topics	$S$	S	sample space
Probability Topics	$A$	Event A	event A
Probability Topics	$P\left(A\right)$	probability of A	probability of A occurring
Probability Topics	$P\left(\mathit{\text{A}}\text{\|}\mathit{\text{B}}\right)$	probability of A given B	prob. of A occurring given B has occurred
Probability Topics	$P\left(A\text{ OR }B\right)$	prob. of A or B	prob. of A or B or both occurring
Probability Topics	$P\left(A\text{ AND }B\right)$	prob. of A and B	prob. of both A and B occurring (same time)
Probability Topics	A′	A-prime, complement of A	complement of A, not A
Probability Topics	P(A‘)	prob. of complement of A	same
Probability Topics	G₁	green on first pick	same
Probability Topics	P(G₁)	prob. of green on first pick	same
Discrete Random Variables	PDF	prob. distribution function	same
Discrete Random Variables	X	X	the random variable X
Discrete Random Variables	X ~	the distribution of X	same
Discrete Random Variables	B	binomial distribution	same
Discrete Random Variables	G	geometric distribution	same
Discrete Random Variables	H	hypergeometric dist.	same
Discrete Random Variables	P	Poisson dist.	same
Discrete Random Variables	$\lambda$	Lambda	average of Poisson distribution
Discrete Random Variables	$\ge$	greater than or equal to	same
Discrete Random Variables	$\le$	less than or equal to	same
Discrete Random Variables	=	equal to	same
Discrete Random Variables	≠	not equal to	same
Continuous Random Variables	f(x)	f of x	function of x
Continuous Random Variables	pdf	prob. density function	same
Continuous Random Variables	U	uniform distribution	same
Continuous Random Variables	Exp	exponential distribution	same
Continuous Random Variables	k	k	critical value
Continuous Random Variables	f(x) =	f of x equals	same
Continuous Random Variables	m	m	decay rate (for exp. dist.)
The Normal Distribution	N	normal distribution	same
The Normal Distribution	z	z-score	same
The Normal Distribution	Z	standard normal dist.	same
The Central Limit Theorem	CLT	Central Limit Theorem	same
The Central Limit Theorem	$\overline{X}$	X-bar	the random variable X-bar
The Central Limit Theorem	${\mu }_{x}$	mean of X	the average of X
The Central Limit Theorem	${\mu }_{\overline{x}}$	mean of X-bar	the average of X-bar
The Central Limit Theorem	${\sigma }_{x}$	standard deviation of X	same
The Central Limit Theorem	${\sigma }_{\overline{x}}$	standard deviation of X-bar	same
The Central Limit Theorem	$\Sigma X$	sum of X	same
The Central Limit Theorem	$\Sigma x$	sum of x	same
Confidence Intervals	CL	confidence level	same
Confidence Intervals	CI	confidence interval	same
Confidence Intervals	EBM	error bound for a mean	same
Confidence Intervals	EBP	error bound for a proportion	same
Confidence Intervals	t	Student’s t-distribution	same
Confidence Intervals	df	degrees of freedom	same
Confidence Intervals	${t}_{\frac{\alpha }{2}}$	student t with a/2 area in right tail	same
Confidence Intervals	$p\prime$ ; $\stackrel{^}{p}$	p-prime; p-hat	sample proportion of success
Confidence Intervals	$q\prime$ ; $\stackrel{^}{q}$	q-prime; q-hat	sample proportion of failure
Hypothesis Testing	${H}_{0}$	H-naught, H-sub 0	null hypothesis
Hypothesis Testing	${H}_{a}$	H-a, H-sub a	alternate hypothesis
Hypothesis Testing	${H}_{1}$	H-1, H-sub 1	alternate hypothesis
Hypothesis Testing	$\alpha$	alpha	probability of Type I error
Hypothesis Testing	$\beta$	beta	probability of Type II error
Hypothesis Testing	$\overline{X1}-\overline{X2}$	X1-bar minus X2-bar	difference in sample means
Hypothesis Testing	${\mu }_{1}-{\mu }_{2}$	mu-1 minus mu-2	difference in population means
Hypothesis Testing	${{P}^{\prime }}_{1}-{{P}^{\prime }}_{2}$	P1-prime minus P2-prime	difference in sample proportions
Hypothesis Testing	${p}_{1}-{p}_{2}$	p1 minus p2	difference in population proportions
Chi-Square Distribution	${Χ}^{2}$	Ky-square	Chi-square
Chi-Square Distribution	$O$	Observed	Observed frequency
Chi-Square Distribution	$E$	Expected	Expected frequency
Linear Regression and Correlation	y = a + bx	y equals a plus b-x	equation of a line
Linear Regression and Correlation	$\stackrel{^}{y}$	y-hat	estimated value of y
Linear Regression and Correlation	$r$	correlation coefficient	same
Linear Regression and Correlation	$\epsilon$	error	same
Linear Regression and Correlation	SSE	Sum of Squared Errors	same
Linear Regression and Correlation	1.9s	1.9 times s	cut-off value for outliers
F-Distribution and ANOVA	F	F-ratio	F-ratio