Queer
David Szanto
David Szanto is a teacher, consultant, and artist taking an experimental approach to gastronomy and food systems. Past projects include meal performances about urban foodscapes, immersive sensory installations, and interventions involving food, microbes, humans, and digital technology. David has taught at several universities in Canada and Europe and has written extensively on food, art, and performance.
Twisting ‘Truth’
Take a letter-sized piece of paper and cut it into three roughly equal pieces, each about 2.8” x 11” (7.2cm x 18cm). Tape the short end of one piece to that of another piece, then tape on the third piece in the same way. Take the end of the third piece, give it a half twist, and then tape it to the start of the first piece. You now have what is called a Moebius strip, a loop in which that half-twist allows the ‘inside’ of the paper to be continuous with the ‘outside’. If you run a pencil along one side of the paper, you will eventually draw a continuous line that appears on ‘both sides’ of the strip. While this seems like an obvious effect of a twisted piece of paper, the Moebius strip is a useful way of understanding ‘truths’ in variable ways. The first of these truths is that the inside of something can be the same as its outside.

Now take a pair of scissors, pierce the strip along the pencil line, and then keep cutting until you have divided the strip in two. But wait, it’s not “in two,” is it? Now you have a large loop of paper with two twists in it. You cut a whole thing into two pieces, but somehow it’s still just one piece. Where did the cut go?

You’re not done yet! Pierce the strip again with the scissors, and cut down the length of it as you did the first time. (You don’t need to draw the pencil line, but you can if you want, to sense the new loop’s double twist.) Once you’ve cut the large loop down its center, what do you have? (You might want to ask a friend at this point to help you hold it up.) The new result is two loops that intersect each other, like two links in a chain. (The two loops also have their own twists, which can make it a little difficult to see that they are in fact separate.)

What’s going on here?
The mathematics of a Moebius strip are relatively straightforward, yet its properties are provocative, both in math and in more humanistic thinking. Conceptually, the strip exists in multiple states at once, and its behaviours (for example, when we draw on it or cut it up) don’t seem to follow our expectations for ‘normal’ pieces of paper. Its inside is its outside, meaning it seems to have two sides, but it actually only has one. Divided, it remains whole, but when we cut it again, it links itself together. Is it a loop? Is it a single surface? Is it two loops disguised as one, or one loop disguised as two?
Again, mathematicians (or Wikipedia) can answer these questions pretty clearly, but when you leave some space in your mind to ponder them more philosophically, they help understand the concept of queer. This includes the ways that queer theory can help us think about the world without necessarily relying on knowledge frameworks founded on ordering and categorization, or on ‘truths’ that are assumed to be universal.
What if we had a radically different way of understanding the world around us, including the ‘laws’ of science and the ‘reality’ of humanity? What if we could step out of our normative frameworks of seeing and interpreting things, and somehow perceive gravity, identity, math, beauty, language, or society in ways that were not dependent on the definitions of other people and the knowledge of experts? What if we could twist the world, just a bit, in order to think and feel and act in ways that we never have before?
These are some of the questions that queer theorists address. They are important questions in terms of moving ourselves forward as a species, while building greater justice and diversity into the ways in which we treat each other, understand reality, and find innovative solutions to complex problems. In some ways, thinking and doing things through queer-ness is about being provocative in order to provoke change.
The etymological genealogy of “queer” is also provocative. There seem to be a number of possible origins of the word, including Scottish and German roots from as early as the year 1500, though some of these are contested. Terms such as oblique, twisted, off-center, and odd point to a history in which ‘non-square’ and ‘unusual’ were close to synonymous. This suggests normalcy and linearity were closely associated long before the advent of the technologies that have enabled humans to design precise edges and crisp shapes. As we have refined our abilities to engineer and measure and define things, normativity and straight-ness have also converged in meaning.
Today, one of our common uses of “queer” is to describe people who identify in ways that differ from normative heterosexuality. It thus becomes an umbrella term that says both ‘not straight’ and ‘open to alternative interpretations’. While some LGBTQIA2+ people do not identify as “queer,” many find it to be a useful way to encompass a range of diverse perspectives on humanness, including sex, sexuality, gender, body shape, ability, and world view.
Yet queer is also useful as a way to twist our basic assumptions, from a theoretical perspective, about what we understand to be true. A queer perspective on family, for example, interprets close human collectives in ways that move beyond a parental binary with offspring who are raised (fed, clothed, loved, educated, socialized) by those parents. This might include young people who care for their elders, multiple caregivers for a single individual, groups that are not genetically related, or more fluid combinations of people who come and go from a household (or who never are part of a household to begin with).
How can queer help us think differently about other social, environmental, artistic, economic, scientific, governance, philosophical, and gastronomic ‘realities’? If the ordinary, normal, and standard ways that we perceive the world were to be twisted and re-understood according to a loopy, two-sided, and entangled ‘logic’, what might we end up seeing? How might we end up doing, feeling, and being differently, both individually and collectively?
Discussion Questions
- In what ways are you queer? In what ways are you normative?
- In their book, The Queer Art of Failure, Judith (Jack) Halberstam reinterprets failure as a positive, alternate outcome of a situation, one that is not the opposite of success, nor a necessary step in reaching success. Instead, forgetting, being ‘stupid’ or accident prone, and not winning are all understood as good, useful, and creatively productive.
- In your own life, imagine a time when you ‘failed’. Is there a way to understand that failure as satisfying, joyful, or valuable? Can you do so without saying to yourself, “Well, at least that failure brought me closer to success…”?
- Is this an easy challenge or a hard one? Why? What allows or prevents you from imagining failure as good? In your own experience, what shapes the way you understand failure and success?
- Watch the video “Failing” and discuss what is depicted. Is this a queer representation of failure? of success? of something else?
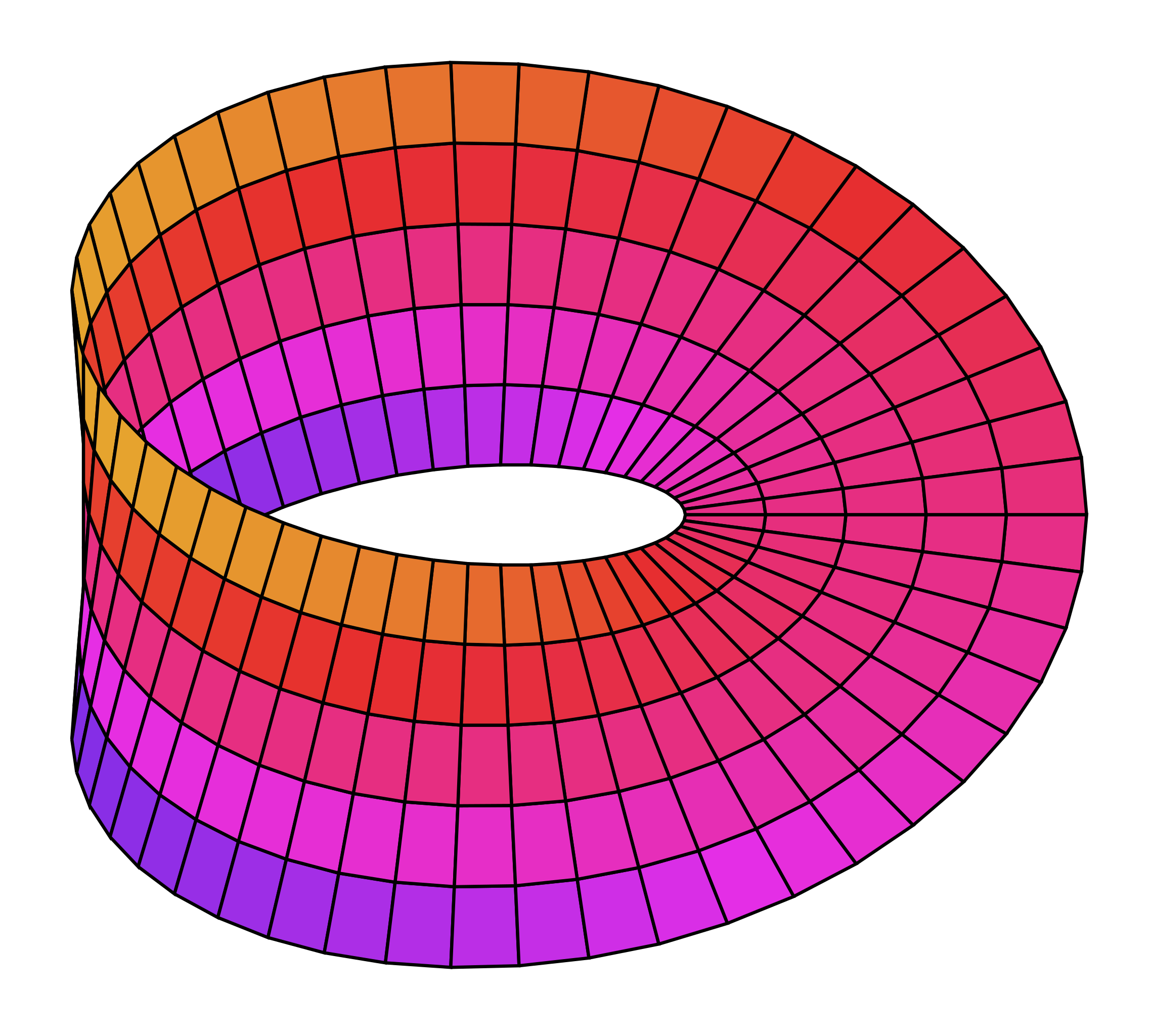
- The image below of a Moebius strip helps make the topography of the surface(s) more apparent, as do the gradations in colour of the small trapezoidal segments that compose it. How does this ‘clarity’ help and/or hinder your understanding of the analogy made about queerness?
Additional Resources
Butler, J. (1993). Bodies That Matter: On the Discursive Limits of “Sex”. Routledge.
Halberstam, J. (2011). The Queer Art of Failure. Duke University Press.
Maroney, S. (2018). Sandor Katz and the Possibilities of a Queer Fermentive Praxis. Cuizine : The Journal of Canadian Food CulturesCuizine : / Revue Des Cultures Culinaires Au Canada, 9(2). https://doi.org/10.7202/1055217ar
Moon, M., & Sedgwick, E. K. (1994). Queers in (Single-Family) Space. Assemblage, 24, 30–37. https://doi.org/10.2307/3171189
Schutzer, C. (2011, June 7). Failing—A very difficult piece for solo string bass. https://www.youtube.com/watch?v=9P8C6-XqaNs
Seidman, S. (1994). Queer-Ing Sociology, Sociologizing Queer Theory: An Introduction. Sociological Theory, 12(2), 166. https://doi.org/10.2307/201862
Not so much a single idea or set of theorizations, queer theory is a perspective on the world that aims to evade the normativities of “given knowledge,” such as social or scientific ‘truth.’ Instead, queer theory supports alternative ways of perceiving what is normal. It also suggests that there is value in radically shifting the frameworks, assumptions, and foundations that support our understanding of reality. Often this means taking cues from queer human experience—such as those of sex, sexuality, identity, social dynamics, and personal expression—and applying those cues to broader contexts.
Something that is normative follows those standards that are commonly set, adhered to, and reinforced by a dominant or majority group. This may include the standards (or “norms”) of a society, a natural environment, or a scientific method or practice. Although the two words are often conflated, normative does not mean normal (itself a complex concept).
Of pertaining to the origin of a word or words. Important to this term is the meaning of words and how they shift, historically.
Etymologically, to “define” something is to express its meaning in a way that puts an end to the discussion about that meaning. Definitions thus allow for many people to share a single, common understanding of a term or concept. Definitions are therefore considered authoritative, for better and for worse. Importantly, definitions are created by individuals or institutions that necessarily bring their own motivations and knowledge frameworks, and therefore imbue definitions with power and bias.

