2.5 Solve Applications with Rational Equations
Learning Objectives
By the end of this section, you will be able to:
- Solve proportions
- Solve similar figure applications
- Solve uniform motion applications
- Solve work applications
- Solve direct variation problems
- Solve inverse variation problems
Try It
Before you get started, take this readiness quiz:
1) Solve: [latex]2(n-1)-4=-10[/latex].
2) An express train and a charter bus leave Chicago to travel to Champaign. The express train can make the trip in two hours and the bus takes five hours for the trip. The speed of the express train is [latex]42[/latex] miles per hour faster than the speed of the bus. Find the speed of the bus.
3) Solve [latex]\frac{1}{3}x+\frac{1}{4}x=\frac{5}{6}[/latex].
Solve Proportions
When two rational expressions are equal, the equation relating them is called a proportion.
Proportion
A proportion is an equation of the form [latex]\frac{a}{b}=\frac{c}{d}[/latex], where [latex]b\neq0,d\neq0[/latex].
The proportion is read “[latex]a[/latex] is to [latex]b[/latex] as [latex]c[/latex] is to [latex]d[/latex].”
The equation [latex]\frac{1}{2}=\frac{4}{8}[/latex] is a proportion because the two fractions are equal. The proportion [latex]\frac{1}{2}=\frac{4}{8}[/latex] is read “[latex]1[/latex] is to [latex]2[/latex] as [latex]4[/latex] is to [latex]8[/latex].”
Since a proportion is an equation with rational expressions, we will solve proportions the same way we solved rational equations. We’ll multiply both sides of the equation by the LCD to clear the fractions and then solve the resulting equation.
Example 2.5.1
Solve: [latex]\frac{n}{n+14}=\frac{5}{7}[/latex].
Solution
Step 1: Multiply both sides by LCD.
[latex]{\color{Red}{7(n+14)}}\left(\frac{n}{n+14}\right)={\color{Red}{7(n+14)}}\left(\frac57\right)[/latex]
Step 2: Remove common factors on each side.
[latex]7n=5(n+14)[/latex]
Step 3: Simplify.
[latex]7n=5n+70[/latex]
Step 4: Solve for [latex]n[/latex].
[latex]\begin{align*}2n&=70\\n&=35\end{align*}[/latex]
Step 5: Check.
[latex]\begin{align*} &\;&\frac{n}{n+14}&=\frac57\\[2ex] &\text{Substitute}\;n={\color{Red}{35}}\;\;\;&\frac{{\color{Red}{35}}}{{\color{Red}{35}}+14}&\overset{?}{=}\frac57\\[2ex] &\text{Simplify.}\;\;\;&\frac{35}{49}&\overset{?}{=}\frac57\\[2ex] &\text{Show common factors.}\;\;\;&\frac{5\cdot7}{7\cdot7}&\overset{?}{=}\frac57\\[2ex] &\text{Simplify.}\;\;\;&\frac57&=\frac57\checkmark \end{align*}[/latex]
Try It
4) Solve the proportion: [latex]\frac{y}{y+55}=\frac{3}{8}[/latex].
Solution
[latex]y=33[/latex]
Try It
5) Solve the proportion: [latex]\frac{z}{z-84}=-\frac{1}{5}[/latex].
Solution
[latex]z=14[/latex]
Notice in the last example that when we cleared the fractions by multiplying by the LCD, the result is the same as if we had cross-multiplied.
[latex]\begin{array}{rcllrcl}\frac n{n+14}&=&\frac57&\;\;\;\;\;\;\;\;\;\;\;&\frac n{n+14}&=&\frac57\\{\color{red}{7}}{\color{red}{(}}{\color{red}{n}}{\color{red}{+}}{\color{red}{14}}{\color{red}{)}}\left(\frac n{n+14}\right)&=&{\color{red}{7}}{\color{red}{(}}{\color{red}{n}}{\color{red}{+}}{\color{red}{14}}{\color{red}{)}}\left(\frac57\right)&\;\;\;\;\;\;\;\;\;\;&\cancel{\bcancel{\frac n{n+14}}}&=&\bcancel{\cancel{\frac57}}\\7n&=&5(n+14)&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;&7n&=&5(n+14)\end{array}[/latex]
For any proportion, [latex]\frac{a}{b}=\frac{c}{d}[/latex], we get the same result when we clear the fractions by multiplying by the LCD as when we cross-multiply.
[latex]\begin{array}{ccc}\frac ab=\frac cd&\;\;\;\;\;\;\;\;\;\;&\frac ab=\frac cd\\{\color{red}{b}}{\color{red}{d}}\left(\frac ab=\frac cd\right){\color{red}{b}}{\color{red}{d}}&\;\;\;\;\;\;\;\;\;\;\;&\xcancel{\frac ab=\frac cd}\\ad=bc&\;\;\;\;\;\;\;\;\;\;&ad=bc\end{array}[/latex]
To solve applications with proportions, we will follow our usual strategy for solving applications But when we set up the proportion, we must make sure to have the units correct—the units in the numerators must match each other and the units in the denominators must also match each other.
Example 2.5.2
When pediatricians prescribe acetaminophen to children, they prescribe [latex]5[/latex] millilitres (ml) of acetaminophen for every [latex]25[/latex] pounds of the child’s weight. If Zoe weighs [latex]80[/latex] pounds, how many millilitres of acetaminophen will her doctor prescribe?
Solution
Step 1: Identify what we are asked to find, and choose a variable to represent it.
How many ml of acetaminophen will the doctor prescribe?
Let [latex]a=\text{ml of acetaminophen.}[/latex]
Step 2: Write a sentence that gives the information to find it.
If [latex]5[/latex] ml is prescribed for every [latex]25[/latex] pounds, how much will be prescribed for [latex]80[/latex] pounds?
Step 3: Translate into a proportion—be careful of the units.
[latex]\begin{align*}\frac{\mathrm{ml}}{\mathrm{pounds}}&=\frac{\mathrm{ml}}{\mathrm{pounds}}\\\frac5{25}&=\frac a{80}\end{align*}[/latex]
Step 4: Multiply both sides by the LCD, [latex]400[/latex].
[latex]{\color{Red}{400}}\left(\frac5{25}\right)={\color{Red}{400}}\left(\frac a{80}\right)[/latex]
Step 5: Remove common factors on each side.
[latex]{\color{Red}{\cancel{25}\cdot16}}\left(\frac5{\cancel{25}}\right)={\color{Red}{\cancel{80}\cdot5}}\left(\frac a{\cancel{80}}\right)[/latex]
Step 6: Simplify, but don’t multiply on the left. Notice what the next step will be.
[latex]16\cdot5=5a[/latex]
Step 7: Solve for [latex]a[/latex].
[latex]\begin{align*}\frac{16\cdot5}{\color{Red}{5}}&=\frac{5a}{\color{Red}{5}}\\16&=a\end{align*}[/latex]
Step 8: Check.
Is the answer reasonable?
Yes, since [latex]80[/latex] is about [latex]3[/latex] times [latex]25[/latex], the medicine should be about [latex]3[/latex] times [latex]5[/latex]. So [latex]16[/latex] ml makes sense. Substitute [latex]a={\color{Red}{16}}[/latex] in the original proportion.
[latex]\begin{align*}\frac5{25}&=\frac a{80}\\[2ex]\frac5{25}&\overset{?}{=} \frac{\color{Red}{16}}{80}\\[2ex]\frac15&=\frac15\checkmark\end{align*}[/latex]
Step 9: Write a complete sentence.
The pediatrician would prescribe [latex]16[/latex] ml of acetaminophen to Zoe.
Try It
6) Pediatricians prescribe [latex]5[/latex] millilitres (ml) of acetaminophen for every [latex]25[/latex] pounds of a child’s weight. How many millilitres of acetaminophen will the doctor prescribe for Emilia, who weighs [latex]60[/latex] pounds?
Solution
The pediatrician will prescribe [latex]12[/latex] ml of acetaminophen to Emilia.
Try It
7) For every [latex]1[/latex] kilogram (kg) of a child’s weight, pediatricians prescribe [latex]15[/latex] milligrams (mg) of a fever reducer. If Isabella weighs [latex]12[/latex] kg, how many milligrams of the fever reducer will the pediatrician prescribe?
Solution
The pediatrician will prescribe [latex]180[/latex] mg of fever reducer to Isabella.
Solve Similar Figure Applications
When you shrink or enlarge a photo on a phone or tablet, figure out a distance on a map, or use a pattern to build a bookcase or sew a dress, you are working with similar figures. If two figures have exactly the same shape, but different sizes, they are said to be similar. One is a scale model of the other. All their corresponding angles have the same measures and their corresponding sides have the same ratio.
Similar Figures
Two figures are similar if the measures of their corresponding angles are equal and their corresponding sides have the same ratio.
For example, the two triangles in Figure 2.5.1 are similar. Each side of [latex]\triangle ABC[/latex] is four times the length of the corresponding side of [latex]\triangle XYZ[/latex].
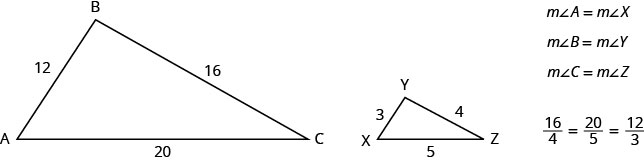
This is summed up in the Property of Similar Triangles.
Property of Similar Triangles
If [latex]\triangle ABC[/latex] is similar to [latex]\triangle XYZ[/latex], then their corresponding angle measure are equal and their corresponding sides have the same ratio.
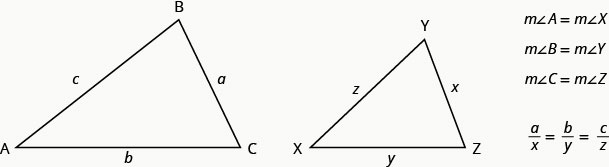
To solve applications with similar figures we will follow the Problem-Solving Strategy for Geometry Applications we used earlier.
Example 2.5.3
On a map, San Francisco, Las Vegas, and Los Angeles form a triangle. The distance between the cities is measured in inches. The figure on the left below represents the triangle formed by the cities on the map. If the actual distance from Los Angeles to Las Vegas is [latex]270[/latex] miles, find the distance from Los Angeles to San Francisco.
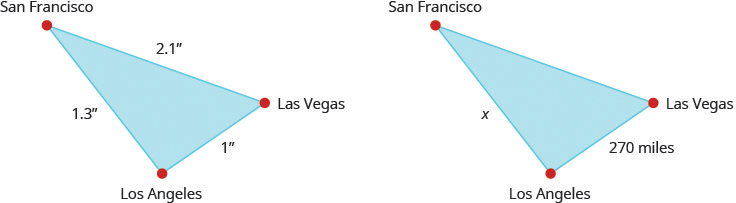
Solution
Step 1: Read the problem. Draw the figures and label it with the given information.
The figures are shown above.
Step 2: Identify what we are looking for.
The actual distance from Los Angeles to San Francisco
Step 3: Name the variables.
Let [latex]x=\text{distance}[/latex] from Los Angeles to San Francisco.
Step 4: Translate into an equation.
Since the triangles are similar, the corresponding sides are proportional. We’ll make the numerators “miles” and the denominators “inches”.
[latex]\frac{x\;\mathrm{miles}}{1.3\;\mathrm{inches}}=\frac{270\;\mathrm{miles}}{1\;\mathrm{inch}}[/latex]
Step 5: Solve the equation.
[latex]\begin{align*}{\color{Red}{1.3}}\left(\frac x{1.3}\right)&={\color{Red}{1.3}}\left(\frac{270}{1}\right)\\x&=351\end{align*}[/latex]
Step 6: Check.
On the map, the distance from Los Angeles to San Francisco is more than the distance from Los Angeles to Las Vegas. Since [latex]351[/latex] is more than [latex]270[/latex] the answer makes sense.
Check [latex]x={\color{Red}{351}}[/latex] in the original proportion.
Use a calculator.
[latex]\begin{align*}\frac{x\;\mathrm{miles}}{1.3\;\mathrm{inches}}&=\frac{270\;\mathrm{miles}}{1\;\mathrm{inch}}\\[2ex]\frac{{\color{Red}{351}}\;\mathrm{miles}}{1.3\;\mathrm{inches}} &\overset{?}{=} \frac{270\;\mathrm{miles}}{1\;\mathrm{inch}}\\[2ex]\frac{270\;\mathrm{miles}}{1\;\mathrm{inch}}&=\frac{270\;\mathrm{miles}}{1\;\mathrm{inch}}\checkmark\end{align*}[/latex]
Step 7: Answer the question.
The distance from Los Angeles to San Francisco is [latex]351[/latex] miles.
On the map, Seattle, Portland, and Boise form a triangle. The distance between the cities is measured in inches. The figure on the left below represents the triangle formed by the cities on the map. The actual distance from Seattle to Boise is [latex]400[/latex] miles.
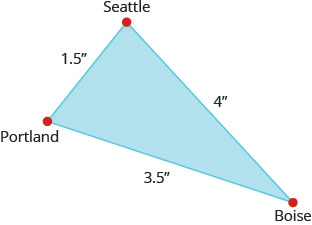
Try It
8) Find the actual distance from Seattle to Portland.
Solution
The distance is [latex]150[/latex] miles.
Try It
9) Find the actual distance from Portland to Boise.
Solution
The distance is [latex]350[/latex] miles.
We can use similar figures to find heights that we cannot directly measure.
Example 2.5.4
Tyler is [latex]6[/latex] feet tall. Late one afternoon, his shadow was [latex]8[/latex] feet long. At the same time, the shadow of a tree was [latex]24[/latex] feet long. Find the height of the tree.
Solution
Step 1: Read the problem and draw a figure.
We are looking for [latex]h[/latex], the height of the tree.
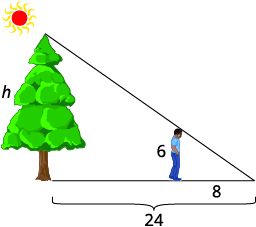
Step 2: We will use similar triangles to write an equation.
The small triangle is similar to the large triangle.
[latex]\frac h{24}=\frac68[/latex]
Step 3: Solve the proportion.
[latex]24\left(\frac68\right)=24\left(\frac h{24}\right)[/latex]
Step 4: Simplify.
[latex]18=h[/latex]
Step 5: Check.
Tyler's height is less than his shadow's length so it makes sense that the tree's height is less than the length of its shadow. Check [latex]h={\color{Red}{18}}[/latex] in the original proportion.
[latex]\begin{align*}\frac68&=\frac h{24}\\[2ex]\frac68 &\overset{?}{=} \frac{\color{Red}{18}}{24}\\[2ex]\frac34&=\frac34\checkmark\end{align*}[/latex]
Try It
10) A telephone pole casts a shadow that is [latex]50[/latex] feet long. Nearby, an [latex]8[/latex] foot tall traffic sign casts a shadow that is [latex]10[/latex] feet long. How tall is the telephone pole?
Solution
The telephone pole is [latex]40[/latex] feet tall.
Try It
11) A pine tree casts a shadow of [latex]80[/latex] feet next to a [latex]30[/latex] foot tall building which casts a [latex]40[/latex] feet shadow. How tall is the pine tree?
Solution
The pine tree is [latex]60[/latex] feet tall.
Solve Uniform Motion Applications
We have solved uniform motion problems using the formula [latex]D=rt[/latex] in previous chapters. We used a table like the one below to organize the information and lead us to the equation.
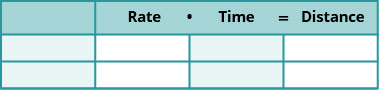
The formula [latex]D=rt[/latex] assumes we know [latex]r[/latex] and [latex]t[/latex] and use them to find [latex]D[/latex]. If we know [latex]D[/latex] and [latex]r[/latex] and need to find [latex]t[/latex], we would solve the equation for [latex]t[/latex] and get the formula [latex]t=\frac{D}{r}[/latex].
We have also explained how flying with or against the wind affects the speed of a plane. We will revisit that idea in the next example.
Example 2.5.5
An airplane can fly [latex]200[/latex] miles into a [latex]30[/latex] mph headwind in the same amount of time it takes to fly [latex]300[/latex] miles with a [latex]30[/latex] mph tailwind. What is the speed of the airplane?
Solution
This is a uniform motion situation. A diagram will help us visualize the situation.

We fill in the chart to organize the information.
Step 1: We are looking for the speed of the airplane.
Let [latex]r=\text{the speed of the airplane.}[/latex]
When the plan flies with the wind, the wind increases its speed and so the rate is [latex]r+30[/latex].
When the plane flies against the wind, the wind decreases its speed and the rate is [latex]r-30[/latex].
Step 2: Write in the rates.
Step 3: Write in the distances.
Since [latex]D=r\cdot t[/latex], we solve for [latex]t[/latex] and get [latex]t=\frac{D}{r}[/latex].
Step 4: We divide the distance by the rate in each row, and place the expression in the time column.
| Rate • Time = Distance | |||
| Headwind | [latex]r-30[/latex] | [latex]\frac{200}{r-30}[/latex] | [latex]200[/latex] |
| Tailwind | [latex]r+30[/latex] | [latex]\frac{300}{r+30}[/latex] | [latex]300[/latex] |
Step 5: We know the times are equal and so we write our equation.
[latex]\frac{200}{r-30}=\frac{300}{r+30}[/latex]
Step 6: We multiply both sides by the LCD.
[latex]\left(r+30\right)\left(r-30\right)\left(\frac{200}{r-30}\right)=\left(r+30\right)\left(r-30\right)\left(\frac{300}{r+30}\right)[/latex]
Step 7: Simplify.
[latex]\begin{align*}&\;&\left(r+30\right)\left(200\right)&=\left(r-30\right)300\\&\;&200r+6000&=300r-9000\\&\text{Solve.}\;\;\;\;\;&15000&=100r\end{align*}[/latex]
Step 8: Check.
Is [latex]150[/latex] mph a reasonable speed for an airplane? Yes.
If the plane is travelling [latex]150[/latex] mph and the wind is [latex]30[/latex] mph,
| Tailwind | [latex]150+30=180\mathrm{mph}[/latex] | [latex]\frac{300}{180}=\frac53\mathrm{hours}[/latex] |
| Headwind | [latex]150-30=120\mathrm{mph}[/latex] | [latex]\frac{200}{120}=\frac53\mathrm{hours}[/latex] |
The times are equal, so it checks.
The plane was travelling [latex]150[/latex] mph.
Try It
12) Link can ride his bike [latex]20[/latex] miles into a [latex]3[/latex] mph headwind in the same amount of time he can ride [latex]30[/latex] miles with a [latex]3[/latex] mph tailwind. What is Link’s biking speed?
Solution
Link’s biking speed is [latex]15[/latex] mph.
Try It
13) Danica can sail her boat [latex]5[/latex] miles into a [latex]7[/latex] mph headwind in the same amount of time she can sail [latex]12[/latex] miles with a [latex]7[/latex] mph tailwind. What is the speed of Danica’s boat without a wind?
Solution
The speed of Danica’s boat is [latex]17[/latex] mph.
In the next example, we will know the total time resulting from travelling different distances at different speeds.
Example 2.5.6
Jazmine trained for [latex]3[/latex] hours on Saturday. She ran [latex]8[/latex] miles and then biked [latex]24[/latex] miles. Her biking speed is [latex]4[/latex] mph faster than her running speed. What is her running speed?
Solution
This is a uniform motion situation. A diagram will help us visualize the situation.

We fill in the chart to organize the information.
Step 1: We are looking for Jazmine’s running speed.
Let [latex]r=\text{Jazmine’s running speed.}[/latex]
Step 2: Her biking speed is [latex]4[/latex] miles faster than her running speed.
[latex]r+4=\text{her biking speed}[/latex]
Step 3: The distances are given, enter them into the chart.
Since [latex]D=r\cdot t[/latex], we solve for [latex]t[/latex] and get [latex]t=\frac{D}{r}[/latex].
Step 4: We divide the distance by the rate in each row, and place the expression in the time column.
| Rate • Time = Distance | |||
| Run | [latex]r[/latex] | [latex]\frac8{r}[/latex] | [latex]8[/latex] |
| Bike | [latex]r+4[/latex] | [latex]\frac{24}{r+4}[/latex] | [latex]24[/latex] |
| [latex]3[/latex] | |||
Step 5: Write a word sentence.
Her time plus the time biking is [latex]3[/latex] hours.
Step 6: Translate the sentence to get the equation.
[latex]\frac{8}{r}+\frac{24}{r+4}=3[/latex]
Step 7: Solve.
[latex]\begin{array}{rcl}r(r+4)\left(\frac8r+\frac{24}{r+24}\right)&=&3\cdot r(r+4)\\8(r+4)+24r&=&3r(r+4)\\8r+32+24r&=&3r^2+12r\\32+32r&=&3r^2+12r\\0&=&3r^2-20r-32\\0&=&(3r+4)(r-8)\end{array}[/latex]
[latex](3r+4)=0,(r-8)=0[/latex]
[latex]\cancel{r=-\frac{4}{3}},r=8[/latex]
Step 8: Check.
A negative speed does not make sense in this problem, so [latex]r=8[/latex] is the solution.
Is [latex]8[/latex] mph a reasonable running speed? Yes.
If Jazmine’s running rate is [latex]4[/latex], then her biking rate,
[latex]r+4[/latex], which is [latex]8+4=12[/latex].
| Run 8 mph | [latex]\frac{8\;\mathrm{miles}}{12\;\mathrm{mph}}=1\;\mathrm{hour}[/latex] |
| Bike 12 mph | [latex]\frac{24\;\mathrm{miles}}{12\;\mathrm{mph}}=2\;\mathrm{hours}[/latex] |
Total [latex]3[/latex] hours.
Jazmine’s running speed is [latex]8[/latex] mph.
Try It
14) Dennis went cross-country skiing for [latex]6[/latex] hours on Saturday. He skied [latex]20[/latex] mile uphill and then [latex]20[/latex] miles back downhill, returning to his starting point. His uphill speed was [latex]5[/latex] mph slower than his downhill speed. What was Dennis’ speed going uphill and his speed going downhill?
Solution
Dennis’s uphill speed was [latex]10[/latex] mph and his downhill speed was [latex]5[/latex] mph.
Try It
15) Joon drove [latex]4[/latex] hours to his home, driving [latex]208[/latex] miles on the interstate and [latex]40[/latex] miles on country roads. If he drove [latex]15[/latex] mph faster on the interstate than on the country roads, what was his rate on the country roads?
Solution
Joon’s rate on the country roads is [latex]50[/latex] mph.
Once again, we will use the uniform motion formula solved for the variable [latex]t[/latex].
Example 2.5.7
Hamilton rode his bike downhill [latex]12[/latex] miles on the river trail from his house to the ocean and then rode uphill to return home. His uphill speed was [latex]8[/latex] miles per hour slower than his downhill speed. It took him [latex]2[/latex] hours longer to get home than it took him to get to the ocean. Find Hamilton’s downhill speed.
Solution
This is a uniform motion situation. A diagram will help us visualize the situation.
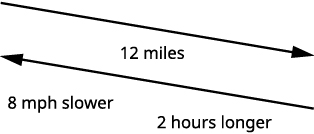
We fill in the chart to organize the information.
Step 1: We are looking for Hamilton’s downhill speed.
Let [latex]h=\text{Hamilton’s downhill speed.}[/latex]
Step 2: His uphill speed is [latex]8[/latex] miles per hour slower.
[latex]h-8=\text{Hamilton’s uphill speed}[/latex]
Step 3: Enter the rates into the chart.
The distance is the same in both directions.
[latex]12[/latex] miles.
Step 4: Since [latex]D=r\cdot t[/latex], we solve for [latex]t[/latex] and get [latex]t=\frac{D}{r}[/latex].
Step 5: We divide the distance by the rate in each row, and place the expression in the time column.
| Rate • Time = Distance | |||
| Downhill | [latex]h[/latex] | [latex]\frac{12}{h}[/latex] | [latex]12[/latex] |
| Uphill | [latex]h-8[/latex] | [latex]\frac{12}{h-8}[/latex] | [latex]12[/latex] |
Step 6: Write a word sentence about the line.
He took [latex]2[/latex] hours longer uphill than downhill.
The uphill time is [latex]2[/latex] more than the downhill time.
Step 7: Translate the sentence to get the equation.
[latex]\frac{12}{h-8}=\frac{12}{h}+2[/latex]
Step 8: Solve.
[latex]\begin{array}{rcl}\frac{12}{h-8}&=&\frac{12}h+2\\h(h-8)\left(\frac{12}{h-8}\right)&=&h(h-8)\left(\frac{12}h+2\right)\\12h&=&12(h-8)+2h(h-8)\\12h&=&12h-96+2h^2-16h\\0&=&2h^2-16h-96\\0&=&2(h^2-8h-48)\\0&=&2(h-12)(h+4)\end{array}[/latex]
[latex]h-12=0[/latex], [latex]h+4=0[/latex]
[latex]h=12[/latex], [latex]\cancel{h=-4}[/latex]
Step 9: Check.
Is [latex]12[/latex] mph a reasonable speed for biking downhill? Yes.
| Downhill | [latex]12\;\mathrm{mph}[/latex] | [latex]\frac{12\;\mathrm{miles}}{12\;\mathrm{mph}}=1\;\mathrm{hour}[/latex] |
|---|---|---|
| Uphill | [latex]12-8=4\;\mathrm{mph}[/latex] | [latex]\frac{12\;\mathrm{miles}}{4\;\mathrm{mph}}=3\;\mathrm{hours}[/latex] |
The uphill time is [latex]2[/latex] hours more that the downhill time.
Hamilton’s downhill speed is [latex]12[/latex] mph.
Try It
16) Kayla rode her bike [latex]75[/latex] miles home from college one weekend and then rode the bus back to college. It took her [latex]2[/latex] hours less to ride back to college on the bus than it took her to ride home on her bike, and the average speed of the bus was [latex]10[/latex] miles per hour faster than Kayla’s biking speed. Find Kayla’s biking speed.
Solution
Kayla’s biking speed was [latex]15[/latex] mph.
Try It
17) Victoria jogs [latex]12[/latex] miles to the park along a flat trail and then returns by jogging on an [latex]20[/latex] mile hilly trail. She jogs [latex]1[/latex] mile per hour slower on the hilly trail than on the flat trail, and her return trip takes her two hours longer. Find her rate of jogging on the flat trail.
Solution
Victoria jogged [latex]6[/latex] mph on the flat trail.
Solve Work Applications
The weekly gossip magazine has a big story about the Princess’ baby and the editor wants the magazine to be printed as soon as possible. She has asked the printer to run an extra printing press to get the printing done more quickly. Press #1 takes 6 hours to do the job and Press #2 takes 12 hours to do the job. How long will it take the printer to get the magazine printed with both presses running together?
This is a typical ‘work’ application. There are three quantities involved here—the time it would take each of the two presses to do the job alone and the time it would take for them to do the job together.
If Press #1 can complete the job in 6 hours, in one hour it would complete [latex]\frac{1}{6}[/latex] of the job.
If Press #2 can complete the job in 12 hours, in one hour it would complete [latex]\frac{1}{12}[/latex] of the job.
We will let [latex]t[/latex] be the number of hours it would take the presses to print the magazines with both presses running together. So in [latex]1[/latex] hour working together they have completed [latex]\frac{1}{t}[/latex] of the job.
We can model this with the word equation and then translate to a rational equation. To find the time it would take the presses to complete the job if they worked together, we solve for [latex]t[/latex].
A chart will help us organize the information. We are looking for how many hours it would take to complete the job with both presses running together.
Step 1: Let [latex]t=\text{the number of hours needed to complete the job together}[/latex].
Step 2: Enter the hours per job for Press #1, Press #2, and when they work together.
If a job on Press #1 takes [latex]6[/latex] hours, then in 1 hour [latex]\frac{1}{6}[/latex] of the job is completed.
Similarly find the part of the job completed/hours for Press #2 and when they're both running together.
| Number of hours to complete the job. | Part of the job completed/hour | |
| Press #1 | [latex]6[/latex] | [latex]\frac16[/latex] |
| Press #2 | [latex]12[/latex] | [latex]\frac1{12}[/latex] |
| Together | [latex]t[/latex] | [latex]\frac1{t}[/latex] |
Step 3: Write a word sentence.
The part completed by Press #1 plus the part completed by Press #2 equals the amount completed together.
Step 4: Translate into an equation.
Work completed by
[latex]\begin{array}{c} {\color{Blue}{\underbrace{{\color{Black}{\text{Press #1}+\text{Press #2}=\text{Together}}}}}}\\ \frac16+\frac1{12}=\frac1{t} \end{array}[/latex]
Step 5: Solve.
[latex]\frac16+\frac1{12}=\frac1{t}[/latex]
Step 6: Multiply by the LCD, [latex]12t[/latex]
[latex]12t\left(\frac16+\frac1{12}\right)=12t\left(\frac1{t}\right)[/latex]
Step 7: Simplify.
[latex]\begin{align*}2t+t&=12\\3t&=12\\t&=4\end{align*}[/latex]
When both presses are running it takes [latex]4[/latex] hours to do the job.
Keep in mind, it should take less time for two presses to complete a job working together than for either press to do it alone.
Example 2.5.8
Suppose Pete can paint a room in [latex]10[/latex] hours. If he works at a steady pace, in [latex]1[/latex] hour he would paint [latex]\frac{1}{10}[/latex] of the room. If Alicia would take [latex]8[/latex] hours to paint the same room, then in [latex]1[/latex] hour she would paint [latex]\frac{1}{8}[/latex] of the room. How long would it take Pete and Alicia to paint the room if they worked together (and didn’t interfere with each other’s progress)?
Solution
This is a ‘work’ application. A chart will help us organize the information. We are looking for the numbers of hours it will take them to paint the room together.
In one hour Pete did [latex]\frac{1}{10}[/latex] of the job. Alicia did [latex]\frac{1}{8}[/latex] of the job. And together they did [latex]\frac{1}{t}[/latex] of the job.
Step 1: Let [latex]t[/latex] be the number of hours needed to paint the room together.
Step 2: Enter the hours per job for Pete, Alicia, and when they work together.
In [latex]1[/latex] hour working together, they have completed [latex]\frac{1}{t}[/latex] of the job.
Similarly, find the part of the job completed/hour by Pete and then by Alicia.
| Number of complete hours to the job. | Part of job completed/hour | |
|---|---|---|
| Pete | [latex]10[/latex] | [latex]\frac1{10}[/latex] |
| Alicia | [latex]8[/latex] | [latex]\frac18[/latex] |
| Together | [latex]t[/latex] | [latex]\frac1{t}[/latex] |
Step 3: Write a word sentence.
The work completed by Pete plus the work completed by Alicia equals the total work completed.
Work completed by:
[latex]\begin{array}{c} {\color{Teal}{\underbrace{{\color{Black}{\text{Pete}+\text{Alicia}=\text{Together}}}}}}\\\frac1{10}=+\frac18=\frac1{t}\end{array}[/latex]
Step 4: Multiply by the LCD, [latex]40t[/latex].
[latex]{\color{Red}{40t}}\left(\frac1{10}+\frac18\right)={\color{Red}{40t}}\left(\frac1{t}\right)[/latex]
Step 5: Distribute.
[latex]{\color{Red}{40t}}\cdot\frac1{10}+{\color{Red}{40t}}\cdot\frac18={\color{Red}{40t}}\left(\frac1{t}\right)[/latex]
Step 6: Simplify and solve.
[latex]\begin{align*}4t+5t&=40\\9t&=40\\t&=\frac{40}{9}\end{align*}[/latex]
Step 7: We’ll write as a mixed number so that we can convert it to hours and minutes.
[latex]t=4\frac49\;\mathrm{hours}[/latex]
Step 8: Remember, [latex]1[/latex] hour = [latex]60[/latex] minutes.
[latex]t=4\;\mathrm{hours}=\frac49(60\;\mathrm{minutes})[/latex]
Step 9: Multiply, and then round to the nearest minute.
[latex]t=4\;\mathrm{hours}+27\;\mathrm{minutes}[/latex]
It would take Pete and Alicia about [latex]4[/latex] hours and [latex]27[/latex] minutes to paint the room.
Try It
18) One gardener can mow a golf course in [latex]4[/latex] hours, while another gardener can mow the same golf course in [latex]6[/latex] hours. How long would it take if the two gardeners worked together to mow the golf course?
Solution
When the two gardeners work together it takes [latex]2[/latex] hours and [latex]24[/latex] minutes.
Try It
19) Daria can weed the garden in [latex]7[/latex] hours, while her mother can do it in [latex]3[/latex]. How long will it take the two of them working together?
Solution
When Daria and her mother work together it takes [latex]2[/latex] hours and [latex]6[/latex] minutes.
Example 2.5.9
Ra’shon can clean the house in [latex]7[/latex] hours. When his sister helps him it takes [latex]3[/latex] hours. How long does it take his sister when she cleans the house alone?
Solution
This is a work problem. A chart will help us organize the information.
We are looking for how many hours it would take Ra’shon’s sister to complete the job by herself.
Step 1: Let [latex]s[/latex] be the number of hours Ra’shon’s sister takes to clean the house alone.
Step 2: Enter the hours per job for Ra’shon, his sister, and when they work together.
If Ra’shon takes [latex]7[/latex] hours, then in [latex]1[/latex] hour [latex]\frac{1}{7}[/latex] of the job is completed.
If Ra’shon’s sister takes [latex]s[/latex] hours, then in [latex]1[/latex] hour [latex]\frac{1}{s}[/latex] of the job is completed.
| Number of hours to clean the house | Part of the job completed/hour | |
| Ra'shon | [latex]7[/latex] | [latex]\frac17[/latex] |
| His sister | [latex]s[/latex] | [latex]\frac1{s}[/latex] |
| Together | [latex]3[/latex] | [latex]\frac13[/latex] |
Step 3: Write a word sentence.
The part completed by Ra’shon plus the part by his sister equals the amount completed together.
Step 4: Translate to an equation.
Work completed by:
[latex]\begin{array}{c} {\color{Teal}{\underbrace{{\color{Black}{\text{Ra'shon}+\text{His sister}=\text{Together}}}}}}\\\frac17+\frac1{s}=\frac13\end{array}[/latex]
Step 5: Solve.
[latex]\frac17+\frac1{s}=\frac13[/latex]
Step 6: Multiply by the LCD, [latex]21[/latex].
[latex]21s\left(\frac17+\frac1{s}\right)=\left(\frac13\right)21s[/latex]
Step 7: Simplify.
[latex]\begin{align*}-4s&=-21\\s&=\frac{-21}{-4}\\&=\frac{21}{4}\end{align*}[/latex]
Step 8: Write as a mixed number to convert it to hours and minutes.
[latex]s=5\frac14\;\mathrm{hours}[/latex]
There are [latex]60[/latex] minutes in [latex]1[/latex] hour.
[latex]\begin{align*}s&=5\;\mathrm{hours}+\frac14(60\;\mathrm{minutes})\\s&=5\;\mathrm{hours}+15\;\mathrm{minutes}\end{align*}[/latex]
It would take Ra’shon’s sister [latex]5[/latex] hours and [latex]15[/latex] minutes to clean the house alone.
Try It
20) Alice can paint a room in [latex]6[/latex] hours. If Kristina helps her it takes them [latex]4[/latex] hours to paint the room. How long would it take Kristina to paint the room by herself?
Solution
Kristina can paint the room in [latex]12[/latex] hours.
Try It
21) Tracy can lay a slab of concrete in [latex]3[/latex] hours, with Jordan’s help they can do it in [latex]2[/latex] hours. If Jordan works alone, how long will it take?
Solution
It will take Jordan [latex]6[/latex] hours.
Solve Direct Variation Problems
When two quantities are related by a proportion, we say they are proportional to each other. Another way to express this relation is to talk about the variation of the two quantities. We will discuss direct variation and inverse variation in this section.
Lindsay gets paid [latex]\$15[/latex] per hour at her job. If we let [latex]s[/latex] be her salary and [latex]h[/latex] be the number of hours she has worked, we could model this situation with the equation [latex]s=15h[/latex]
Lindsay’s salary is the product of a constant, [latex]15[/latex], and the number of hours she works. We say that Lindsay’s salary varies directly with the number of hours she works. Two variables vary directly if one is the product of a constant and the other.
Direct Variation
For any two variables [latex]x[/latex] and [latex]y[/latex], [latex]y[/latex] varies directly with [latex]x[/latex] if [latex]y=kx[/latex], where [latex]k\neq0[/latex]
The constant [latex]k[/latex] is called the constant of variation.
In applications using direct variation, generally we will know values of one pair of the variables and will be asked to find the equation that relates [latex]x[/latex] and [latex]y[/latex]. Then we can use that equation to find values of [latex]y[/latex] for other values of [latex]x[/latex].
We’ll list the steps here.
HOW TO
Solve direct variation problems.
- Write the formula for direct variation.
- Substitute the given values for the variables.
- Solve for the constant of variation.
- Write the equation that relates [latex]x[/latex] and [latex]y[/latex] using the constant of variation.
Now we’ll solve an application of direct variation.
Example 2.5.10
When Raoul runs on the treadmill at the gym, the number of calories, [latex]c[/latex], he burns varies directly with the number of minutes, [latex]m[/latex], he uses the treadmill. He burned [latex]315[/latex] calories when he used the treadmill for [latex]18[/latex] minutes.
a. Write the equation that relates [latex]c[/latex] and [latex]m[/latex].
b. How many calories would he burn if he ran on the treadmill for [latex]25[/latex] minutes?
Solution
a. The number of calories, [latex]c[/latex], varies directly with the number of minutes, [latex]m[/latex], on the treadmill, and [latex]c=315[/latex] when [latex]m=18[/latex].
Step 1: Write the formula for direct variation.
[latex]y=kx[/latex]
Step 2: We will use [latex]c[/latex] in place of [latex]y[/latex] and [latex]m[/latex] in place of [latex]x[/latex].
[latex]c=km[/latex]
Step 2: Substitute the given values for the variables.
[latex]{\color{Red}{315}}=k\cdot{\color{Red}{18}}[/latex]
Step 3: Solve for the constant of variation.
[latex]\begin{align*}\frac{315}{18}&=\frac{k\cdot{\color{Red}{18}}}{18}\\17.5&=k\end{align*}[/latex]
Step 4: Write the equation that relates [latex]c[/latex] and [latex]m[/latex].
[latex]c=km[/latex]
Step 5: Substitute in the constant of variation.
[latex]c=17.5m[/latex]
b. Find [latex]c[/latex] when [latex]m=25[/latex].
Step 1: Write the equation that relates [latex]c[/latex] and [latex]m[/latex].
[latex]c=17.5m[/latex]
Step 2: Substitute the given value for [latex]m[/latex].
[latex]c=17.5({\color{Red}{25}})[/latex]
Step 3: Simplify.
[latex]c=437.5[/latex]
Raoul would burn [latex]437.5[/latex] calories if he used the treadmill for [latex]25[/latex] minutes.
Try It
22) The number of calories, [latex]c[/latex], burned varies directly with the amount of time, [latex]t[/latex], spent exercising. Arnold burned [latex]312[/latex] calories in [latex]65[/latex] minutes exercising.
a. Write the equation that relates [latex]c[/latex] and [latex]t[/latex].
b. How many calories would he burn if he exercises for [latex]90[/latex] minutes?
Solution
a. [latex]c=4.8t[/latex]
b. He would burn [latex]432[/latex] calories.
Try It
23) The distance a moving body travels, [latex]d[/latex], varies directly with time, [latex]t[/latex], it moves. A train travels [latex]100[/latex] miles in [latex]2[/latex] hours
a. Write the equation that relates [latex]d[/latex] and [latex]t[/latex].
b. How many miles would it travel in [latex]5[/latex] hours?
Solution
a. [latex]d=50t[/latex]
b. It would travel [latex]250[/latex] miles.
Solve Inverse Variation Problems
Many applications involve two variable that vary inversely. As one variable increases, the other decreases. The equation that relates them is [latex]y=\frac{k}{x}[/latex].
Inverse Variation
For any two variables [latex]x[/latex] and [latex]y[/latex], [latex]y[/latex] varies inversely with [latex]x[/latex] if [latex]y=\frac{k}{x}[/latex], where [latex]k\neq0[/latex]
The constant [latex]k[/latex] is called the constant of variation.
The word ‘inverse’ in inverse variation refers to the multiplicative inverse. The multiplicative inverse of [latex]x[/latex] is [latex]\frac{1}{x}[/latex].
We solve inverse variation problems in the same way we solved direct variation problems. Only the general form of the equation has changed. We will copy the procedure box here and just change ‘direct’ to ‘inverse’.
HOW TO
Solve inverse variation problems.
- Write the formula for inverse variation.
- Substitute the given values for the variables.
- Solve for the constant of variation.
- Write the equation that relates [latex]x[/latex] and [latex]y[/latex] using the constant of variation.
Example 2.5.11
The frequency of a guitar string varies inversely with its length. A [latex]26[/latex] in.-long string has a frequency of [latex]440[/latex] vibrations per second.
a. Write the equation of variation.
b. How many vibrations per second will there be if the string’s length is reduced to [latex]20[/latex] inches by putting a finger on a fret?
Solution
a. The frequency varies inversely with the length.
Step 1: Name the variables.
Let [latex]f=\mathrm{frequency}[/latex].
Let [latex]L=\mathrm{length}[/latex].
Step 2: Write the formula for inverse variation.
[latex]y=\frac{k}{x}[/latex]
Step 3: We will use [latex]f[/latex] in place of [latex]y[/latex] and [latex]L[/latex] in place of [latex]x[/latex].
[latex]f=\frac{k}{L}[/latex]
Step 4: Substitute the given values for the variables.
[latex]\begin{align*}f&={\color{Blue}{440}}\text{ when }L={\color{Red}{26}}\\{\color{Blue}{440}}&=\frac{k}{\color{Red}{26}}\end{align*}[/latex]
Step 5: Solve for the constant of variation
[latex]\begin{align*}26(440)&=26\left(\frac{k}{26}\right)\\11,440&=k\end{align*}[/latex]
Step 6: Write the equation that relates [latex]f[/latex] and [latex]L[/latex].
[latex]f=\frac{k}{L}[/latex]
Step 7: Substitute the constant of variation
[latex]f=\frac{11,440}{L}[/latex]
b. Find [latex]f[/latex] when [latex]L=20[/latex].
Step 1: Write the equation that relates [latex]f[/latex] and [latex]L[/latex].
[latex]f=\frac{11,440}{L}[/latex]
Step 2: Substitute the given value for [latex]L[/latex].
[latex]f=\frac{11,440}{20}[/latex]
Step 3: Simplify.
[latex]f=572[/latex]
A [latex]20[/latex]-inch guitar string has a frequency of [latex]572[/latex] vibrations per second.
Try It
24) The number of hours it takes for ice to melt varies inversely with the air temperature. Suppose a block of ice melts in [latex]2[/latex] hours when the temperature is [latex]65[/latex] degrees Celsius.
a. Write the equation of variation.
b. How many hours would it take for the same block of ice to melt if the temperature was [latex]78[/latex] degrees?
Solution
a. [latex]h=\frac{130}{t}[/latex]
b. [latex]1\frac{2}{3}[/latex] hours
Try It
25) Xander’s new business found that the daily demand for its product was inversely proportional to the price, [latex]p[/latex]. When the price is [latex]\$5[/latex], the demand is [latex]700[/latex] units.
a. Write the equation of variation.
b. What is the demand if the price is raised to [latex]\$7[/latex]?
Solution
a. [latex]x=\frac{3500}{p}[/latex]
b. [latex]500[/latex] units
Access this online resource for additional instruction and practice with applications of rational expressions
Key Concepts
- A proportion is an equation of the form [latex]\frac{a}{b}=\frac{c}{d}[/latex], where [latex]b\neq0,d\neq0[/latex]. The proportion is read “[latex]a[/latex] is to [latex]b[/latex] as [latex]c[/latex] is to [latex]d[/latex].”
- Property of Similar Triangles
If [latex]\triangle ABC[/latex] is similar to [latex]\triangle XYZ[/latex],
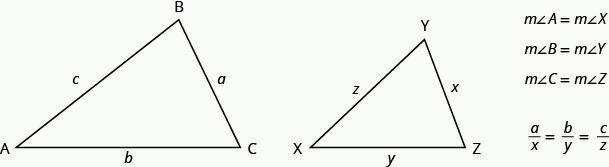
Figure 2.5.11 - then their corresponding angle measure are equal and their corresponding sides have the same ratio.
- Direct Variation
- For any two variables [latex]x[/latex] and [latex]y[/latex], [latex]y[/latex] varies directly with [latex]x[/latex] if [latex]y=kx[/latex], where [latex]k\neq0[/latex]. The constant [latex]k[/latex] is called the constant of variation.
- How to solve direct variation problems.
- Write the formula for direct variation.
- Substitute the given values for the variables.
- Solve for the constant of variation.
- Write the equation that relates [latex]x[/latex] and [latex]y[/latex].
- Inverse Variation
- For any two variables [latex]x[/latex] and [latex]y[/latex], [latex]y[/latex] varies inversely with [latex]x[/latex] if [latex]y=\frac{k}{x}[/latex], where [latex]k\neq0[/latex]. The constant [latex]k[/latex] is called the constant of variation.
- How to solve inverse variation problems.
- Write the formula for inverse variation.
- Substitute the given values for the variables.
- Solve for the constant of variation.
- Write the equation that relates [latex]x[/latex] and [latex]y[/latex].
Self Check
a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
b) After looking at the checklist, do you think you are well-prepared for the next section? Why or why not?
Glossary
- proportion
- When two rational expressions are equal, the equation relating them is called a proportion.
- similar figures
- Two figures are similar if the measures of their corresponding angles are equal and their corresponding sides have the same ratio.
When two rational expressions are equal, the equation relating them is called a proportion.
Two figures are similar if the measures of their corresponding angles are equal and their corresponding sides have the same ratio.

