1.3 Factor Special Products
Learning Objectives
By the end of this section, you will be able to:
- Factor perfect square trinomials
- Factor differences of squares
- Factor sums and differences of cubes
Try It
Before you get started, take this readiness quiz:
1) Simplify: [latex]{\left(3{x}^{2}\right)}^{3}[/latex].
2) Multiply: [latex]{\left(m+4\right)}^{2}[/latex].
3) Multiply: [latex]\left(x-3\right)\left(x+3\right)[/latex].
We have seen that some binomials and trinomials result from special products—squaring binomials and multiplying conjugates. If you learn to recognize these kinds of polynomials, you can use the special products patterns to factor them much more quickly.
Factor Perfect Square Trinomials
Some trinomials are perfect squares. They result from multiplying a binomial times itself. We squared a binomial using the Binomial Squares pattern in a previous chapter.
[latex]\overset{\color{Red}{(a+b)^2}}{(3x+4)^2}[/latex]
[latex]\overset{\color{Red} \;\;a^2\;\;\;+\;\;\;2\;\cdot\;a\;\;\;\cdot\;b\;\;\;+\;\;\;b^2}{(3x)^2+2(3x\cdot 4)+4^2}[/latex]
[latex]9x^2+24x+16[/latex]
The trinomial [latex]9{x}^{2}+24x+16[/latex] is called a perfect square trinomial. It is the square of the binomial [latex]3x+4[/latex].
In this chapter, you will start with a perfect square trinomial and factor it into its prime factors.
You could factor this trinomial using the methods described in the last section, since it is of the form [latex]a{x}^{2}+bx+c[/latex]. But if you recognize that the first and last terms are squares and the trinomial fits the perfect square trinomials pattern, you will save yourself a lot of work.
Here is the pattern—the reverse of the binomial squares pattern.
Perfect Square Trinomials Pattern
If [latex]a[/latex] and [latex]b[/latex] are real numbers
To make use of this pattern, you have to recognize that a given trinomial fits it. Check first to see if the leading coefficient is a perfect square, [latex]{a}^{2}[/latex]. Next check that the last term is a perfect square, [latex]{b}^{2}[/latex]. Then check the middle term—is it the product, [latex]2ab[/latex]? If everything checks, you can easily write the factors.
Example 1.3.1
How to Factor Perfect Square Trinomials
Factor: [latex]9{x}^{2}+12x+4[/latex].
Solution
Is the last term a perfect square? Write is as a square, [latex]b^2[/latex].
Check the middle term. Is it [latex]2ab[/latex]?
Try It
4) Factor: [latex]4{x}^{2}+12x+9[/latex].
Solution
[latex]{\left(2x+3\right)}^{2}[/latex]
Try It
5) Factor: [latex]9{y}^{2}+24y+16[/latex].
Solution
[latex]{\left(3y+4\right)}^{2}[/latex]
The sign of the middle term determines which pattern we will use. When the middle term is negative, we use the pattern [latex]{a}^{2}-2ab+{b}^{2}[/latex], which factors to [latex]{\left(a-b\right)}^{2}[/latex].
The steps are summarized here.
HOW TO
Factor Perfect Square Trinomials
[latex]\begin{array}{cccccccc}\mathbf{\text{Step 1:}}\hfill & \text{Does the trinomial fit the pattern?}\hfill & & & \hfill {a}^{2}+2ab+{b}^{2}\hfill & & & \hfill {a}^{2}-2ab+{b}^{2}\hfill \\ & \text{Is the first term a perfect square?}\hfill & & & \hfill {\left(a\right)}^{2}\hfill & & & \hfill {\left(a\right)}^{2}\hfill \\ & \text{Write it as a square.}\hfill & & & & & & \\ & \text{Is the last term a perfect square?}\hfill & & & \hfill {\left(b\right)}^{2}\hfill & & & \hfill {\left(b\right)}^{2}\hfill \\ & \text{Write it as a square.}\hfill & & & & & & \\ & \text{Check the middle term. Is it }2ab?\hfill & & & \hfill {\left(a\right)}^{2}\searrow\underset{2\cdot a\cdot b}{}\swarrow{\left(b\right)}^{2}\hfill & & & \hfill {\left(a\right)}^{2}\searrow\underset{2\cdot a\cdot b}{}\swarrow{\left(b\right)}^{2}\hfill \\ \mathbf{\text{Step 2:}}\hfill & \text{Write the square of the binomial.}\hfill & & & \hfill {\left(a+b\right)}^{2}\hfill & & & \hfill {\left(a-b\right)}^{2}\hfill \\ \mathbf{\text{Step 3:}}\hfill & \text{Check by multiplying.}\hfill & & & & & & \end{array}[/latex]
We’ll work one now where the middle term is negative.
Example 1.3.2
Factor: [latex]81y^2 - 72y + 16[/latex]
Solution
The first and last terms are squares. See if the middle term fits the pattern of a perfect square trinomial. The middle term is negative, so the binomial square would be [latex]{\left(a-b\right)}^{2}[/latex].
Step 1: Are the first and last terms perfect squares?
Check the middle term.
[latex](9y^2) (4^2)[/latex]
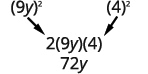
Step 2: Does it match [latex](a-b)^2[/latex]?
Yes.
[latex]\overset{\color{Red} \;\;a^2\;\;\;+\;\;\;2\;\cdot\;a\;\;\;\cdot\;b\;\;\;+\;\;b^2}{(9y)^2-2\cdot9y\cdot4+4^2}[/latex]
Step 3: Write as the square of a binomial.
[latex](9y - 4)^2[/latex]
Step 4: Check by multiplying.
[latex]\begin{eqnarray*}&=&{(9y-4)}^2\\&=&{(9y)}^2-2\times9y\times4+4^2\\&=&81y^2-72y+16\;\checkmark\end{eqnarray*}[/latex]
Try It
6) Factor: [latex]64{y}^{2}-80y+25[/latex].
Solution
[latex]{\left(8y-5\right)}^{2}[/latex]
Try It
7) Factor: [latex]16{z}^{2}-72z+81[/latex].
Solution
[latex]{\left(4z-9\right)}^{2}[/latex]
The next example will be a perfect square trinomial with two variables.
Example 1.3.3
Factor: [latex]36x^2 + 84xy + 49y^2[/latex].
Solution
Step 1: Test each term to verify the pattern.
[latex]\overset{\color{Red} \;\;a^2\;\;\;+\;\;\;2\;\cdot\;a\;\;\cdot\;b\;\;\;+\;\;b^2}{(6x)^2+2\cdot6x\cdot7y+(7y)^2}[/latex]
Step 2: Factor.
[latex](6x+7y)^2[/latex]
Step 3: Check by multiplying.
[latex]\begin{eqnarray*}&=&{(6x+7y)}^2\\&=&{(6x)}^2+2\times6x\times7y+{(7y)}^2\\&=&36x^2+84xy+49y^2\;\checkmark\end{eqnarray*}[/latex]
Try It
8) Factor: [latex]49{x}^{2}+84xy+36{y}^{2}[/latex].
Solution
[latex]{\left(7x+6y\right)}^{2}[/latex]
Try It
9) Factor: [latex]64{m}^{2}+112mn+49{n}^{2}[/latex].
Solution
[latex]{\left(8m+7n\right)}^{2}[/latex]
Remember the first step in factoring is to look for a greatest common factor. Perfect square trinomials may have a GCF in all three terms and it should be factored out first. And, sometimes, once the GCF has been factored, you will recognize a perfect square trinomial.
Example 1.3.4
Factor: [latex]100x^2y-80xy+16y[/latex].
Solution
Step 1: Is there a GCF?
Yes, [latex]4y[/latex], so factor it out.
[latex]4y(25x^2-20x+4)[/latex]
Step 2: Is this a perfect square trinomial?
Verify the pattern.
[latex]\overset{\color{Red} \;\;a^2\;\;\;+\;\;\;2\;\cdot\;a\;\;\;\cdot\;b\;\;\;+\;\;b^2}{4y\left[(5x)^2-2\cdot5x \cdot2+2^2\right]}[/latex]
Step 3: Factor.
[latex]4y(5x-2)^2[/latex]
Remember: Keep the factor [latex]4y[/latex] in the final product.
Step 5: Check.
[latex]\begin{eqnarray*}&=&4y\left(5x-2\right)^2\\&=&4y\left[\left(5x\right)^2-2\cdot5x\cdot2+2^2\right]\\&=&4y\left(25x^2-20x+4\right)\\&=&100x^2y-80xy+16y\;\checkmark\end{eqnarray*}[/latex]
Try It
10) Factor: [latex]8{x}^{2}y-24xy+18y[/latex].
Solution
[latex]2y{\left(2x-3\right)}^{2}[/latex]
Try It
11) Factor: [latex]27{p}^{2}q+90pq+75q[/latex].
Solution
[latex]3q{\left(3p+5\right)}^{2}[/latex]
Factor Differences of Squares
The other special product you saw in the previous chapter was the Product of Conjugates pattern. You used this to multiply two binomials that were conjugates. Here’s an example:
[latex]\begin{eqnarray*}&=&\overset{\color{red}{(a\;-\;b)\;\;\;(a\;+\;b)}}{(3x-4)(3x+4)}\\&=&\overset{\color{red}{(a)^2\;\;-\;\;(b)^2}}{(3x)^2-(4)^2}\\&=&9x^2-16\\\end{eqnarray*}[/latex]
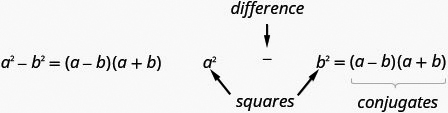
A difference of squares factors to a product of conjugates.
Remember, “difference” refers to subtraction. So, to use this pattern you must make sure you have a binomial in which two squares are being subtracted.
Example 1.3.5
How to Factor a Trinomial Using the Difference of Squares
Factor: [latex]64{y}^{2}-1[/latex].
Solution
Is this a difference?
Yes.
[latex]64y^2{\color{Red} -}1[/latex]
Are the first and last terms perfect squares?
Yes.
Step 2: Write them as squares.
Write them as [latex]x^2[/latex] and [latex]2^2[/latex].
[latex]\overset{\color{Red}{a^2\;\;-\;\;b^2}}{(8y)^2-1^2}[/latex]
Step 3: Write the product of conjugates.
[latex]\overset{\color{Red}{(a\;-\;b)\;\;\;(a\;+\;b)}}{(8y-1)(8y+1)}[/latex]
Step 4: Check.
[latex]\begin{eqnarray*}&=&(8y-1)(8y+1)\\&=&64y^2-1\;\checkmark\end{eqnarray*}[/latex]
Try It
12) Factor: [latex]121{m}^{2}-1[/latex].
Solution
[latex]\left(11m-1\right)\left(11m+1\right)[/latex]
Try It
13) Factor: [latex]81{y}^{2}-1[/latex].
Solution
[latex]\left(9y-1\right)\left(9y+1\right)[/latex]
HOW TO
Factor Differences of Squares
[latex]\begin{array}{ccccc}\mathbf{\text{Step 1:}}\hfill & \text{Does the binomial fit the pattern?}\hfill & & & \hfill {a}^{2}-{b}^{2}\hfill \\ & \text{Is this a difference?}\hfill & & & \hfill \text{____}-\text{____}\hfill \\ & \text{Are the first and last terms perfect squares?}\hfill & & & \\ \mathbf{\text{Step 2:}}\hfill & \text{Write them as squares.}\hfill & & & \hfill {\left(a\right)}^{2}-{\left(b\right)}^{2}\hfill \\ \mathbf{\text{Step 3:}}\hfill & \text{Write the product of conjugates.}\hfill & & & \hfill \left(a-b\right)\left(a+b\right)\hfill \\ \mathbf{\text{Step 4:}}\hfill & \text{Check by multiplying.}\hfill & & & \end{array}[/latex]
It is important to remember that sums of squares do not factor into a product of binomials. There are no binomial factors that multiply together to get a sum of squares. After removing any GCF, the expression [latex]{a}^{2}+{b}^{2}[/latex] is prime!
The next example shows variables in both terms.
Example 1.3.6
Factor: [latex]144x^2-49y^2[/latex].
Solution
Step 1: Is this a difference of squares?
Yes.
[latex](12x)^2-(7y)^2[/latex]
Step 2: Factor as the product of conjugates.
[latex](12x-7y)(12x+7y)[/latex]
Step 3: Check by multiplying.
[latex]\begin{eqnarray*}&=&(12x-7y)(12x+7y)\\&=&144x^2-49y^2\;\checkmark\end{eqnarray*}[/latex]
Try It
14) Factor: [latex]196{m}^{2}-25{n}^{2}[/latex].
Solution
[latex]\left(16m-5n\right)\left(16m+5n\right)[/latex]
Try It
15) Factor: [latex]121{p}^{2}-9{q}^{2}[/latex].
Solution
[latex]\left(11p-3q\right)\left(11p+3q\right)[/latex]
As always, you should look for a common factor first whenever you have an expression to factor. Sometimes a common factor may “disguise” the difference of squares and you won’t recognize the perfect squares until you factor the GCF.
Also, to completely factor the binomial in the next example, we’ll factor a difference of squares twice!
Example 1.3.7
Factor: [latex]48x^4 y^2-243y^2[/latex].
Solution
Step 1: Is there a GCF?
Yes, [latex]3y^2[/latex]—factor it out!
[latex]3y^2(16x^4-81)[/latex]
Step 2: Is the binomial a difference of squares?
Yes.
[latex]3y^2\left((4x^2)2-(9)^2)\right)[/latex]
Step 3: Factor as a product of conjugates.
[latex]3y^2(4x^2-9)(4x^2+9)[/latex]
Step 4: Notice the first binomial is also a difference of squares!
[latex]3y^2\left((2x)^2-(3)^2\right)(4x^2+9)[/latex]
Step 5: Factor it as the product of conjugates.
[latex]3y^2(2x-3)(2x+3)(4x^2+9)[/latex]
The last factor, the sum of squares, cannot be factored.
Step 6: Check by multiplying.
[latex]\begin{eqnarray*}&=&3y^2\left(2x-3\right)\left(2x+3\right)\left(4x^2+9\right)\\&=&3y^2\left(4x^2-9\right)\left(4x^2+9\right)\\&=&3y^2\left(16x^4-81\right)\\&=&48x^4y^2-243y^2\;\checkmark\end{eqnarray*}[/latex]
Try It
16) Factor: [latex]2{x}^{4}{y}^{2}-32{y}^{2}[/latex].
Solution
[latex]2{y}^{2}\left(x-2\right)\left(x+2\right)\left({x}^{2}+4\right)[/latex]
Try It
17) Factor: [latex]7{a}^{4}{c}^{2}-7{b}^{4}{c}^{2}[/latex].
Solution
[latex]7{c}^{2}(a-b)(a+b)({a}^{2}+{b}^{2})[/latex]
The next example has a polynomial with 4 terms. So far, when this occurred we grouped the terms in twos and factored from there. Here we will notice that the first three terms form a perfect square trinomial.
Example 1.3.8
Factor: [latex]x^2-6x+9-y^2[/latex].
Solution
Step 1: Notice that the first three terms form a perfect square trinomial. Factor by grouping the first three terms.
[latex]\underbrace{x^2-6x+9}-y^2[/latex]
Step 2: Use the perfect square trinomial pattern.
[latex](x-3)^2-y^2[/latex]
Step 3: Is this a difference of squares?
Yes—write them as squares.
[latex]\overset{\color{Red}{a^2\;\;-\;\;b^2}}{(x-3)^2-y^2}[/latex]
Step 4: Factor as the product of conjugates.
[latex]\overset{\color{Red}{(a\;\;-\;\;b)\;\;(x\;\;+\;\;b)}}{\left((x-3)-y\right)\left(x-3)+y\right)}[/latex]
Step 5: Factor as the product of conjugates.
[latex](x-3-y)(x-3+y)[/latex]
You may want to rewrite the solution as [latex](x-y-3)(x+y-3)[/latex].
Try It
18) Factor: [latex]{x}^{2}-10x+25-{y}^{2}[/latex].
Solution
[latex]\left(x-5-y\right)\left(x-5+y\right)[/latex]
Try It
19) Factor: [latex]{x}^{2}+6x+9-4{y}^{2}[/latex].
Solution
[latex]\left(x+3-2y\right)\left(x+3+2y\right)[/latex]
Factor Sums and Differences of Cubes
There is another special pattern for factoring, one that we did not use when we multiplied polynomials. This is the pattern for the sum and difference of cubes. We will write these formulas first and then check them by multiplication.
We’ll check the first pattern and leave the second to you.
| [latex]{\color{Red}{(a+b)}}(a^2-ab+b^2)[/latex] | |
| Distribute. | [latex]{\color{Red} a}(a^2-ab+b^2)+{\color{Red} b}(a^2-ab+b^2)[/latex] |
| Multiply. | [latex]a^3-a^2b+ab^2+a^2b-ab^2+b^3[/latex] |
| Combine like terms. | [latex]a^3+b^3[/latex] |
Sum and Difference of Cubes Pattern
The two patterns look very similar, don’t they? But notice the signs in the factors. The sign of the binomial factor matches the sign in the original binomial. And the sign of the middle term of the trinomial factor is the opposite of the sign in the original binomial. If you recognize the pattern of the signs, it may help you memorize the patterns.
[latex]{a^3}{\color{Green}{\underset{\text{opposite signs}}{\underbrace{{\color{Red}{\underset{\text{same sign}}{\underbrace{+{\color{Black}{b^3=(a}+}}}}}{\color{Black}{b)(a^2}-}}}}}{ab+b^2)}[/latex]
[latex]{a^3}{\color{Green}{\underset{\text{opposite signs}}{\underbrace{{\color{Red}{\underset{\text{same sign}}{\underbrace{-{\color{Black}{b^3=(a}-}}}}}{\color{Black}{b)(a^2}+}}}}}{ab+b^2)}[/latex]
The trinomial factor in the sum and difference of cubes pattern cannot be factored.
It be very helpful if you learn to recognize the cubes of the integers from 1 to 10, just like you have learned to recognize squares. We have listed the cubes of the integers from 1 to 10.
| [latex]n[/latex] | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| [latex]{n}^{3}[/latex] | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 | 1000 |
Example 1.3.9
How to Factor the Sum or Difference of Cubes
Factor: [latex]{x}^{3}+64[/latex].
Solution
Step 1: Does the binomial fit the sum or difference of cubes pattern?
Is it a sum or a difference?
[latex]x^3{\color{Red} +}64[/latex]
This is a sum.
Are the first and last terms perfect cubes?
Yes.
Step 2: Write the terms as cubes.
Write them as [latex]x^3[/latex] and [latex]4^3[/latex].
[latex]\overset{\color{Red}{a^3\;+\;b^3}}{x^3+4^3}[/latex]
Step 3: Use either the sum or difference of cubes pattern.
This is a sum of cubes.
[latex]\overset{\color{Red}{(a\;+\;b)}}{(x+4)}\overset{\color{Red} (a^2\;-\;ab\;+\;b^2)}{(x^2-4x+4^2)}[/latex]
Step 4: Simplify inside the parentheses.
It is already simplified.
[latex](x+4)(x^2-4x+4^2)[/latex]
Step 5: Check by multiplying the factors.
[latex]\begin{array}{rcl}x^2-4x&+&16\\x&+&4\\\hline4x^2-16x&+&64\checkmark\\x^3-4x^2+16x&&\\\hline x^3\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;&+&64\end{array}[/latex]
Try It
20) Factor: [latex]{x}^{3}+27[/latex].
Solution
[latex]\left(x+3\right)\left({x}^{2}-3x+9\right)[/latex]
Try It
21) Factor: [latex]{y}^{3}+8[/latex].
Solution
[latex]\left(y+2\right)\left({y}^{2}-2y+4\right)[/latex]
HOW TO
Factor the Sum or Difference of Cubes
- Does the binomial fit the sum or difference of cubes pattern?
Is it a sum or difference?
Are the first and last terms perfect cubes?
- Write them as cubes.
- Use either the sum or difference of cubes pattern.
- Simplify inside the parentheses.
- Check by multiplying the factors.
Example 1.3.10
Factor: [latex]27u^3 - 125v^3[/latex].
Solution
Step 1: Does the binomial fit the sum or difference of cubes pattern?
This binomial is a difference. The first and last terms are perfect cubes.
Step 2: Write the terms as cubes.
[latex]\overset{\color{Red}{a^3\;\;-\;\;b^3}}{(3u)^3-(5v)^3}[/latex]
Step 3: Use the difference of cubes pattern.
[latex]\overset{\color{Red}{(a\;\;-\;\;b)}}{(3u-5v)}\overset{\color{Red}{(a^2\;\;+\;ab\;\;+\;\;b^2)}}{\left((3u)^2+3u\cdot5v+(5v)^2\right)}[/latex]
Step 4: Simplify.
[latex]\overset{\color{Red} (a\;\;-\;\;b)}{(3u-5v)}\overset{\color{Red}{(a^2\;\;+\;ab\;\;+\;\;b^2)}}{(9u^2+15uv+25v^2)}[/latex]
Step 5: Check by multiplying.
We’ll leave the check to you.
Try It
22) Factor: [latex]8{x}^{3}-27{y}^{3}[/latex].
Solution
[latex]\left(2x-3y\right)\left(4{x}^{2}-6xy+9{y}^{2}\right)[/latex]
Try It
23) Factor: [latex]1000{m}^{3}-125{n}^{3}[/latex].
Solution
[latex]\left(10m-5n\right)\left(100{m}^{2}-50mn+25{n}^{2}\right)[/latex]
In the next example, we first factor out the GCF. Then we can recognize the sum of cubes.
Example 1.3.11
Factor: [latex]6x^3y + 48y^4[/latex].
Solution
Step 1: Factor the common factor.
[latex]6y(x^3 + 8y^3)[/latex]
Step 2: Does the binomial fit the sum or difference of cubes pattern?
This binomial is a sum. The first and last terms are perfect cubes.
Step 3: Write the terms as cubes.
[latex]6y\overset{\color{Red}{(a^3\;\;+\;\;b^3)}}{\left(x^3+(2y)^3\right)}[/latex]
Step 4: Use the sum of cubes pattern.
[latex]6y\overset{\color{Red}{(a\;\;+\;\;b)}}{(x+2y)}\overset{\color{Red}{(a^2\;\;-\;\;ab\;\;+\;\;b^2)}}{\left(x^2-x\cdot2y+(2y)^2\right)}[/latex]
Step 5: Simplify.
[latex]6y(x+2y)(x^2-2xy+4y^2)[/latex]
Step 6: Check.
To check, you may find it easier to multiply the sum of cubes factors first, then multiply that product by [latex]6y[/latex]. We’ll leave the multiplication for you.
Try It
24) Factor: [latex]500{p}^{3}+4{q}^{3}[/latex].
Solution
[latex]4\left(5p+q\right)\left(25{p}^{2}-5pq+{q}^{2}\right)[/latex]
Try It
25) Factor: [latex]432{c}^{3}+686{d}^{3}[/latex].
Solution
[latex]2\left(6c+7d\right)\left(36{c}^{2}-42cd+49{d}^{2}\right)[/latex]
The first term in the next example is a binomial cubed.
Example 1.3.12
Factor: [latex](x + 5)^3 - 64x^3[/latex].
Solution
Step 1: Does the binomial fit the sum or difference of cubes pattern?
This binomial is a difference. The first and last terms are perfect cubes.
Step 2: Write the terms as cubes.
[latex]\overset{\color{Red}{a^3\;\;-\;\;b^3}}{(x+5)^3-(4x)^3}[/latex]
Step 3: Use the difference of cubes pattern.
[latex]\overset{\color{Red}{(a\;\;-\;\;b)}}{\left((x+5)-4x\right)}\overset{\color{Red}{(a^2\;\;+\;ab\;\;+\;\;b^2)}}{\left((x+5)^2+(x+5)\cdot4x+(4x)^2\right)}[/latex]
Step 4: Simplify.
[latex]\begin{eqnarray*}&=&(x+5-4x)(x^2+10x+25+4x^2+20x+16x^2)\\&=&(-3x+5)(21x^2+30x+25)\end{eqnarray*}[/latex]
Step 5: Check by multiplying.
We’ll leave the check to you.
Try It
26) Factor: [latex]{\left(y+1\right)}^{3}-27{y}^{3}[/latex].
Solution
[latex]\left(-2y+1\right)\left(13{y}^{2}+5y+1\right)[/latex]
Try It
27) Factor: [latex]{\left(n+3\right)}^{3}-125{n}^{3}[/latex].
Solution
[latex]\left(-4n+3\right)\left(31{n}^{2}+21n+9\right)[/latex]
Access this online resource for additional instruction and practice with factoring special products.
Key Concepts
- Perfect Square Trinomials Pattern: If [latex]a[/latex] and [latex]b[/latex] are real numbers,
[latex]\begin{array}{c}\hfill {a}^{2}+2ab+{b}^{2}={\left(a+b\right)}^{2}\hfill \\ \hfill {a}^{2}-2ab+{b}^{2}={\left(a-b\right)}^{2}\hfill \end{array}[/latex]
- How to factor perfect square trinomials.
[latex]\begin{array}{cccccccc}\mathbf{\text{Step 1:}}\hfill & \text{Does the trinomial fit the pattern?}\hfill & & & \hfill {a}^{2}+2ab+{b}^{2}\hfill & & & \hfill {a}^{2}-2ab+{b}^{2}\hfill \\ & \text{Is the first term a perfect square?}\hfill & & & \hfill {\left(a\right)}^{2}\hfill & & & \hfill {\left(a\right)}^{2}\hfill \\ & \text{Write it as a square.}\hfill & & & & & & \\ & \text{Is the last term a perfect square?}\hfill & & & \hfill {\left(a\right)}^{2}{\left(b\right)}^{2}\hfill & & & \hfill {\left(a\right)}^{2}{\left(b\right)}^{2}\hfill \\ & \text{Write it as a square.}\hfill & & & & & & \\ & \text{Check the middle term. Is it }2ab?\hfill & & & \hfill {\left(a\right)}^{2}\searrow\underset{2\cdot a\cdot b}{}\swarrow{\left(b\right)}^{2}\hfill & & & \hfill {\left(a\right)}^{2}\searrow\underset{2\cdot a\cdot b}{}\swarrow{\left(b\right)}^{2}\hfill \\ \mathbf{\text{Step 2:}}\hfill & \text{Write the square of the binomial.}\hfill & & & \hfill {\left(a+b\right)}^{2}\hfill & & & \hfill {\left(a-b\right)}^{2}\hfill \\ \mathbf{\text{Step 3:}}\hfill & \text{Check by multiplying.}\hfill & & & & & & \end{array}[/latex]
- Difference of Squares Pattern: If [latex]a[/latex], [latex]b[/latex] are real numbers,
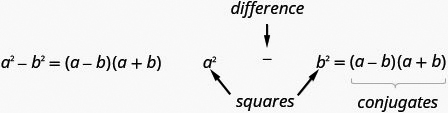
Figure 1.3.4 - How to factor differences of squares.
[latex]\begin{array}{ccccc}\text{Step 1:}\hfill & \text{Does the binomial fit the pattern?}\hfill & & & \hfill {a}^{2}-{b}^{2}\hfill \\ & \text{Is this a difference?}\hfill & & & \hfill \text{____}-\text{____}\hfill \\ & \text{Are the first and last terms perfect squares?}\hfill & & & \\ \text{Step 2:}\hfill & \text{Write them as squares.}\hfill & & & \hfill {\left(a\right)}^{2}-{\left(b\right)}^{2}\hfill \\ \text{Step 3:}\hfill & \text{Write the product of conjugates.}\hfill & & & \hfill \left(a-b\right)\left(a+b\right)\hfill \\ \text{Step 4:}\hfill & \text{Check by multiplying.}\hfill & & & \end{array}[/latex]
- Sum and Difference of Cubes Pattern
[latex]\begin{array}{c}\hfill {a}^{3}+{b}^{3}=\left(a+b\right)\left({a}^{2}-ab+{b}^{2}\right)\hfill \\ \hfill {a}^{3}-{b}^{3}=\left(a-b\right)\left({a}^{2}+ab+{b}^{2}\right)\hfill \end{array}[/latex] - How to factor the sum or difference of cubes.
- Does the binomial fit the sum or difference of cubes pattern?
Is it a sum or difference?Are the first and last terms perfect cubes? - Write them as cubes.
- Use either the sum or difference of cubes pattern.
- Simplify inside the parentheses
- Check by multiplying the factors.
- Does the binomial fit the sum or difference of cubes pattern?
Self Check
After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.