4.7 Graph Quadratic Functions Using Transformations
Learning Objectives
By the end of this section, you will be able to:
- Graph quadratic functions of the form [latex]f\left(x\right)={x}^{2}+k[/latex]
- Graph quadratic functions of the form [latex]f\left(x\right)={\left(x-h\right)}^{2}[/latex]
- Graph quadratic functions of the form [latex]f\left(x\right)=a{x}^{2}[/latex]
- Graph quadratic functions using transformations
- Find a quadratic function from its graph
Try It
Before you get started, take this readiness quiz:
1) Graph the function [latex]f\left(x\right)={x}^{2}[/latex] by plotting points.
2) Factor completely: [latex]{y}^{2}-14y+49[/latex].
3) Factor completely: [latex]2{x}^{2}-16x+32[/latex].
Graph Quadratic Functions of the form [latex]f(x)=x^2+k[/latex]
In the last section, we learned how to graph quadratic functions using their properties. Another method involves starting with the basic graph of [latex]f\left(x\right)={x}^{2}[/latex] and ‘moving’ it according to information given in the function equation. We call this graphing quadratic functions using transformations.
In the first example, we will graph the quadratic function [latex]f\left(x\right)={x}^{2}[/latex] by plotting points. Then we will see what effect adding a constant, [latex]k[/latex], to the equation will have on the graph of the new function [latex]f(x)=x^2+k[/latex].
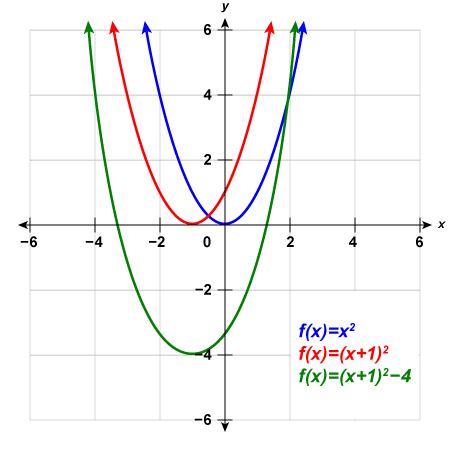
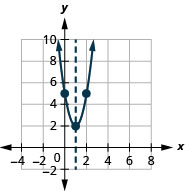
Example 4.7.1
Graph [latex]f(x)=x^2[/latex], [latex]g(x)=x^2+2[/latex], and [latex]h(x)=x^2-2[/latex] on the same rectangular coordinate system. Describe what effect adding a constant to the function has on the basic parabola.
Solution
Step 1: Plotting points will help us see the effect of the constants on the basic [latex]f\left(x\right)={x}^{2}[/latex] graph.
We fill in the chart for all three functions.
| [latex]x[/latex] | [latex]{\color{blue}{\boldsymbol f}}{\color{blue}{\mathbf(}}{\color{blue}{\boldsymbol x}}{\color{blue}{\mathbf)}}{\color{blue}{\mathbf=}}{\color{blue}{\boldsymbol x}}^{\color{blue}{\mathbf2}}[/latex] | [latex]{\color{blue}{\mathbf(}}{{\color{blue}{\boldsymbol x}}{\color{blue}{\mathbf,}}{\color{blue}{\boldsymbol f}}{\color{blue}{\mathbf(}}{\color{blue}{\boldsymbol x}}{\color{blue}{\mathbf)}}}{\color{blue}{\mathbf)}}{}[/latex] | [latex]{\color{red}{\boldsymbol g}}{{\color{red}{\mathbf(}}{\color{red}{\boldsymbol x}}{\color{red}{\mathbf)}}{\color{red}{\mathbf=}}{\color{red}{\boldsymbol x}}^{\color{red}{\mathbf2}}{\color{red}{\mathbf+}}}{\color{red}{\mathbf2}}{}[/latex] | [latex]{\color{red}{\mathbf(}}{{\color{red}{\boldsymbol x}}{\color{red}{\mathbf,}}{\color{red}{\boldsymbol g}}{\color{red}{\mathbf(}}{\color{red}{\boldsymbol x}}{\color{red}{\mathbf)}}}{\color{red}{\mathbf)}}{}[/latex] | [latex]{\bf{\color{green}{h}}{\color{green}{(}}{\color{green}{x}}{\color{green}{)=(}}{\color{green}{x}}{\color{green}{+1)}}^{\color{green}{2}}}[/latex] | [latex]{\color{green}{\mathbf(}}{{\color{green}{\boldsymbol x}}{\color{green}{\mathbf,}}{\color{green}{\boldsymbol h}}{\color{green}{\mathbf(}}{\color{green}{\boldsymbol x}}{\color{green}{\mathbf)}}}{\color{green}{\mathbf)}}{}[/latex] |
|---|---|---|---|---|---|---|
| [latex]-3[/latex] | [latex]9[/latex] | [latex](-3,9)[/latex] | [latex]9+2[/latex] | [latex](-3,11)[/latex] | [latex]9-2[/latex] | [latex](-3,7)[/latex] |
| [latex]-2[/latex] | [latex]4[/latex] | [latex](-2,4)[/latex] | [latex]4+2[/latex] | [latex](-2,6)[/latex] | [latex]4-2[/latex] | [latex](-2,2)[/latex] |
| [latex]-1[/latex] | [latex]1[/latex] | [latex](-1,1)[/latex] | [latex]1+2[/latex] | [latex](-1,3)[/latex] | [latex]1-2[/latex] | [latex](-1,1)[/latex] |
| [latex]0[/latex] | [latex]0[/latex] | [latex](0,0)[/latex] | [latex]0+2[/latex] | [latex](0,2)[/latex] | [latex]0-2[/latex] | [latex](0,-2)[/latex] |
| [latex]1[/latex] | [latex]1[/latex] | [latex](1,1)[/latex] | [latex]1+2[/latex] | [latex](1,3)[/latex] | [latex]1-2[/latex] | [latex](1,-1)[/latex] |
| [latex]2[/latex] | [latex]4[/latex] | [latex](2,4)[/latex] | [latex]4+2[/latex] | [latex](2,6)[/latex] | [latex]4-2[/latex] | [latex](2,2)[/latex] |
| [latex]3[/latex] | [latex]9[/latex] | [latex](3,9)[/latex] | [latex]9+2[/latex] | [latex](3,11)[/latex] | [latex]9-2[/latex] | [latex](3,7)[/latex] |
Step 2: The [latex]g(x)[/latex] values are two more than the [latex]f(x)[/latex] values. Also, the [latex]h(x)[/latex] values are two less than the [latex]f(x)[/latex] values. Now we will graph all three functions on the same rectangular coordinate system.
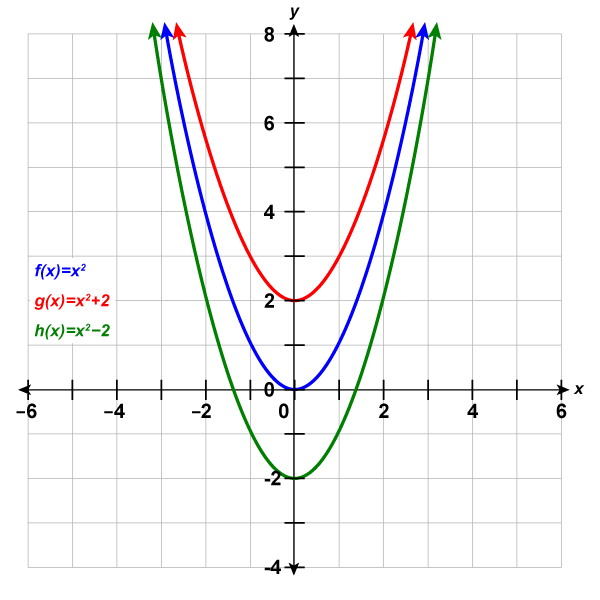
The graph of [latex]{\color{red}{g}}{{\color{red}{\left(x\right)}}{\color{red}{=}}{\color{red}{x}}^{\color{red}{2}}{\color{red}{+}}}{\color{red}{2}}[/latex] is the same as the graph of [latex]{\color{blue}{f}}{\color{blue}{\left(x\right)}}{\color{blue}{=}}{\color{blue}{x}}^{\color{blue}{2}}[/latex] but shifted up [latex]2[/latex] units.
The graph of [latex]{\color{green}{h}}{{\color{green}{\left(x\right)}}{\color{green}{=}}{\color{green}{x}}^{\color{green}{2}}{\color{green}{-}}}{\color{green}{2}}[/latex] is the same as the graph of [latex]{\color{blue}{f}}{\color{blue}{\left(x\right)}}{\color{blue}{=}}{\color{blue}{x}}^{\color{blue}{2}}[/latex] but shifted down [latex]2[/latex] units.
Try It
4) Complete the following:
a. Graph [latex]f\left(x\right)={x}^{2}[/latex], [latex]g\left(x\right)={x}^{2}+1[/latex], and [latex]h\left(x\right)={x}^{2}-1[/latex] on the same rectangular coordinate system.
b. Describe what effect adding a constant to the function has on the basic parabola.
Solution
a.
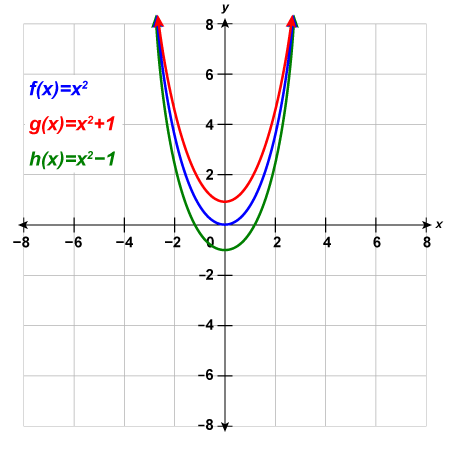
b. The graph of [latex]g\left(x\right)={x}^{2}+1[/latex] is the same as the graph of [latex]f\left(x\right)={x}^{2}[/latex] but shifted up [latex]1[/latex] unit. The graph of [latex]h\left(x\right)={x}^{2}-1[/latex] is the same as the graph of [latex]f\left(x\right)={x}^{2}[/latex] but shifted down [latex]1[/latex] unit.
Try It
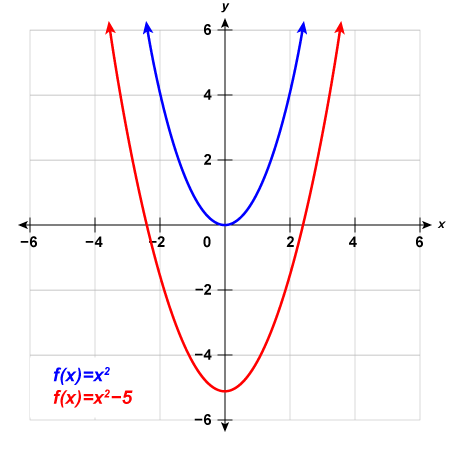
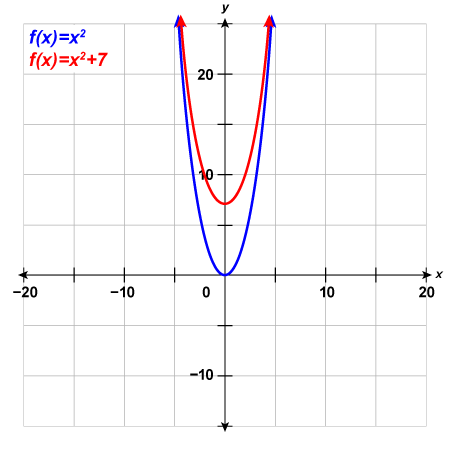
5) Complete the following:
a. Graph [latex]f\left(x\right)={x}^{2}[/latex], [latex]g\left(x\right)={x}^{2}+6[/latex], and [latex]h\left(x\right)={x}^{2}-6[/latex] on the same rectangular coordinate system.
b. Describe what effect adding a constant to the function has on the basic parabola.
Solution
a.
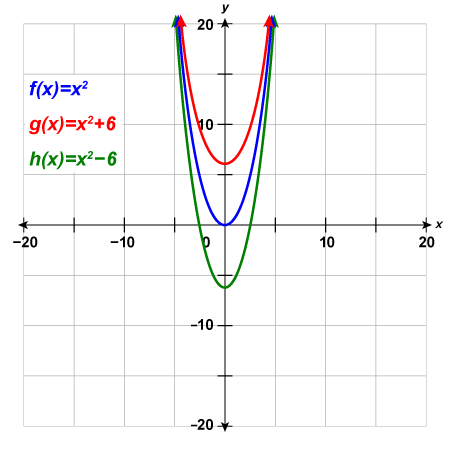
b. The graph of [latex]h\left(x\right)={x}^{2}+6[/latex] is the same as the graph of [latex]f\left(x\right)={x}^{2}[/latex] but shifted up [latex]6[/latex] units. The graph of [latex]h\left(x\right)={x}^{2}-6[/latex] is the same as the graph of [latex]f\left(x\right)={x}^{2}[/latex] but shifted down [latex]6[/latex] units.
The last example shows us that to graph a quadratic function of the form [latex]f\left(x\right)={x}^{2}+k[/latex], we take the basic parabola graph of [latex]f\left(x\right)={x}^{2}[/latex] and vertically shift it up [latex]\left(k>0\right)[/latex] or shift it down [latex]\left(k<0\right)[/latex].
This transformation is called a vertical shift.
HOW TO
Graph a Quadratic Function of the form [latex]f\left(x\right)={x}^{2}+k[/latex] Using a Vertical Shift
The graph of [latex]f\left(x\right)={x}^{2}+k[/latex] shifts the graph of [latex]f\left(x\right)={x}^{2}[/latex] vertically [latex]k[/latex] units.
-
- If [latex]k>0[/latex], shift the parabola vertically up [latex]k[/latex] units.
- If [latex]k<0[/latex], shift the parabola vertically down [latex]|k|[/latex] units.
Now that we have seen the effect of the constant, [latex]k[/latex], it is easy to graph functions of the form [latex]f\left(x\right)={x}^{2}+k[/latex]. We just start with the basic parabola of [latex]f\left(x\right)={x}^{2}[/latex] and then shift it up or down.
It may be helpful to practice sketching [latex]f\left(x\right)={x}^{2}[/latex] quickly. We know the values and can sketch the graph from there.
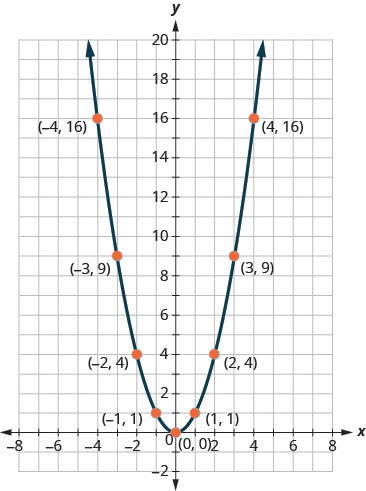
Once we know this parabola, it will be easy to apply the transformations. The next example will require a vertical shift.
Example 4.7.2
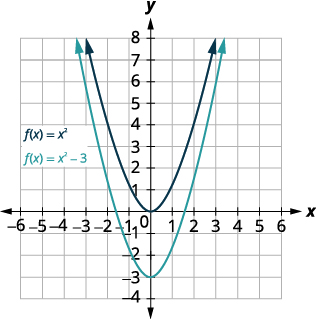
Graph [latex]f\left(x\right)={x}^{2}-3[/latex] using a vertical shift.
Solution
Step 1: We first draw the graph of [latex]f\left(x\right)={x}^{2}[/latex] on the grid.
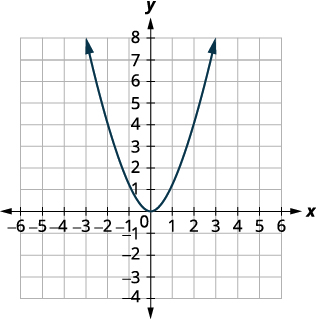
Step 2: Determine [latex]k[/latex].
[latex]{\color{red}{f}}{{\color{red}{(}}{\color{red}{x}}{\color{red}{)}}{\color{red}{=}}{\color{red}{x}}^{\color{red}{2}}{\color{red}{-}}}{\color{red}{3}}[/latex]
State [latex]k[/latex].
[latex]k=-3[/latex]
Step 4: Shift the graph [latex]f\left(x\right)={x}^{2}[/latex] down [latex]3[/latex].
Try It
Graph Quadratic Functions of the form [latex]f(x)=(x-h)^2[/latex]
In the first example, we graphed the quadratic function [latex]f\left(x\right)={x}^{2}[/latex] by plotting points and then saw the effect of adding a constant [latex]k[/latex] to the function had on the resulting graph of the new function [latex]f\left(x\right)={x}^{2}+k[/latex].
We will now explore the effect of subtracting a constant, [latex]h[/latex], from [latex]x[/latex] has on the resulting graph of the new function [latex]f\left(x\right)={\left(x-h\right)}^{2}[/latex].
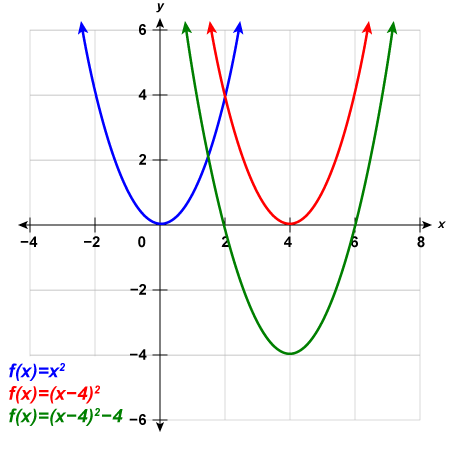
Example 4.7.3
Graph [latex]f\left(x\right)={x}^{2}[/latex], [latex]g\left(x\right)={\left(x-1\right)}^{2}[/latex], and [latex]h\left(x\right)={\left(x+1\right)}^{2}[/latex] on the same rectangular coordinate system. Describe what effect adding a constant to the function has on the basic parabola.
Solution
Step 1: Plotting points will help us see the effect of the constants on the basic [latex]f\left(x\right)={x}^{2}[/latex] graph. We fill in the chart for all three functions.
| [latex]x[/latex] | [latex]{\color{blue}{f}}{\color{blue}{(}}{\color{blue}{x}}{\color{blue}{)}}{\color{blue}{=}}{\color{blue}{x}}^{\color{blue}{2}}[/latex] | [latex]{\color{blue}{(}}{{\color{blue}{x}}{\color{blue}{,}}{\color{blue}{f}}{\color{blue}{(}}{\color{blue}{x}}{\color{blue}{)}}}{\color{blue}{)}}[/latex] | [latex]{\color{red}{g}}{\color{red}{(}}{\color{red}{x}}{\color{red}{)}}{\color{red}{=}}{\color{red}{\left(x-1\right)}}^{\color{red}{2}}[/latex] | [latex]{\color{red}{(}}{{\color{red}{x}}{\color{red}{,}}{\color{red}{g}}{\color{red}{(}}{\color{red}{x}}{\color{red}{)}}}{\color{red}{)}}{}[/latex] | [latex]{\color{green}{h}}{\color{green}{(}}{\color{green}{x}}{\color{green}{)}}{\color{green}{=}}{{\color{green}{(}}{\color{green}{x}}{\color{green}{+}}{\color{green}{1}}{\color{green}{)}}}^{\color{green}{2}}{}[/latex] | [latex]{\color{green}{(}}{{\color{green}{x}}{\color{green}{,}}{\color{green}{h}}{\color{green}{(}}{\color{green}{x}}{\color{green}{)}}}{\color{green}{)}}{}[/latex] |
|---|---|---|---|---|---|---|
| [latex]-3[/latex] | [latex]9[/latex] | [latex](-3,9)[/latex] | [latex]16[/latex] | [latex](-3,16)[/latex] | [latex]4[/latex] | [latex](-3,4)[/latex] |
| [latex]-2[/latex] | [latex]4[/latex] | [latex](-2,4)[/latex] | [latex]9[/latex] | [latex](-2,9)[/latex] | [latex]1[/latex] | [latex](-2,1)[/latex] |
| [latex]-1[/latex] | [latex]1[/latex] | [latex](-1,1)[/latex] | [latex]4[/latex] | [latex](-1,4)[/latex] | [latex]0[/latex] | [latex](-1,0)[/latex] |
| [latex]0[/latex] | [latex]0[/latex] | [latex](0,0)[/latex] | [latex]1[/latex] | [latex](0,1)[/latex] | [latex]1[/latex] | [latex](0,1)[/latex] |
| [latex]1[/latex] | [latex]1[/latex] | [latex](1,1)[/latex] | [latex]0[/latex] | [latex](1,0)[/latex] | [latex]4[/latex] | [latex](1,4)[/latex] |
| [latex]2[/latex] | [latex]4[/latex] | [latex](2,4)[/latex] | [latex]1[/latex] | [latex](2,1)[/latex] | [latex]9[/latex] | [latex](2,9)[/latex] |
| [latex]3[/latex] | [latex]9[/latex] | [latex](3,9)[/latex] | [latex]4[/latex] | [latex](3,4)[/latex] | [latex]16[/latex] | [latex](3,16)[/latex] |
Step 2: The [latex]g(x)[/latex] values and the [latex]h(x)[/latex] values share the common numbers [latex]0[/latex], [latex]1[/latex], [latex]4[/latex], [latex]9[/latex], and [latex]16[/latex], but are shifted.
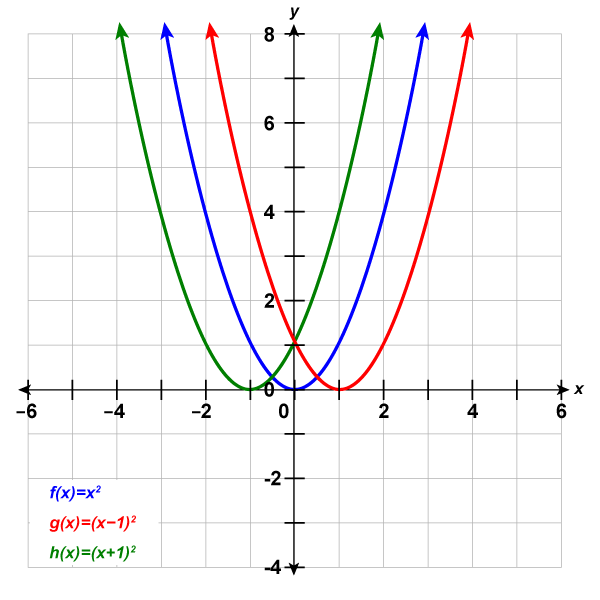
The graph of [latex]{\color{red}{g}}{{\color{red}{(}}{\color{red}{x}}{\color{red}{)}}{\color{red}{=}}{\color{red}{(}}{\color{red}{x}}{\color{red}{-}}{\color{red}{1}}}{\color{red}{)^2}}[/latex] is the same as the graph of [latex]{\color{blue}{f}}{\color{blue}{(}}{\color{blue}{x}}{\color{blue}{)}}{\color{blue}{=}}{\color{blue}{x}}^{\color{blue}{2}}[/latex] but shifted right [latex]1[/latex] unit.
The graph of [latex]{\color{green}{h}}{{\color{green}{(}}{\color{green}{x}}{\color{green}{)}}{\color{green}{=}}{\color{green}{(}}{\color{green}{x}}{\color{green}{+}}{\color{green}{1}}}{\color{green}{)^2}}[/latex] is the same as the graph of [latex]{\color{blue}{f}}{\color{blue}{(}}{\color{blue}{x}}{\color{blue}{)}}{\color{blue}{=}}{\color{blue}{x}}^{\color{blue}{2}}[/latex] but shifted left [latex]1[/latex] unit.
Try It
8) Complete the following:
a. Graph [latex]f\left(x\right)={x}^{2},\phantom{\rule{0.5em}{0ex}}g\left(x\right)={\left(x+2\right)}^{2}[/latex], and [latex]h\left(x\right)={\left(x-2\right)}^{2}[/latex] on the same rectangular coordinate system.
b. Describe what effect adding a constant to the function has on the basic parabola.
Solution
a.
b.
The graph of [latex]g\left(x\right)={\left(x+2\right)}^{2}[/latex] is the same as the graph of [latex]f\left(x\right)={x}^{2}[/latex] but shifted left [latex]2[/latex] units.
The graph of [latex]h\left(x\right)={\left(x-2\right)}^{2}[/latex] is the same as the graph of [latex]f\left(x\right)={x}^{2}[/latex] but shift right [latex]2[/latex] units.
Try It
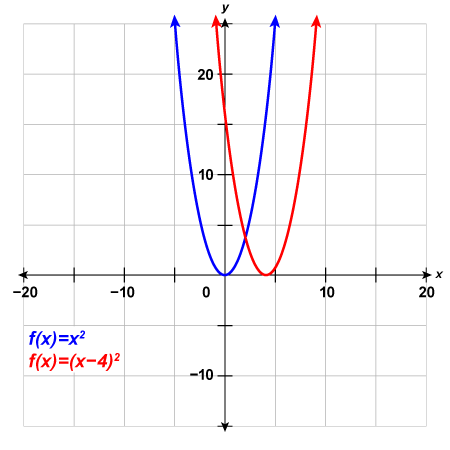
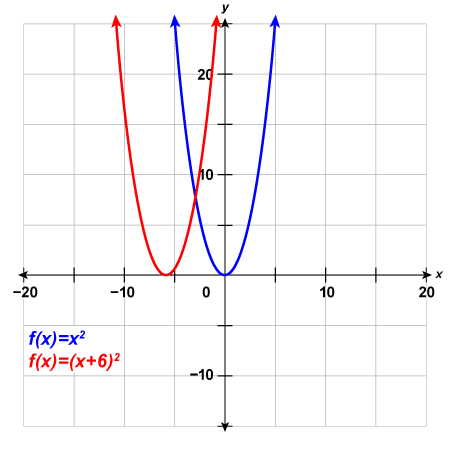
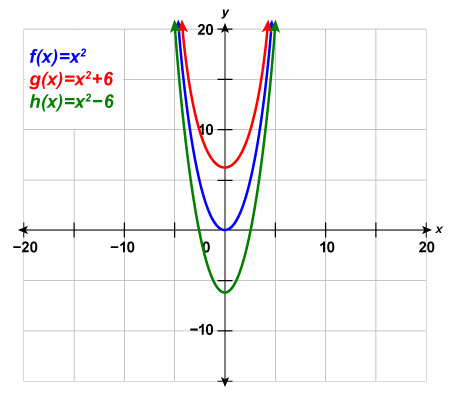
9) Complete the following:
a. Graph [latex]f\left(x\right)={x}^{2}[/latex], [latex]g\left(x\right)={x}^{2}+5[/latex], and [latex]h\left(x\right)={x}^{2}-5[/latex] on the same rectangular coordinate system.
b. Describe what effect adding a constant to the function has on the basic parabola.
Solution
a.
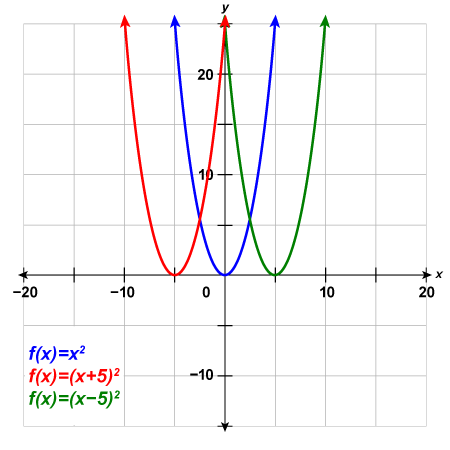
b.
The graph of [latex]g\left(x\right)={\left(x+5\right)}^{2}[/latex] is the same as the graph of [latex]f\left(x\right)={x}^{2}[/latex] but shifted left [latex]5[/latex] units.
The graph of [latex]h\left(x\right)={\left(x-5\right)}^{2}[/latex] is the same as the graph of [latex]f\left(x\right)={x}^{2}[/latex] but shifted right [latex]5[/latex] units.
The last example shows us that to graph a quadratic function of the form [latex]f\left(x\right)={\left(x-h\right)}^{2}[/latex], we take the basic parabola graph of [latex]f\left(x\right)={x}^{2}[/latex] and shift it left ([latex]h>0[/latex]) or shift it right ([latex]h<0[/latex]).
This transformation is called a horizontal shift.
HOW TO
Graph a Quadratic Function of the form [latex]f\left(x\right)={\left(x-h\right)}^{2}[/latex] Using a Horizontal Shift
The graph of [latex]f\left(x\right)={\left(x-h\right)}^{2}[/latex] shifts the graph of [latex]f\left(x\right)={x}^{2}[/latex] horizontally [latex]h[/latex] units.
- If [latex]h>0[/latex], shift the parabola horizontally left [latex]h[/latex] units.
- If [latex]h<0[/latex], shift the parabola horizontally right [latex]|h|[/latex] units.
Now that we have seen the effect of the constant, [latex]h[/latex], it is easy to graph functions of the form [latex]f\left(x\right)={\left(x-h\right)}^{2}[/latex]. We just start with the basic parabola of [latex]f\left(x\right)={x}^{2}[/latex] and then shift it left or right.
The next example will require a horizontal shift.
Example 4.7.4
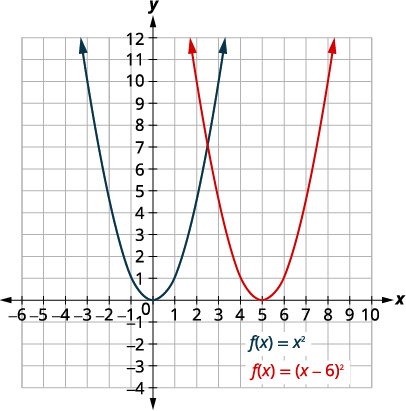
Graph [latex]f\left(x\right)={\left(x-6\right)}^{2}[/latex] using a horizontal shift.
Solution
Step 1: We first draw the graph of [latex]f\left(x\right)={x}^{2}[/latex] on the grid.
![graph of [latex]fx={x}^{2}[/latex]](https://ecampusontario.pressbooks.pub/app/uploads/sites/2897/2022/09/CNX_IntAlg_Figure_09_07_008a_img.jpg)
Step 2: Determine [latex]h[/latex].
[latex]{\color{red}{f}}{\color{red}{(}}{\color{red}{x}}{\color{red}{)}}{\color{red}{=}}{\color{red}{{(x-6)}}}^{\color{red}{2}}[/latex]
State [latex]h[/latex].
[latex]h=6[/latex]
Step 3: Shift the graph [latex]f\left(x\right)={x}^{2}[/latex] to the right [latex]6[/latex] units.
Now that we know the effect of the constants [latex]h[/latex] and [latex]k[/latex], we will graph a quadratic function of the form [latex]f\left(x\right)={\left(x-h\right)}^{2}+k[/latex] by first drawing the basic parabola and then making a horizontal shift followed by a vertical shift. We could do the vertical shift followed by the horizontal shift, but most students prefer the horizontal shift followed by the vertical.
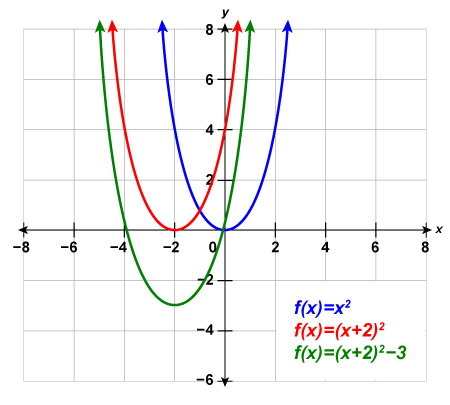
Example 4.7.5
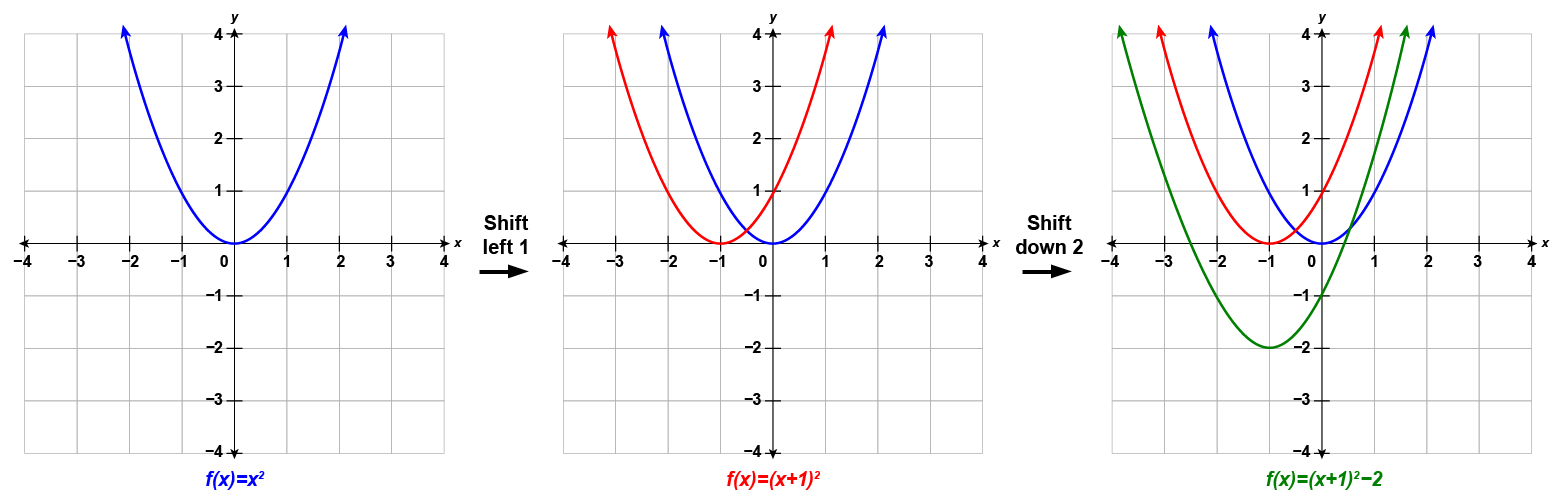
Graph [latex]f\left(x\right)={\left(x+1\right)}^{2}-2[/latex] using transformations.
Solution
Step 1: This function will involve two transformations and we need a plan.
Let’s first identify the constants [latex]h[/latex], [latex]k[/latex].
[latex]{\color{red}{f}}{{\color{red}{(}}{\color{red}{x}}{\color{red}{)}}{\color{red}{=}}{\color{red}{\left(x+1\right)}}^{\color{red}{2}}{\color{red}{-}}}{\color{red}{2}}[/latex]
[latex]\begin{array}{c}f\left(x\right)=\left(x-h\right)^2+k\\{\color{red}{f}}{\color{red}{\left(x\right)}}{\color{red}{=}}{\color{red}{\left(x-\left(-1\right)\right)}}^{\color{red}{2}}{\color{red}{+}}{\color{red}{\left(-2\right)}}\end{array}[/latex]
[latex]h=-1\text{, }k=-2[/latex]
Step 2: The [latex]h[/latex] constant gives us a horizontal shift and the [latex]k[/latex] gives us a vertical shift.
[latex]\begin{array}{ccccc}f(x)=x^2&\xrightarrow{}&f(x)=(x+1)^2&\xrightarrow{}&f(x)=(x+1)^2-2\\&h=-1&&k=-2&\\&\text{Shift left 1 unit}&&\text{Shift down 2 units}&\end{array}[/latex]
Step 3: We first draw the graph of [latex]f\left(x\right)={x}^{2}[/latex] on the grid.
To graph [latex]{\color{red}{f}}{\color{red}{\left(x\right)}}{\color{red}{=}}{\color{red}{\left(x+1\right)}}^{\color{red}{2}}[/latex], shift the graph [latex]{\color{blue}{f}}{\color{blue}{\left(x\right)}}{\color{blue}{=}}{\color{blue}{x}}^{\color{blue}{2}}[/latex] to the left [latex]1[/latex] unit.
To graph [latex]{\color{green}{f}}{{\color{green}{\left(x\right)}}{\color{green}{=}}{\color{green}{\left(x+1\right)}}^{\color{green}{2}}{\color{green}{-}}}{\color{green}{2}}[/latex], shift the graph [latex]{\color{red}{f}}{\color{red}{\left(x\right)}}{\color{red}{=}}{\color{red}{\left(x+1\right)}}^{\color{red}{2}}[/latex] down [latex]2[/latex] units.
Graph Quadratic Functions of the Form [latex]f(x)=ax^2[/latex]
So far we graphed the quadratic function [latex]f\left(x\right)={x}^{2}[/latex] and then saw the effect of including a constant [latex]h[/latex] or [latex]k[/latex] in the equation had on the resulting graph of the new function. We will now explore the effect of the coefficient [latex]a[/latex] on the resulting graph of the new function [latex]f\left(x\right)=a{x}^{2}[/latex].
Lets look at the quadratic functions [latex]{\color{blue}{f}}{\color{blue}{(}}{\color{blue}{x}}{\color{blue}{)}}{\color{blue}{=}}{\color{blue}{x}}^{\color{blue}{2}}[/latex], [latex]{\color{red}{g}}{\color{red}{(}}{\color{red}{x}}{\color{red}{)}}{\color{red}{=}}{\color{red}{2}}{\color{red}{x}}^{\color{red}{2}}{}[/latex] and [latex]{\color{green}{h}}{\color{green}{(}}{\color{green}{x}}{\color{green}{)}}{\color{green}{=}}{\color{green}{\frac12}}{\color{green}{x}}^{\color{green}{2}}[/latex].
| [latex]x[/latex] | [latex]{\color{blue}{\boldsymbol f}}{\color{blue}{\mathbf(}}{\color{blue}{\boldsymbol x}}{\color{blue}{\mathbf)}}{\color{blue}{\mathbf=}}{\color{blue}{\boldsymbol x}}^{\color{blue}{\mathbf2}}[/latex] | [latex]{\color{blue}{\mathbf(}}{{\color{blue}{\boldsymbol x}}{\color{blue}{\mathbf,}}{\color{blue}{\boldsymbol f}}{\color{blue}{\mathbf(}}{\color{blue}{\boldsymbol x}}{\color{blue}{\mathbf)}}}{\color{blue}{\mathbf)}}[/latex] | [latex]{\color{red}{\boldsymbol g}}{\color{red}{\mathbf(}}{\color{red}{\boldsymbol x}}{\color{red}{\mathbf)}}{\color{red}{\mathbf=}}{\color{red}{\mathbf2}}{\color{red}{\boldsymbol x}}^{\color{red}{\mathbf2}}{}[/latex] | [latex]{\color{red}{\mathbf(}}{{\color{red}{\boldsymbol x}}{\color{red}{\mathbf,}}{\color{red}{\boldsymbol g}}{\color{red}{\mathbf(}}{\color{red}{\boldsymbol x}}{\color{red}{\mathbf)}}}{\color{red}{\mathbf)}}{}[/latex] | [latex]{\color{green}{\boldsymbol h}}{\color{green}{\mathbf(}}{\color{green}{\boldsymbol x}}{\color{green}{\mathbf)}}{\color{green}{\mathbf=}}{\color{green}{\frac{\mathbf1}{\mathbf2}}}{\color{green}{\boldsymbol x}}^{\color{green}{\mathbf2}}[/latex] | [latex]{\color{green}{\mathbf(}}{{\color{green}{\boldsymbol x}}{\color{green}{\mathbf,}}{\color{green}{\boldsymbol h}}{\color{green}{\mathbf(}}{\color{green}{\boldsymbol x}}{\color{green}{\mathbf)}}}{\color{green}{\mathbf)}}[/latex] |
|---|---|---|---|---|---|---|
| [latex]-2[/latex] | [latex]4[/latex] | [latex](-2,4)[/latex] | [latex]4\times2[/latex] | [latex](-2,8)[/latex] | [latex]\frac12\times4[/latex] | [latex](-2,2)[/latex] |
| [latex]-1[/latex] | [latex]1[/latex] | [latex](-1,1)[/latex] | [latex]1\times2[/latex] | [latex](-1,2)[/latex] | [latex]\frac12\times1[/latex] | [latex](-1,\frac12)[/latex] |
| [latex]0[/latex] | [latex]0[/latex] | [latex](0,0)[/latex] | [latex]0\times2[/latex] | [latex](0,0)[/latex] | [latex]\frac12\times0[/latex] | [latex](0,0)[/latex] |
| [latex]1[/latex] | [latex]1[/latex] | [latex](1,1)[/latex] | [latex]1\times2[/latex] | [latex](1,2)[/latex] | [latex]\frac12\times1[/latex] | [latex](1,\frac12)[/latex] |
| [latex]2[/latex] | [latex]4[/latex] | [latex](2,4)[/latex] | [latex]4\times2[/latex] | [latex](2,8)[/latex] | [latex]\frac12\times4[/latex] | [latex](2,2)[/latex] |
If we graph these functions, we can see the effect of the constant [latex]a[/latex], assuming [latex]a>0[/latex].
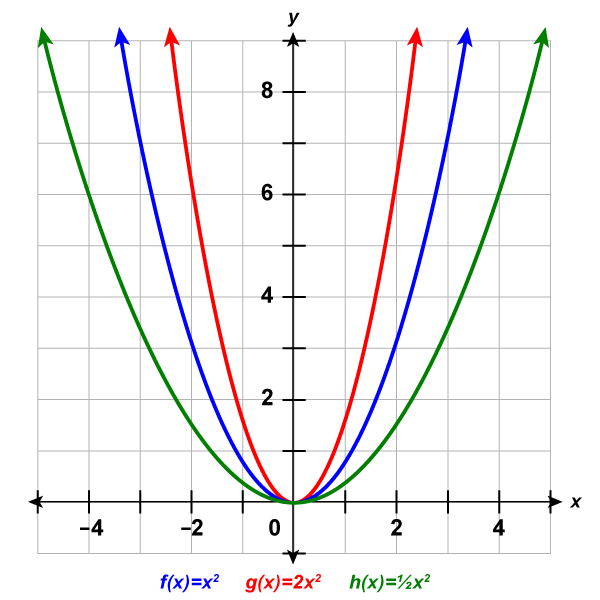
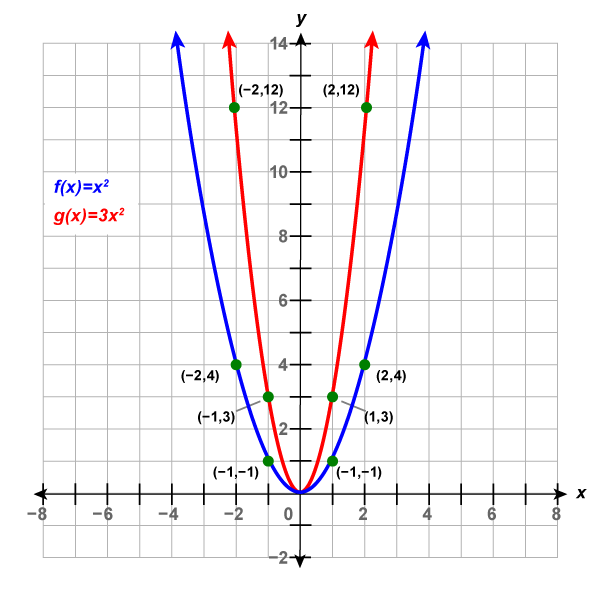
The graph of the function [latex]{\color{red}{g}}{\color{red}{(}}{\color{red}{x}}{\color{red}{)}}{\color{red}{=}}{\color{red}{2}}{\color{red}{x}}^{\color{red}{2}}[/latex] is "skinnier" than the graph of [latex]{\color{blue}{f}}{\color{blue}{(}}{\color{blue}{x}}{\color{blue}{)}}{\color{blue}{=}}{\color{blue}{x}}^{\color{blue}{2}}[/latex].
The graph of the function [latex]{\color{green}{h}}{\color{green}{(}}{\color{green}{x}}{\color{green}{)}}{\color{green}{=}}{\color{green}{\frac12}}{\color{green}{x}}^{\color{green}{2}}[/latex] is "wider" than the graph of [latex]{\color{blue}{f}}{\color{blue}{(}}{\color{blue}{x}}{\color{blue}{)}}{\color{blue}{=}}{\color{blue}{x}}^{\color{blue}{2}}[/latex].
To graph a function with constant [latex]a[/latex] it is easiest to choose a few points on [latex]f\left(x\right)={x}^{2}[/latex] and multiply the [latex]y[/latex]-values by [latex]a[/latex].
Graph of a Quadratic Function of the form [latex]f\left(x\right)=a{x}^{2}[/latex]
The coefficient [latex]a[/latex] in the function [latex]f\left(x\right)=a{x}^{2}[/latex] affects the graph of [latex]f\left(x\right)={x}^{2}[/latex] by stretching or compressing it.
- If [latex]0<|a|<1[/latex], the graph of [latex]f\left(x\right)=a{x}^{2}[/latex] will be “wider” than the graph of [latex]f\left(x\right)={x}^{2}[/latex].
- If [latex]|a|>1[/latex], the graph of [latex]f\left(x\right)=a{x}^{2}[/latex] will be “skinnier” than the graph of [latex]f\left(x\right)={x}^{2}[/latex].
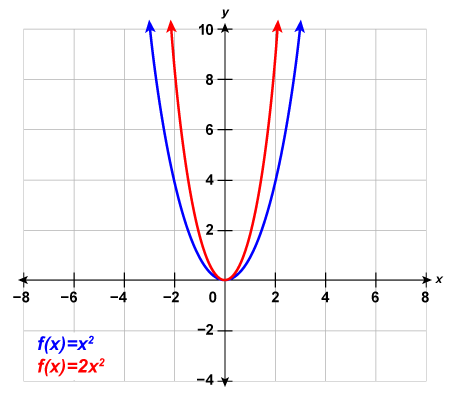
Example 4.7.6
Graph [latex]f\left(x\right)=3{x}^{2}[/latex].
Solution
Step 1: We will graph the functions [latex]f\left(x\right)={x}^{2}[/latex] and [latex]g\left(x\right)=3{x}^{2}[/latex] on the same grid.
We will choose a few points on [latex]f\left(x\right)={x}^{2}[/latex] and then multiply the [latex]y[/latex]-values by [latex]3[/latex] to get the points for [latex]g\left(x\right)=3{x}^{2}[/latex].
| [latex]{\color{blue}{\boldsymbol f}}{\color{blue}{\mathbf(}}{\color{blue}{\boldsymbol x}}{\color{blue}{\mathbf)}}{\color{blue}{\mathbf=}}{\color{blue}{\boldsymbol x}}^{\color{blue}{\mathbf2}}[/latex] | [latex]{\color{red}{\boldsymbol g}}{\color{red}{\mathbf(}}{\color{red}{\boldsymbol x}}{\color{red}{\mathbf)}}{\color{red}{\mathbf=}}{\color{red}{\mathbf3}}{\color{red}{\boldsymbol x}}^{\color{red}{\mathbf2}}[/latex] | ||
|---|---|---|---|
| [latex]x[/latex] | [latex]\mathbf{\color{blue}{\left({x,f\left(x\right)}\right)}}[/latex] | [latex]\mathbf{\color{red}{\left({x,g\left(x\right)}\right)}}[/latex] | |
| [latex]-2[/latex] | [latex](-2,4)[/latex] | [latex](-2,12)[/latex] | [latex]3\times4=12[/latex] |
| [latex]-1[/latex] | [latex](-1,1)[/latex] | [latex](-1,3)[/latex] | [latex]3\times1=3[/latex] |
| [latex]0[/latex] | [latex](0,0)[/latex] | [latex](0,0)[/latex] | [latex]3\times0=0[/latex] |
| [latex]1[/latex] | [latex](1,1)[/latex] | [latex](1,3)[/latex] | [latex]3\times1=3[/latex] |
| [latex]2[/latex] | [latex](2,4)[/latex] | [latex](2,12)[/latex] | [latex]3\times4=12[/latex] |
Graph Quadratic Functions Using Transformations
We have learned how the constants [latex]a[/latex], [latex]h[/latex], and [latex]k[/latex] in the functions, [latex]f\left(x\right)={x}^{2}+k[/latex], [latex]f\left(x\right)={\left(x-h\right)}^{2}[/latex], and [latex]f\left(x\right)=a{x}^{2}[/latex] affect their graphs. We can now put this together and graph quadratic functions [latex]f\left(x\right)=a{x}^{2}+bx+c[/latex] by first putting them into the form [latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex] by completing the square. This form is sometimes known as the vertex form or standard form.
We must be careful to both add and subtract the number to the SAME side of the function to complete the square. We cannot add the number to both sides as we did when we completed the square with quadratic equations.

When we complete the square in a function with a coefficient of [latex]x^2[/latex] that is not one, we have to factor that coefficient from just the [latex]x[/latex]-terms. We do not factor it from the constant term. It is often helpful to move the constant term a bit to the right to make it easier to focus only on the [latex]x[/latex]-terms.
Once we get the constant we want to complete the square, we must remember to multiply it by that coefficient before we then subtract it.
Example 4.7.7
Rewrite [latex]f\left(x\right)=-3{x}^{2}-6x-1[/latex] in the [latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex] form by completing the square.
Solution
Step 1: Separate the [latex]x[/latex]-terms from the constant.
[latex]f(x)=-3x^2-6x -1[/latex]
Step 2: Factor the coefficient of [latex]{x}^{2}[/latex], [latex]-3[/latex].
[latex]f(x)=-3(x^2+2x) -1[/latex]
Step 3: Prepare to complete the square.
[latex]f(x)=-3(x^2+2x ) -1[/latex]
Step 4: Take half of [latex]2[/latex] and then square it to complete the square.
[latex]{\left(\frac{1}{2}·2\right)}^{2}=1[/latex]
Step 5: The constant [latex]1[/latex] completes the square in the parentheses, but the parentheses is multiplied by [latex]-3[/latex].
So we are really adding [latex]-3[/latex] We must then add [latex]3[/latex] to not change the value of the function.
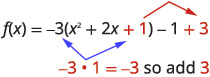
Step 6: Rewrite the trinomial as a square and subtract the constants.
[latex]f(x)=-3(x+1)+2[/latex]
Step 7: The function is now in the [latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex] form.
[latex]{\color{red}{f}}{{\color{red}{(}}{\color{red}{x}}{\color{red}{)}}{\color{red}{=}}{\color{red}{a}}{\color{red}{{(x-h)}}}^{\color{red}{2}}{\color{red}{+}}}{\color{red}{k}}[/latex]
[latex]f(x)=-3{(x+1)}^2+2[/latex]
Try It
16) Rewrite [latex]f\left(x\right)=-4{x}^{2}-8x+1[/latex] in the [latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex] form by completing the square.
Solution
[latex]f\left(x\right)=-4{\left(x+1\right)}^{2}+5[/latex]
Try It
17) Rewrite [latex]f\left(x\right)=2{x}^{2}-8x+3[/latex] in the [latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex] form by completing the square.
Solution
[latex]f\left(x\right)=2{\left(x-2\right)}^{2}-5[/latex]
Once we put the function into the [latex]f\left(x\right)={\left(x-h\right)}^{2}+k[/latex] form, we can then use the transformations as we did in the last few problems. The next example will show us how to do this.
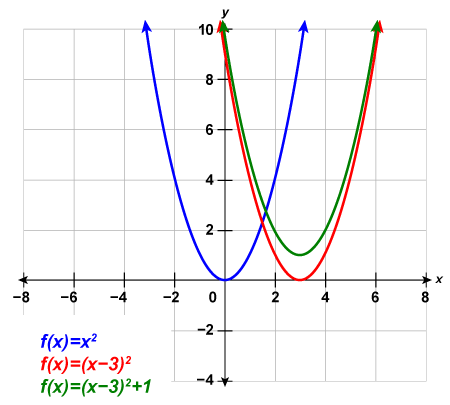
Example 4.7.8
Graph [latex]f\left(x\right)={x}^{2}+6x+5[/latex] by using transformations.
Solution
Step 1: Rewrite the function in [latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex] vertex form by completing the square.
Separate the [latex]x[/latex] terms from the constant.
[latex]x^2+6x\;\;\;\;+5[/latex]
Take half of [latex]6[/latex] and then square it to complete the square.
[latex]{\left(\frac{1}{2}\times6\right)}^{2}=9[/latex]
We both add [latex]9[/latex] and subtract [latex]9[/latex] to not change the value of the function.
[latex]{f(x)=x^2+6x}{\color{red}{\;+9}}{+5}{\color{red}{\;-9}}[/latex]
Rewrite the trinomial as a square and subtract the constants.
[latex]f(x)=(x+3)^2-4[/latex]
The function is now in the [latex]f\left(x\right)={\left(x-h\right)}^{2}+k[/latex] form.
[latex]\overset{\color{red}{f(x)=(x-h)^2+k}}{f(x)=(x+3)^2-4}[/latex]
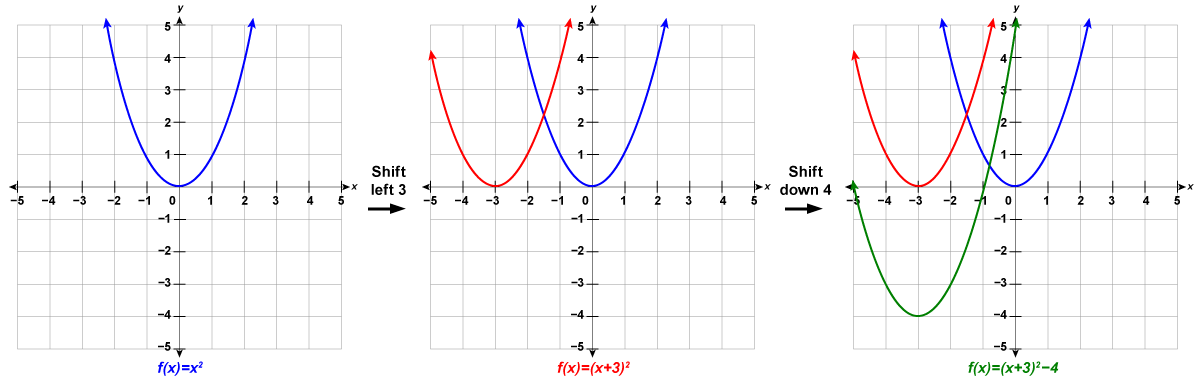
Step 2: Graph the function using transformations.
Looking at the [latex]h[/latex], [latex]k[/latex] values, we see the graph will take the graph of [latex]f\left(x\right)={x}^{2}[/latex] and shift it to the left [latex]3[/latex] units and down [latex]4[/latex] units.
[latex]\begin{array}{c}f(x)=x^2&\xrightarrow{}&f(x)=(x+3)^2&\xrightarrow{}&f(x)=(x+3)^2-4\\&h=-3&&k=-4&\\&\text{Shift left 3 units}&&\text{Shift down 4 units}&\end{array}[/latex]
We first draw the graph of [latex]f\left(x\right)={x}^{2}[/latex] on the grid.
To graph [latex]{\color{red}{ f(x)=(x+3)^2}}[/latex], shift the graph [latex]{\color{Blue} f(x)=x^2}[/latex] to the left [latex]3[/latex] units.
To graph [latex]{\color{DarkGreen}{f(x)=(x+3)^2-4}}[/latex], shift the graph [latex]{\color{Red}{f(x)=(x+3)^2}}[/latex] down [latex]4[/latex] units.
Try It
Try It
We list the steps to take to graph a quadratic function using transformations here.
HOW TO
Graph a quadratic function using transformations.
- Rewrite the function in [latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex] form by completing the square.
- Graph the function using transformations.
Example 4.7.9
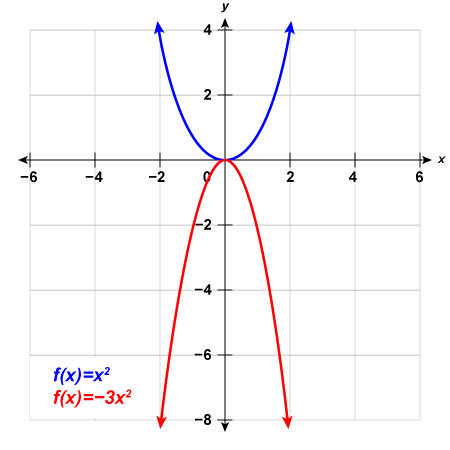
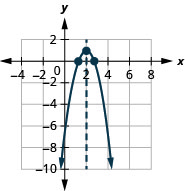
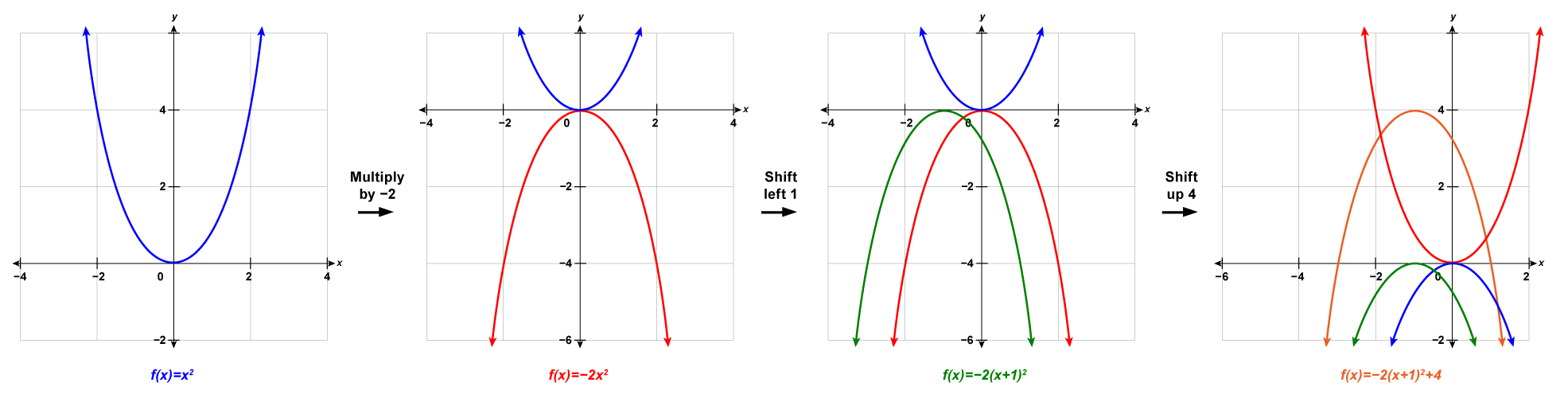
Graph [latex]f\left(x\right)=-2{x}^{2}-4x+2[/latex] by using transformations.
Solution
Step 1: Rewrite the function in [latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex] vertex form by completing the square.
Separate the [latex]x[/latex] terms from the constant.
[latex]f(x)=-2x^2-4x\;\;\;\;+2[/latex]
We need the coefficient of [latex]{x}^{2}[/latex] to be one. We factor [latex]-2[/latex] from the [latex]x[/latex]-terms.
[latex]f(x)=-2(x^2+2x)+2[/latex]
Take half of [latex]2[/latex] and then square it to complete the square.
[latex]{\left(\frac{1}{2}\times2\right)}^{2}=1[/latex]
We add [latex]1[/latex] to complete the square in the parentheses, but the parentheses is multiplied by [latex]-2[/latex]. Se we are really adding [latex]-2[/latex]. To not change the value of the function we add [latex]2[/latex].
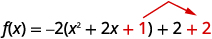
The function is now in the [latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex] form.
[latex]{\color{red}{f}}{{\color{red}{(}}{\color{red}{x}}{\color{red}{)}}{\color{red}{=}}{\color{red}{a}}{{\color{red}{(}}{\color{red}{x}}{\color{red}{-}}{\color{red}{h}}{\color{red}{)}}}^{\color{red}{2}}{\color{red}{+}}}{\color{red}{k}}[/latex]
[latex]f(x)=-2{(x+1)}^2+4[/latex]
Step 2: Graph the function using transformations.
[latex]\begin{array}{ccccccc}f(x)=x^2&\xrightarrow{}&f(x)=-2x^2&\xrightarrow{}&f(x)=-2(x+1)^2&\xrightarrow{}&f(x)=-2(x+1)^2+4\\&a=-2&&h=-1&&k=4&\\&\begin{array}{c}\text{Multiply}\\\text{y-values}\\\text{by -2}\end{array}&&\begin{array}{c}\text{Shift left}\\\text{1 unit}\end{array}&&\begin{array}{c}\text{Shift up}\\\text{4 units}\end{array}&\end{array}[/latex]
We first draw the graph of [latex]f\left(x\right)={x}^{2}[/latex] on the grid.
To graph [latex]{\color{Red} f(x)=-2x^2}[/latex], multiply the [latex]y[/latex]-values in parabola of [latex]{\color{Blue} f(x)=x^2}[/latex] by [latex]-2[/latex].
To graph [latex]{\color{DarkGreen} f(x)=-2(x+1)^2}[/latex], shift the graph [latex]{\color{Red} f(x)=-2x^2}[/latex] to the left [latex]1[/latex] unit.
To graph [latex]{\color{Orange} f(x)=-2(x+1)^2+4}[/latex], shift the graph of [latex]{\color{DarkGreen} f(x)=-2(x+1)^2}[/latex] up [latex]4[/latex] units.
Try It
Try It
Now that we have completed the square to put a quadratic function into [latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex] form, we can also use this technique to graph the function using its properties as in the previous section.
If we look back at the last few examples, we see that the vertex is related to the constants [latex]h[/latex] and [latex]k[/latex].
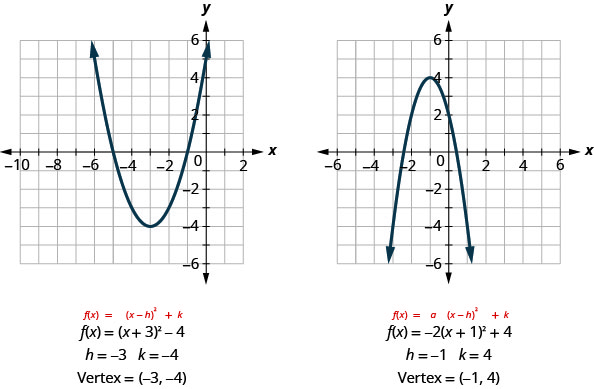
In each case, the vertex is ([latex]h[/latex], [latex]k[/latex]). Also the axis of symmetry is the line [latex]x=h[/latex].
We rewrite our steps for graphing a quadratic function using properties for when the function is in [latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex] form.
HOW TO
Graph a quadratic function in the form [latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex] using properties.
- Rewrite the function in [latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex] form.
- Determine whether the parabola opens upward, [latex]a>0[/latex], or downward, [latex]a<0[/latex].
- Find the axis of symmetry, [latex]x=h[/latex].
- Find the vertex, ([latex]h[/latex], [latex]k[/latex]).
- Find the [latex]y[/latex]-intercept. Find the point symmetric to the [latex]y[/latex]-intercept across the axis of symmetry.
- Find the [latex]x[/latex]-intercepts.
- Graph the parabola.
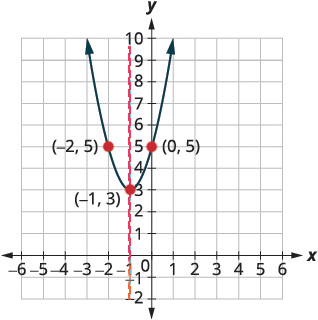
Example 4.7.10
a. Rewrite [latex]f\left(x\right)=2{x}^{2}+4x+5[/latex] in [latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex] form and
b. graph the function using properties.
Solution
a.
Step 1: Rewrite the function in [latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex] form by completing the square.
[latex]f\left(x\right)=2{x}^{2}+4x+5[/latex]
Step 2: Identify the constants [latex]a,h,k[/latex].
[latex]\begin{array}{rcl}f\left(x\right)&=&2\left({x}^{2}+2x\right)+5\\f\left(x\right)&=&2\left({x}^{2}+2x+1\right)+5-2\\f\left(x\right)&=&2{\left(x+1\right)}^{2}+3\end{array}[/latex]
[latex]\begin{array}{c}a=2&&h=-1&&k=3\end{array}[/latex]
Step 3: Since [latex]a=2[/latex], the parabola opens upward.

Step 4: The axis of symmetry is [latex]x=h[/latex].
The axis of symmetry is [latex]x=-1[/latex].
Step 5: The vertex is [latex]\left(h,k\right)[/latex].
The vertex is [latex]\left(-1,3\right)[/latex].
Step 6: Find the [latex]y[/latex]-intercept by finding [latex]f\left(0\right)[/latex].
[latex]f\left(0\right)=2\cdot {0}^{2}+4\cdot 0+5[/latex]
Step 7: Find the point symmetric to [latex]\left(0,5\right)[/latex] across the axis of symmetry.
[latex](-2,5)[/latex]
Step 8: Find the [latex]x[/latex]-intercepts.
The discriminant is negative, so there are no [latex]x[/latex]-intercepts.
b.
Step 1: Graph the parabola.
Try It
Try It
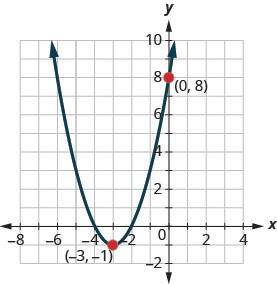
Find a Quadratic Function from its Graph
So far we have started with a function and then found its graph.
Now we are going to reverse the process. Starting with the graph, we will find the function.
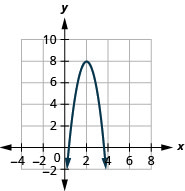
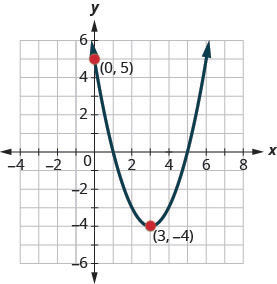
Example 4.7.11
Determine the quadratic function whose graph is shown.
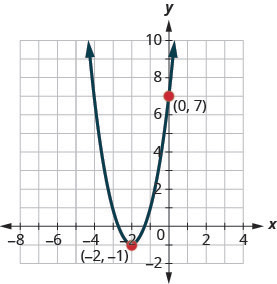
Solution
Step 1: Since it is quadratic, we start with the [latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex] form.
The vertex, [latex]\left(h,k\right)[/latex] is [latex]\left(-2,-1\right)[/latex], so [latex]h=-2[/latex] and [latex]k=-1[/latex].
[latex]f\left(x\right)=a{\left(x-\left(-2\right)\right)}^{2}-1[/latex]
Step 2: To find [latex]a[/latex], we use the [latex]y[/latex]-intercept, [latex](0,7)[/latex].
So [latex]f(0)=7[/latex].
[latex]7=a(x-(-2))^2-1[/latex]
Step 3: Solve for [latex]a[/latex].
[latex]\begin{array}{rcl}7&=&a(0+2)^2-1\\7&=&4a-1\\8&=&4a\\2&=&a\end{array}[/latex]
Step 4: Write the function.
[latex]f(x)=a(x-h)^2+k[/latex]
Step 5: Substitute in [latex]h=-2[/latex], [latex]k=-1[/latex], and [latex]a=2[/latex].
[latex]f(x)=2(x+2)^2-1[/latex]
Try It
Try It
Access these online resources for additional instruction and practice with graphing quadratic functions using transformations.
Key Concepts
- Graph a Quadratic Function of the form [latex]f\left(x\right)={x}^{2}+k[/latex] Using a Vertical Shift
- The graph of [latex]f\left(x\right)={x}^{2}+k[/latex] shifts the graph of [latex]f\left(x\right)={x}^{2}[/latex] vertically [latex]k[/latex] units.
- If [latex]k>0[/latex], shift the parabola vertically up [latex]k[/latex] units.
- If [latex]k<0[/latex], shift the parabola vertically down [latex]|k|[/latex] units.
- The graph of [latex]f\left(x\right)={x}^{2}+k[/latex] shifts the graph of [latex]f\left(x\right)={x}^{2}[/latex] vertically [latex]k[/latex] units.
- Graph a Quadratic Function of the form [latex]f\left(x\right)={\left(x-h\right)}^{2}[/latex] Using a Horizontal Shift
- The graph of [latex]f\left(x\right)={\left(x-h\right)}^{2}[/latex] shifts the graph of [latex]f\left(x\right)={x}^{2}[/latex] horizontally [latex]h[/latex] units.
- If [latex]h>0[/latex], shift the parabola horizontally left [latex]h[/latex] units.
- If [latex]h<0[/latex], shift the parabola horizontally right [latex]|h|[/latex] units.
- The graph of [latex]f\left(x\right)={\left(x-h\right)}^{2}[/latex] shifts the graph of [latex]f\left(x\right)={x}^{2}[/latex] horizontally [latex]h[/latex] units.
- Graph of a Quadratic Function of the form [latex]f\left(x\right)=a{x}^{2}[/latex]
- The coefficient [latex]a[/latex] in the function [latex]f\left(x\right)=a{x}^{2}[/latex] affects the graph of [latex]f\left(x\right)={x}^{2}[/latex] by stretching or compressing it.
If [latex]0<|a|<1[/latex], then the graph of [latex]f\left(x\right)=a{x}^{2}[/latex] will be “wider” than the graph of [latex]f\left(x\right)={x}^{2}[/latex].
If [latex]|a|>1[/latex], then the graph of [latex]f\left(x\right)=a{x}^{2}[/latex] will be “skinnier” than the graph of [latex]f\left(x\right)={x}^{2}[/latex].
- The coefficient [latex]a[/latex] in the function [latex]f\left(x\right)=a{x}^{2}[/latex] affects the graph of [latex]f\left(x\right)={x}^{2}[/latex] by stretching or compressing it.
- How to graph a quadratic function using transformations
- Rewrite the function in [latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex] form by completing the square.
- Graph the function using transformations.
- Graph a quadratic function in the vertex form [latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex] using properties
- Rewrite the function in [latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex] form.
- Determine whether the parabola opens upward, [latex]a>0[/latex], or downward, [latex]a<0[/latex].
- Find the axis of symmetry, [latex]x=h[/latex].
- Find the vertex, ([latex]h[/latex], [latex]k[/latex]).
- Find the [latex]y[/latex]-intercept. Find the point symmetric to the [latex]y[/latex]-intercept across the axis of symmetry.
- Find the [latex]x[/latex]-intercepts, if possible.
- Graph the parabola.
Self Check
a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
b) After looking at the checklist, do you think you are well-prepared for the next section? Why or why not?