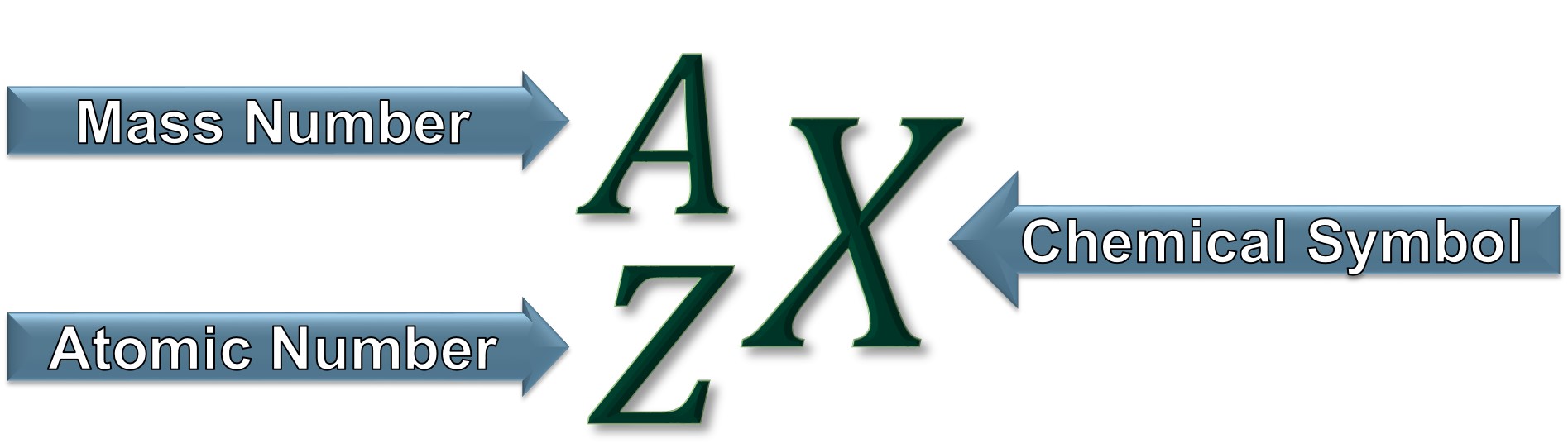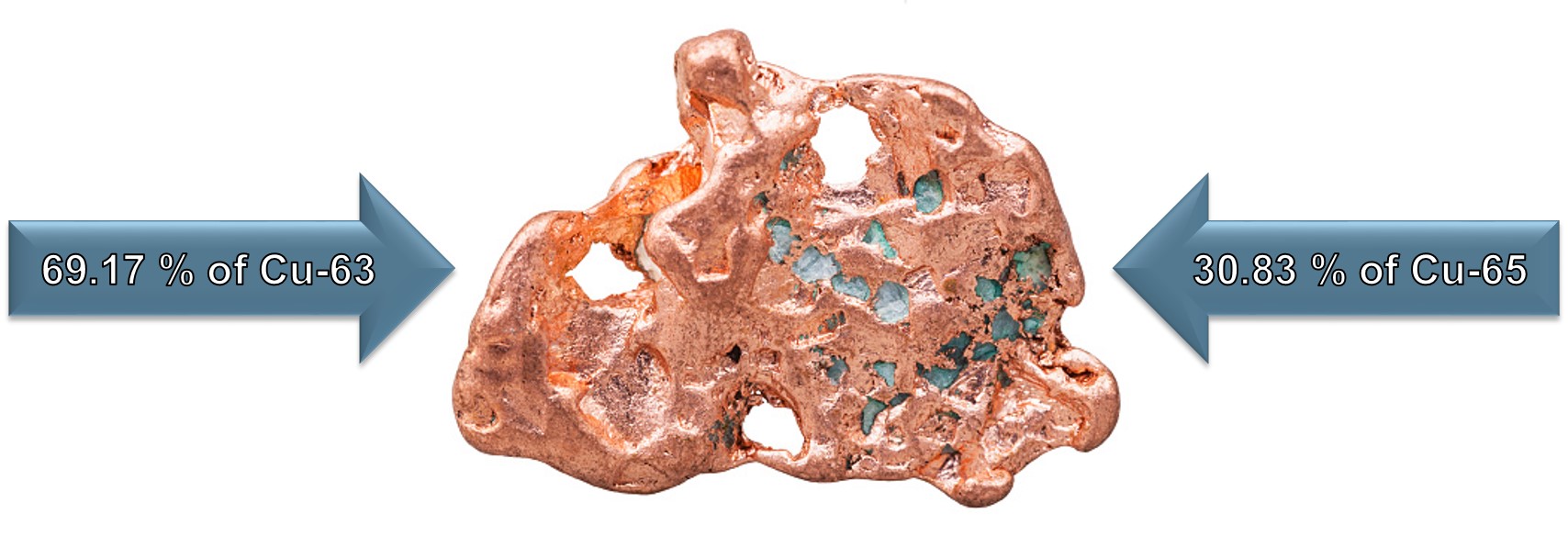Modern Atomic Theory

Andrew Vreugdenhil; Kelly Wright

5 Modern Atomic Theory

The Atom


Nucleus	Neutron	Proton
The small dense core of an atom consisting of neutrons and protons. Neutrons and protons have approximately the same mass.	A neutral particle located in the nucleus of an atom.	A positively charged particle located in the nucleus of an atom.

Electron		Charge
A negatively charged particle located in the volume of space surrounding the nucleus of an atom.		Electrons and protons have charge that is equal and opposite, because of this we can say the relative charge in atomic units is one.

A neutral atom has the same number of protons as electrons.

Physical Properties of Sub-atomic Particles

Particle

Charge (Coulombs)

Mass (kilograms)

Relative Charge

Mass (unified atomic mass units)

Proton

$+1.6 \times 10^{-19} C$

$1.673 \times 10^{-27} kg$

$+1$

$1.0073 u$

Neutron

No Charge

$1.675 \times 10^{-27} kg$

$0$

$1.0087 u$

Electron

$-1.6 \times 10^{-19} C$

$9.109 \times 10^{-31} kg$

$-1$

$5.4858 \times 10^{-4} u$

Unified atomic mass units (u):

$1/12$ the mass of a carbon atom containing six protons and six neutrons.

Using this measurement, the mass of a proton and neutron is approximately $1 u$ .

The masses of all elements are defined using unified atomic mass units.

$1u = 1.661 \times 10^{-27}kg = \frac{1}{12}$ the mass of a carbon atom.

Atom Terminology

Z = number of protons = atomic number

A = number of protons + number of neutrons = mass number

Element	Chemical Symbol (X)	Atomic Number (Z)	Mass Number (A)
One or more atoms of the same type.	A one or two letter abbreviation assigned to each element.	The number of protons in the nucleus of an atom. The type of atom/element is determined by the number of protons.	The sum of the number of neutrons and protons in the nucleus of an atom.

The number of protons defines the type of atom or element!

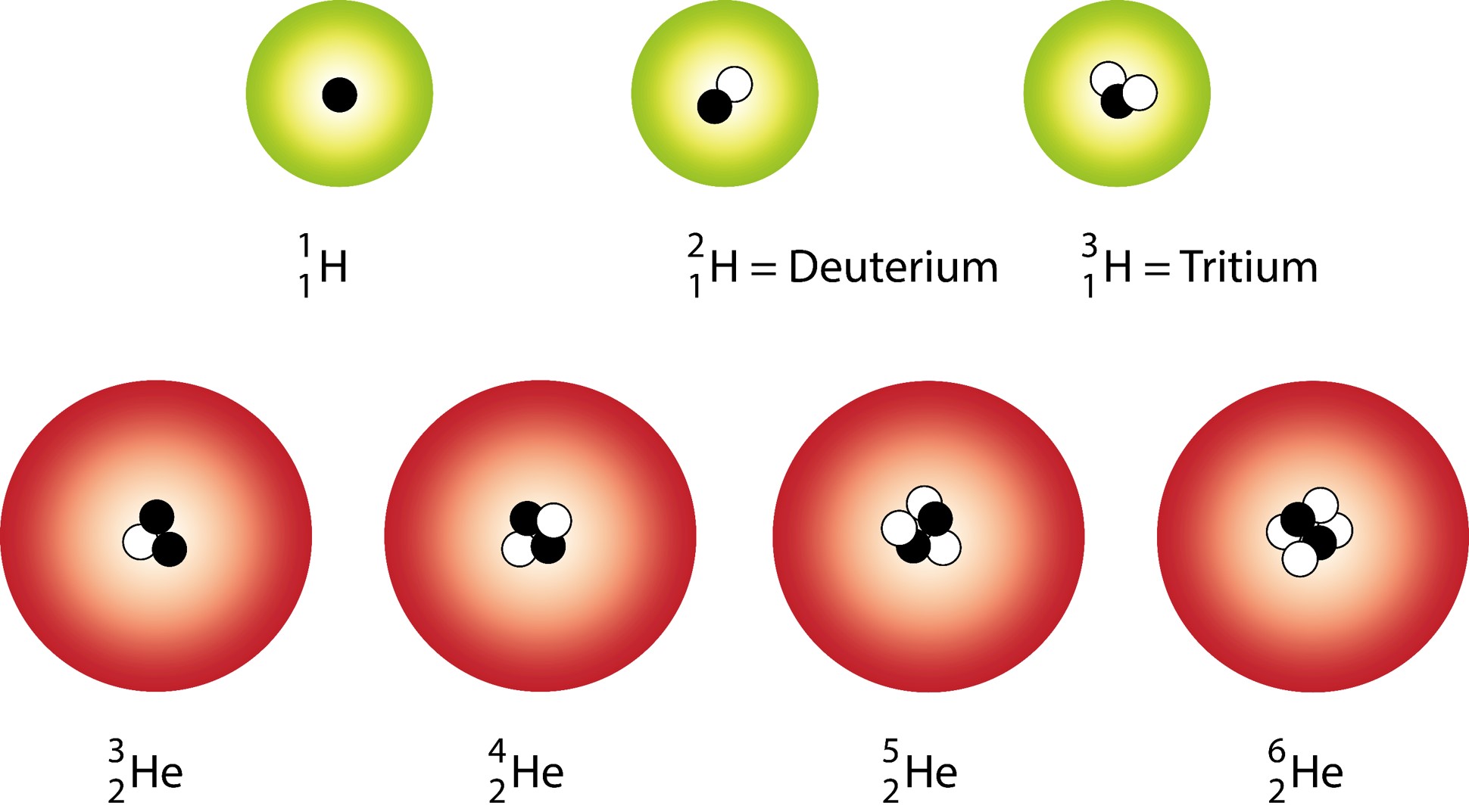
Isotopes

Isotopes are atoms of the same type that have the same number of protons and varying numbers of neutrons.

We know:

Isotopes:

The number of protons determines the type of atom or element.

Neutrons and protons comprise the nucleus of an atom and have the same approximate mass.

The number of protons determines the type of atom or element.

Isotopes of elements are distinguished by the mass number (A).

Isotopes Example:

Atoms of an element that have a different number of neutrons.

28-14=14 neutrons

29-14=15 neutrons

30-14=16 neutrons

Isotope Notation

Including the atomic number is redundant when representing isotopes. It is common to use the following notation: X-A.
For example: Si-28, Si-29, Si-30

Atomic Mass

We know:

Atomic Mass:

Isotopes are atoms of the same type that have a different number of neutrons.

The mass of an atom is dictated by the mass of protons and neutrons because the mass of an electron is negligible in comparison.

Is the weighted average of isotopic masses based on the natural abundance of each isotope.

The natural abundance is the relative amount of each isotope found in a natural sample of any element. Natural abundance is relatively constant and unique for each element.

The atomic mass of an element as seen on the periodic table is a weighted average of isotopic masses of that element.

Atomic Mass Example:

This Copper (Cu) sample will contain approximately 30.83 % of Cu-65 and 69.17 % of Cu-63

Atomic Mass Calculations:

Atomic mass for an element can be calculated with the following formula:

$\sum_{n} (\text{fraction of isotope } n) \times (\text{mass of isotope } n)$

In simple terms this formula is telling us that atomic mass can be calculated by:

1) Multiplying each isotopic mass of an element by its relative abundance.

2) Adding the resulting masses of the isotopes together.

An atomic mass calculation is included in the example section!

The Mole

A measurement similar to a pair, dozen or score. A pair is 2 objects, a dozen is 12 objects and a score is 20 objects.

$1 \text{mole} = 6.022 \times 10^{23}$ objects = Avogadro’s number

Crowd of fans	Great Wall of China	Sahara
One mole of people is the Earth’s population multiplied by $9\times 10^{23}$	One mole of bricks is equivalent to $2\times 10^{14}$ Great Walls of China.	One mole of sand is the entire Sahara Desert!

Defining the Mole:

The mole is defined using the C-12 isotope.

One mole = number of atoms in exactly 12 g C-12.

12 g of C-12 = 1 mole of C-12 atoms = exactly $6.02 \times 10^{23}$ C-12 atoms

The mass of one mole of C-12 atoms is 12 g

1 mole of carbon (C) = $6.02 \times 10^{23}$ atoms

Molar Mass:

Using C-12 as a standard for the mole gives a relationship between mass, number of atoms, and unified atomic mass units.

The mole can be used to count atoms based on their mass.

The molar mass of an element is the mass of one mole of each element.


1 mole of carbon (C) $6.02 \times 10^{23}$ atoms	1 mole of sulfur (S) $6.02 \times 10^{23}$ atoms	1 mole of gold (Au) $6.02 \times 10^{23}$ atoms

Molar Mass of an Element:

The molar mass of an element is the mass of one mole of each element.

Molar mass the mass of the x atoms of each element.

Molar mass is numerically equivalent to an element’s mass in unified atomic mass units .
Molar Mass $\frac{g}{mol}$ $\frac{g}{mol}$ is numerically equivalent to atomic mass $u$

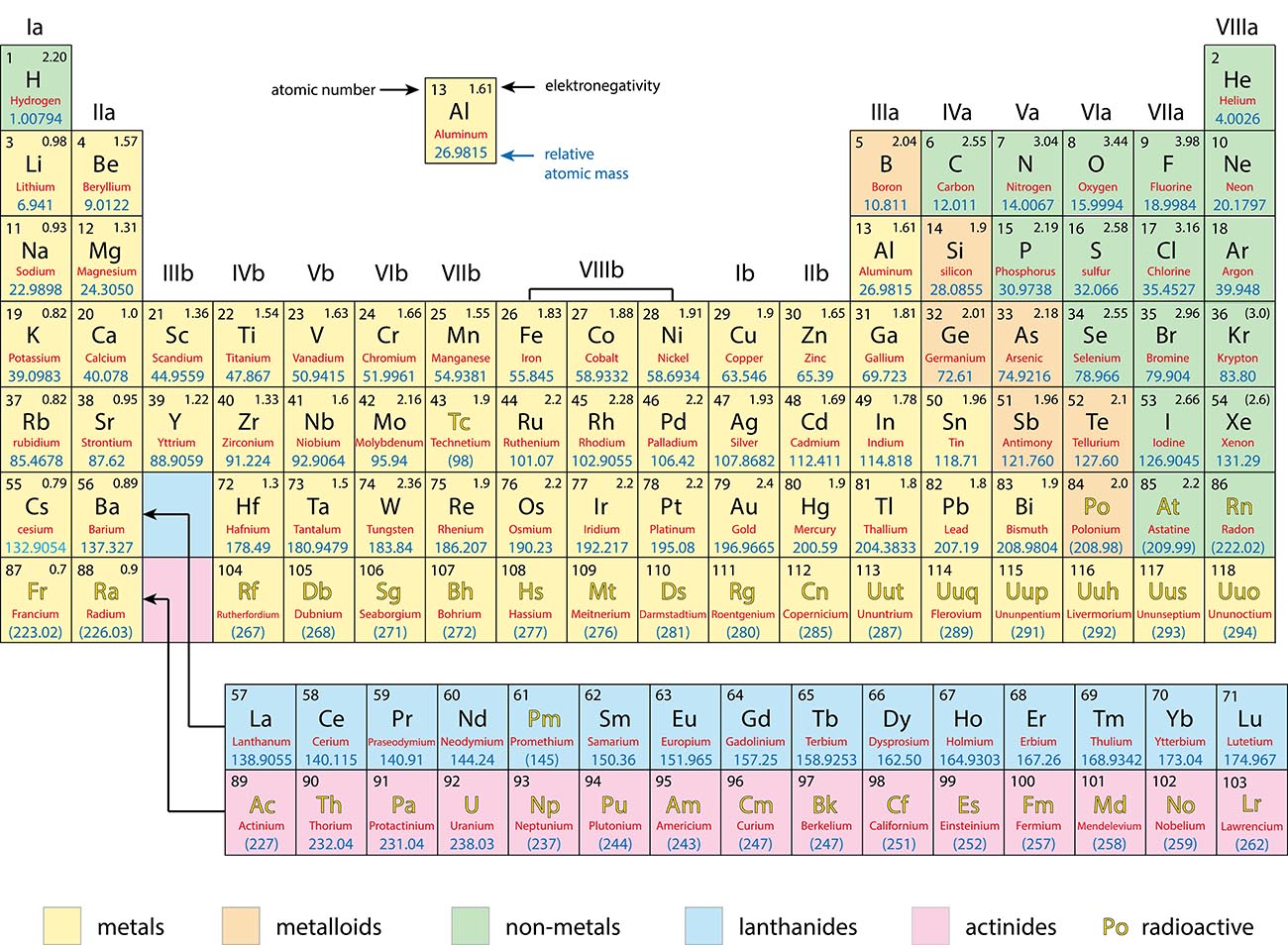
The Periodic Table of Elements

Metals, Non-Metals and Metalloids

Periodic Trends

Metals:

Non-Metals:

Metalloids:

Generally good conductors of heat and electricity

Tend to lose electrons in a chemical reaction

Generally poor conductors of heat and electricity

Tend to gain electrons in a chemical reaction

Have properties of both metals and non-metals.

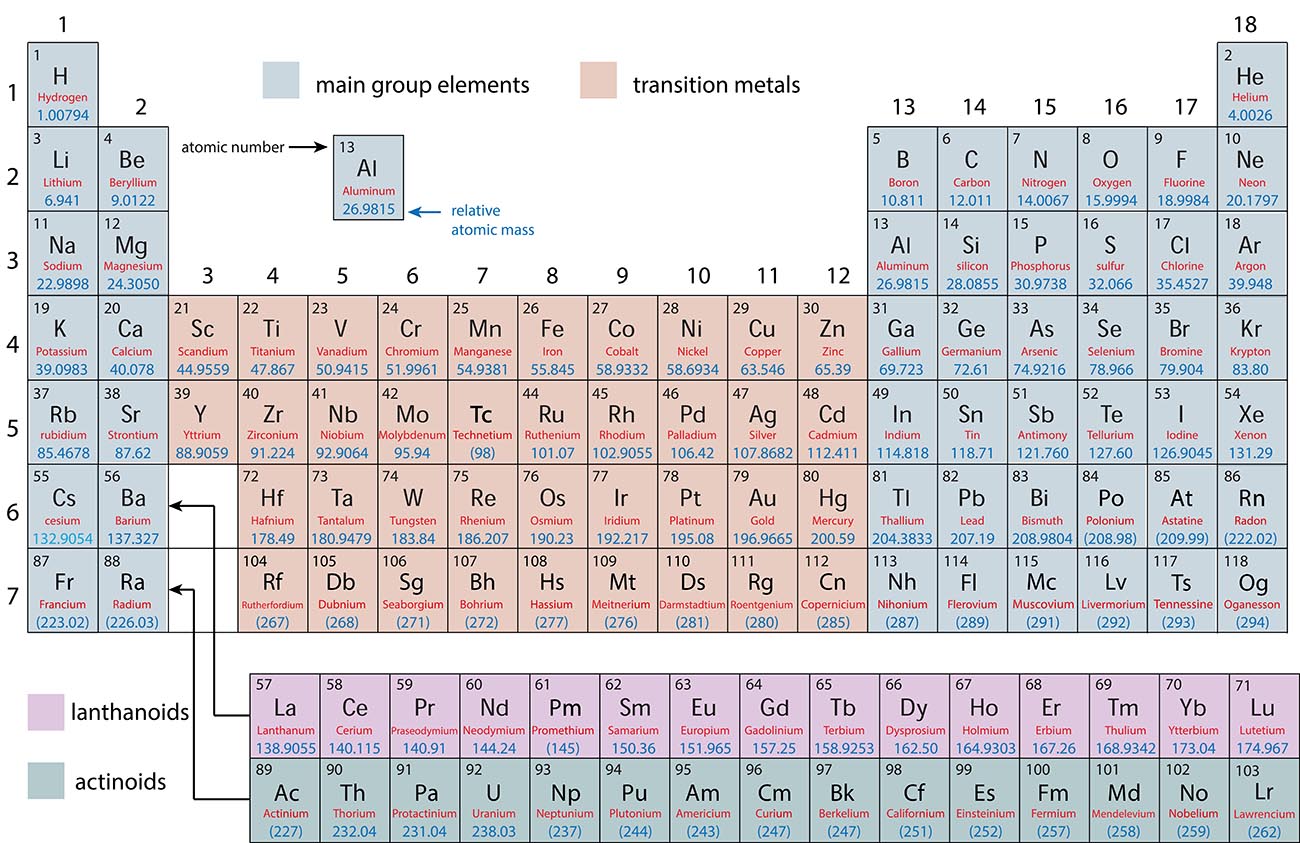
Main Group Elements and Transition Metals

Periodic Trends

Main Group:	Transition Metals:	Lanthanoids and Actinoids:
Elements that have predictable properties	Elements that have unpredictable properties.	Elements that are placed separately for a more compact periodic table. They have similar properties to the elements lanthanum and actinium.

Groups and Periods of the Periodic Table

Periodic Trends

Each column in the periodic table is called a group and numbered 1-18

Each row in the periodic table is called a row and numbered 1-7

The elements in a group have similar properties.

For example: The noble gases in group 18 are all relatively unreactive.

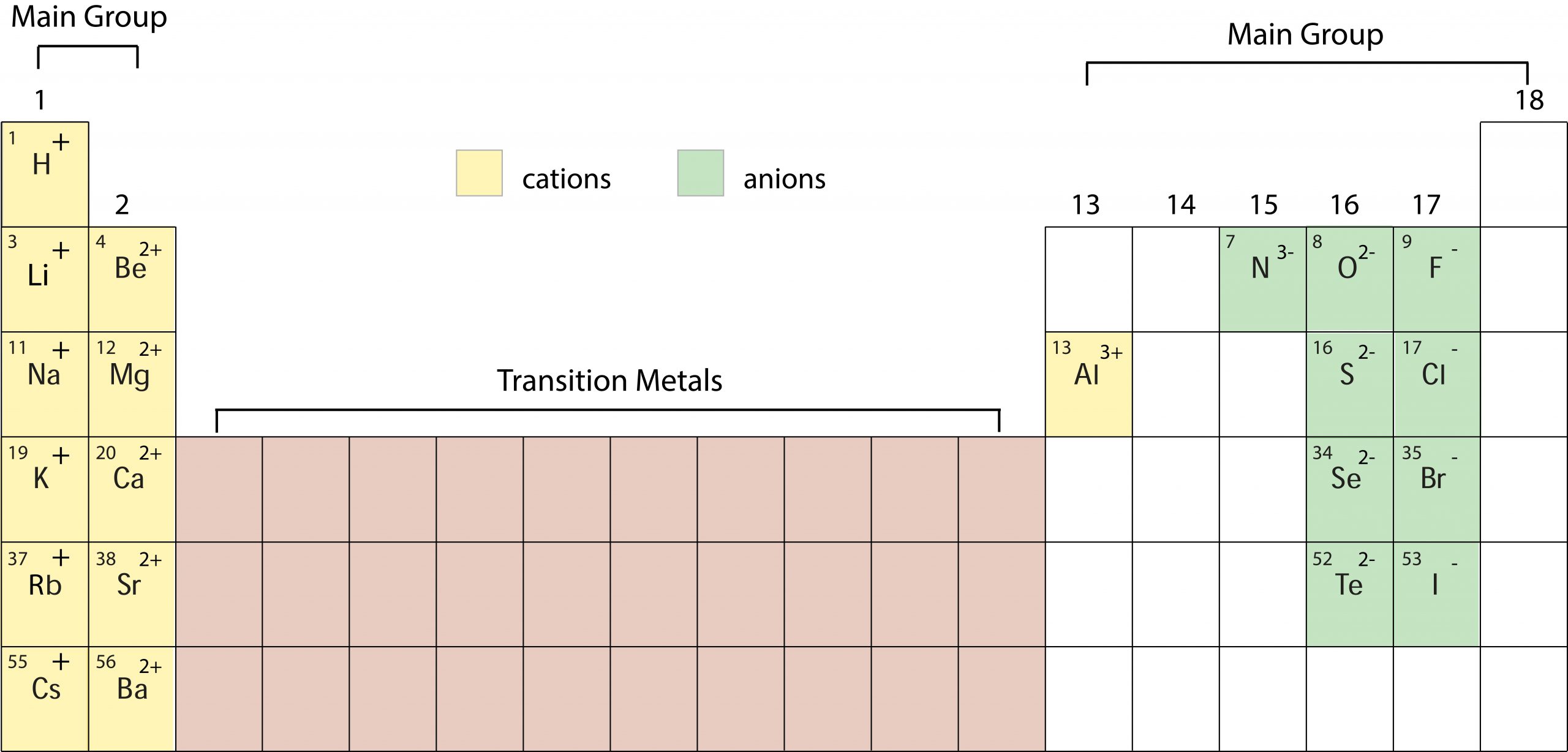
Ions

Common Main Group Ions:

We know:

Ions:

Ions and Groups:

The number of protons determines the type of atom or element.

Neutrons and protons comprise the nucleus of an atom, and have the same approximate mass.

One or more atoms that has gained or lost an electron(s).

Ions are charged particles.

The periodic table can help predict which ions will form.

A main group non-metal will generally gain electrons.

A main group metal will generally lose electrons.

Ions are charged particles that have gained or lost an electron(s).

Cation (+):

Anion (-):

Ion Notation:

One or more atoms that has lost an electron(s).

A main group METAL will LOSE electrons to form a CATION with the same number of electrons as the nearest noble gas.

One or more atoms that has gained an electron(s).

A main group NONMETAL will GAIN electrons to form an ANION with the same number of electrons as the nearest noble gas.

Ions are represented as the chemical symbol of the ion with the charge of the ion noted as a superscript to the right.

$X^{\text{charge}}$

Lithium Ion = $Li^{+}$
Oxygen Ion = $O^{2-}$

Examples

The following examples will walk you through solving a problem.

Example Problem 1

Calculate the average atomic mass of silicon given the information in the table.

Isotope	Percent Natural Abundance (%)	Mass (u)
Si-28	92.2	27.9769
Si-29	4.7	28.9764
Si-30	3.1	29.9738

Example Problem 2

These gold earrings have a mass of 1.00 g. Calculate the moles of gold in the earrings, how many gold atoms do the earrings contain? Assume the earrings are pure gold.

Problem Set

Below are two documents. One is practice problems, the second is the same problems with solutions.
They can be downloaded and changed to suit your needs.

Problem Set

Problem Set Solutions

Quiz

Atomic Structure

Video Transcript

Atom Models


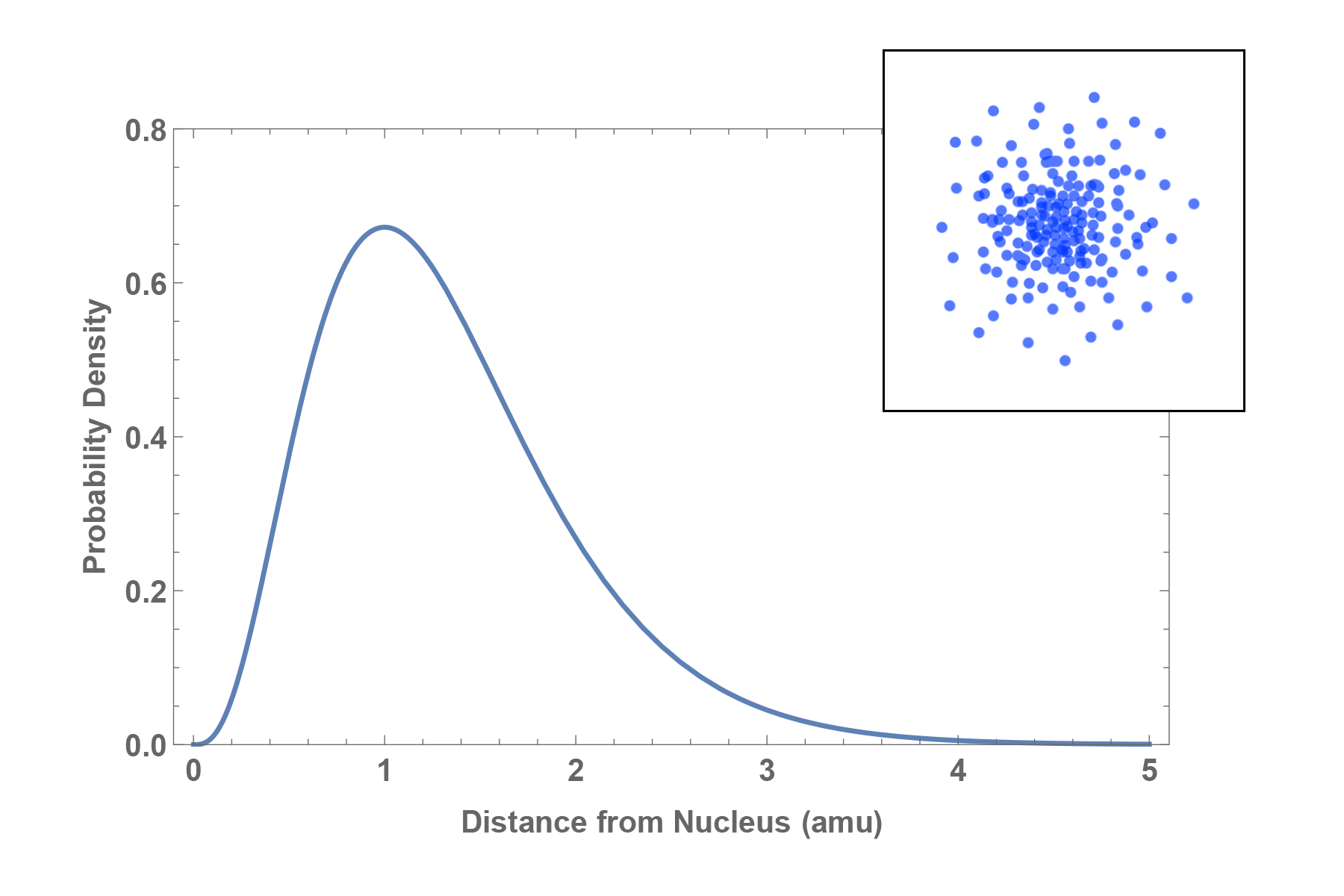
Bohr Model of an Atom	Quantum Mechanical Model of an Atom	Schrodinger – Quantum Mechanical Models
An electron’s position described as a trajectory.	An electron’s position described as a probability distribution.	Quantum Mechanical Model of an Atom. An electron’s position described as a probability distribution.

Orbital:

The likely position of an electron in an atom described by a probability distribution map.

Quantum Numbers = Electron’s “Address”

Quantum Numbers

Principal Quantum Number (n)

Angular Momentum Quantum Number (l)

Magnetic Quantum Number $(m_l)$

Orbital’s size and energy level of an electron.

A whole number 1,2,3,4…..

n increases with an electron’s energy and distance from the nucleus.

Each level is called a shell.

The shape of an orbital.

0,1,2,3,…,n-1

Each value for l is a subshell

Each number value of l is assigned a letter s,p,d,f,g….

Orientation of orbital in 3D space.

Value= integer values from –l…l.

There are 2(l)+1 values of $m_l$ for each value of l.

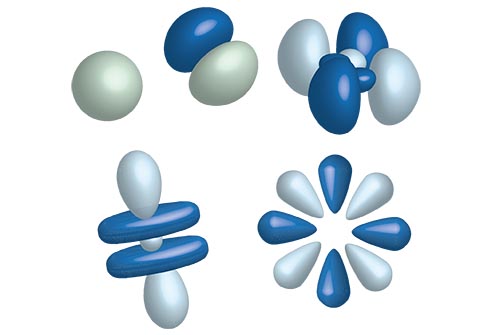
Orbital Shapes

Orbital Shapes = Angular Momentum Number (l)

Values of (l) angular momentum
Number	Letter
0	s
1	p
2	d
3	f
4	g

Letter values continue according to the alphabet after f, with the exception of J.

s,p,d,f,g,h,i,k,….. Sober Physicists Don’t Find Giraffes Hiding In Kitchens

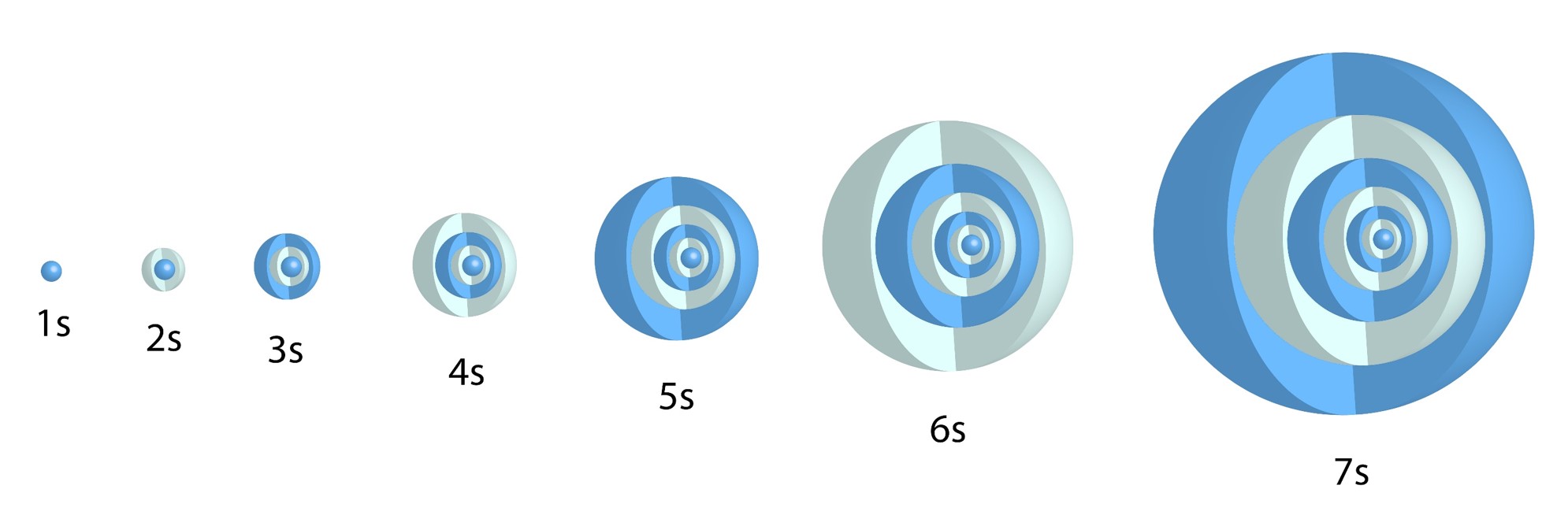
s Orbital:

$l=0,\ m_l=0$

One allowed value for $m_l$ = one type of s orbital for each value of n.

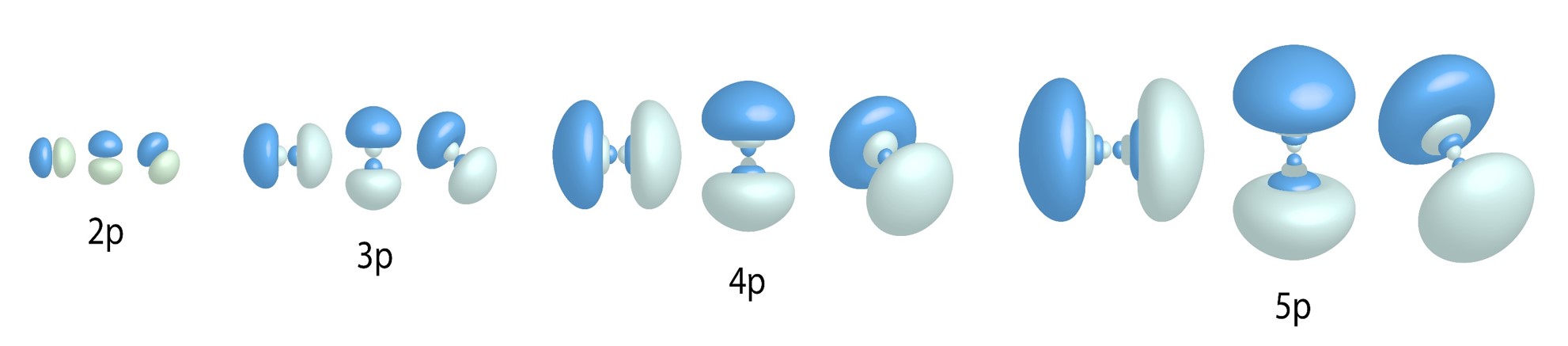
p Orbitals:

$l=0,\ m_l=-1,0,1$

Three allowed values for $m_l$ = three types of p orbitals for n values greater than and equal to two.

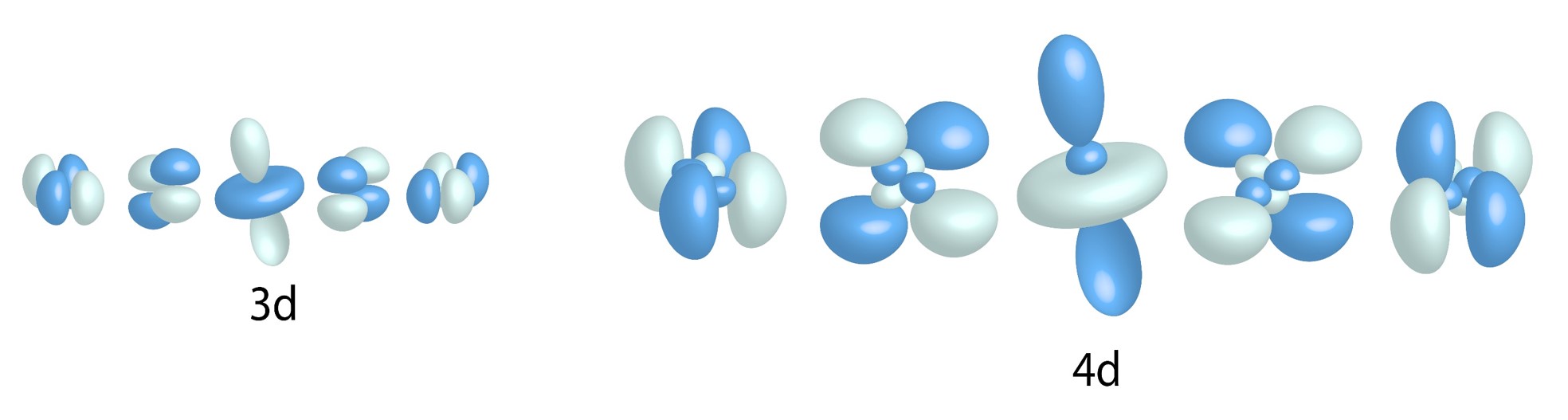
d Orbitals:

$l=0,\ m_l=-2,-1,0,1,2$

Five allowed values for $m_l$ = five types of d orbitals for n greater than and equal to three.

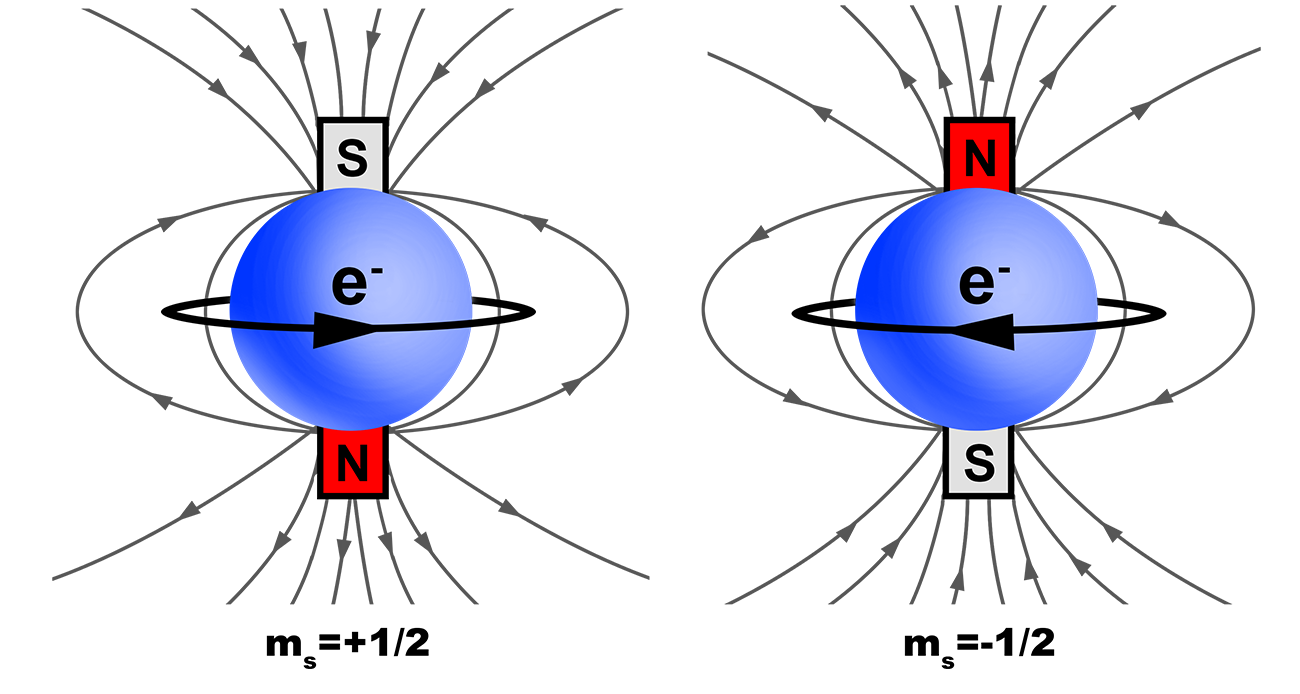
Spin Quantum Number 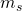$m_s$

Spin is intrinsic to all electrons, it is quantized, with only two orientations; spin up or spin down.

Value = $+\frac{1}{2}$ OR $-\frac{1}{2}$

Pauli Exclusion Principle

No two electrons in an atom can have the same four quantum numbers, however, Any three quantum numbers can be the same.

This implies: One orbital may contain two electrons of opposite spin orientation!

Aufbau Principle

In a one electron system the subshells are degenerate; meaning s,p,d,f,.., all have the same energy level in each shell. However, in a multi-electron atom the subshells have different energy levels.


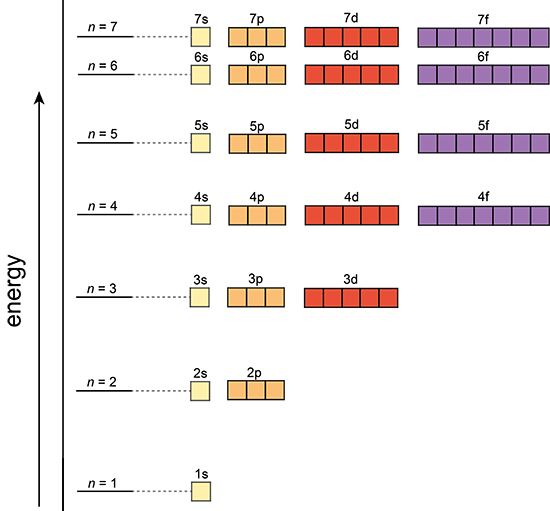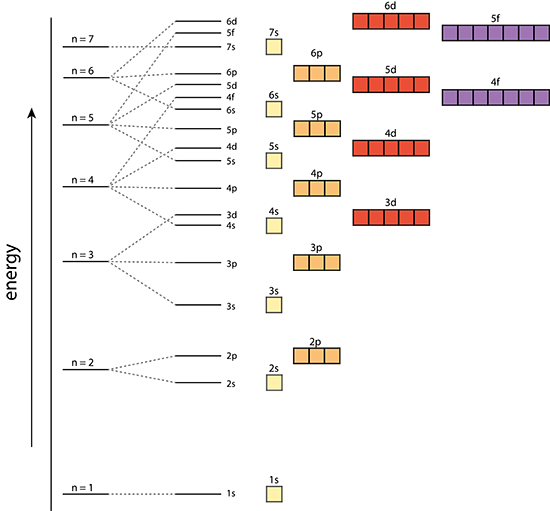Single electron atom	Multi-electron atom

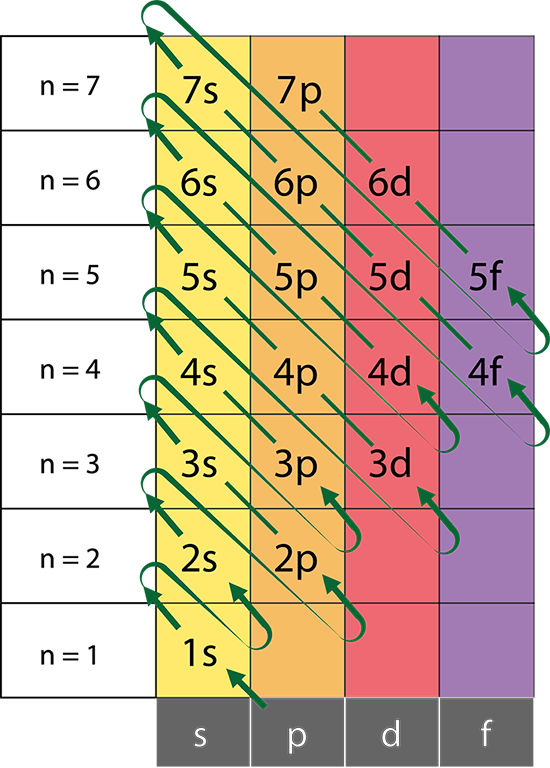
The Aufbau Principle:

That means that we want to know about a system in which the lower energy orbitals fill before the higher energy orbitals. This idea is referred to as the Aufbau principle, and the general order in which electrons fill orbitals in an atom to achieve the ground state configuration is: 1s,2s,2p,3s,3p,4s,3d,4p,5s,4d,5p,6s,4f,5d,6p,7s,5f,6d,7p

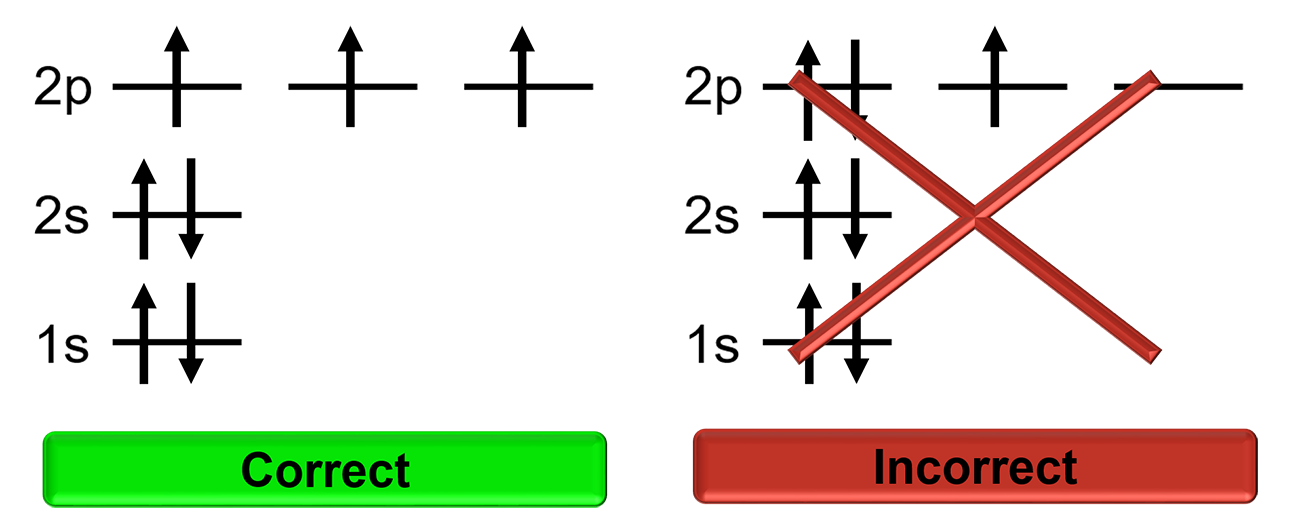
Hund’s Rule

Electrons will singly occupy degenerate orbitals until they are half full before pairing up with other electrons. Electrons in half full orbitals will have the same spin.

Electronic Configurations

A notation that represents the orbitals occupied by electrons in an atom.

Write the value of n, followed by the number of electrons allowed in each orbital until all electrons in the atom are assigned to an orbital.

Example Carbon: 6 electrons = $1s^{2}2s^{2}2p^{2}$

Core Electrons	Valence Electrons	Short-hand Electronic Configuration
Electrons in a filled inner shell.	Electrons in the outermost shell (highest n value). Example: Carbon 6 electrons = $\begin{table}[cc] 1s^{2} $ 2s^{2}2p^{2} // Core $ Valence \end{table}$	An electronic configuration using a noble gas to represent the filled shells and only writing out the valence electrons.

Orbital Diagrams

A diagram that represents the filled orbitals in an atom by denoting the electron as an arrow.

Each subshell is represented as a line or a circle, electrons are represented as arrows pointing up or down according to the electron’s spin.

Example Carbon: 6 electrons = $1s^{2}2s^{2}2p^{2}$

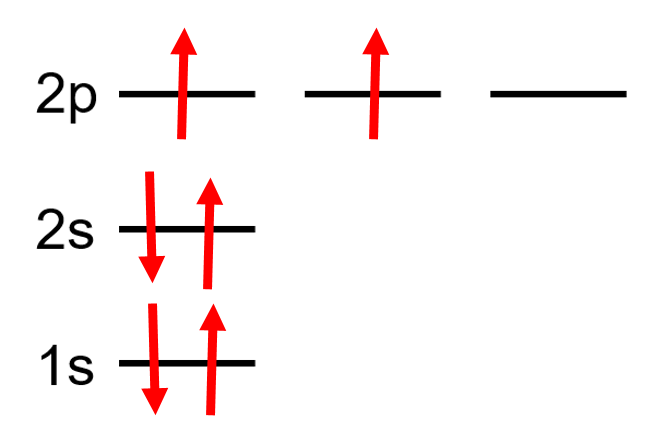Examples

The following video will help you understand electron configurations and orbital diagrams

Video Transcript

Problem Set

Below are two documents. One is practice problems, the second is the same problems with solutions.
They can be downloaded and changed to suit your needs.

Problem Set

Problem Set Solutions

Quiz

License

Icon for the Creative Commons Attribution 4.0 International License

Be Prepared! Everything you should know for 1st year Chemistry Copyright © by Andrew Vreugdenhil and Kelly Wright is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

The Atom

The Atom

Nucleus

Neutron

Proton

Electron

Charge

A neutral atom has the same number of protons as electrons.

Physical Properties of Sub-atomic Particles

Unified atomic mass units (u):

Atom Terminology

Z = number of protons = atomic number

A = number of protons + number of neutrons = mass number

Element

Chemical Symbol (X)

Atomic Number (Z)

Mass Number (A)

The number of protons defines the type of atom or element!

Isotopes

Isotopes are atoms of the same type that have the same number of protons and varying numbers of neutrons.

We know:

Isotopes:

Isotopes Example:

Atoms of an element that have a different number of neutrons.

28-14=14 neutrons

29-14=15 neutrons

30-14=16 neutrons

Isotope Notation

Including the atomic number is redundant when representing isotopes. It is common to use the following notation: X-A. For example: Si-28, Si-29, Si-30

Atomic Mass

We know:

Atomic Mass:

The atomic mass of an element as seen on the periodic table is a weighted average of isotopic masses of that element.

Atomic Mass Example:

This Copper (Cu) sample will contain approximately 30.83 % of Cu-65 and 69.17 % of Cu-63

Atomic Mass Calculations:

Atomic mass for an element can be calculated with the following formula:

In simple terms this formula is telling us that atomic mass can be calculated by:

An atomic mass calculation is included in the example section!

The Mole

A measurement similar to a pair, dozen or score. A pair is 2 objects, a dozen is 12 objects and a score is 20 objects.

Defining the Mole:

The mass of one mole of C-12 atoms is 12 g

Molar Mass:

Molar Mass of an Element:

The Periodic Table of Elements

Metals, Non-Metals and Metalloids

Periodic Trends

Metals:

Non-Metals:

Metalloids:

Main Group Elements and Transition Metals

Periodic Trends

Main Group:

Transition Metals:

Lanthanoids and Actinoids:

Groups and Periods of the Periodic Table

Periodic Trends

Ions

Common Main Group Ions:

We know:

Ions:

Ions and Groups:

Ions are charged particles that have gained or lost an electron(s).

Cation (+):

Anion (-):

Ion Notation:

Examples

Example Problem 1

Example Problem 2

These gold earrings have a mass of 1.00 g. Calculate the moles of gold in the earrings, how many gold atoms do the earrings contain? Assume the earrings are pure gold.

Problem Set

Below are two documents. One is practice problems, the second is the same problems with solutions. They can be downloaded and changed to suit your needs.

Quiz

Atomic Structure

Atom Models

Bohr Model of an Atom

Quantum Mechanical Model of an Atom

Schrodinger – Quantum Mechanical Models

Orbital:

Including the atomic number is redundant when representing isotopes. It is common to use the following notation: X-A.
For example: Si-28, Si-29, Si-30

Below are two documents. One is practice problems, the second is the same problems with solutions.
They can be downloaded and changed to suit your needs.

Magnetic Quantum Number $(m_l)$

Spin Quantum Number $m_s$

Below are two documents. One is practice problems, the second is the same problems with solutions.
They can be downloaded and changed to suit your needs.