4 Vector Geometry
4.1 Vectors and Lines
In this chapter we study the geometry of 3-dimensional space. We view a point in 3-space as an arrow from the origin to that point. Doing so provides a “picture” of the point that is truly worth a thousand words.
Vectors in 
Introduce a coordinate system in 3-dimensional space in the usual way. First, choose a point ![]() called the
called the ![]() , then choose three mutually perpendicular lines through
, then choose three mutually perpendicular lines through ![]() , called the
, called the ![]() ,
, ![]() , and
, and ![]() , and establish a number scale on each axis with zero at the origin. Given a point
, and establish a number scale on each axis with zero at the origin. Given a point ![]() in
in ![]() -space we associate three numbers
-space we associate three numbers ![]() ,
, ![]() , and
, and ![]() with
with ![]() , as described in Figure 4.1.1.
, as described in Figure 4.1.1.
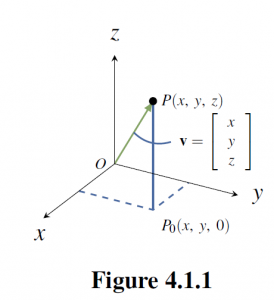
These numbers are called the ![]() of
of ![]() , and we denote the point as
, and we denote the point as ![]() , or
, or ![]() to emphasize the label
to emphasize the label ![]() . The result is called a
. The result is called a ![]() coordinate system for 3-space, and the resulting description of 3-space is called
coordinate system for 3-space, and the resulting description of 3-space is called ![]() .
.
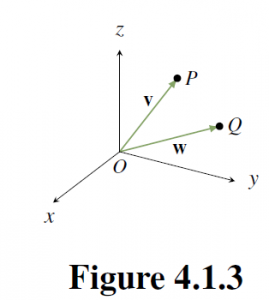
As in the plane, we introduce vectors by identifying each point ![]() with the vector
with the vector
![Rendered by QuickLaTeX.com \vec{v} = \left[ \begin{array}{c} x \\ y \\ z \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-80ba3720048641eb9eba0cf5ad768762_l3.png) in
in ![]() , represented by the
, represented by the ![]() from the origin to
from the origin to ![]() as in Figure 4.1.1. Informally, we say that the point
as in Figure 4.1.1. Informally, we say that the point ![]() has vector
has vector ![]() , and that vector
, and that vector ![]() has point
has point ![]() . In this way 3-space is identified with
. In this way 3-space is identified with ![]() , and this identification will be made throughout this chapter, often without comment. In particular, the terms “vector” and “point” are interchangeable. The resulting description of 3-space is called
, and this identification will be made throughout this chapter, often without comment. In particular, the terms “vector” and “point” are interchangeable. The resulting description of 3-space is called ![]() . Note that the origin is
. Note that the origin is ![Rendered by QuickLaTeX.com \vec{0} = \left[ \begin{array}{c} 0 \\ 0 \\ 0 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-30b3e2a1a83469a70aafe843db8bd0fb_l3.png) .
.
Length and direction
We are going to discuss two fundamental geometric properties of vectors in ![]() : length and direction. First, if
: length and direction. First, if ![]() is a vector with point
is a vector with point ![]() , the
, the ![]() of vector
of vector ![]() is defined to be the distance from the origin to
is defined to be the distance from the origin to ![]() , that is the length of the arrow representing
, that is the length of the arrow representing ![]() . The following properties of length will be used frequently.
. The following properties of length will be used frequently.
Theorem 4.1.1
Let ![Rendered by QuickLaTeX.com \vec{v} = \left[ \begin{array}{c} x \\ y \\ z \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-80ba3720048641eb9eba0cf5ad768762_l3.png) be a vector.
be a vector.
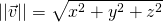 .
.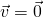 if and only if
if and only if 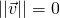
 for all scalars
for all scalars  .
.
Proof:
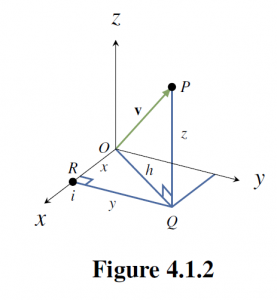
Let ![]() have point
have point ![]() .
.
- In Figure 4.1.2,
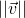 is the hypotenuse of the right triangle
is the hypotenuse of the right triangle 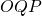 , and so
, and so 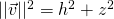 by Pythagoras’ theorem. But
by Pythagoras’ theorem. But 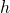 is the hypotenuse of the right triangle
is the hypotenuse of the right triangle  , so
, so 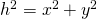 . Now (1) follows by eliminating
. Now (1) follows by eliminating  and taking positive square roots.
and taking positive square roots. - If
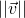 = 0, then
= 0, then 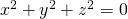 by (1). Because squares of real numbers are nonnegative, it follows that
by (1). Because squares of real numbers are nonnegative, it follows that 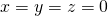 , and hence that
, and hence that 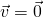 . The converse is because
. The converse is because  .
. - We have
![Rendered by QuickLaTeX.com a\vec{v} = \left[ \begin{array}{ccc} ax & ay & az \end{array}\right]^{T}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-4ce9697bffaf4a853d6977ba8cc6e4c5_l3.png) so (1) gives
so (1) gives
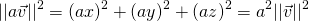
Hence
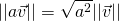 , and we are done because
, and we are done because 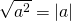 for any real number
for any real number  .
.
Example 4.1.1
If ![Rendered by QuickLaTeX.com \vec{v} = \left[ \begin{array}{r} 2 \\ -3 \\ 3 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-b4b932d4ab112913c9fc5b4e59fea0d5_l3.png)
then ![]() . Similarly if
. Similarly if ![]()
in 2-space then ![]() .
.
When we view two nonzero vectors as arrows emanating from the origin, it is clear geometrically what we mean by saying that they have the same or opposite ![]() . This leads to a fundamental new description of vectors.
. This leads to a fundamental new description of vectors.
Theorem 4.1.2
Let ![]() and
and ![]() be vectors in
be vectors in ![]() . Then
. Then ![]() as matrices if and only if
as matrices if and only if ![]() and
and ![]() have the same direction and the same length.
have the same direction and the same length.
Proof:
If ![]() , they clearly have the same direction and length. Conversely, let
, they clearly have the same direction and length. Conversely, let ![]() and
and ![]() be vectors with points
be vectors with points ![]() and
and ![]() respectively. If
respectively. If ![]() and
and ![]() have the same length and direction then, geometrically,
have the same length and direction then, geometrically, ![]() and
and ![]() must be the same point.
must be the same point.
Hence ![]() ,
, ![]() , and
, and ![]() , that is
, that is ![Rendered by QuickLaTeX.com \vec{v} = \left[ \begin{array}{c} x \\ y \\ z \end{array} \right] = \left[ \begin{array}{c} x_{1} \\ y_{1} \\ z_{1} \end{array} \right] = \vec{w}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-faeab418ff270d20ea560d22bc4cfd2b_l3.png) .
.
Note that a vector’s length and direction do ![]() depend on the choice of coordinate system in
depend on the choice of coordinate system in ![]() . Such descriptions are important in applications because physical laws are often stated in terms of vectors, and these laws cannot depend on the particular coordinate system used to describe the situation.
. Such descriptions are important in applications because physical laws are often stated in terms of vectors, and these laws cannot depend on the particular coordinate system used to describe the situation.
Geometric Vectors
If ![]() and
and ![]() are distinct points in space, the arrow from
are distinct points in space, the arrow from ![]() to
to ![]() has length and direction.
has length and direction.

Hence,
Definition 4.1 Geometric vectors
Suppose that ![]() and
and ![]() are any two points in
are any two points in ![]() . In Figure 4.1.4 the line segment from
. In Figure 4.1.4 the line segment from ![]() to
to ![]() is denoted
is denoted ![]() and is called the
and is called the ![]() from
from ![]() to
to ![]() . Point
. Point ![]() is called the
is called the ![]() of
of ![]() ,
, ![]() is called the
is called the ![]() and the
and the ![]() is denoted
is denoted ![]() .
.
Note that if ![]() is any vector in
is any vector in ![]() with point
with point ![]() then
then ![]() is itself a geometric vector where
is itself a geometric vector where ![]() is the origin. Referring to
is the origin. Referring to ![]() as a “vector” seems justified by Theorem 4.1.2 because it has a direction (from
as a “vector” seems justified by Theorem 4.1.2 because it has a direction (from ![]() to
to ![]() ) and a length
) and a length ![]() . However there appears to be a problem because two geometric vectors can have the same length and direction even if the tips and tails are different.
. However there appears to be a problem because two geometric vectors can have the same length and direction even if the tips and tails are different.
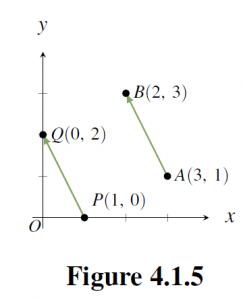
For example ![]() and
and ![]() in Figure 4.1.5 have the same length
in Figure 4.1.5 have the same length ![]() and the same direction (1 unit left and 2 units up) so, by Theorem 4.1.2, they are the same vector! The best way to understand this apparent paradox is to see
and the same direction (1 unit left and 2 units up) so, by Theorem 4.1.2, they are the same vector! The best way to understand this apparent paradox is to see ![]() and
and ![]() as different
as different ![]() of the same underlying vector
of the same underlying vector ![]() . Once it is clarified, this phenomenon is a great benefit because, thanks to Theorem 4.1.2, it means that the same geometric vector can be positioned anywhere in space; what is important is the length and direction, not the location of the tip and tail. This ability to move geometric vectors about is very useful.
. Once it is clarified, this phenomenon is a great benefit because, thanks to Theorem 4.1.2, it means that the same geometric vector can be positioned anywhere in space; what is important is the length and direction, not the location of the tip and tail. This ability to move geometric vectors about is very useful.
The Parallelogram Law

We now give an intrinsic description of the sum of two vectors ![]() and
and ![]() in
in ![]() , that is a description that depends only on the lengths and directions of
, that is a description that depends only on the lengths and directions of ![]() and
and ![]() and not on the choice of coordinate system. Using Theorem 4.1.2 we can think of these vectors as having a common tail
and not on the choice of coordinate system. Using Theorem 4.1.2 we can think of these vectors as having a common tail ![]() . If their tips are
. If their tips are ![]() and
and ![]() respectively, then they both lie in a plane
respectively, then they both lie in a plane ![]() containing
containing ![]() ,
, ![]() , and
, and ![]() , as shown in Figure 4.1.6. The vectors
, as shown in Figure 4.1.6. The vectors ![]() and
and ![]() create a parallelogram in
create a parallelogram in ![]() , shaded in Figure 4.1.6, called the parallelogram
, shaded in Figure 4.1.6, called the parallelogram ![]() by
by ![]() and
and ![]() .
.
If we now choose a coordinate system in the plane ![]() with
with ![]() as origin, then the parallelogram law in the plane shows that their sum
as origin, then the parallelogram law in the plane shows that their sum ![]() is the diagonal of the parallelogram they determine with tail
is the diagonal of the parallelogram they determine with tail ![]() . This is an intrinsic description of the sum
. This is an intrinsic description of the sum ![]() because it makes no reference to coordinates. This discussion proves:
because it makes no reference to coordinates. This discussion proves:
The Parallelogram Law
In the parallelogram determined by two vectors ![]() and
and ![]() , the vector
, the vector ![]() is the diagonal with the same tail as
is the diagonal with the same tail as ![]() and
and ![]() .
.
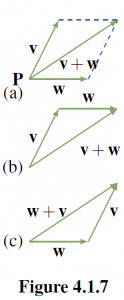
Because a vector can be positioned with its tail at any point, the parallelogram law leads to another way to view vector addition. In Figure 4.1.7 (a) the sum ![]() of two vectors
of two vectors ![]() and
and ![]() is shown as given by the parallelogram law. If
is shown as given by the parallelogram law. If ![]() is moved so its tail coincides with the tip of
is moved so its tail coincides with the tip of ![]() (shown in (b)) then the sum
(shown in (b)) then the sum ![]() is seen as “first
is seen as “first ![]() and then
and then ![]() . Similarly, moving the tail of
. Similarly, moving the tail of ![]() to the tip of
to the tip of ![]() shows in (c) that
shows in (c) that ![]() is “first
is “first ![]() and then
and then ![]() .” This will be referred to as the
.” This will be referred to as the ![]() , and it gives a graphic illustration of why
, and it gives a graphic illustration of why ![]() .
.
Since ![]() denotes the vector from a point
denotes the vector from a point ![]() to a point
to a point ![]() , the tip-to-tail rule takes the easily remembered form
, the tip-to-tail rule takes the easily remembered form
![]()
for any points ![]() ,
, ![]() , and
, and ![]() .
.
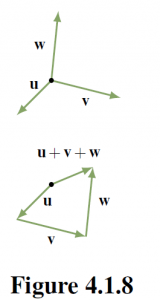
One reason for the importance of the tip-to-tail rule is that it means two or more vectors can be added by placing them tip-to-tail in sequence. This gives a useful “picture” of the sum of several vectors, and is illustrated for three vectors in Figure 4.1.8 where ![]() is viewed as first
is viewed as first ![]() , then
, then ![]() , then
, then ![]() .
.
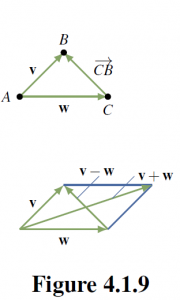
There is a simple geometrical way to visualize the (matrix) ![]()
![]() of two vectors. If
of two vectors. If ![]() and
and ![]() are positioned so that they have a common tail
are positioned so that they have a common tail ![]() , and if
, and if ![]() and
and ![]() are their respective tips, then the tip-to-tail rule gives
are their respective tips, then the tip-to-tail rule gives ![]() . Hence
. Hence ![]() is the vector from the tip of
is the vector from the tip of ![]() to the tip of
to the tip of ![]() . Thus both
. Thus both ![]() and
and ![]() appear as diagonals in the parallelogram determined by
appear as diagonals in the parallelogram determined by ![]() and
and ![]() (see Figure 4.1.9.
(see Figure 4.1.9.
Theorem 4.1.3
If ![]() and
and ![]() have a common tail, then
have a common tail, then ![]() is the vector from the tip of
is the vector from the tip of ![]() to the tip of
to the tip of ![]() .
.
One of the most useful applications of vector subtraction is that it gives a simple formula for the vector from one point to another, and for the distance between the points.
Theorem 4.1.4
Let ![]() and
and ![]() be two points. Then:
be two points. Then:
![Rendered by QuickLaTeX.com \vec{P_{1}P}_{2} = \left[ \begin{array}{c} x_{2} - x_{1} \\ y_{2} - y_{1} \\ z_{2} - z_{1} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-0d91b62f61e2ab368818c961ede56673_l3.png) .
.- The distance between
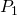 and
and 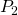 is
is 
Can you prove these results?
Example 4.1.3
The distance between ![]() and
and ![]() is
is ![]() , and the vector from
, and the vector from ![]() to
to ![]() is
is
![Rendered by QuickLaTeX.com \vec{P_{1}P}_{2} = \left[ \begin{array}{r} -1 \\ 2 \\ 1 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-4f11ea97f1984fb31df5e2ab319e7104_l3.png) .
.
The next theorem tells us what happens to the length and direction of a scalar multiple of a given vector.
Scalar Multiple Law
If a is a real number and ![]() is a vector then:
is a vector then:
- The length of
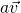 is
is 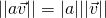 .
. - If
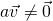 , the direction of
, the direction of 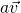 is the same as
is the same as  if
if  ; opposite to
; opposite to  if
if 
Proof:
The first statement is true due to Theorem 4.1.1.
To prove the second statement, let ![]() denote the origin in
denote the origin in ![]() Let
Let ![]() have point
have point ![]() , and choose any plane containing
, and choose any plane containing ![]() and
and ![]() . If we set up a coordinate system in this plane with
. If we set up a coordinate system in this plane with ![]() as origin, then
as origin, then ![]() so the result follows from the scalar multiple law in the plane.
so the result follows from the scalar multiple law in the plane.
A vector ![]() is called a
is called a ![]() if
if ![]() . Then
. Then
![Rendered by QuickLaTeX.com \vec{i} = \left[ \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f4675ab4908dccc00c63fa4377ec2134_l3.png) ,
, ![Rendered by QuickLaTeX.com \vec{j} = \left[ \begin{array}{c} 0 \\ 1 \\ 0 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-247115bfd0abd328188d22d4d7729d86_l3.png) , and
, and ![Rendered by QuickLaTeX.com \vec{k} = \left[ \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-6b34f73e2b2c16fd6b2cda1d7ece4bf0_l3.png)
are unit vectors, called the ![]() vectors.
vectors.
Example 4.1.4
If ![]() show that
show that ![]() is the unique unit vector in the same direction as
is the unique unit vector in the same direction as ![]()
Solution:
The vectors in the same direction as ![]() are the scalar multiples
are the scalar multiples ![]() where
where ![]() . But
. But ![]() when
when ![]() , so
, so ![]() is a unit vector if and only if
is a unit vector if and only if ![]() .
.
Definition 4.2 Parallel vectors in ![]()
Two nonzero vectors are called ![]() if they have the same or opposite direction.
if they have the same or opposite direction.
Theorem 4.1.5
Two nonzero vectors ![]() and
and ![]() are parallel if and only if one is a scalar multiple of the other.
are parallel if and only if one is a scalar multiple of the other.
Example 4.1.5
Given points ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , determine if
, determine if ![]() and
and ![]() are parallel.
are parallel.
Solution:
By Theorem 4.1.3, ![]() and
and ![]() . If
. If ![]()
then ![]() , so
, so ![]() and
and ![]() , which is impossible. Hence
, which is impossible. Hence ![]() is
is ![]() a scalar multiple of
a scalar multiple of ![]() , so these vectors are not parallel by Theorem 4.1.5.
, so these vectors are not parallel by Theorem 4.1.5.
Lines in Space
These vector techniques can be used to give a very simple way of describing straight lines in space. In order to do this, we first need a way to
specify the orientation of such a line.
Definition 4.3 Direction Vector of a Line
We call a nonzero vector ![]() a direction vector for the line if it is parallel to
a direction vector for the line if it is parallel to ![]() for some pair of distinct points
for some pair of distinct points ![]() and
and ![]() on the line.
on the line.
Note that any nonzero scalar multiple of ![]() would also serve as a direction vector of the line.
would also serve as a direction vector of the line.
We use the fact that there is exactly one line that passes through a particular point ![]() and has a given direction vector
and has a given direction vector
![Rendered by QuickLaTeX.com \vec{d} = \left[ \begin{array}{c} a \\ b \\ c \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-ec3f3226d3e1112c9896e325903c769f_l3.png) . We want to describe this line by giving a condition on
. We want to describe this line by giving a condition on ![]() ,
, ![]() , and
, and ![]() that the point
that the point ![]() lies on this line. Let
lies on this line. Let
![Rendered by QuickLaTeX.com \vec{p}_{0} = \left[ \begin{array}{c} x_{0} \\ y_{0} \\ z_{0} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-6ad903adbe0411494705af4e8f5ef084_l3.png)
and ![Rendered by QuickLaTeX.com \vec{p} = \left[ \begin{array}{c} x \\ y \\ z \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-94351a7c5397f16180d12b7ac8619c8c_l3.png) denote the vectors of
denote the vectors of ![]() and
and ![]() , respectively.
, respectively.

Then
![]()
Hence ![]() lies on the line if and only if
lies on the line if and only if ![]() is parallel to
is parallel to ![]() —that is, if and only if
—that is, if and only if ![]() for some scalar
for some scalar ![]() by Theorem 4.1.5. Thus
by Theorem 4.1.5. Thus ![]() is the vector of a point on the line if and only if
is the vector of a point on the line if and only if ![]() for some scalar
for some scalar ![]() .
.
Vector Equation of a line
The line parallel to ![]() through the point with vector
through the point with vector ![]() is given by
is given by
![]()
In other words, the point ![]() with vector
with vector ![]() is on this line if and only if a real number t exists such that
is on this line if and only if a real number t exists such that ![]() .
.
In component form the vector equation becomes
![Rendered by QuickLaTeX.com \begin{equation*} \left[ \begin{array}{c} x \\ y \\ z \end{array} \right] = \left[ \begin{array}{c} x_{0} \\ y_{0} \\ z_{0} \end{array} \right] + t \left[ \begin{array}{c} a \\ b \\ c \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-913ee00b2bc4988c7904bf047f87fc13_l3.png)
Equating components gives a different description of the line.
Parametric Equations of a line
The line through ![]() with direction vector
with direction vector
![Rendered by QuickLaTeX.com \vec{d} = \left[ \begin{array}{c} a \\ b \\ c \end{array} \right] \neq \vec{0}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-28eca1be57947254a98ec01d662baab9_l3.png) is given by
is given by
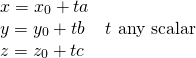
In other words, the point ![]() is on this line if and only if a real number
is on this line if and only if a real number ![]() exists such that
exists such that ![]() ,
, ![]() , and
, and ![]() .
.
Example 4.1.6
Find the equations of the line through the points ![]() and
and ![]() .
.
Solution:
Let
![Rendered by QuickLaTeX.com \vec{d} = \vec{P_{0}P}_{1} = \left[ \begin{array}{c} 2 \\ 1 \\ 0 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-4810a1f6d35bb92109008d73ff2d7f2a_l3.png)
denote the vector from ![]() to
to ![]() . Then
. Then ![]() is parallel to the line (
is parallel to the line (![]() and
and ![]() are on the line), so
are on the line), so ![]() serves as a direction vector for the line. Using
serves as a direction vector for the line. Using ![]() as the point on the line leads to the parametric equations
as the point on the line leads to the parametric equations
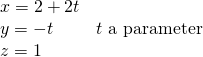
Note that if ![]() is used (rather than
is used (rather than ![]() ), the equations are
), the equations are
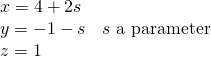
These are different from the preceding equations, but this is merely the result of a change of parameter. In fact, ![]() .
.
Example 4.1.7
Determine whether the following lines intersect and, if so, find the point of intersection.

Solution:
Suppose ![]() with vector
with vector ![]() lies on both lines. Then
lies on both lines. Then
![Rendered by QuickLaTeX.com \begin{equation*} \left[ \begin{array}{c} 1 - 3t \\ 2 + 5t \\ 1 + t \end{array} \right] = \left[ \begin{array}{c} x \\ y \\ z \end{array} \right] = \left[ \begin{array}{c} -1 + s \\ 3 - 4s \\ 1 - s \end{array} \right] \mbox{ for some } t \mbox{ and } s, \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f905eedb03545c1d8a45db08b6ebeef6_l3.png)
where the first (second) equation is because ![]() lies on the first (second) line. Hence the lines intersect if and only if the three equations
lies on the first (second) line. Hence the lines intersect if and only if the three equations
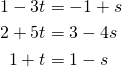
have a solution. In this case, ![]() and
and ![]() satisfy all three equations, so the lines do intersect and the point of intersection is
satisfy all three equations, so the lines do intersect and the point of intersection is
![Rendered by QuickLaTeX.com \begin{equation*} \vec{p} = \left[ \begin{array}{c} 1 - 3t \\ 2 + 5t \\ 1 + t \end{array} \right] = \left[ \begin{array}{r} -2 \\ 7 \\ 2 \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-0040d1e22ad92cc9b05a2e7d53180ef3_l3.png)
using ![]() . Of course, this point can also be found from
. Of course, this point can also be found from
![Rendered by QuickLaTeX.com \vec{p} = \left[ \begin{array}{c} -1 + s \\ 3 - 4s \\ 1 - s \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-4d91258eaf2175b078cb37691b1d8fa5_l3.png) using
using ![]() .
.
4.2 Projections and Planes
Suppose a point ![]() and a plane are given and it is desired to find the point
and a plane are given and it is desired to find the point ![]() that lies in the plane and is closest to
that lies in the plane and is closest to ![]() , as shown in Figure 4.2.1.
, as shown in Figure 4.2.1.
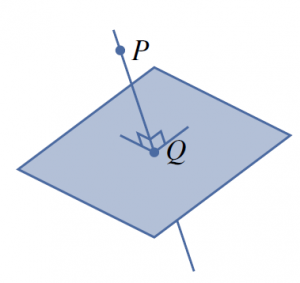
Clearly, what is required is to find the line through ![]() that is perpendicular to the plane and then to obtain
that is perpendicular to the plane and then to obtain ![]() as the point of intersection of this line with the plane. Finding the line perpendicular to the plane requires a way to determine when two vectors are perpendicular. This can be done using the idea of the dot product of two vectors.
as the point of intersection of this line with the plane. Finding the line perpendicular to the plane requires a way to determine when two vectors are perpendicular. This can be done using the idea of the dot product of two vectors.
The Dot Product and Angles
Definition 4.4 Dot Product in ![]()
Given vectors
![Rendered by QuickLaTeX.com \vec{v} = \left[ \begin{array}{c} x_{1} \\ y_{1}\\ z_{1} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-ccc7d26a8ee7d698dd1d48eaefd0f0e5_l3.png) and
and
![Rendered by QuickLaTeX.com \vec{w} = \left[ \begin{array}{c} x_{2} \\ y_{2}\\ z_{2} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-70280013eed5b9fc9490c20eeaeb7542_l3.png) , their dot product
, their dot product ![]() is a number defined
is a number defined
![]()
Because ![]() is a number, it is sometimes called the scalar product of
is a number, it is sometimes called the scalar product of ![]() and
and ![]()
Example 4.2.1
If ![Rendered by QuickLaTeX.com \vec{v} = \left[ \begin{array}{r} 2 \\ -1 \\ 3 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-7c0f43e3bdf79d6d2cce2b685b867aaa_l3.png)
and ![Rendered by QuickLaTeX.com \vec{w} = \left[ \begin{array}{r} 1 \\ 4\\ -1 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-4fe5be9b5f6bc750aac3b0ef910233fa_l3.png) , then
, then ![]() .
.
Theorem 4.2.1
Let ![]() ,
, ![]() , and
, and ![]() denote vectors in
denote vectors in ![]() (or
(or ![]() ).
).
 is a real number.
is a real number.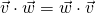 .
.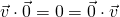 .
.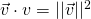 .
.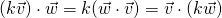 for all scalars
for all scalars 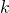 .
.
The readers are invited to prove these properties using the definition of dot products.
Example 4.2.2
Verify that ![]() when
when ![]() ,
, ![]() , and
, and ![]() .
.
Solution:
We apply Theorem 4.2.1 several times:
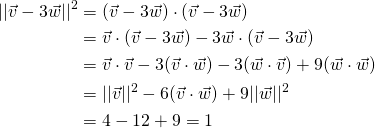
There is an intrinsic description of the dot product of two nonzero vectors in ![]() . To understand it we require the following result from trigonometry.
. To understand it we require the following result from trigonometry.
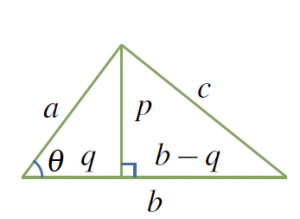
Laws of Cosine
If a triangle has sides ![]() ,
, ![]() , and
, and ![]() , and if
, and if ![]() is the interior angle opposite
is the interior angle opposite ![]() then
then
![]()
Proof:
We prove it when is ![]() acute, that is
acute, that is ![]() ; the obtuse case is similar. In Figure 4.2.2 we have
; the obtuse case is similar. In Figure 4.2.2 we have ![]() and
and ![]() .
.
Hence Pythagoras’ theorem gives
![]()
The law of cosines follows because ![]() for any angle
for any angle ![]() .
.
Note that the law of cosines reduces to Pythagoras’ theorem if ![]() is a right angle (because
is a right angle (because ![]() ).
).
Now let ![]() and
and ![]() be nonzero vectors positioned with a common tail. Then they determine a unique angle
be nonzero vectors positioned with a common tail. Then they determine a unique angle ![]() in the range
in the range
![]()
This angle ![]() will be called the angle between
will be called the angle between ![]() and
and ![]() . Clearly
. Clearly ![]() and
and ![]() are parallel if
are parallel if ![]() is either
is either ![]() or
or ![]() . Note that we do not define the angle between
. Note that we do not define the angle between ![]() and
and ![]() if one of these vectors is
if one of these vectors is ![]() .
.
The next result gives an easy way to compute the angle between two nonzero vectors using the dot product.
Theorem 4.2.2
Let ![]() and
and ![]() be nonzero vectors. If
be nonzero vectors. If ![]() is the angle between
is the angle between ![]() and
and ![]() , then
, then
![]()
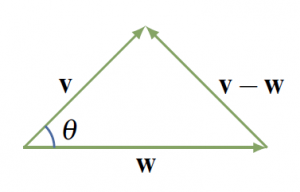
Proof:
We calculate ![]() in two ways. First apply the law of cosines to the triangle in Figure 4.2.4 to obtain:
in two ways. First apply the law of cosines to the triangle in Figure 4.2.4 to obtain:
![]()
On the other hand, we use Theorem 4.2.1:
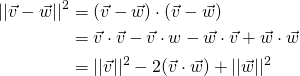
Comparing these we see that ![]() , and the result follows.
, and the result follows.
If ![]() and
and ![]() are nonzero vectors, Theorem 4.2.2 gives an intrinsic description of
are nonzero vectors, Theorem 4.2.2 gives an intrinsic description of ![]() because
because ![]() ,
, ![]() , and the angle
, and the angle ![]() between
between ![]() and
and ![]() do not depend on the choice of coordinate system. Moreover, since
do not depend on the choice of coordinate system. Moreover, since ![]() and
and ![]() are nonzero (
are nonzero (![]() and
and ![]() are nonzero vectors), it gives a formula for the cosine of the angle
are nonzero vectors), it gives a formula for the cosine of the angle ![]() :
:
![]()
Since ![]() , this can be used to find
, this can be used to find ![]() .
.
Example 4.2.3
Compute the angle between
![Rendered by QuickLaTeX.com \vec{u} = \left[ \begin{array}{r} -1 \\ 1 \\ 2 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-93f90b07b74ac41fc0efde25cb24acca_l3.png) and
and
![Rendered by QuickLaTeX.com \vec{v} = \left[ \begin{array}{r} 2 \\ 1 \\ -1 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-2688c17ee8f7b48b529b8e9c5c0ce619_l3.png) .
.
Solution:
Compute ![]() . Now recall that
. Now recall that ![]() and
and ![]() are defined so that (
are defined so that (![]() ,
, ![]() ) is the point on the unit circle determined by the angle
) is the point on the unit circle determined by the angle ![]() (drawn counterclockwise, starting from the positive
(drawn counterclockwise, starting from the positive ![]() axis). In the present case, we know that
axis). In the present case, we know that ![]() and that
and that ![]() . Because
. Because ![]() , it follows that
, it follows that ![]() .
.
If ![]() and
and ![]() are nonzero, the previous example shows that
are nonzero, the previous example shows that ![]() has the same sign as
has the same sign as ![]() , so
, so
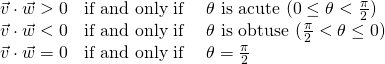
In this last case, the (nonzero) vectors are perpendicular. The following terminology is used in linear algebra:
Definition 4.5 Orthogonal Vectors in ![]()
Two vectors ![]() and
and ![]() are said to be \textbf{orthogonal}\index{orthogonal vectors}\index{vectors!orthogonal vectors} if
are said to be \textbf{orthogonal}\index{orthogonal vectors}\index{vectors!orthogonal vectors} if ![]() or
or ![]() or the angle between them is
or the angle between them is ![]() .
.
Since ![]() if either
if either ![]() or
or ![]() , we have the following theorem:
, we have the following theorem:
Theorem 4.2.3
Two vectors ![]() and
and ![]() are orthogonal if and only if
are orthogonal if and only if ![]() .
.
Example 4.2.4
Show that the points ![]() ,
, ![]() , and
, and ![]() are the vertices of a right triangle.
are the vertices of a right triangle.
Solution:
The vectors along the sides of the triangle are
![Rendered by QuickLaTeX.com \begin{equation*} \vec{PQ} = \left[ \begin{array}{r} 1 \\ 2 \\ 3 \end{array} \right],\ \vec{PR} = \left[ \begin{array}{r} 3 \\ 1 \\ 3 \end{array} \right], \mbox{ and } \vec{QR} = \left[ \begin{array}{r} 2 \\ -1 \\ 0 \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-3e3b1c1d081b9ec86e5528232093cf76_l3.png)
Evidently ![]() , so
, so ![]() and
and ![]() are orthogonal vectors. This means sides
are orthogonal vectors. This means sides ![]() and
and ![]() are perpendicular—that is, the angle at
are perpendicular—that is, the angle at ![]() is a right angle.
is a right angle.
Projections
In applications of vectors, it is frequently useful to write a vector as the sum of two orthogonal vectors.
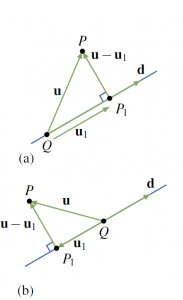
If a nonzero vector ![]() is specified, the key idea is to be able to write an arbitrary vector
is specified, the key idea is to be able to write an arbitrary vector ![]() as a sum of two vectors,
as a sum of two vectors,
![]()
where ![]() is parallel to
is parallel to ![]() and
and ![]() is orthogonal to
is orthogonal to ![]() . Suppose that
. Suppose that ![]() and
and ![]() emanate from a common tail
emanate from a common tail ![]() (see Figure 4.2.5). Let
(see Figure 4.2.5). Let ![]() be the tip of
be the tip of ![]() , and let
, and let ![]() denote the foot of the perpendicular from
denote the foot of the perpendicular from ![]() to the line through
to the line through ![]() parallel to
parallel to ![]() .
.
Then ![]() has the required properties:
has the required properties:
1. ![]() is parallel to
is parallel to ![]() .
.
2. ![]() is orthogonal to
is orthogonal to ![]() .
.
3. ![]() .
.
Definition 4.6 Projection in ![]()
The vector ![]() in Figure 4.2.6 is called the projection of
in Figure 4.2.6 is called the projection of ![]() on
on ![]() .
.
It is denoted
![]()
In Figure 4.2.5 (a) the vector ![]() has the same direction as
has the same direction as ![]() ; however,
; however, ![]() and
and ![]() have opposite directions if the angle between
have opposite directions if the angle between ![]() and
and ![]() is greater than
is greater than ![]() (see Figure 4.2.5 (b)). Note that the projection
(see Figure 4.2.5 (b)). Note that the projection ![]() is zero if and only if
is zero if and only if ![]() and
and ![]() are orthogonal.
are orthogonal.
Calculating the projection of ![]() on
on ![]() is remarkably easy.
is remarkably easy.
Theorem 4.2.4
Let ![]() and
and ![]() be vectors.
be vectors.
- The projection of
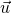 on
on 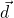 is given by
is given by  .
. - The vector
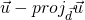 is orthogonal to
is orthogonal to 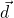 .
.
Proof:
The vector ![]() is parallel to
is parallel to ![]() and so has the form
and so has the form ![]() for some scalar
for some scalar ![]() . The requirement that
. The requirement that ![]() and
and ![]() are orthogonal determines
are orthogonal determines ![]() . In fact, it means that
. In fact, it means that ![]() by Theorem 4.2.3. If
by Theorem 4.2.3. If ![]() is substituted here, the condition is
is substituted here, the condition is
![]()
It follows that ![]() , where the assumption that
, where the assumption that ![]() guarantees that
guarantees that ![]() .
.
Example 4.2.5
Find the projection of
![Rendered by QuickLaTeX.com \vec{u} = \left[ \begin{array}{r} 2 \\ -3 \\ 1 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-0bb860cb56cb147d36cb34352a55bf1f_l3.png)
on ![Rendered by QuickLaTeX.com \vec{d} = \left[ \begin{array}{r} 1\\ -1 \\ 3 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-7c1cfdacba1089d8c65ea6ff7c57b9aa_l3.png)
and express ![]() where
where ![]() is parallel to
is parallel to ![]() and
and ![]() is orthogonal to
is orthogonal to ![]() .
.
Solution:
The projection ![]() of
of ![]() on
on ![]() is
is
![Rendered by QuickLaTeX.com \begin{equation*} \vec{u}_{1} = proj_{\vec{d}}{\vec{u}} = \frac{\vec{u} \cdot \vec{d}}{|| \vec{d}|| ^2}\vec{d} = \frac{2 + 3 + 3}{1^2 + (-1)^2 + 3^2} \left[ \begin{array}{r} 1\\ -1 \\ 3 \end{array} \right] = \frac{8}{11}\left[ \begin{array}{r} 1\\ -1 \\ 3 \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-229e18f2b977031aa3cad7ce46bd7fa9_l3.png)
Hence ![Rendered by QuickLaTeX.com \vec{u}_{2} = \vec{u} - \vec{u}_{1} = \frac{1}{11}\left[ \begin{array}{r} 14\\ -25 \\ -13 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d355e039a801512cbfd7c8d63343162c_l3.png) , and this is orthogonal to
, and this is orthogonal to ![]() by Theorem 4.2.4 (alternatively, observe that
by Theorem 4.2.4 (alternatively, observe that ![]() ). Since
). Since ![]() , we are done.
, we are done.
Note that the idea of projections can be used to find the shortest distance from a point to a straight line in ![]() which is
which is ![]() the length of the vector that’s orthogonal to the direction vector of the line.
the length of the vector that’s orthogonal to the direction vector of the line.
Planes
Definition 4.7 Normal vector in a plane
A nonzero vector ![]() is called a normal for a plane if it is orthogonal to every vector in the plane.
is called a normal for a plane if it is orthogonal to every vector in the plane.
For example, the unit vector ![]() is a normal vector for
is a normal vector for ![]() plane.
plane.
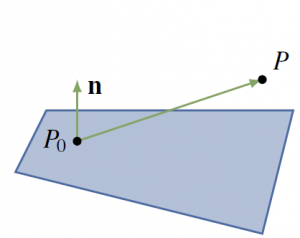
Given a point ![]() and a nonzero vector
and a nonzero vector ![]() , there is a unique plane through
, there is a unique plane through ![]() with normal
with normal ![]() , shaded in Figure 4.2.6. A point
, shaded in Figure 4.2.6. A point ![]() lies on this plane if and only if the vector
lies on this plane if and only if the vector ![]() is orthogonal to
is orthogonal to ![]() —that is, if and only if
—that is, if and only if ![]() . Because
. Because ![Rendered by QuickLaTeX.com \vec{P_{0}P} = \left[ \begin{array}{c} x - x_{0}\\ y - y_{0}\\ z - z_{0} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-040991c9a930deb0cdd53f9c03415336_l3.png) this gives the following result:
this gives the following result:
Scalar equation of a plane
The plane through ![]() with normal
with normal ![Rendered by QuickLaTeX.com \vec{n} = \left[ \begin{array}{c} a\\ b\\ c \end{array} \right] \neq \vec{0}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-e540d456bec740c05b4756a0ab40cd78_l3.png)
as a normal vector is given by
![]()
In other words, a point ![]() is on this plane if and only if
is on this plane if and only if ![]() ,
, ![]() , and
, and ![]() satisfy this equation.
satisfy this equation.
Example 4.2.8
Find an equation of the plane through ![]() with
with ![Rendered by QuickLaTeX.com \vec{n} = \left[ \begin{array}{r} 3\\ -1\\ 2 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c31b123472f9ceb8db8d5c77336438fd_l3.png)
as normal.
Solution:
Here the general scalar equation becomes
![]()
This simplifies to ![]() .
.
If we write ![]() , the scalar equation shows that every plane with normal
, the scalar equation shows that every plane with normal ![Rendered by QuickLaTeX.com \vec{n} = \left[ \begin{array}{r} a\\ b\\ c \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-340e85cba46b65e1ad25f1c96d8506b3_l3.png)
has a linear equation of the form
(4.2) ![]()
for some constant ![]() . Conversely, the graph of this equation is a plane with
. Conversely, the graph of this equation is a plane with ![Rendered by QuickLaTeX.com \vec{n} = \left[ \begin{array}{r} a\\ b\\ c \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-340e85cba46b65e1ad25f1c96d8506b3_l3.png) as a normal vector (assuming that
as a normal vector (assuming that ![]() ,
, ![]() , and
, and ![]() are not all zero).
are not all zero).
Example 4.2.9
Find an equation of the plane through ![]() that is parallel to the plane with equation
that is parallel to the plane with equation ![]() .
.
Solution:
The plane with equation ![]() has normal
has normal ![Rendered by QuickLaTeX.com \vec{n} = \left[ \begin{array}{r} 2\\ -3\\ 0 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f020d7732719774ab8206fbfc6258558_l3.png) . Because the two planes are parallel,
. Because the two planes are parallel, ![]() serves as a normal for the plane we seek, so the equation is
serves as a normal for the plane we seek, so the equation is ![]() for some
for some ![]() according to (4.2). Insisting that
according to (4.2). Insisting that ![]() lies on the plane determines
lies on the plane determines ![]() ; that is,
; that is, ![]() . Hence, the equation is
. Hence, the equation is ![]() .
.
Consider points ![]() and
and ![]() with vectors
with vectors ![Rendered by QuickLaTeX.com \vec{p}_{0} = \left[ \begin{array}{r} x_{0}\\ y_{0}\\ z_{0} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-3e5c0f59df06ae7ce9eb83f8ca01bd2e_l3.png)
and
![Rendered by QuickLaTeX.com \vec{p}= \left[ \begin{array}{r} x\\ y\\ z \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-e5424f262d9670b35e3c6d66211089ca_l3.png) .
.
Given a nonzero vector ![]() , the scalar equation of the plane through
, the scalar equation of the plane through ![]() with normal
with normal ![Rendered by QuickLaTeX.com \vec{n} = \left[ \begin{array}{r} a\\ b\\ c \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-340e85cba46b65e1ad25f1c96d8506b3_l3.png) takes the vector form:
takes the vector form:
Vector Equation of a Plane
The plane with normal ![]() through the point with vector
through the point with vector ![]() is given by
is given by
![]()
In other words, the point with vector ![]() is on the plane if and only if
is on the plane if and only if ![]() satisfies this condition.
satisfies this condition.
Moreover, Equation (4.2) translates as follows:
Every plane with normal ![]() has vector equation
has vector equation ![]() for some number
for some number ![]() .
.
Example 4.2.10
Find the shortest distance from the point ![]() to the plane with equation
to the plane with equation ![]() . Also find the point
. Also find the point ![]() on this plane closest to
on this plane closest to ![]() .
.
Solution:
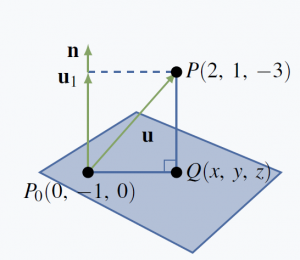 The plane in question has normal
The plane in question has normal ![Rendered by QuickLaTeX.com \vec{n} = \left[ \begin{array}{r} 3\\ -1\\ 4 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-9eddd17b93bab1d235644038f04f8744_l3.png) . Choose any point
. Choose any point ![]() on the plane—say
on the plane—say ![]() —and let
—and let ![]() be the point on the plane closest to
be the point on the plane closest to ![]() (see the diagram). The vector from
(see the diagram). The vector from ![]() to
to ![]() is
is ![Rendered by QuickLaTeX.com \vec{u} = \left[ \begin{array}{r} 2\\ 2\\ -3 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-35fb49d4e5f82dbbb7e07c7de46efa13_l3.png) . Now erect
. Now erect ![]() with its tail at
with its tail at ![]() . Then
. Then ![]() and
and ![]() is the projection of
is the projection of ![]() on
on ![]() :
:
![Rendered by QuickLaTeX.com \begin{equation*} \vec{u}_{1} = \frac{\vec{n} \cdot \vec{u}}{|| \vect{n} ||^2}\vec{n} = \frac{-8}{26} \left[ \begin{array}{r} 3\\ -1 \\ 4 \end{array} \right] = \frac{-4}{13} \left[ \begin{array}{r} 3\\ -1 \\ 4 \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-9aa0e384b6ac6a0869df3536cb19614e_l3.png)
Hence the distance is ![]() . To calculate the point
. To calculate the point ![]() , let
, let ![Rendered by QuickLaTeX.com \vec{q} = \left[ \begin{array}{r} x\\ y \\ z \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-416977fffd2455e19a6748c0b6c8ed8a_l3.png)
and
![Rendered by QuickLaTeX.com \vec{p}_{0} = \left[ \begin{array}{r} 0\\ -1 \\ 0 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-3ac66f3bc93a4bac9339ea0ff5e49023_l3.png)
be the vectors of ![]() and
and ![]() . Then
. Then
![Rendered by QuickLaTeX.com \begin{equation*} \vec{q} = \vec{p}_{0} + \vec{u} - \vec{u}_{1} = \left[ \begin{array}{r} 0\\ -1 \\ 0 \end{array} \right] + \left[ \begin{array}{r} 2\\ 2 \\ -3 \end{array} \right] + \frac{4}{13} \left[ \begin{array}{r} 3\\ -1 \\ 4 \end{array} \right] = \left[ \def\arraystretch{1.5} \begin{array}{r} \frac{38}{13}\\ \frac{9}{13}\\ \frac{-23}{13} \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5ed3cb7c5cbb20c5768fbebb04639a1c_l3.png)
This gives the coordinates of ![]() .
.
The Cross Product
If ![]() ,
, ![]() , and
, and ![]() are three distinct points in
are three distinct points in ![]() that are not all on some line, it is clear geometrically that there is a unique plane containing all three. The vectors
that are not all on some line, it is clear geometrically that there is a unique plane containing all three. The vectors ![]() and
and ![]() both lie in this plane, so finding a normal amounts to finding a nonzero vector orthogonal to both
both lie in this plane, so finding a normal amounts to finding a nonzero vector orthogonal to both ![]() and
and ![]() . The cross product provides a systematic way to do this.
. The cross product provides a systematic way to do this.
Definition 4.8 Cross Product
Given vectors ![Rendered by QuickLaTeX.com \vec{v}_{1}= \left[ \begin{array}{c} x_{1}\\ y_{1} \\ z_{1} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-7c902e8ce90cec9925616cca68a10db5_l3.png) and
and ![Rendered by QuickLaTeX.com \vec{v}_{2}= \left[ \begin{array}{c} x_{2}\\ y_{2} \\ z_{2} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-0d49b1281bfe537b3ad0d7549ed2cd6a_l3.png) , define the cross product
, define the cross product ![]() by
by
![Rendered by QuickLaTeX.com \begin{equation*} \vec{v}_{1} \times \vec{v}_{2} = \left[ \begin{array}{c} y_{1}z_{2} - z_{1}y_{2}\\ -(x_{1}z_{2} - z_{1}x_{2}) \\ x_{1}y_{2} - y_{1}x_{2} \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-55cbd31ea43058baf071509d0a2c06fc_l3.png)
Because it is a vector, ![]() is often called the vector product. There is an easy way to remember this definition using the coordinate vectors:
is often called the vector product. There is an easy way to remember this definition using the coordinate vectors:
![Rendered by QuickLaTeX.com \begin{equation*} \vec{i}= \left[ \begin{array}{c} 1\\ 0 \\ 0 \end{array} \right], \ \vec{j}= \left[ \begin{array}{c} 0\\ 1 \\ 0 \end{array} \right], \mbox{ and } \vec{k}= \left[ \begin{array}{c} 0\\ 0 \\ 1 \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-43da99f15cba2c717daf5a63ae84072f_l3.png)
They are vectors of length ![]() pointing along the positive
pointing along the positive ![]() ,
, ![]() , and
, and ![]() axes. The reason for the name is that any vector can be written as
axes. The reason for the name is that any vector can be written as
![Rendered by QuickLaTeX.com \begin{equation*} \left[ \begin{array}{c} x\\ y \\ z \end{array} \right] = x\vec{i} + y\vec{j} + z\vec{k} \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-562d5b6ec1553207d7c2bae68bdf340b_l3.png)
With this, the cross product can be described as follows:
Determinant form of the cross product
If ![Rendered by QuickLaTeX.com \vec{v}_{1}= \left[ \begin{array}{c} x_{1}\\ y_{1}\\ z_{1} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-2f8993b9aa1dc1aeab91d719ff148d81_l3.png) and
and ![Rendered by QuickLaTeX.com \vec{v}_{2}= \left[ \begin{array}{c} x_{2}\\ y_{2}\\ z_{2} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-bbf5e4fa3e8df005d69981fa2344cfcc_l3.png) are two vectors, then
are two vectors, then
![Rendered by QuickLaTeX.com \begin{equation*} \vec{v}_{1} \times \vec{v}_{2} = \func{det}\left[ \begin{array}{ccc} \vec{i} & x_{1} & x_{2}\\ \vec{j} & y_{1} & y_{2}\\ \vec{k} & z_{1} & z_{2} \end{array} \right] = \left| \begin{array}{cc} y_{1} & y_{2}\\ z_{1} & z_{2} \end{array} \right|\vec{i} - \left| \begin{array}{cc} x_{1} & x_{2}\\ z_{1} & z_{2} \end{array} \right|\vec{j} + \left| \begin{array}{cc} x_{1} & x_{2}\\ y_{1} & y_{2} \end{array} \right|\vec{k} \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-e117dce40f76b9e51673ecae7bcf2307_l3.png)
where the determinant is expanded along the first column.
Example 4.2.11
If ![Rendered by QuickLaTeX.com \vec{v} = \left[\begin{array}{r} 2\\ -1\\ 4 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5343e20725026e1fd7257c50a6f8e102_l3.png) and
and ![Rendered by QuickLaTeX.com \vec{w} = \left[ \begin{array}{r} 1\\ 3\\ 7 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f37d31e9df9e8fa17a9ac370901b27bc_l3.png) , then
, then
![Rendered by QuickLaTeX.com \begin{align*} \vec{v}_{1} \times \vec{v}_{2} = \func{det}\left[ \begin{array}{rrr} \vec{i} & 2 & 1\\ \vec{j} & -1 & 3\\ \vec{k} & 4 & 7 \end{array} \right] &= \left| \begin{array}{rr} -1 & 3\\ 4 & 7 \end{array} \right|\vec{i} - \left| \begin{array}{rr} 2 & 1\\ 4 & 7 \end{array} \right|\vec{j} + \left| \begin{array}{rr} 2 & 1\\ -1 & 3 \end{array} \right|\vec{k}\\ &= -19\vec{i} - 10\vec{j} + 7\vec{k}\\ &= \left[ \begin{array}{r} -19\\ -10\\ 7 \end{array} \right] \end{align*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-8e31c47f51f46ae03406ab3f17f7d4c4_l3.png)
Observe that ![]() is orthogonal to both
is orthogonal to both ![]() and
and ![]() in Example 4.2.11. This holds in general as can be verified directly by computing
in Example 4.2.11. This holds in general as can be verified directly by computing ![]() and
and ![]() , and is recorded as the first part of the following theorem. It will follow from a more general result which, together with the second part, will be proved later on.
, and is recorded as the first part of the following theorem. It will follow from a more general result which, together with the second part, will be proved later on.
Theorem 4.2.5
Let ![]() and
and ![]() be vectors in
be vectors in ![]() :
:
-
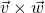 is a vector orthogonal to both
is a vector orthogonal to both  and
and 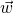 .
. - If
 and
and 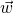 are nonzero, then
are nonzero, then 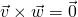 if and only if
if and only if  and
and 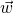 are parallel.
are parallel.
Recall that
![]()
Example 4.2.12
Find the equation of the plane through ![]() ,
, ![]() , and
, and ![]() .
.
Solution:
The vectors
![Rendered by QuickLaTeX.com \vec{PQ} = \left[ \begin{array}{r} 0\\ -2\\ 7 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-6d06f2d1f1cf9806d0ce605884209f40_l3.png) and
and
![Rendered by QuickLaTeX.com \vec{PR} = \left[ \begin{array}{r} 1\\ -5\\ 5 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f4f3dd735febacf08b252b8b9e42ecc1_l3.png)
lie in the plane, so
![Rendered by QuickLaTeX.com \begin{equation*} \vec{PQ} \times \vec{PR} = \func{det}\left[ \begin{array}{rrr} \vec{i} & 0 & 1\\ \vec{j} & -2 & -5\\ \vec{k} & 7 & 5 \end{array} \right] = 25\vec{i} + 7\vec{j} + 2\vec{k} = \left[ \begin{array}{r} 25\\ 7\\ 2 \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-aaebe182733c207c885310327b82ef96_l3.png)
is a normal for the plane (being orthogonal to both ![]() and
and ![]() ). Hence the plane has equation
). Hence the plane has equation
![]()
Since ![]() lies in the plane we have
lies in the plane we have ![]() . Hence
. Hence ![]() and the equation is
and the equation is ![]() . Can you verify that he same equation can be obtained if
. Can you verify that he same equation can be obtained if ![]() and
and ![]() , or
, or ![]() and
and ![]() , are used as the vectors in the plane?
, are used as the vectors in the plane?
4.3 More on the Cross Product
The cross product ![]() of two
of two ![]() -vectors
-vectors ![Rendered by QuickLaTeX.com \vec{v} = \left[ \begin{array}{r} x_{1}\\ y_{1}\\ z_{1} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-aba89974bfa832c355ecbdb7ca96ce3d_l3.png) and
and ![Rendered by QuickLaTeX.com \vec{w} = \left[ \begin{array}{r} x_{2}\\ y_{2}\\ z_{2} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-03692684f1fdba39d5a7fc3eac6615bc_l3.png)
was defined in Section 4.2 where we observed that it can be best remembered using a determinant:
(4.3) ![Rendered by QuickLaTeX.com \begin{equation*} \vec{v} \times \vec{w} = \func{det}\left[ \begin{array}{rrr} \vec{i} & x_{1} & x_{2}\\ \vec{j} & y_{1} & y_{2}\\ \vec{k} & z_{1} & z_{2} \end{array} \right] = \left| \begin{array}{rr} y_{1} & y_{2}\\ z_{1} & z_{2} \end{array} \right|\vec{i} - \left| \begin{array}{rr} x_{1} & x_{2}\\ z_{1} & z_{2} \end{array} \right|\vec{j} + \left| \begin{array}{rr} x_{1} & x_{2}\\ y_{1} & y_{2} \end{array} \right|\vec{k} \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-ea3d35222d771b214950ef4281ef5970_l3.png)
Here ![Rendered by QuickLaTeX.com \vec{i} = \left[ \begin{array}{r} 1\\ 0\\ 0 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-7111705b2033034e3e1fa0232eff5927_l3.png) ,
, ![Rendered by QuickLaTeX.com \vec{j} = \left[ \begin{array}{r} 0\\ 1\\ 0 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-76f67acf423ee85d4aa36739e8c079e6_l3.png) , and
, and
![Rendered by QuickLaTeX.com \vec{k} = \left[ \begin{array}{r} 1\\ 0\\ 0 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f866c80a5a41dd6ab29a78b70df5e8b4_l3.png) are the coordinate vectors, and the determinant is expanded along the first column. We observed (but did not prove) in Theorem 4.2.5 that
are the coordinate vectors, and the determinant is expanded along the first column. We observed (but did not prove) in Theorem 4.2.5 that ![]() is orthogonal to both
is orthogonal to both ![]() and
and ![]() . This follows easily from the next result.
. This follows easily from the next result.
Theorem 4.3.1
If ![Rendered by QuickLaTeX.com \vec{u} = \left[ \begin{array}{r} x_{0}\\ y_{0}\\ z_{0} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-df0710484294f5bdd7ae4e77d6e9e6e3_l3.png) ,
, ![Rendered by QuickLaTeX.com \vec{v} = \left[ \begin{array}{r} x_{1}\\ y_{1}\\ z_{1} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-0357f79dd32c5ed062a0624eb9cd9c7a_l3.png) , and
, and ![Rendered by QuickLaTeX.com \vec{w} = \left[ \begin{array}{r} x_{2}\\ y_{2}\\ z_{2} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-ab8ecae6db0faff88cc522b34ee67c1c_l3.png) , then
, then ![Rendered by QuickLaTeX.com \vec{u} \cdot (\vec{v} \times \vec{w}) = \func{det}\left[ \begin{array}{rrr} x_{0} & x_{1} & x_{2}\\ y_{0} & y_{1} & y_{2}\\ z_{0} & z_{1} & z_{2} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-65f52c4c316b1d006eb9dcf8e8de2bd8_l3.png) .
.
Proof:
Recall that ![]() is computed by multiplying corresponding components of
is computed by multiplying corresponding components of ![]() and
and ![]() and then adding. Using equation (4.3), the result is:
and then adding. Using equation (4.3), the result is:
![Rendered by QuickLaTeX.com \begin{equation*} \vec{u} \cdot (\vec{v} \times \vec{w}) = x_{0}\left(\left| \begin{array}{rr} y_{1} & y_{2}\\ z_{1} & z_{2} \end{array} \right|\right) + y_{0}\left(- \left| \begin{array}{rr} x_{1} & x_{2}\\ z_{1} & z_{2} \end{array} \right|\right) +z_{0}\left( \left| \begin{array}{rr} x_{1} & x_{2}\\ y_{1} & y_{2} \end{array} \right|\right) = \func{det}\left[ \begin{array}{rrr} x_{0} & x_{1} & x_{2}\\ y_{0} & y_{1} & y_{2}\\ z_{0} & z_{1} & z_{2} \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d5ae86d2f124a0e6c79af7368c64413f_l3.png)
where the last determinant is expanded along column 1.
The result in Theorem 4.3.1 can be succinctly stated as follows: If ![]() ,
, ![]() , and
, and ![]() are three vectors in
are three vectors in ![]() , then
, then
![]()
where ![]() denotes the matrix with
denotes the matrix with ![]() ,
, ![]() , and
, and ![]() as its columns. Now it is clear that
as its columns. Now it is clear that ![]() is orthogonal to both
is orthogonal to both ![]() and
and ![]() because the determinant of a matrix is zero if two columns are identical.
because the determinant of a matrix is zero if two columns are identical.
Because of (4.3) and Theorem 4.3.1, several of the following properties of the cross product follow from
properties of determinants (they can also be verified directly).
Theorem 4.3.2
Let ![]() ,
, ![]() , and
, and ![]() denote arbitrary vectors in
denote arbitrary vectors in ![]() .
.
-
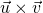 is a vector.
is a vector. -
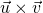 is orthogonal to both
is orthogonal to both 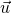 and
and  .
.  .
. .
.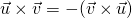 .
.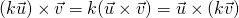 for any scalar
for any scalar 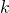 .
.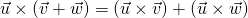 .
.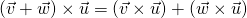 .
.
We have seen some of these results in the past; can you prove 6,7, and 8?
We now come to a fundamental relationship between the dot and cross products.
Theorem 4.3.3 Lagrange Identity
If ![]() and
and ![]() are any two vectors in
are any two vectors in ![]() , then
, then
![]()
Proof:
Given ![]() and
and ![]() , introduce a coordinate system and write
, introduce a coordinate system and write
![Rendered by QuickLaTeX.com \vec{u} = \left[ \begin{array}{r} x_{1}\\ y_{1}\\ z_{1} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-ac1c58f774f736f8ba6c30777994943c_l3.png) and
and
![Rendered by QuickLaTeX.com \vec{v} = \left[ \begin{array}{r} x_{2}\\ y_{2}\\ z_{2} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-dfbdba58336fb58b95ccc8e04cbe20d8_l3.png) in component form. Then all the terms in the identity can be computed in terms of the components.
in component form. Then all the terms in the identity can be computed in terms of the components.
An expression for the magnitude of the vector ![]() can be easily obtained from the Lagrange identity. If
can be easily obtained from the Lagrange identity. If ![]() is the angle between
is the angle between ![]() and
and ![]() , substituting
, substituting ![]() into the Lagrange identity gives
into the Lagrange identity gives
![]()
using the fact that ![]() . But
. But ![]() is nonnegative on the range
is nonnegative on the range ![]() , so taking the positive square root of both sides gives
, so taking the positive square root of both sides gives
![]()

This expression for ![]() makes no reference to a coordinate system and, moreover, it has a nice geometrical interpretation. The parallelogram determined by the vectors
makes no reference to a coordinate system and, moreover, it has a nice geometrical interpretation. The parallelogram determined by the vectors ![]() and
and ![]() has base length
has base length ![]() and altitude
and altitude ![]() . Hence the area of the parallelogram formed by
. Hence the area of the parallelogram formed by ![]() and
and ![]() is
is
![]()
Theorem 4.3.4
If ![]() and
and ![]() are two nonzero vectors and
are two nonzero vectors and ![]() is the angle between
is the angle between ![]() and
and ![]() , then:
, then:
-
 the area of the parallelogram determined by
the area of the parallelogram determined by 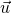 and
and  .
. 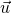 and
and  are parallel if and only if
are parallel if and only if 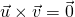 .
.
Proof of 2:
By (1), ![]() if and only if the area of the parallelogram is zero. The area vanishes if and only if
if and only if the area of the parallelogram is zero. The area vanishes if and only if ![]() and
and ![]() have the same or opposite direction—that is, if and only if they are parallel.
have the same or opposite direction—that is, if and only if they are parallel.
Example 4.3.1
Find the area of the triangle with vertices ![]() ,
, ![]() , and
, and ![]() .
.
Solution:
We have
![Rendered by QuickLaTeX.com \vec{RP} = \left[ \begin{array}{r} 1\\ 1\\ -1 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-8e0f99a9ac49165517e8788da7002a04_l3.png) and
and ![Rendered by QuickLaTeX.com \vec{RQ} = \left[ \begin{array}{r} 2\\ -1\\ 0 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-85bba21038b87b1ab05a3b0fb228a137_l3.png) . The area of the triangle is half the area of the parallelogram formed by these vectors, and so equals
. The area of the triangle is half the area of the parallelogram formed by these vectors, and so equals ![]() . We have
. We have
![Rendered by QuickLaTeX.com \begin{equation*} \vec{RP} \times \vec{RQ} = \func{det}\left[ \begin{array}{rrr} \vect{i} & 1 & 2\\ \vect{j} & 1 & -1\\ \vect{k} & -1 & 0 \end{array} \right] = \left[ \begin{array}{r} -1\\ -2\\ -3 \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-eb3aa9ea2f18cf128fd3f57759e13e88_l3.png)
so the area of the triangle is ![]()

If three vectors ![]() ,
, ![]() , and
, and ![]() are given, they determine a “squashed” rectangular solid called a parallelepiped (Figure 4.3.2), and it is often useful to be able to find the volume of such a solid. The base of the solid is the parallelogram determined by
are given, they determine a “squashed” rectangular solid called a parallelepiped (Figure 4.3.2), and it is often useful to be able to find the volume of such a solid. The base of the solid is the parallelogram determined by ![]() and
and ![]() , so it has area
, so it has area ![]() . The height of the solid is the length
. The height of the solid is the length ![]() of the projection of
of the projection of ![]() on
on ![]() . Hence
. Hence
![]()
Thus the volume of the parallelepiped is ![]() . This proves
. This proves
Theorem 4.3.5
The volume of the parallelepiped determined by three vectors ![]() ,
, ![]() , and
, and ![]() is given by
is given by ![]() .
.
Example 4.3.2
Find the volume of the parallelepiped determined by the vectors
![Rendered by QuickLaTeX.com \begin{equation*} \vec{w} = \left[ \begin{array}{r} 1\\ 2\\ -1 \end{array} \right], \vec{u} = \left[ \begin{array}{r} 1\\ 1\\ 0 \end{array} \right], \vec{v} = \left \begin{array}{r} -2\\ 0\\ 1 \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c1a3639375f2f032e95ae837e9db2907_l3.png)
Solution:
By Theorem 4.3.1, ![Rendered by QuickLaTeX.com \vec{w} \cdot (\vec{u} \times \vec{v}) = \func{det}\left[ \begin{array}{rrr} 1 & 1 & -2\\ 2 & 1 & 0\\ -1 & 0 & 1 \end{array} \right] = -3](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-dadaf0056ccc8ff2bd530976887f32ad_l3.png) .
.
Hence the volume is ![]() by Theorem 4.3.5.
by Theorem 4.3.5.
We can now give an intrinsic description of the cross product ![]() .
.
Right-hand Rule
If the vector ![]() is grasped in the right hand and the fingers curl around from
is grasped in the right hand and the fingers curl around from ![]() to
to ![]() through the angle
through the angle ![]() , the thumb points in the direction for
, the thumb points in the direction for ![]()
To indicate why this is true, introduce coordinates in ![]() as follows: Let
as follows: Let ![]() and
and ![]() have a common tail
have a common tail ![]() , choose the origin at
, choose the origin at ![]() , choose the
, choose the ![]() axis so that
axis so that ![]() points in the positive
points in the positive ![]() direction, and then choose the
direction, and then choose the ![]() axis so that
axis so that ![]() is in the
is in the ![]() –
–![]() plane and the positive
plane and the positive ![]() axis is on the same side of the
axis is on the same side of the ![]() axis as
axis as ![]() . Then, in this system,
. Then, in this system, ![]() and
and ![]() have component form
have component form
![Rendered by QuickLaTeX.com \vec{u} = \left[ \begin{array}{r} a\\ 0\\ 0 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-8ec49bb62b33a46db460e74dd3641a3e_l3.png) and
and ![Rendered by QuickLaTeX.com \vec{v} = \left[ \begin{array}{r} b\\ c\\ 0 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-3efc17fe8f791104d26f5254e5220c2f_l3.png)
where ![]() and
and ![]() . Can you draw a graph based on the description here?
. Can you draw a graph based on the description here?
The right-hand rule asserts that ![]() should point in the positive
should point in the positive ![]() direction. But our definition of
direction. But our definition of ![]() gives
gives
![Rendered by QuickLaTeX.com \begin{equation*} \vec{u} \times \vec{v} = \func{det}\left[ \begin{array}{rrr} \vect{i} & a & b\\ \vect{j} & 0 & c\\ \vect{k} & 0 & 0 \end{array} \right] = \left[ \begin{array}{c} 0\\ 0\\ ac \end{array} \right] = (ac)\vect{k} \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-42229c22e002c59e3837ddce0fc126dd_l3.png)
and ![]() has the positive
has the positive ![]() direction because
direction because ![]() .
.

