2 Matrix Algebra
Introduction
In the study of systems of linear equations in Chapter 1, we found it convenient to manipulate the augmented matrix of the system. Our aim was to reduce it to row-echelon form (using elementary row operations) and hence to write down all solutions to the system. In the present chapter we consider matrices for their own sake. While some of the motivation comes from linear equations, it turns out that matrices can be multiplied and added and so form an algebraic system somewhat analogous to the real numbers. This “matrix algebra” is useful in ways that are quite different from the study of linear equations. For example, the geometrical transformations obtained by rotating the euclidean plane about the origin can be viewed as multiplications by certain ![]() matrices. These “matrix transformations” are an important tool in geometry and, in turn, the geometry provides a “picture” of the matrices. Furthermore, matrix algebra has many other applications, some of which will be explored in this chapter. This subject is quite old and was first studied systematically in 1858 by Arthur Cayley.
matrices. These “matrix transformations” are an important tool in geometry and, in turn, the geometry provides a “picture” of the matrices. Furthermore, matrix algebra has many other applications, some of which will be explored in this chapter. This subject is quite old and was first studied systematically in 1858 by Arthur Cayley.
2.1 Matrix Addition, Scalar Multiplication, and Transposition
A rectangular array of numbers is called a matrix (the plural is matrices), and the numbers are called the entries of the matrix. Matrices are usually denoted by uppercase letters: ![]() ,
, ![]() ,
, ![]() , and so on. Hence,
, and so on. Hence,
![Rendered by QuickLaTeX.com \begin{equation*} A = \left[ \begin{array}{rrr} 1 & 2 & -1 \\ 0 & 5 & 6 \end{array} \right] \quad B = \left[ \begin{array}{rr} 1 & -1 \\ 0 & 2 \end{array} \right] \quad C = \left[ \begin{array}{r} 1 \\ 3 \\ 2 \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-fcd4005cd6628968209b06c26113a40f_l3.png)
are matrices. Clearly matrices come in various shapes depending on the number of rows and columns. For example, the matrix ![]() shown has
shown has ![]() rows and
rows and ![]() columns. In general, a matrix with
columns. In general, a matrix with ![]() rows and
rows and ![]() columns is referred to as an
columns is referred to as an ![]() matrix or as having size
matrix or as having size ![]() . Thus matrices
. Thus matrices ![]() ,
, ![]() , and
, and ![]() above have sizes
above have sizes ![]() ,
, ![]() , and
, and ![]() , respectively. A matrix of size
, respectively. A matrix of size ![]() is called a row matrix, whereas one of size
is called a row matrix, whereas one of size ![]() is called a column matrix. Matrices of size
is called a column matrix. Matrices of size ![]() for some
for some ![]() are called square matrices.
are called square matrices.
Each entry of a matrix is identified by the row and column in which it lies. The rows are numbered from the top down, and the columns are numbered from left to right. Then the ![]() -entry of a matrix is the number lying simultaneously in row
-entry of a matrix is the number lying simultaneously in row ![]() and column
and column ![]() . For example,
. For example,
![Rendered by QuickLaTeX.com \begin{align*} \mbox{The } (1, 2) \mbox{-entry of } &\left[ \begin{array}{rr} 1 & -1 \\ 0 & 1 \end{array}\right] \mbox{ is } -1. \\ \mbox{The } (2, 3) \mbox{-entry of } &\left[ \begin{array}{rrr} 1 & 2 & -1 \\ 0 & 5 & 6 \end{array}\right] \mbox{ is } 6. \end{align*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-14e3d57d5a305ed2eba3f18ceca28ae3_l3.png)
A special notation is commonly used for the entries of a matrix. If ![]() is an
is an ![]() matrix, and if the
matrix, and if the ![]() -entry of
-entry of ![]() is denoted as
is denoted as ![]() , then
, then ![]() is displayed as follows:
is displayed as follows:
![Rendered by QuickLaTeX.com \begin{equation*} A = \left[ \begin{array}{ccccc} a_{11} & a_{12} & a_{13} & \cdots & a_{1n} \\ a_{21} & a_{22} & a_{23} & \cdots & a_{2n} \\ \vdots & \vdots & \vdots & & \vdots \\ a_{m1} & a_{m2} & a_{m3} & \cdots & a_{mn} \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-60548ab398daa026e03f00f588da6d67_l3.png)
This is usually denoted simply as ![]() . Thus
. Thus ![]() is the entry in row
is the entry in row ![]() and column
and column ![]() of
of ![]() . For example, a
. For example, a ![]() matrix in this notation is written
matrix in this notation is written
![Rendered by QuickLaTeX.com \begin{equation*} A = \left[ \begin{array}{cccc} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-b5e4fcf887d32ad59d0af79bbc22c735_l3.png)
It is worth pointing out a convention regarding rows and columns: Rows are mentioned before columns. For example:
- If a matrix has size
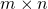 , it has
, it has 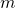 rows and
rows and 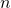 columns.
columns. - If we speak of the
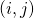 -entry of a matrix, it lies in row
-entry of a matrix, it lies in row 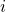 and column
and column 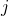 .
. - If an entry is denoted
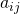 , the first subscript
, the first subscript 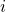 refers to the row and the second subscript
refers to the row and the second subscript 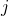 to the column in which
to the column in which 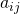 lies.
lies.
Two points ![]() and
and ![]() in the plane are equal if and only if they have the same coordinates, that is
in the plane are equal if and only if they have the same coordinates, that is ![]() and
and ![]() . Similarly, two matrices
. Similarly, two matrices ![]() and
and ![]() are called equal (written
are called equal (written ![]() ) if and only if:
) if and only if:
- They have the same size.
- Corresponding entries are equal.
If the entries of ![]() and
and ![]() are written in the form
are written in the form ![]() ,
, ![]() , described earlier, then the second condition takes the following form:
, described earlier, then the second condition takes the following form:
![]()
Example 2.1.1
discuss the possibility that
Solution:
![]() is impossible because
is impossible because ![]() and
and ![]() are of different sizes:
are of different sizes: ![]() is
is ![]() whereas
whereas ![]() is
is ![]() . Similarly,
. Similarly, ![]() is impossible. But
is impossible. But ![]() is possible provided that corresponding entries are equal:
is possible provided that corresponding entries are equal:
![]()
means ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
Matrix Addition
Definition 2.1 Matrix Addition
If ![]() and
and ![]() , this takes the form
, this takes the form
![]()
Note that addition is not defined for matrices of different sizes.
Example 2.1.2
and
compute
Solution:
![]()
Example 2.1.3
Solution:
Add the matrices on the left side to obtain
![]()
Because corresponding entries must be equal, this gives three equations: ![]() ,
, ![]() , and
, and ![]() . Solving these yields
. Solving these yields ![]() ,
, ![]() ,
, ![]() .
.
If ![]() ,
, ![]() , and
, and ![]() are any matrices of the same size, then
are any matrices of the same size, then
(commutative law) ![]()
In fact, if ![]() and
and ![]() , then the
, then the ![]() -entries of
-entries of ![]() and
and ![]() are, respectively,
are, respectively, ![]() and
and ![]() . Since these are equal for all
. Since these are equal for all ![]() and
and ![]() , we get
, we get
![]()
The associative law is verified similarly.
The ![]() matrix in which every entry is zero is called the
matrix in which every entry is zero is called the ![]() zero matrix and is denoted as
zero matrix and is denoted as ![]() (or
(or ![]() if it is important to emphasize the size). Hence,
if it is important to emphasize the size). Hence,
![]()
holds for all ![]() matrices
matrices ![]() . The negative of an
. The negative of an ![]() matrix
matrix ![]() (written
(written ![]() ) is defined to be the
) is defined to be the ![]() matrix obtained by multiplying each entry of
matrix obtained by multiplying each entry of ![]() by
by ![]() . If
. If ![]() , this becomes
, this becomes ![]() . Hence,
. Hence,
![]()
holds for all matrices ![]() where, of course,
where, of course, ![]() is the zero matrix of the same size as
is the zero matrix of the same size as ![]() .
.
A closely related notion is that of subtracting matrices. If ![]() and
and ![]() are two
are two ![]() matrices, their difference
matrices, their difference ![]() is defined by
is defined by
![]()
Note that if ![]() and
and ![]() , then
, then
![]()
is the ![]() matrix formed by subtracting corresponding entries.
matrix formed by subtracting corresponding entries.
Example 2.1.4
Solution:
![Rendered by QuickLaTeX.com \begin{align*} -A &= \left[ \begin{array}{rrr} -3 & 1 & 0 \\ -1 & -2 & 4 \end{array} \right] \\ A - B &= \left[ \begin{array}{lcr} 3 - 1 & -1 - (-1) & 0 - 1 \\ 1 - (-2) & 2 - 0 & -4 - 6 \end{array} \right] = \left[ \begin{array}{rrr} 2 & 0 & -1 \\ 3 & 2 & -10 \end{array} \right] \\ A + B - C &= \left[ \begin{array}{rrl} 3 + 1 - 1 & -1 - 1 - 0 & 0 + 1 -(-2) \\ 1 - 2 - 3 & 2 + 0 - 1 & -4 + 6 -1 \end{array} \right] = \left[ \begin{array}{rrr} 3 & -2 & 3 \\ -4 & 1 & 1 \end{array} \right] \end{align*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-8297271fe9f34109b21556ca55de37db_l3.png)
Example 2.1.5
where
We solve a numerical equation ![]() by subtracting the number
by subtracting the number ![]() from both sides to obtain
from both sides to obtain ![]() . This also works for matrices. To solve
. This also works for matrices. To solve
![]()
simply subtract the matrix
![]()
from both sides to get
![]()
The reader should verify that this matrix ![]() does indeed satisfy the original equation.
does indeed satisfy the original equation.
The solution in Example 2.1.5 solves the single matrix equation ![]() directly via matrix subtraction:
directly via matrix subtraction: ![]() . This ability to work with matrices as entities lies at the heart of matrix algebra.
. This ability to work with matrices as entities lies at the heart of matrix algebra.
It is important to note that the sizes of matrices involved in some calculations are often determined by the context. For example, if
![]()
then ![]() and
and ![]() must be the same size (so that
must be the same size (so that ![]() makes sense), and that size must be
makes sense), and that size must be ![]() (so that the sum is
(so that the sum is ![]() ). For simplicity we shall often omit reference to such facts when they are clear from the context.
). For simplicity we shall often omit reference to such facts when they are clear from the context.
Scalar Multiplication
In gaussian elimination, multiplying a row of a matrix by a number ![]() means multiplying every entry of that row by
means multiplying every entry of that row by ![]() .
.
Definition 2.2 Matrix Scalar Multiplication
The term scalar arises here because the set of numbers from which the entries are drawn is usually referred to as the set of scalars. We have been using real numbers as scalars, but we could equally well have been using complex numbers.
Example 2.1.6
and
compute
Solution:
![Rendered by QuickLaTeX.com \begin{align*} 5A &= \left[ \begin{array}{rrr} 15 & -5 & 20 \\ 10 & 0 & 30 \end{array} \right], \quad \frac{1}{2}B = \left[ \begin{array}{rrr} \frac{1}{2} & 1 & -\frac{1}{2} \\ 0 & \frac{3}{2} & 1 \end{array} \right] \\ 3A - 2B &= \left[ \begin{array}{rrr} 9 & -3 & 12 \\ 6 & 0 & 18 \end{array} \right] - \left[ \begin{array}{rrr} 2 & 4 & -2 \\ 0 & 6 & 4 \end{array} \right] = \left[ \begin{array}{rrr} 7 & -7 & 14 \\ 6 & -6 & 14 \end{array} \right] \end{align*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-11453525d60950649bb2baad5d426259_l3.png)
If ![]() is any matrix, note that
is any matrix, note that ![]() is the same size as
is the same size as ![]() for all scalars
for all scalars ![]() . We also have
. We also have
![]()
because the zero matrix has every entry zero. In other words, ![]() if either
if either ![]() or
or ![]() . The converse of this statement is also true, as Example 2.1.7 shows.
. The converse of this statement is also true, as Example 2.1.7 shows.
Example 2.1.7
Solution:
Write ![]() so that
so that ![]() means
means ![]() for all
for all ![]() and
and ![]() . If
. If ![]() , there is nothing to do. If
, there is nothing to do. If ![]() , then
, then ![]() implies that
implies that ![]() for all
for all ![]() and
and ![]() ; that is,
; that is, ![]() .
.
For future reference, the basic properties of matrix addition and scalar multiplication are listed in Theorem 2.1.1.
Theorem 2.1.1
Let ![]() ,
, ![]() , and
, and ![]() denote arbitrary
denote arbitrary ![]() matrices where
matrices where ![]() and
and ![]() are fixed. Let
are fixed. Let ![]() and
and ![]() denote arbitrary real numbers. Then
denote arbitrary real numbers. Then
-
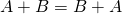 .
.  .
.- There is an
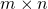 matrix
matrix  , such that
, such that 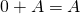 for each
for each  .
. - For each
 there is an
there is an 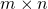 matrix,
matrix,  , such that
, such that 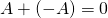 .
. -
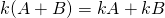 .
. -
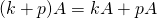 .
. -
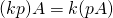 .
. -
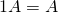 .
.
Proof:
Properties 1–4 were given previously. To check Property 5, let ![]() and
and ![]() denote matrices of the same size. Then
denote matrices of the same size. Then ![]() , as before, so the
, as before, so the ![]() -entry of
-entry of ![]() is
is
![]()
But this is just the ![]() -entry of
-entry of ![]() , and it follows that
, and it follows that ![]() . The other Properties can be similarly verified; the details are left to the reader.
. The other Properties can be similarly verified; the details are left to the reader.
The Properties in Theorem 2.1.1 enable us to do calculations with matrices in much the same way that
numerical calculations are carried out. To begin, Property 2 implies that the sum
![]()
is the same no matter how it is formed and so is written as ![]() . Similarly, the sum
. Similarly, the sum
![]()
is independent of how it is formed; for example, it equals both ![]() and
and ![]() . Furthermore, property 1 ensures that, for example,
. Furthermore, property 1 ensures that, for example,
![]()
In other words, the order in which the matrices are added does not matter. A similar remark applies to sums of five (or more) matrices.
Properties 5 and 6 in Theorem 2.1.1 are called distributive laws for scalar multiplication, and they extend to sums of more than two terms. For example,
![]()
![]()
Similar observations hold for more than three summands. These facts, together with properties 7 and 8, enable us to simplify expressions by collecting like terms, expanding, and taking common factors in exactly the same way that algebraic expressions involving variables and real numbers are manipulated. The following example illustrates these techniques.
Example 2.1.8
Solution:
The reduction proceeds as though ![]() ,
, ![]() , and
, and ![]() were variables.
were variables.
![Rendered by QuickLaTeX.com \begin{align*} 2(A &+ 3C) - 3(2C - B) - 3 \left[ 2(2A + B - 4C) - 4(A - 2C) \right] \\ &= 2A + 6C - 6C + 3B - 3 \left[ 4A + 2B - 8C - 4A + 8C \right] \\ &= 2A + 3B - 3 \left[ 2B \right] \\ &= 2A - 3B \end{align*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-45e5ae1d1480bdaf9f19ecd41ca98e77_l3.png)
Transpose of a Matrix
Many results about a matrix ![]() involve the rows of
involve the rows of ![]() , and the corresponding result for columns is derived in an analogous way, essentially by replacing the word row by the word column throughout. The following definition is made with such applications in mind.
, and the corresponding result for columns is derived in an analogous way, essentially by replacing the word row by the word column throughout. The following definition is made with such applications in mind.
Definition 2.3 Transpose of a Matrix
In other words, the first row of ![]() is the first column of
is the first column of ![]() (that is it consists of the entries of column 1 in order). Similarly the second row of
(that is it consists of the entries of column 1 in order). Similarly the second row of ![]() is the second column of
is the second column of ![]() , and so on.
, and so on.
Example 2.1.9
![Rendered by QuickLaTeX.com \begin{equation*} A = \left[ \begin{array}{r} 1 \\ 3 \\ 2 \end{array} \right] \quad B = \left[ \begin{array}{rrr} 5 & 2 & 6 \end{array} \right] \quad C = \left[ \begin{array}{rr} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{array} \right] \quad D = \left[ \begin{array}{rrr} 3 & 1 & -1 \\ 1 & 3 & 2 \\ -1 & 2 & 1 \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-a0da49245fb2b147f46e2e36c8bc9f81_l3.png)
Solution:
![Rendered by QuickLaTeX.com \begin{equation*} A^{T} = \left[ \begin{array}{rrr} 1 & 3 & 2 \end{array} \right],\ B^{T} = \left[ \begin{array}{r} 5 \\ 2 \\ 6 \end{array} \right],\ C^{T} = \left[ \begin{array}{rrr} 1 & 3 & 5 \\ 2 & 4 & 6 \end{array} \right], \mbox{ and } D^{T} = D. \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-40fd27d13cb810f642d6799c6a294a30_l3.png)
If ![]() is a matrix, write
is a matrix, write ![]() . Then
. Then ![]() is the
is the ![]() th element of the
th element of the ![]() th row of
th row of ![]() and so is the
and so is the ![]() th element of the
th element of the ![]() th column of
th column of ![]() . This means
. This means ![]() , so the definition of
, so the definition of ![]() can be stated as follows:
can be stated as follows:
(2.1) ![]()
This is useful in verifying the following properties of transposition.
Theorem 2.1.2
Let ![]() and
and ![]() denote matrices of the same size, and let
denote matrices of the same size, and let ![]() denote a scalar.
denote a scalar.
- If
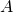 is an
is an 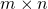 matrix, then
matrix, then 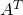 is an
is an 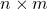 matrix.
matrix. 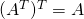 .
.-
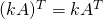 .
. 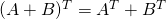 .
.
Proof:
Property 1 is part of the definition of ![]() , and Property 2 follows from (2.1). As to Property 3: If
, and Property 2 follows from (2.1). As to Property 3: If ![]() , then
, then ![]() , so (2.1) gives
, so (2.1) gives
![]()
Finally, if ![]() , then
, then ![]() where
where ![]() Then (2.1) gives Property 4:
Then (2.1) gives Property 4:
![]()
There is another useful way to think of transposition. If ![]() is an
is an ![]() matrix, the elements
matrix, the elements ![]() are called the main diagonal of
are called the main diagonal of ![]() . Hence the main diagonal extends down and to the right from the upper left corner of the matrix
. Hence the main diagonal extends down and to the right from the upper left corner of the matrix ![]() ; it is shaded in the following examples:
; it is shaded in the following examples:
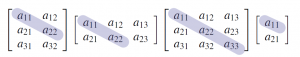
Thus forming the transpose of a matrix ![]() can be viewed as “flipping”
can be viewed as “flipping” ![]() about its main diagonal, or as “rotating”
about its main diagonal, or as “rotating” ![]() through
through ![]() about the line containing the main diagonal. This makes Property 2 in Theorem~?? transparent.
about the line containing the main diagonal. This makes Property 2 in Theorem~?? transparent.
Example 2.1.10
Solution:
Using Theorem 2.1.2, the left side of the equation is
![]()
Hence the equation becomes
![]()
Thus
![]() , so finally
, so finally
![]() .
.
Note that Example 2.1.10 can also be solved by first transposing both sides, then solving for ![]() , and so obtaining
, and so obtaining ![]() . The reader should do this.
. The reader should do this.
The matrix ![]() in Example 2.1.9 has the property that
in Example 2.1.9 has the property that ![]() . Such matrices are important; a matrix
. Such matrices are important; a matrix ![]() is called symmetric if
is called symmetric if ![]() . A symmetric matrix
. A symmetric matrix ![]() is necessarily square (if
is necessarily square (if ![]() is
is ![]() , then
, then ![]() is
is ![]() , so
, so ![]() forces
forces ![]() ). The name comes from the fact that these matrices exhibit a symmetry about the main diagonal. That is, entries that are directly across the main diagonal from each other are equal.
). The name comes from the fact that these matrices exhibit a symmetry about the main diagonal. That is, entries that are directly across the main diagonal from each other are equal.
For example, ![Rendered by QuickLaTeX.com \left[ \begin{array}{ccc} a & b & c \\ b^\prime & d & e \\ c^\prime & e^\prime & f \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c874e4fc13043e1eb1536b3d3b88b25f_l3.png) is symmetric when
is symmetric when ![]() ,
, ![]() , and
, and ![]() .
.
Example 2.1.11
Solution:
We have ![]() and
and ![]() , so, by Theorem 2.1.2, we have
, so, by Theorem 2.1.2, we have ![]() . Hence
. Hence ![]() is symmetric.
is symmetric.
Example 2.1.12
Solution:
If we iterate the given equation, Theorem 2.1.2 gives
![]()
Subtracting ![]() from both sides gives
from both sides gives ![]() , so
, so ![]() .
.
2.2 Matrix-Vector Multiplication
Up to now we have used matrices to solve systems of linear equations by manipulating the rows of the augmented matrix. In this section we introduce a different way of describing linear systems that makes more use of the coefficient matrix of the system and leads to a useful way of “multiplying” matrices.
Vectors
It is a well-known fact in analytic geometry that two points in the plane with coordinates ![]() and
and ![]() are equal if and only if
are equal if and only if ![]() and
and ![]() . Moreover, a similar condition applies to points
. Moreover, a similar condition applies to points ![]() in space. We extend this idea as follows.
in space. We extend this idea as follows.
An ordered sequence ![]() of real numbers is called an ordered
of real numbers is called an ordered ![]() –tuple. The word “ordered” here reflects our insistence that two ordered
–tuple. The word “ordered” here reflects our insistence that two ordered ![]() -tuples are equal if and only if corresponding entries are the same. In other words,
-tuples are equal if and only if corresponding entries are the same. In other words,
![]()
Thus the ordered ![]() -tuples and
-tuples and ![]() -tuples are just the ordered pairs and triples familiar from geometry.
-tuples are just the ordered pairs and triples familiar from geometry.
Definition 2.4 The set ![]() of ordered
of ordered ![]() -tuples of real numbers
-tuples of real numbers
![]()
There are two commonly used ways to denote the ![]() -tuples in
-tuples in ![]() : As rows
: As rows ![]() or columns
or columns ![]() ;
;
the notation we use depends on the context. In any event they are called vectors or ![]() –vectors and will be denoted using bold type such as x or v. For example, an
–vectors and will be denoted using bold type such as x or v. For example, an ![]() matrix
matrix ![]() will be written as a row of columns:
will be written as a row of columns:
![]()
If ![]() and
and ![]() are two
are two ![]() -vectors in
-vectors in ![]() , it is clear that their matrix sum
, it is clear that their matrix sum ![]() is also in
is also in ![]() as is the scalar multiple
as is the scalar multiple ![]() for any real number
for any real number ![]() . We express this observation by saying that
. We express this observation by saying that ![]() is closed under addition and scalar multiplication. In particular, all the basic properties in Theorem 2.1.1 are true of these
is closed under addition and scalar multiplication. In particular, all the basic properties in Theorem 2.1.1 are true of these ![]() -vectors. These properties are fundamental and will be used frequently below without comment. As for matrices in general, the
-vectors. These properties are fundamental and will be used frequently below without comment. As for matrices in general, the ![]() zero matrix is called the zero
zero matrix is called the zero ![]() –vector in
–vector in ![]() and, if
and, if ![]() is an
is an ![]() -vector, the
-vector, the ![]() -vector
-vector ![]() is called the negative
is called the negative ![]() .
.
Of course, we have already encountered these ![]() -vectors in Section 1.3 as the solutions to systems of linear equations with
-vectors in Section 1.3 as the solutions to systems of linear equations with ![]() variables. In particular we defined the notion of a linear combination of vectors and showed that a linear combination of solutions to a homogeneous system is again a solution. Clearly, a linear combination of
variables. In particular we defined the notion of a linear combination of vectors and showed that a linear combination of solutions to a homogeneous system is again a solution. Clearly, a linear combination of ![]() -vectors in
-vectors in ![]() is again in
is again in ![]() , a fact that we will be using.
, a fact that we will be using.
Matrix-Vector Multiplication
Given a system of linear equations, the left sides of the equations depend only on the coefficient matrix ![]() and the column
and the column ![]() of variables, and not on the constants. This observation leads to a fundamental idea in linear algebra: We view the left sides of the equations as the “product”
of variables, and not on the constants. This observation leads to a fundamental idea in linear algebra: We view the left sides of the equations as the “product” ![]() of the matrix
of the matrix ![]() and the vector
and the vector ![]() . This simple change of perspective leads to a completely new way of viewing linear systems—one that is very useful and will occupy our attention throughout this book.
. This simple change of perspective leads to a completely new way of viewing linear systems—one that is very useful and will occupy our attention throughout this book.
To motivate the definition of the “product” ![]() , consider first the following system of two equations in three variables:
, consider first the following system of two equations in three variables:
(2.2) ![]()
and let ![]() ,
, ![Rendered by QuickLaTeX.com \textbf{x} = \left[ \begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f014d740858c61dd437c3f45b93d9276_l3.png) ,
, ![]() denote the coefficient matrix, the variable matrix, and the constant matrix, respectively. The system (2.2) can be expressed as a single vector equation
denote the coefficient matrix, the variable matrix, and the constant matrix, respectively. The system (2.2) can be expressed as a single vector equation
![]()
which in turn can be written as follows:
![]()
Now observe that the vectors appearing on the left side are just the columns
![]()
of the coefficient matrix ![]() . Hence the system (2.2) takes the form
. Hence the system (2.2) takes the form
(2.3) ![]()
This shows that the system (2.2) has a solution if and only if the constant matrix ![]() is a linear combination of the columns of
is a linear combination of the columns of ![]() , and that in this case the entries of the solution are the coefficients
, and that in this case the entries of the solution are the coefficients ![]() ,
, ![]() , and
, and ![]() in this linear combination.
in this linear combination.
Moreover, this holds in general. If ![]() is any
is any ![]() matrix, it is often convenient to view
matrix, it is often convenient to view ![]() as a row of columns. That is, if
as a row of columns. That is, if ![]() are the columns of
are the columns of ![]() , we write
, we write
![]()
and say that ![]() is given in terms of its columns.
is given in terms of its columns.
Now consider any system of linear equations with ![]() coefficient matrix
coefficient matrix ![]() . If
. If ![]() is the constant matrix of the system, and if
is the constant matrix of the system, and if ![Rendered by QuickLaTeX.com \textbf{x} = \left[ \begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-106c7c5485d7f7fc87cca59ba85b2a28_l3.png)
is the matrix of variables then, exactly as above, the system can be written as a single vector equation
(2.4) ![]()
Example 2.2.1
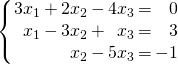
in the form given in (2.4).
Solution:
![Rendered by QuickLaTeX.com \begin{equation*} x_{1} \left[ \begin{array}{r} 3 \\ 1 \\ 0 \end{array} \right] + x_{2} \left[ \begin{array}{r} 2 \\ -3 \\ 1 \end{array} \right] + x_{3} \left[ \begin{array}{r} -4 \\ 1 \\ -5 \end{array} \right] = \left[ \begin{array}{r} 0 \\ 3 \\ -1 \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c1404d3d4fa735227aff6c942086b725_l3.png)
As mentioned above, we view the left side of (2.4) as the product of the matrix ![]() and the vector
and the vector ![]() . This basic idea is formalized in the following definition:
. This basic idea is formalized in the following definition:
Definition 2.5 Matrix-Vector Multiplication
![Rendered by QuickLaTeX.com \textbf{x} = \left[ \begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-106c7c5485d7f7fc87cca59ba85b2a28_l3.png)
is any n-vector, the product
![]()
In other words, if ![]() is
is ![]() and
and ![]() is an
is an ![]() -vector, the product
-vector, the product ![]() is the linear combination of the columns of
is the linear combination of the columns of ![]() where the coefficients are the entries of
where the coefficients are the entries of ![]() (in order).
(in order).
Note that if ![]() is an
is an ![]() matrix, the product
matrix, the product ![]() is only defined if
is only defined if ![]() is an
is an ![]() -vector and then the vector
-vector and then the vector ![]() is an
is an ![]() -vector because this is true of each column
-vector because this is true of each column ![]() of
of ![]() . But in this case the system of linear equations with coefficient matrix
. But in this case the system of linear equations with coefficient matrix ![]() and constant vector
and constant vector ![]() takes the form of a single matrix equation
takes the form of a single matrix equation
![]()
The following theorem combines Definition 2.5 and equation (2.4) and summarizes the above discussion. Recall that a system of linear equations is said to be consistent if it has at least one solution.
Theorem 2.2.1
- Every system of linear equations has the form
 where
where  is the coefficient matrix,
is the coefficient matrix, 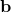 is the constant matrix, and
is the constant matrix, and  is the matrix of variables.
is the matrix of variables. - The system
 is consistent if and only if
is consistent if and only if 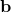 is a linear combination of the columns of
is a linear combination of the columns of 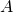 .
. - If
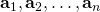 are the columns of
are the columns of 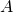 and if
and if ![Rendered by QuickLaTeX.com \textbf{x} = \left[ \begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-106c7c5485d7f7fc87cca59ba85b2a28_l3.png) , then
, then  is a solution to the linear system
is a solution to the linear system  if and only if
if and only if 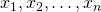 are a solution of the vector equation
are a solution of the vector equation
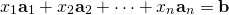
A system of linear equations in the form ![]() as in (1) of Theorem 2.2.1 is said to be written in matrix form. This is a useful way to view linear systems as we shall see.
as in (1) of Theorem 2.2.1 is said to be written in matrix form. This is a useful way to view linear systems as we shall see.
Theorem 2.2.1 transforms the problem of solving the linear system ![]() into the problem of expressing the constant matrix
into the problem of expressing the constant matrix ![]() as a linear combination of the columns of the coefficient matrix
as a linear combination of the columns of the coefficient matrix ![]() . Such a change in perspective is very useful because one approach or the other may be better in a particular situation; the importance of the theorem is that there is a choice.
. Such a change in perspective is very useful because one approach or the other may be better in a particular situation; the importance of the theorem is that there is a choice.
Example 2.2.2
![Rendered by QuickLaTeX.com A = \left[ \begin{array}{rrrr} 2 & -1 & 3 & 5 \\ 0 & 2 & -3 & 1 \\ -3 & 4 & 1 & 2 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-71a850c6d1766fa957cf52cf8c2ef491_l3.png) and
and![Rendered by QuickLaTeX.com \textbf{x} = \left[ \begin{array}{r} 2 \\ 1 \\ 0 \\ -2 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-6c9931265e1a362abea7ad860a6fe19b_l3.png) , compute
, compute Solution:
By Definition 2.5:
![Rendered by QuickLaTeX.com A\textbf{x} = 2 \left[ \begin{array}{r} 2 \\ 0 \\ -3 \end{array} \right] + 1 \left[ \begin{array}{r} -1 \\ 2 \\ 4 \end{array} \right] + 0 \left[ \begin{array}{r} 3 \\ -3 \\ 1 \end{array} \right] - 2 \left[ \begin{array}{r} 5 \\ 1 \\ 2 \end{array} \right] = \left[ \begin{array}{r} -7 \\ 0 \\ -6 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5302649dde2927a9338a2da4e6711af0_l3.png) .
.
Example 2.2.3
Given columns ![]() ,
, ![]() ,
, ![]() , and
, and ![]() in
in ![]() , write
, write ![]() in the form
in the form ![]() where
where ![]() is a matrix and
is a matrix and ![]() is a vector.
is a vector.
Solution:
Here the column of coefficients is
![Rendered by QuickLaTeX.com \textbf{x} = \left[ \begin{array}{r} 2 \\ -3 \\ 5 \\ 1 \end{array} \right].](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-caa9d432222f804c2b3d1ec95fb74f1f_l3.png)
Hence Definition 2.5 gives
![]()
where ![]() is the matrix with
is the matrix with ![]() ,
, ![]() ,
, ![]() , and
, and ![]() as its columns.
as its columns.
Example 2.2.4
Let ![]() be the
be the ![]() matrix given in terms of its columns
matrix given in terms of its columns
![Rendered by QuickLaTeX.com \textbf{a}_{1} = \left[ \begin{array}{r} 2 \\ 0 \\ -1 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-9ad3fa247fd5675f3ace33dcb160eb55_l3.png) ,
, ![Rendered by QuickLaTeX.com \textbf{a}_{2} = \left[ \begin{array}{r} 1 \\ 1 \\ 1 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-fae1cc4cb64558ef193267899832c219_l3.png) ,
, ![Rendered by QuickLaTeX.com \textbf{a}_{3} = \left[ \begin{array}{r} 3 \\ -1 \\ -3 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5215dfeaef4e8513bf6dfddcae012482_l3.png) , and
, and ![Rendered by QuickLaTeX.com \textbf{a}_{4} = \left[ \begin{array}{r} 3 \\ 1 \\ 0 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d4b5864bf23622ea195cf1e70f379925_l3.png) .
.
In each case below, either express ![]() as a linear combination of
as a linear combination of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , or show that it is not such a linear combination. Explain what your answer means for the corresponding system
, or show that it is not such a linear combination. Explain what your answer means for the corresponding system ![]() of linear equations.
of linear equations.
1. ![Rendered by QuickLaTeX.com \textbf{b} = \left[ \begin{array}{r} 1 \\ 2 \\ 3 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-4f4fe6c08b26ba324eebfe368dbb8e7d_l3.png)
2. ![Rendered by QuickLaTeX.com \textbf{b} = \left[ \begin{array}{r} 4 \\ 2 \\ 1 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-4d712ced9ac97ebc8265b0bbb068046d_l3.png)
Solution:
By Theorem 2.2.1, ![]() is a linear combination of
is a linear combination of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() if and only if the system
if and only if the system ![]() is consistent (that is, it has a solution). So in each case we carry the augmented matrix
is consistent (that is, it has a solution). So in each case we carry the augmented matrix ![]() of the system
of the system ![]() to reduced form.
to reduced form.
1. Here
![Rendered by QuickLaTeX.com \left[ \begin{array}{rrrr|r} 2 & 1 & 3 & 3 & 1 \\ 0 & 1 & -1 & 1 & 2 \\ -1 & 1 & -3 & 0 & 3 \end{array} \right] \rightarrow \left[ \begin{array}{rrrr|r} 1 & 0 & 2 & 1 & 0 \\ 0 & 1 & -1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-18edb84ce066f49223dc6a8f2f12658e_l3.png) , so the system
, so the system ![]() has no solution in this case. Hence
has no solution in this case. Hence ![]() is \textit{not} a linear combination of
is \textit{not} a linear combination of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
2. Now
![Rendered by QuickLaTeX.com \left[ \begin{array}{rrrr|r} 2 & 1 & 3 & 3 & 4 \\ 0 & 1 & -1 & 1 & 2 \\ -1 & 1 & -3 & 0 & 1 \end{array} \right] \rightarrow \left[ \begin{array}{rrrr|r} 1 & 0 & 2 & 1 & 1 \\ 0 & 1 & -1 & 1 & 2 \\ 0 & 0 & 0 & 0 & 0 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c74310da472b6032e71831afc81b986e_l3.png) , so the system
, so the system ![]() is consistent.
is consistent.
Thus ![]() is a linear combination of
is a linear combination of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() in this case. In fact the general solution is
in this case. In fact the general solution is ![]() ,
, ![]() ,
, ![]() , and
, and ![]() where
where ![]() and
and ![]() are arbitrary parameters. Hence
are arbitrary parameters. Hence ![Rendered by QuickLaTeX.com x_{1}\textbf{a}_{1} + x_{2}\textbf{a}_{2} + x_{3}\textbf{a}_{3} + x_{4}\textbf{a}_{4} = \textbf{b} = \left[ \begin{array}{r} 4 \\ 2 \\ 1 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f3edcf6f72ca9b418a48fe4b6da8a042_l3.png)
for any choice of ![]() and
and ![]() . If we take
. If we take ![]() and
and ![]() , this becomes
, this becomes ![]() , whereas taking
, whereas taking ![]() gives
gives ![]() .
.
Example 2.2.5
Example 2.2.6
![Rendered by QuickLaTeX.com I = \left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-713bc6c3634032ac1445ed97d0a604ee_l3.png) , show that
, show that Solution:
If ![Rendered by QuickLaTeX.com \textbf{x} = \left[ \begin{array}{r} x_{1} \\ x_{2} \\ x_{3} \end{array} \right],](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c897de4fcf78c69b88c0a8d8b8cbaad7_l3.png) then Definition 2.5 gives
then Definition 2.5 gives
![Rendered by QuickLaTeX.com \begin{equation*} I\textbf{x} = x_{1} \left[ \begin{array}{r} 1 \\ 0 \\ 0 \\ \end{array} \right] + x_{2} \left[ \begin{array}{r} 0 \\ 1 \\ 0 \\ \end{array} \right] + x_{3} \left[ \begin{array}{r} 0 \\ 0 \\ 1 \\ \end{array} \right] = \left[ \begin{array}{r} x_{1} \\ 0 \\ 0 \\ \end{array} \right] + \left[ \begin{array}{r} 0 \\ x_{2} \\ 0 \\ \end{array} \right] + \left[ \begin{array}{r} 0 \\ 0 \\ x_{3} \\ \end{array} \right] = \left[ \begin{array}{r} x_{1} \\ x_{2} \\ x_{3} \\ \end{array} \right] = \textbf{x} \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-31440a006d821ce12da10723f617a933_l3.png)
The matrix ![]() in Example 2.2.6 is called the
in Example 2.2.6 is called the ![]() identity matrix, and we will encounter such matrices again in future. Before proceeding, we develop some algebraic properties of matrix-vector multiplication that are used extensively throughout linear algebra.
identity matrix, and we will encounter such matrices again in future. Before proceeding, we develop some algebraic properties of matrix-vector multiplication that are used extensively throughout linear algebra.
Theorem 2.2.2
Let ![]() and
and ![]() be
be ![]() matrices, and let
matrices, and let ![]() and
and ![]() be
be ![]() -vectors in
-vectors in ![]() . Then:
. Then:
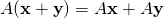 .
. for all scalars
for all scalars  .
. .
.
Proof:
We prove (3); the other verifications are similar and are left as exercises. Let ![]() and
and ![]() be given in terms of their columns. Since adding two matrices is the same as adding their columns, we have
be given in terms of their columns. Since adding two matrices is the same as adding their columns, we have
![]()
If we write ![Rendered by QuickLaTeX.com \textbf{x} = \left[ \begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{array} \right].](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-2252eb90acdfd8ccbba2e52b8be65c49_l3.png)
Definition 2.5 gives

Theorem 2.2.2 allows matrix-vector computations to be carried out much as in ordinary arithmetic. For example, for any ![]() matrices
matrices ![]() and
and ![]() and any
and any ![]() -vectors
-vectors ![]() and
and ![]() , we have:
, we have:
![]()
We will use such manipulations throughout the book, often without mention.
Linear Equations
Theorem 2.2.2 also gives a useful way to describe the solutions to a system
![]()
of linear equations. There is a related system
![]()
called the associated homogeneous system, obtained from the original system ![]() by replacing all the constants by zeros. Suppose
by replacing all the constants by zeros. Suppose ![]() is a solution to
is a solution to ![]() and
and ![]() is a solution to
is a solution to ![]() (that is
(that is ![]() and
and ![]() ). Then
). Then ![]() is another solution to
is another solution to ![]() . Indeed, Theorem 2.2.2 gives
. Indeed, Theorem 2.2.2 gives
![]()
This observation has a useful converse.
Theorem 2.2.3
![]()
for some solution ![]() of the associated homogeneous system
of the associated homogeneous system ![]() .
.
Proof:
Suppose ![]() is also a solution to
is also a solution to ![]() , so that
, so that ![]() . Write
. Write ![]() . Then
. Then ![]() and, using Theorem 2.2.2, we compute
and, using Theorem 2.2.2, we compute
![]()
Hence ![]() is a solution to the associated homogeneous system
is a solution to the associated homogeneous system ![]() .
.
Note that gaussian elimination provides one such representation.
Example 2.2.7
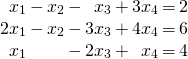
Solution:
Gaussian elimination gives ![]() ,
, ![]() ,
, ![]() , and
, and ![]() where
where ![]() and
and ![]() are arbitrary parameters. Hence the general solution can be written
are arbitrary parameters. Hence the general solution can be written
![Rendered by QuickLaTeX.com \begin{equation*} \textbf{x} = \left[ \begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \end{array} \right] = \left[ \begin{array}{c} 4 + 2s - t \\ 2 + s + 2t \\ s \\ t \end{array} \right] = \left[ \begin{array}{r} 4 \\ 2 \\ 0 \\ 0 \end{array} \right] + \left( s \left[ \begin{array}{r} 2 \\ 1 \\ 1 \\ 0 \end{array} \right] + t \left[ \begin{array}{r} -1 \\ 2 \\ 0 \\ 1 \end{array} \right] \right) \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-ffb756ee748aaa8f00edc0afdfa93da8_l3.png)
Thus
![Rendered by QuickLaTeX.com \textbf{x}_1 = \left[ \begin{array}{r} 4 \\ 2 \\ 0 \\ 0 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-ed5f039acc8324c59130225ab5d86246_l3.png)
is a particular solution (where ![]() ), and
), and
![Rendered by QuickLaTeX.com \textbf{x}_{0} = s \left[ \begin{array}{r} 2 \\ 1 \\ 1 \\ 0 \end{array} \right] + t \left[ \begin{array}{r} -1 \\ 2 \\ 0 \\ 1 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f17840014483e6b964f4bb46b9902e85_l3.png) gives all solutions to the associated homogeneous system. (To see why this is so, carry out the gaussian elimination again but with all the constants set equal to zero.)
gives all solutions to the associated homogeneous system. (To see why this is so, carry out the gaussian elimination again but with all the constants set equal to zero.)
The following useful result is included with no proof.
Theorem 2.2.4
The Dot Product
Definition 2.5 is not always the easiest way to compute a matrix-vector product ![]() because it requires that the columns of
because it requires that the columns of ![]() be explicitly identified. There is another way to find such a product which uses the matrix
be explicitly identified. There is another way to find such a product which uses the matrix ![]() as a whole with no reference to its columns, and hence is useful in practice. The method depends on the following notion.
as a whole with no reference to its columns, and hence is useful in practice. The method depends on the following notion.
Definition 2.6 Dot Product in ![]()
![]()
obtained by multiplying corresponding entries and adding the results.
To see how this relates to matrix products, let ![]() denote a
denote a ![]() matrix and let
matrix and let ![]() be a
be a ![]() -vector. Writing
-vector. Writing
![Rendered by QuickLaTeX.com \begin{equation*} \textbf{x} = \left[ \begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \end{array} \right] \quad \mbox{ and } \quad A = \left[ \begin{array}{cccc} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f3ea80e54da0842279bb70cc14a7e553_l3.png)
in the notation of Section 2.1, we compute
![Rendered by QuickLaTeX.com \begin{align*} A\textbf{x} = \left[ \begin{array}{cccc} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \end{array} \right] \left[ \begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \end{array} \right] &= x_{1} \left[ \begin{array}{c} a_{11} \\ a_{21} \\ a_{31} \end{array} \right] + x_{2} \left[ \begin{array}{c} a_{12} \\ a_{22} \\ a_{32} \end{array} \right] + x_{3} \left[ \begin{array}{c} a_{13} \\ a_{23} \\ a_{33} \end{array} \right] + x_{4} \left[ \begin{array}{c} a_{14} \\ a_{24} \\ a_{34} \end{array} \right] \\ &= \left[ \begin{array}{c} a_{11}x_{1} + a_{12}x_{2} + a_{13}x_{3} + a_{14}x_{4} \\ a_{21}x_{1} + a_{22}x_{2} + a_{23}x_{3} + a_{24}x_{4} \\ a_{31}x_{1} + a_{32}x_{2} + a_{33}x_{3} + a_{34}x_{4} \end{array} \right] \end{align*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f955525af3b1e82deb11d2087f779796_l3.png)
From this we see that each entry of ![]() is the dot product of the corresponding row of
is the dot product of the corresponding row of ![]() with
with ![]() . This computation goes through in general, and we record the result in Theorem 2.2.5.
. This computation goes through in general, and we record the result in Theorem 2.2.5.
Theorem 2.2.5 Dot Product Rule
This result is used extensively throughout linear algebra.
If ![]() is
is ![]() and
and ![]() is an
is an ![]() -vector, the computation of
-vector, the computation of ![]() by the dot product rule is simpler than using Definition 2.5 because the computation can be carried out directly with no explicit reference to the columns of
by the dot product rule is simpler than using Definition 2.5 because the computation can be carried out directly with no explicit reference to the columns of ![]() (as in Definition 2.5. The first entry of
(as in Definition 2.5. The first entry of ![]() is the dot product of row 1 of
is the dot product of row 1 of ![]() with
with ![]() . In hand calculations this is computed by going across row one of
. In hand calculations this is computed by going across row one of ![]() , going down the column
, going down the column ![]() , multiplying corresponding entries, and adding the results. The other entries of
, multiplying corresponding entries, and adding the results. The other entries of ![]() are computed in the same way using the other rows of
are computed in the same way using the other rows of ![]() with the column
with the column ![]() .
.
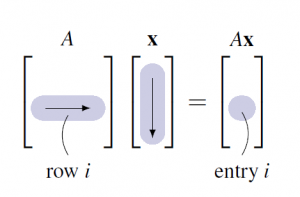
In general, compute entry ![]() of
of ![]() as follows (see the diagram):
as follows (see the diagram):
Go across row ![]() of
of ![]() and down column
and down column ![]() , multiply corresponding entries, and add the results.
, multiply corresponding entries, and add the results.
As an illustration, we rework Example 2.2.2 using the dot product rule instead of Definition 2.5.
Example 2.2.8
![Rendered by QuickLaTeX.com A = \left[ \begin{array}{rrrr} 2 & -1 & 3 & 5 \\ 0 & 2 & -3 & 1 \\ -3 & 4 & 1 & 2 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-71a850c6d1766fa957cf52cf8c2ef491_l3.png)
and
![Rendered by QuickLaTeX.com \textbf{x} = \left[ \begin{array}{r} 2 \\ 1 \\ 0 \\ -2 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-6c9931265e1a362abea7ad860a6fe19b_l3.png) , compute
, compute Solution:
The entries of ![]() are the dot products of the rows of
are the dot products of the rows of ![]() with
with ![]() :
:
![Rendered by QuickLaTeX.com \begin{equation*} A\textbf{x} = \left[ \begin{array}{rrrr} 2 & -1 & 3 & 5 \\ 0 & 2 & -3 & 1 \\ -3 & 4 & 1 & 2 \end{array} \right] \left[ \begin{array}{r} 2 \\ 1 \\ 0 \\ -2 \end{array} \right] = \left[ \begin{array}{rrrrrrr} 2 \cdot 2 & + & (-1)1 & + & 3 \cdot 0 & + & 5(-2) \\ 0 \cdot 2 & + & 2 \cdot 1 & + & (-3)0 & + & 1(-2) \\ (-3)2 & + & 4 \cdot 1 & + & 1 \cdot 0 & + & 2(-2) \end{array} \right] = \left[ \begin{array}{r} -7 \\ 0 \\ -6 \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5a5f96c3d90a54f0e655093b1d5c40c9_l3.png)
Of course, this agrees with the outcome in Example 2.2.2.
Example 2.2.9
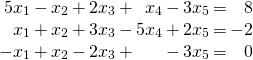
Solution:
Write ![Rendered by QuickLaTeX.com A = \left[ \begin{array}{rrrrr} 5 & -1 & 2 & 1 & -3 \\ 1 & 1 & 3 & -5 & 2 \\ -1 & 1 & -2 & 0 & -3 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-112544d87064dfb0bd7a54fe3140b6ef_l3.png) ,
, ![Rendered by QuickLaTeX.com \textbf{b} = \left[ \begin{array}{r} 8 \\ -2 \\ 0 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f3918bb4bc4a794337ea2f30b7ff96ad_l3.png) , and
, and ![Rendered by QuickLaTeX.com \textbf{x} = \left[ \begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \\ x_{5} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-9dd15327ca7fc6a7383c8109bc157e79_l3.png) . Then the dot product rule gives
. Then the dot product rule gives ![Rendered by QuickLaTeX.com A\textbf{x} = \left[ \arraycolsep=1pt \begin{array}{rrrrrrrrr} 5x_{1} & - & x_{2} & + & 2x_{3} & + & x_{4} & - & 3x_{5} \\ x_{1} & + & x_{2} & + & 3x_{3} & - & 5x_{4} & + & 2x_{5} \\ -x_{1} & + & x_{2} & - & 2x_{3} & & & - & 3x_{5} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-545617a04dedd29a416290f476a81cc9_l3.png) , so the entries of
, so the entries of ![]() are the left sides of the equations in the linear system. Hence the system becomes
are the left sides of the equations in the linear system. Hence the system becomes ![]() because matrices are equal if and only corresponding entries are equal.
because matrices are equal if and only corresponding entries are equal.
Example 2.2.10
If ![]() is the zero
is the zero ![]() matrix, then
matrix, then ![]() for each
for each ![]() -vector
-vector ![]() .
.
Solution:
For each ![]() , entry
, entry ![]() of
of ![]() is the dot product of row
is the dot product of row ![]() of
of ![]() with
with ![]() , and this is zero because row
, and this is zero because row ![]() of
of ![]() consists of zeros.
consists of zeros.
Definition 2.7 The Identity Matrix
The first few identity matrices are
![Rendered by QuickLaTeX.com \begin{equation*} I_{2} = \left[ \begin{array}{rr} 1 & 0 \\ 0 & 1 \end{array} \right], \quad I_{3} = \left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right], \quad I_{4} = \left[ \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right], \quad \dots \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-990bdeed4b6cad3c9d458beecc3e1b31_l3.png)
In Example 2.2.6 we showed that ![]() for each
for each ![]() -vector
-vector ![]() using Definition 2.5. The following result shows that this holds in general, and is the reason for the name.
using Definition 2.5. The following result shows that this holds in general, and is the reason for the name.
Example 2.2.11
Solution:
We verify the case ![]() . Given the
. Given the ![]() -vector
-vector ![Rendered by QuickLaTeX.com \textbf{x} = \left[ \begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-fa849393bb3cfee678eea44076481c2d_l3.png)
the dot product rule gives
![Rendered by QuickLaTeX.com \begin{equation*} I_{4}\textbf{x} = \left[\begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right] \left[ \begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \end{array} \right] = \left[ \begin{array}{c} x_{1} + 0 + 0 + 0 \\ 0 + x_{2} + 0 + 0 \\ 0 + 0 + x_{3} + 0 \\ 0 + 0 + 0 + x_{4} \end{array} \right] = \left[ \begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \end{array} \right] = \vect{x} \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-19ec3618cdc90363702b9cdb2c834ed4_l3.png)
In general, ![]() because entry
because entry ![]() of
of ![]() is the dot product of row
is the dot product of row ![]() of
of ![]() with
with ![]() , and row
, and row ![]() of
of ![]() has
has ![]() in position
in position ![]() and zeros elsewhere.
and zeros elsewhere.
Example 2.2.12
Solution:
Write ![Rendered by QuickLaTeX.com \textbf{e}_{j} = \left[ \begin{array}{c} t_{1} \\ t_{2} \\ \vdots \\ t_{n} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-e6e528df25293d56acf926df82c7cb23_l3.png)
where ![]() , but
, but ![]() for all
for all ![]() . Then Theorem 2.2.5 gives
. Then Theorem 2.2.5 gives
![]()
Example 2.2.12will be referred to later; for now we use it to prove:
Theorem 2.2.6
Proof:
Write ![]() and
and ![]() and in terms of their columns. It is enough to show that
and in terms of their columns. It is enough to show that ![]() holds for all
holds for all ![]() . But we are assuming that
. But we are assuming that ![]() , which gives
, which gives ![]() by Example 2.2.12.
by Example 2.2.12.
We have introduced matrix-vector multiplication as a new way to think about systems of linear equations. But it has several other uses as well. It turns out that many geometric operations can be described using matrix multiplication, and we now investigate how this happens. As a bonus, this description provides a geometric “picture” of a matrix by revealing the effect on a vector when it is multiplied by ![]() . This “geometric view” of matrices is a fundamental tool in understanding them.
. This “geometric view” of matrices is a fundamental tool in understanding them.
2.3 Matrix Multiplication
In Section 2.2 matrix-vector products were introduced. If ![]() is an
is an ![]() matrix, the product
matrix, the product ![]() was defined for any
was defined for any ![]() -column
-column ![]() in
in ![]() as follows: If
as follows: If ![]() where the
where the ![]() are the columns of
are the columns of ![]() , and if
, and if ![Rendered by QuickLaTeX.com \textbf{x} = \left[ \begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-106c7c5485d7f7fc87cca59ba85b2a28_l3.png) ,
,
Definition 2.5 reads
(2.5) ![]()
This was motivated as a way of describing systems of linear equations with coefficient matrix ![]() . Indeed every such system has the form
. Indeed every such system has the form ![]() where
where ![]() is the column of constants.
is the column of constants.
In this section we extend this matrix-vector multiplication to a way of multiplying matrices in general, and then investigate matrix algebra for its own sake. While it shares several properties of ordinary arithmetic, it will soon become clear that matrix arithmetic is different in a number of ways.
Definition 2.9 Matrix Multiplication
![]()
Thus the product matrix ![]() is given in terms of its columns
is given in terms of its columns ![]() : Column
: Column ![]() of
of ![]() is the matrix-vector product
is the matrix-vector product ![]() of
of ![]() and the corresponding column
and the corresponding column ![]() of
of ![]() . Note that each such product
. Note that each such product ![]() makes sense by Definition 2.5 because
makes sense by Definition 2.5 because ![]() is
is ![]() and each
and each ![]() is in
is in ![]() (since
(since ![]() has
has ![]() rows). Note also that if
rows). Note also that if ![]() is a column matrix, this definition reduces to Definition 2.5 for matrix-vector multiplication.
is a column matrix, this definition reduces to Definition 2.5 for matrix-vector multiplication.
Given matrices ![]() and
and ![]() , Definition 2.9 and the above computation give
, Definition 2.9 and the above computation give
![]()
for all ![]() in
in ![]() . We record this for reference.
. We record this for reference.
Theorem 2.3.1
![]()
Here is an example of how to compute the product ![]() of two matrices using Definition 2.9.
of two matrices using Definition 2.9.
Example 2.3.1
![Rendered by QuickLaTeX.com A = \left[ \begin{array}{rrr} 2 & 3 & 5 \\ 1 & 4 & 7 \\ 0 & 1 & 8 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-150065d7fe1fd50383eb17d6412b1738_l3.png)
and
![Rendered by QuickLaTeX.com B = \left[\begin{array}{rr} 8 & 9 \\ 7 & 2 \\ 6 & 1 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-cabec8536af1589b0245e0257dcfd1c9_l3.png) .
.Solution:
The columns of ![]() are
are
![Rendered by QuickLaTeX.com \vec{b}_{1} = \left[ \begin{array}{r} 8 \\ 7 \\ 6 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-be714baaba046440a96a706e8c30ef54_l3.png) and
and ![Rendered by QuickLaTeX.com \vec{b}_{2} = \left[ \begin{array}{r} 9 \\ 2 \\ 1 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-70cdb66551245417b21df563eac9aae9_l3.png) , so Definition 2.5 gives
, so Definition 2.5 gives
![Rendered by QuickLaTeX.com \begin{equation*} A\vec{b}_{1} = \left[ \begin{array}{rrr} 2 & 3 & 5 \\ 1 & 4 & 7 \\ 0 & 1 & 8 \end{array} \right] \left[ \begin{array}{r} 8 \\ 7 \\ 6 \end{array} \right] = \left[ \begin{array}{r} 67 \\ 78 \\ 55 \end{array} \right] \mbox{ and } A\vec{b}_{2} = \left[ \begin{array}{rrr} 2 & 3 & 5 \\ 1 & 4 & 7 \\ 0 & 1 & 8 \end{array} \right] \left[ \begin{array}{r} 9 \\ 2 \\ 1 \end{array} \right] = \left[\begin{array}{r} 29 \\ 24 \\ 10 \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-e078a867223cffb5fcc5ae6efe8d4375_l3.png)
Hence Definition 2.9 above gives ![Rendered by QuickLaTeX.com AB = \left[ \begin{array}{cc} A\vec{b}_{1} & A\vec{b}_{2} \end{array} \right] = \left[ \begin{array}{rr} 67 & 29 \\ 78 & 24 \\ 55 & 10 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-19e38d5e5028c7808ba0f390ef34c203_l3.png) .
.
While Definition 2.9 is important, there is another way to compute the matrix product ![]() that gives a way to calculate each individual entry. In Section 2.2 we defined the dot product of two
that gives a way to calculate each individual entry. In Section 2.2 we defined the dot product of two ![]() -tuples to be the sum of the products of corresponding entries. We went on to show (Theorem 2.2.5) that if
-tuples to be the sum of the products of corresponding entries. We went on to show (Theorem 2.2.5) that if ![]() is an
is an ![]() matrix and
matrix and ![]() is an
is an ![]() -vector, then entry
-vector, then entry ![]() of the product
of the product ![]() is the dot product of row
is the dot product of row ![]() of
of ![]() with
with ![]() . This observation was called the “dot product rule” for matrix-vector multiplication, and the next theorem shows that it extends to matrix multiplication in general.
. This observation was called the “dot product rule” for matrix-vector multiplication, and the next theorem shows that it extends to matrix multiplication in general.
Theorem 2.3.2 Dot Product Rule
product of row
Proof:
Write ![]() in terms of its columns. Then
in terms of its columns. Then ![]() is column
is column ![]() of
of ![]() for each
for each ![]() . Hence the
. Hence the ![]() -entry of
-entry of ![]() is entry
is entry ![]() of
of ![]() , which is the dot product of row
, which is the dot product of row ![]() of
of ![]() with
with ![]() . This proves the theorem.
. This proves the theorem.
Thus to compute the ![]() -entry of
-entry of ![]() , proceed as follows (see the diagram):
, proceed as follows (see the diagram):
Go across row ![]() of
of ![]() , and down column
, and down column ![]() of
of ![]() , multiply corresponding entries, and add the results.
, multiply corresponding entries, and add the results.
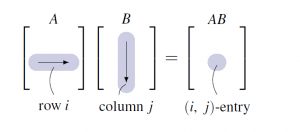
Note that this requires that the rows of ![]() must be the same length as the columns of
must be the same length as the columns of ![]() . The following rule is useful for remembering this and for deciding the size of the product matrix
. The following rule is useful for remembering this and for deciding the size of the product matrix ![]() .
.
Compatibility Rule
Let ![]() and
and ![]() denote matrices. If
denote matrices. If ![]() is
is ![]() and
and ![]() is
is ![]() , the product
, the product ![]() can be formed if and only if
can be formed if and only if ![]() . In this case the size of the product matrix
. In this case the size of the product matrix ![]() is
is ![]() , and we say that
, and we say that ![]() is defined, or that
is defined, or that ![]() and
and ![]() are compatible for multiplication.
are compatible for multiplication.

The diagram provides a useful mnemonic for remembering this. We adopt the following convention:
Whenever a product of matrices is written, it is tacitly assumed that the sizes of the factors are such that the product is defined.
To illustrate the dot product rule, we recompute the matrix product in Example 2.3.1.
Example 2.3.3
![Rendered by QuickLaTeX.com A = \left[ \begin{array}{rrr} 2 & 3 & 5 \\ 1 & 4 & 7 \\ 0 & 1 & 8 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-150065d7fe1fd50383eb17d6412b1738_l3.png)
and
![Rendered by QuickLaTeX.com B = \left[ \begin{array}{rr} 8 & 9 \\ 7 & 2 \\ 6 & 1 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f01a349370b30ab76899f1fe24b42d0d_l3.png) .
.Solution:
Here ![]() is
is ![]() and
and ![]() is
is ![]() , so the product matrix
, so the product matrix ![]() is defined and will be of size
is defined and will be of size ![]() . Theorem 2.3.2 gives each entry of
. Theorem 2.3.2 gives each entry of ![]() as the dot product of the corresponding row of
as the dot product of the corresponding row of ![]() with the corresponding column of
with the corresponding column of ![]() that is,
that is,
![Rendered by QuickLaTeX.com \begin{equation*} AB = \left[ \begin{array}{rrr} 2 & 3 & 5 \\ 1 & 4 & 7 \\ 0 & 1 & 8 \end{array} \right] \left[ \begin{array}{rr} 8 & 9 \\ 7 & 2 \\ 6 & 1 \end{array} \right]= \left[ \arraycolsep=8pt \begin{array}{cc} 2 \cdot 8 + 3 \cdot 7 + 5 \cdot 6 & 2 \cdot 9 + 3 \cdot 2 + 5 \cdot 1 \\ 1 \cdot 8 + 4 \cdot 7 + 7 \cdot 6 & 1 \cdot 9 + 4 \cdot 2 + 7 \cdot 1 \\ 0 \cdot 8 + 1 \cdot 7 + 8 \cdot 6 & 0 \cdot 9 + 1 \cdot 2 + 8 \cdot 1 \end{array} \right] = \left[ \begin{array}{rr} 67 & 29 \\ 78 & 24 \\ 55 & 10 \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-7f81020ed592dab37b83237cc5cb4ce8_l3.png)
Of course, this agrees with Example 2.3.1.
Example 2.3.4
![Rendered by QuickLaTeX.com \begin{equation*} A = \left[ \begin{array}{rrr} 3 & -1 & 2 \\ 0 & 1 & 4 \end{array} \right] \mbox{ and } B = \left[ \begin{array}{rrrr} 2 & 1 & 6 & 0 \\ 0 & 2 & 3 & 4 \\ -1 & 0 & 5 & 8 \end{array} \right]. \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-cbb13e6ee08e2383f978deae780bf269_l3.png)
Then compute ![]() .
.
Solution:
The ![]() -entry of
-entry of ![]() is the dot product of row 1 of
is the dot product of row 1 of ![]() and column 3 of
and column 3 of ![]() (highlighted in the following display), computed by multiplying corresponding entries and adding the results.
(highlighted in the following display), computed by multiplying corresponding entries and adding the results.
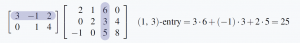
Similarly, the ![]() -entry of
-entry of ![]() involves row 2 of
involves row 2 of ![]() and column 4 of
and column 4 of ![]() .
.

Since ![]() is
is ![]() and
and ![]() is
is ![]() , the product is
, the product is ![]() .
.
![Rendered by QuickLaTeX.com \begin{equation*} AB = \left[ \begin{array}{rrr} 3 & -1 & 2 \\ 0 & 1 & 4 \end{array} \right] \left[ \begin{array}{rrrr} 2 & 1 & 6 & 0 \\ 0 & 2 & 3 & 4 \\ -1 & 0 & 5 & 8 \end{array} \right] = \left[ \begin{array}{rrrr} 4 & 1 & 25 & 12 \\ -4 & 2 & 23 & 36 \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-af24c6d9eac17df7f4c5add5874eb5c5_l3.png)
Example 2.3.5
![Rendered by QuickLaTeX.com B = \left[ \begin{array}{r} 5 \\ 6 \\ 4 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5d2a61617fd897fffc16706f2f2d643c_l3.png) , compute
, compute Solution:
Here, ![]() is a
is a ![]() matrix and
matrix and ![]() is a
is a ![]() matrix, so
matrix, so ![]() and
and ![]() are not defined. However, the compatibility rule reads
are not defined. However, the compatibility rule reads
![]()
so both ![]() and
and ![]() can be formed and these are
can be formed and these are ![]() and
and ![]() matrices, respectively.
matrices, respectively.
![Rendered by QuickLaTeX.com \begin{equation*} AB = \left[ \begin{array}{rrr} 1 & 3 & 2 \end{array} \right] \left[ \begin{array}{r} 5 \\ 6 \\ 4 \end{array} \right] = \left[ \begin{array}{c} 1 \cdot 5 + 3 \cdot 6 + 2 \cdot 4 \end{array} \right] = \arraycolsep=1.5pt \left[ \begin{array}{c} 31 \end{array}\right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-7afabbff2e1ff7670ae95558fc8eff68_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} BA = \left[ \begin{array}{r} 5 \\ 6 \\ 4 \end{array} \right] \left[ \begin{array}{rrr} 1 & 3 & 2 \end{array} \right] = \left[ \begin{array}{rrr} 5 \cdot 1 & 5 \cdot 3 & 5 \cdot 2 \\ 6 \cdot 1 & 6 \cdot 3 & 6 \cdot 2 \\ 4 \cdot 1 & 4 \cdot 3 & 4 \cdot 2 \end{array} \right] = \left[ \begin{array}{rrr} 5 & 15 & 10 \\ 6 & 18 & 12 \\ 4 & 12 & 8 \end{array} \right \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-20ecc1edfb2243fbba8a7f827b72adc7_l3.png)
Unlike numerical multiplication, matrix products ![]() and
and ![]() need not be equal. In fact they need not even be the same size, as Example 2.3.5 shows. It turns out to be rare that
need not be equal. In fact they need not even be the same size, as Example 2.3.5 shows. It turns out to be rare that ![]() (although it is by no means impossible), and
(although it is by no means impossible), and ![]() and
and ![]() are said to commute when this happens.
are said to commute when this happens.
Example 2.3.6
Solution:
![]() , so
, so ![]() can occur even if
can occur even if ![]() . Next,
. Next,
![Rendered by QuickLaTeX.com \begin{align*} AB & = \left[ \begin{array}{rr} 6 & 9 \\ -4 & -6 \end{array} \right] \left[ \begin{array}{rr} 1 & 2 \\ -1 & 0 \end{array} \right] = \left[ \begin{array}{rr} -3 & 12 \\ 2 & -8 \end{array} \right] \\ BA & = \left[ \begin{array}{rr} 1 & 2 \\ -1 & 0 \end{array} \right] \left[ \begin{array}{rr} 6 & 9 \\ -4 & -6 \end{array} \right] = \left[ \begin{array}{rr} -2 & -3 \\ -6 & -9 \end{array} \right] \end{align*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-90f6044a494dc0f209c0325f1b5eddd6_l3.png)
Hence ![]() , even though
, even though ![]() and
and ![]() are the same size.
are the same size.
Example 2.3.7
Solution:
These both follow from the dot product rule as the reader should verify. For a more formal proof, write ![]() where
where ![]() is column
is column ![]() of
of ![]() . Then Definition 2.9 and Example 2.2.1 give
. Then Definition 2.9 and Example 2.2.1 give
![]()
If ![]() denotes column
denotes column ![]() of
of ![]() , then
, then ![]() for each
for each ![]() by Example 2.2.12. Hence Definition 2.9 gives:
by Example 2.2.12. Hence Definition 2.9 gives:
![]()
The following theorem collects several results about matrix multiplication that are used everywhere in linear algebra.
Theorem 2.3.3
Assume that ![]() is any scalar, and that
is any scalar, and that ![]() ,
, ![]() , and
, and ![]() are matrices of sizes such that the indicated matrix products are defined. Then:
are matrices of sizes such that the indicated matrix products are defined. Then:
1. ![]() and
and ![]() where
where ![]() denotes an identity matrix.
denotes an identity matrix.
2. ![]() .
.
3. ![]() .
.
4. ![]() .
.
5. ![]() .
.
6. ![]() .
.
Proof:
Condition (1) is Example 2.3.7; we prove (2), (4), and (6) and leave (3) and (5) as exercises.
1. If ![]() in terms of its columns, then
in terms of its columns, then ![]() by Definition 2.9, so
by Definition 2.9, so
![Rendered by QuickLaTeX.com \begin{equation*} \begin{array}{lllll} A(BC) & = & \left[ \begin{array}{rrrr} A(B\vec{c}_{1}) & A(B\vec{c}_{2}) & \cdots & A(B\vec{c}_{k}) \end{array} \right] & & \mbox{Definition 2.9} \\ & & & & \\ & = & \left[ \begin{array}{rrrr} (AB)\vec{c}_{1} & (AB)\vec{c}_{2} & \cdots & (AB)\vec{c}_{k}) \end{array} \right] & & \mbox{Theorem 2.3.1} \\ & & & & \\ & = & (AB)C & & \mbox{Definition 2.9} \end{array} \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-a554ce3a1b2e5bb6eab4b1347e58f982_l3.png)
4. We know (Theorem 2.2.) that ![]() holds for every column
holds for every column ![]() . If we write
. If we write ![]() in terms of its columns, we get
in terms of its columns, we get
![Rendered by QuickLaTeX.com \begin{equation*} \begin{array}{lllll} (B + C)A & = & \left[ \begin{array}{rrrr} (B + C)\vec{a}_{1} & (B + C)\vec{a}_{2} & \cdots & (B + C)\vec{a}_{n} \end{array} \right] & & \mbox{Definition 2.9} \\ & & & & \\ & = & \left[ \begin{array}{rrrr} B\vec{a}_{1} + C\vec{a}_{1} & B\vec{a}_{2} + C\vec{a}_{2} & \cdots & B\vec{a}_{n} + C\vec{a}_{n} \end{array} \right] & & \mbox{Theorem 2.2.2} \\ & & & & \\ & = & \left[ \begin{array}{rrrr} B\vec{a}_{1} & B\vec{a}_{2} & \cdots & B\vec{a}_{n} \end{array} \right] + \left[ \begin{array}{rrrr} C\vec{a}_{1} & C\vec{a}_{2} & \cdots & C\vec{a}_{n} \end{array} \right] & & \mbox{Adding Columns} \\ & & & & \\ & = & BA + CA & & \mbox{Definition 2.9} \end{array} \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-cc87d4b3237ecf4f370a1a69712fae1e_l3.png)
6. As in Section 2.1, write ![]() and
and ![]() , so that
, so that ![]() and
and ![]() where
where ![]() and
and ![]() for all
for all ![]() and
and ![]() . If
. If ![]() denotes the
denotes the ![]() -entry of
-entry of ![]() , then
, then ![]() is the dot product of row
is the dot product of row ![]() of
of ![]() with column
with column ![]() of
of ![]() . Hence
. Hence

But this is the dot product of row ![]() of
of ![]() with column
with column ![]() of
of ![]() ; that is, the
; that is, the ![]() -entry of
-entry of ![]() ; that is, the
; that is, the ![]() -entry of
-entry of ![]() . This proves (6).
. This proves (6).
Property 2 in Theorem 2.3.3 is called the associative law of matrix multiplication. It asserts that the equation ![]() holds for all matrices (if the products are defined). Hence this product is the same no matter how it is formed, and so is written simply as
holds for all matrices (if the products are defined). Hence this product is the same no matter how it is formed, and so is written simply as ![]() . This extends: The product
. This extends: The product ![]() of four matrices can be formed several ways—for example,
of four matrices can be formed several ways—for example, ![]() ,
, ![]() , and
, and ![]() —but the associative law implies that they are all equal and so are written as
—but the associative law implies that they are all equal and so are written as ![]() . A similar remark applies in general: Matrix products can be written unambiguously with no parentheses.
. A similar remark applies in general: Matrix products can be written unambiguously with no parentheses.
However, a note of caution about matrix multiplication must be taken: The fact that ![]() and
and ![]() need not be equal means that the order of the factors is important in a product of matrices. For example
need not be equal means that the order of the factors is important in a product of matrices. For example ![]() and
and ![]() may not be equal.
may not be equal.
Warning:
If the order of the factors in a product of matrices is changed, the product matrix may change (or may not be defined). Ignoring this warning is a source of many errors by students of linear algebra!}
Properties 3 and 4 in Theorem 2.3.3 are called distributive laws. They assert that ![]() and
and ![]() hold whenever the sums and products are defined. These rules extend to more than two terms and, together with Property 5, ensure that many manipulations familiar from ordinary algebra extend to matrices. For example
hold whenever the sums and products are defined. These rules extend to more than two terms and, together with Property 5, ensure that many manipulations familiar from ordinary algebra extend to matrices. For example
![]()
Note again that the warning is in effect: For example ![]() need not equal
need not equal ![]() . These rules make possible a lot of simplification of matrix expressions.
. These rules make possible a lot of simplification of matrix expressions.
Example 2.3.8
Solution:
Example 2.3.9 and Example 2.3.10 below show how we can use the properties in Theorem 2.3.2to deduce other facts about matrix multiplication. Matrices ![]() and
and ![]() are said to commute if
are said to commute if ![]() .
.
Example 2.3.9
Solution:
Showing that ![]() commutes with
commutes with ![]() means verifying that
means verifying that ![]() . The computation uses the associative law several times, as well as the given facts that
. The computation uses the associative law several times, as well as the given facts that ![]() and
and ![]() .
.
![]()
Example 2.3.10
Solution:
The following always holds:
(2.6) ![]()
Hence if ![]() , then
, then ![]() follows. Conversely, if this last equation holds, then equation (2.6 becomes
follows. Conversely, if this last equation holds, then equation (2.6 becomes
![]()
This gives ![]() , and
, and ![]() follows.
follows.
In Section 2.2 we saw (in Theorem 2.2.1 ) that every system of linear equations has the form
![]()
where ![]() is the coefficient matrix,
is the coefficient matrix, ![]() is the column of variables, and
is the column of variables, and ![]() is the constant matrix. Thus the system of linear equations becomes a single matrix equation. Matrix multiplication can yield information about such a system.
is the constant matrix. Thus the system of linear equations becomes a single matrix equation. Matrix multiplication can yield information about such a system.
Example 2.3.11
Solution:
Suppose that ![]() is any solution to the system, so that
is any solution to the system, so that ![]() . Multiply both sides of this matrix equation by
. Multiply both sides of this matrix equation by ![]() to obtain, successively,
to obtain, successively,
![]()
This shows that if the system has a solution ![]() , then that solution must be
, then that solution must be ![]() , as required. But it does not guarantee that the system has a solution. However, if we write
, as required. But it does not guarantee that the system has a solution. However, if we write ![]() , then
, then
![]()
Thus ![]() will be a solution if the condition
will be a solution if the condition ![]() is satisfied.
is satisfied.
The ideas in Example 2.3.11 lead to important information about matrices; this will be pursued in the next section.
2.4 Matrix Inverse
Three basic operations on matrices, addition, multiplication, and subtraction, are analogs for matrices of the same operations for numbers. In this section we introduce the matrix analog of numerical division.
To begin, consider how a numerical equation ![]() is solved when
is solved when ![]() and
and ![]() are known numbers. If
are known numbers. If ![]() , there is no solution (unless
, there is no solution (unless ![]() ). But if
). But if ![]() , we can multiply both sides by the inverse
, we can multiply both sides by the inverse ![]() to obtain the solution
to obtain the solution ![]() . Of course multiplying by
. Of course multiplying by ![]() is just dividing by
is just dividing by ![]() , and the property of
, and the property of ![]() that makes this work is that
that makes this work is that ![]() . Moreover, we saw in Section~?? that the role that
. Moreover, we saw in Section~?? that the role that ![]() plays in arithmetic is played in matrix algebra by the identity matrix
plays in arithmetic is played in matrix algebra by the identity matrix ![]() . This suggests the following definition.
. This suggests the following definition.
Definition 2.11 Matrix Inverses
![]()
A matrix ![]() that has an inverse is called an
that has an inverse is called an ![]()
Note that only square matrices have inverses. Even though it is plausible that nonsquare matrices ![]() and
and ![]() could exist such that
could exist such that ![]() and
and ![]() , where
, where ![]() is
is ![]() and
and ![]() is
is ![]() , we claim that this forces
, we claim that this forces ![]() . Indeed, if
. Indeed, if ![]() there exists a nonzero column
there exists a nonzero column ![]() such that
such that ![]() (by Theorem 1.3.1), so
(by Theorem 1.3.1), so ![]() , a contradiction. Hence
, a contradiction. Hence ![]() . Similarly, the condition
. Similarly, the condition ![]() implies that
implies that ![]() . Hence
. Hence ![]() so
so ![]() is square.}
is square.}
Example 2.4.1
is an inverse of
Solution:
Compute ![]() and
and ![]() .
.
![]()
Hence ![]() , so
, so ![]() is indeed an inverse of
is indeed an inverse of ![]() .
.
Example 2.4.2
has no inverse.
Solution:
Let ![]()
denote an arbitrary ![]() matrix. Then
matrix. Then
![]()
so ![]() has a row of zeros. Hence
has a row of zeros. Hence ![]() cannot equal
cannot equal ![]() for any
for any ![]() .
.
The argument in Example 2.4.2 shows that no zero matrix has an inverse. But Example 2.4.2 also shows that, unlike arithmetic, it is possible for a nonzero matrix to have no inverse. However, if a matrix does have an inverse, it has only one.
Theorem 2.4.1
Proof:
Since ![]() and
and ![]() are both inverses of
are both inverses of ![]() , we have
, we have ![]() . Hence
. Hence
![]()
If ![]() is an invertible matrix, the (unique) inverse of
is an invertible matrix, the (unique) inverse of ![]() is denoted
is denoted ![]() . Hence
. Hence ![]() (when it exists) is a square matrix of the same size as
(when it exists) is a square matrix of the same size as ![]() with the property that
with the property that
![]()
These equations characterize ![]() in the following sense:
in the following sense:
Inverse Criterion: If somehow a matrix ![]() can be found such that
can be found such that ![]() and
and ![]() , then
, then ![]() is invertible and
is invertible and ![]() is the inverse of
is the inverse of ![]() ; in symbols,
; in symbols, ![]() .}
.}
This is a way to verify that the inverse of a matrix exists. Example 2.3.3 and Example 2.3.4 offer illustrations.
Example 2.4.3
Solution:
We have ![]() , and so
, and so
![]()
Hence ![]() , as asserted. This can be written as
, as asserted. This can be written as ![]() , so it shows that
, so it shows that ![]() is the inverse of
is the inverse of ![]() . That is,
. That is, ![]() .
.
The next example presents a useful formula for the inverse of a ![]() matrix
matrix ![]() when it exists. To state it, we define the
when it exists. To state it, we define the ![]()
![]() and the
and the ![]()
![]() of the matrix
of the matrix ![]() as follows:
as follows:
![]()
Example 2.4.4
![]()
Solution:
For convenience, write ![]() and
and
![]() . Then
. Then ![]() as the reader can verify. So if
as the reader can verify. So if ![]() , scalar multiplication by
, scalar multiplication by ![]() gives
gives
![]()
Hence ![]() is invertible and
is invertible and ![]() . Thus it remains only to show that if
. Thus it remains only to show that if ![]() exists, then
exists, then ![]() .
.
We prove this by showing that assuming ![]() leads to a contradiction. In fact, if
leads to a contradiction. In fact, if ![]() , then
, then ![]() , so left multiplication by
, so left multiplication by ![]() gives
gives ![]() ; that is,
; that is, ![]() , so
, so ![]() . But this implies that
. But this implies that ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are all zero, so
are all zero, so ![]() , contrary to the assumption that
, contrary to the assumption that ![]() exists.
exists.
As an illustration, if ![]()
then ![]() . Hence
. Hence ![]() is invertible and
is invertible and ![]() , as the reader is invited to verify.
, as the reader is invited to verify.
The determinant and adjugate will be defined in Chapter 3 for any square matrix, and the conclusions in Example 2.4.4 will be proved in full generality.
Inverse and Linear systems
Matrix inverses can be used to solve certain systems of linear equations. Recall that a ![]() of linear equations can be written as a
of linear equations can be written as a ![]() matrix equation
matrix equation
![]()
where ![]() and
and ![]() are known and
are known and ![]() is to be determined. If
is to be determined. If ![]() is invertible, we multiply each side of the equation on the left by
is invertible, we multiply each side of the equation on the left by ![]() to get
to get
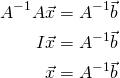
This gives the solution to the system of equations (the reader should verify that ![]() really does satisfy
really does satisfy ![]() ). Furthermore, the argument shows that if
). Furthermore, the argument shows that if ![]() is
is ![]() solution, then necessarily
solution, then necessarily ![]() , so the solution is unique. Of course the technique works only when the coefficient matrix
, so the solution is unique. Of course the technique works only when the coefficient matrix ![]() has an inverse. This proves Theorem 2.4.2.
has an inverse. This proves Theorem 2.4.2.
Theorem 2.4.2
![]()
If the ![]() coefficient matrix
coefficient matrix ![]() is invertible, the system has the unique solution
is invertible, the system has the unique solution
![]()
Example 2.4.5
Solution:
In matrix form this is ![]() where
where ![]() ,
, ![]() , and
, and ![]() . Then
. Then ![]() , so
, so ![]() is invertible and
is invertible and ![]()
by Example 2.4.4. Thus Theorem 2.4.2 gives
![]()
so the solution is ![]() and
and ![]() .
.
An inversion method
If a matrix ![]() is
is ![]() and invertible, it is desirable to have an efficient technique for finding the inverse. The following procedure will be justified in Section 2.5.
and invertible, it is desirable to have an efficient technique for finding the inverse. The following procedure will be justified in Section 2.5.
Matrix Inversion Algorithm
![]()
where the row operations on ![]() and
and ![]() are carried out simultaneously.
are carried out simultaneously.
Example 2.4.6
![Rendered by QuickLaTeX.com \begin{equation*} A = \left[ \begin{array}{rrr} 2 & 7 & 1 \\ 1 & 4 & -1 \\ 1 & 3 & 0 \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f40d95ed68a3b8d4a6293659f7805c46_l3.png)
Solution:
Apply elementary row operations to the double matrix
![Rendered by QuickLaTeX.com \begin{equation*} \left[ \begin{array}{rrr} A & I \end{array} \right] = \left[ \begin{array}{rrr|rrr} 2 & 7 & 1 & 1 & 0 & 0 \\ 1 & 4 & -1 & 0 & 1 & 0 \\ 1 & 3 & 0 & 0 & 0 & 1 \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-cc78fbe2bc855fe2f21553358eb7c9b6_l3.png)
so as to carry ![]() to
to ![]() . First interchange rows 1 and 2.
. First interchange rows 1 and 2.
![Rendered by QuickLaTeX.com \begin{equation*} \left[ \begin{array}{rrr|rrr} 1 & 4 & -1 & 0 & 1 & 0 \\ 2 & 7 & 1 & 1 & 0 & 0 \\ 1 & 3 & 0 & 0 & 0 & 1 \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c6486d76c87127a5b2773ea9d7c1788b_l3.png)
Next subtract ![]() times row 1 from row 2, and subtract row 1 from row 3.
times row 1 from row 2, and subtract row 1 from row 3.
![Rendered by QuickLaTeX.com \begin{equation*} \left[ \begin{array}{rrr|rrr} 1 & 4 & -1 & 0 & 1 & 0 \\ 0 & -1 & 3 & 1 & -2 & 0 \\ 0 & -1 & 1 & 0 & -1 & 1 \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-fc2e64ffa0839ad2654b1c0c77b0106e_l3.png)
Continue to reduced row-echelon form.
![Rendered by QuickLaTeX.com \begin{equation*} \left[ \begin{array}{rrr|rrr} 1 & 0 & 11 & 4 & -7 & 0 \\ 0 & 1 & -3 & -1 & 2 & 0 \\ 0 & 0 & -2 & -1 & 1 & 1 \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-bae649907a67ba339bb403be2de79cac_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \left[ \def\arraystretch{1.5} \begin{array}{rrr|rrr} 1 & 0 & 0 & \frac{-3}{2} & \frac{-3}{2} & \frac{11}{2} \\ 0 & 1 & 0 & \frac{1}{2} & \frac{1}{2} & \frac{-3}{2} \\ 0 & 0 & 1 & \frac{1}{2} & \frac{-1}{2} & \frac{-1}{2} \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-059b8d000f37736c6eb3c83482e882ed_l3.png)
Hence ![Rendered by QuickLaTeX.com A^{-1} = \frac{1}{2} \left[ \begin{array}{rrr} -3 & -3 & 11 \\ 1 & 1 & -3 \\ 1 & -1 & -1 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-b789ae7ef4f2e2763174c4eece831580_l3.png) , as is readily verified.
, as is readily verified.
Given any ![]() matrix
matrix ![]() , Theorem 1.2.1 shows that
, Theorem 1.2.1 shows that ![]() can be carried by elementary row operations to a matrix
can be carried by elementary row operations to a matrix ![]() in reduced row-echelon form. If
in reduced row-echelon form. If ![]() , the matrix
, the matrix ![]() is invertible (this will be proved in the next section), so the algorithm produces
is invertible (this will be proved in the next section), so the algorithm produces ![]() . If
. If ![]() , then
, then ![]() has a row of zeros (it is square), so no system of linear equations
has a row of zeros (it is square), so no system of linear equations ![]() can have a unique solution. But then
can have a unique solution. But then ![]() is not invertible by Theorem 2.4.2. Hence, the algorithm is effective in the sense conveyed in Theorem 2.4.3.
is not invertible by Theorem 2.4.2. Hence, the algorithm is effective in the sense conveyed in Theorem 2.4.3.
Theorem 2.4.3
first case, the algorithm produces
Properties of inverses
The following properties of an invertible matrix are used everywhere.
Example 2.4.7: Cancellation Laws
Let ![]() be an invertible matrix. Show that:
be an invertible matrix. Show that:
1. If ![]() , then
, then ![]() .
.
2. If ![]() , then
, then ![]() .
.
Solution:
Given the equation ![]() , left multiply both sides by
, left multiply both sides by ![]() to obtain
to obtain ![]() . Thus
. Thus ![]() , that is
, that is ![]() . This proves (1) and the proof of (2) is left to the reader.
. This proves (1) and the proof of (2) is left to the reader.
Properties (1) and (2) in Example 2.4.7 are described by saying that an invertible matrix can be “left cancelled” and “right cancelled”, respectively. Note however that “mixed” cancellation does not hold in general: If ![]() is invertible and
is invertible and ![]() , then
, then ![]() and
and ![]() may
may ![]() be equal, even if both are
be equal, even if both are ![]() . Here is a specific example:
. Here is a specific example:
![]()
Sometimes the inverse of a matrix is given by a formula. Example 2.4.4 is one illustration; Example 2.4.8 and Example 2.4.9 provide two more. The idea is the ![]() : If a matrix
: If a matrix ![]() can be found such that
can be found such that ![]() , then
, then ![]() is invertible and
is invertible and ![]() .
.
Example 2.4.8
Solution:
![]() exists (by assumption). Its transpose
exists (by assumption). Its transpose ![]() is the candidate proposed for the inverse of
is the candidate proposed for the inverse of ![]() . Using the inverse criterion, we test it as follows:
. Using the inverse criterion, we test it as follows:
![]()
Hence ![]() is indeed the inverse of
is indeed the inverse of ![]() ; that is,
; that is, ![]() .
.
Example 2.4.9
Solution:
We are given a candidate for the inverse of ![]() , namely
, namely ![]() . We test it as follows:
. We test it as follows:
![]()
Hence ![]() is the inverse of
is the inverse of ![]() ; in symbols,
; in symbols, ![]() .
.
We now collect several basic properties of matrix inverses for reference.
Theorem 2.4.4
All the following matrices are square matrices of the same size.
1. ![]() is invertible and
is invertible and ![]() .
.
2. If ![]() is invertible, so is
is invertible, so is ![]() , and
, and ![]() .
.
3. If ![]() and
and ![]() are invertible, so is
are invertible, so is ![]() , and
, and ![]() .
.
4. If ![]() are all invertible, so is their product
are all invertible, so is their product ![]() , and
, and
![]()
5. If ![]() is invertible, so is
is invertible, so is ![]() for any
for any ![]() , and
, and ![]() .
.
6. If ![]() is invertible and
is invertible and ![]() is a number, then
is a number, then ![]() is invertible and
is invertible and ![]() .
.
7. If ![]() is invertible, so is its transpose
is invertible, so is its transpose ![]() , and
, and ![]() .
.
Proof:
1. This is an immediate consequence of the fact that ![]() .
.
2. The equations ![]() show that
show that ![]() is the inverse of
is the inverse of ![]() ; in symbols,
; in symbols, ![]() .
.
3. This is Example 2.4.9.
4. Use induction on ![]() . If
. If ![]() , there is nothing to prove, and if
, there is nothing to prove, and if ![]() , the result is property 3. If
, the result is property 3. If ![]() , assume inductively that
, assume inductively that ![]() . We apply this fact together with property 3 as follows:
. We apply this fact together with property 3 as follows:
![Rendered by QuickLaTeX.com \begin{align*} \left[ A_{1}A_{2} \cdots A_{k-1}A_{k} \right]^{-1} &= \left[ \left(A_{1}A_{2} \cdots A_{k-1}\right)A_{k} \right]^{-1} \\ &= A_{k}^{-1}\left(A_{1}A_{2} \cdots A_{k-1}\right)^{-1} \\ &= A_{k}^{-1}\left(A_{k-1}^{-1} \cdots A_{2}^{-1}A_{1}^{-1}\right) \end{align*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-dad725397856b469c17d774d7c6b7f23_l3.png)
So the proof by induction is complete.
5. This is property 4 with ![]() .
.
6. The readers are invited to verify it.
7. This is Example 2.4.8.
The reversal of the order of the inverses in properties 3 and 4 of Theorem 2.4.4 is a consequence of the fact that matrix multiplication is not
commutative. Another manifestation of this comes when matrix equations are dealt with. If a matrix equation ![]() is given, it can be
is given, it can be ![]() by a matrix
by a matrix ![]() to yield
to yield ![]() . Similarly,
. Similarly, ![]() gives
gives ![]() . However, we cannot mix the two: If
. However, we cannot mix the two: If ![]() , it need
, it need ![]() be the case that
be the case that ![]() even if
even if ![]() is invertible, for example,
is invertible, for example, ![]() ,
, ![]() .
.
Part 7 of Theorem 2.4.4 together with the fact that ![]() gives
gives
Corollary 2.4.1
Example 2.4.10
Solution:
By Theorem 2.4.2 (2) and Example 2.4.4, we have
![]()
Hence ![]() , so
, so ![]()
by Theorem 2.4.4(7).
The following important theorem collects a number of conditions all equivalent to invertibility. It will be referred to frequently below.
Theorem 2.4.5 Inverse Theorem
The following conditions are equivalent for an ![]() matrix
matrix ![]() :
:
1. ![]() is invertible.
is invertible.
2. The homogeneous system ![]() has only the trivial solution
has only the trivial solution ![]() .
.
3. ![]() can be carried to the identity matrix
can be carried to the identity matrix ![]() by elementary row operations.
by elementary row operations.
4. The system ![]() has at least one solution
has at least one solution ![]() for every choice of column
for every choice of column ![]() .
.
5. There exists an ![]() matrix
matrix ![]() such that
such that ![]() .
.
Proof:
We show that each of these conditions implies the next, and that (5) implies (1).
(1) ![]() (2). If
(2). If ![]() exists, then
exists, then ![]() gives
gives ![]() .
.
(2) ![]() (3). Assume that (2) is true. Certainly
(3). Assume that (2) is true. Certainly ![]() by row operations where
by row operations where ![]() is a reduced, row-echelon matrix. It suffices to show that
is a reduced, row-echelon matrix. It suffices to show that ![]() . Suppose that this is not the case. Then
. Suppose that this is not the case. Then ![]() has a row of zeros (being square). Now consider the augmented matrix
has a row of zeros (being square). Now consider the augmented matrix ![]() of the system
of the system ![]() . Then
. Then ![]() is the reduced form, and
is the reduced form, and ![]() also has a row of zeros. Since
also has a row of zeros. Since ![]() is square there must be at least one nonleading variable, and hence at least one parameter. Hence the system
is square there must be at least one nonleading variable, and hence at least one parameter. Hence the system ![]() has infinitely many solutions, contrary to (2). So
has infinitely many solutions, contrary to (2). So ![]() after all.
after all.
(3) ![]() (4). Consider the augmented matrix
(4). Consider the augmented matrix ![]() of the system
of the system ![]() . Using (3), let
. Using (3), let ![]() by a sequence of row operations. Then these same operations carry
by a sequence of row operations. Then these same operations carry ![]() for some column
for some column ![]() . Hence the system
. Hence the system ![]() has a solution (in fact unique) by gaussian elimination. This proves (4).
has a solution (in fact unique) by gaussian elimination. This proves (4).
(4) ![]() (5). Write
(5). Write ![]() where
where ![]() are the columns of
are the columns of ![]() . For each \newline
. For each \newline ![]() , the system
, the system ![]() has a solution
has a solution ![]() by (4), so
by (4), so ![]() . Now let
. Now let ![]() be the
be the ![]() matrix with these matrices
matrix with these matrices ![]() as its columns. Then Definition 2.9 gives (5):
as its columns. Then Definition 2.9 gives (5):
![]()
(5) ![]() (1). Assume that (5) is true so that
(1). Assume that (5) is true so that ![]() for some matrix
for some matrix ![]() . Then
. Then ![]() implies
implies ![]() (because
(because ![]() ). Thus condition (2) holds for the matrix
). Thus condition (2) holds for the matrix ![]() rather than
rather than ![]() . Hence the argument above that (2)
. Hence the argument above that (2) ![]() (3)
(3) ![]() (4)
(4) ![]() (5) (with
(5) (with ![]() replaced by
replaced by ![]() ) shows that a matrix
) shows that a matrix ![]() exists such that
exists such that ![]() . But then
. But then
![]()
Thus ![]() which, together with
which, together with ![]() , shows that
, shows that ![]() is the inverse of
is the inverse of ![]() . This proves (1).
. This proves (1).
The proof of (5) ![]() (1) in Theorem 2.4.5 shows that if
(1) in Theorem 2.4.5 shows that if ![]() for square matrices, then necessarily
for square matrices, then necessarily ![]() , and hence that
, and hence that ![]() and
and ![]() are inverses of each other. We record this important fact for reference.
are inverses of each other. We record this important fact for reference.
Corollary 2.4.1
Here is a quick way to remember Corollary 2.4.1. If ![]() is a square matrix, then
is a square matrix, then
1. If ![]() then
then ![]() .
.
2. If ![]() then
then ![]() .
.
Observe that Corollary 2.4.1 is false if ![]() and
and ![]() are not square matrices. For example, we have
are not square matrices. For example, we have
![Rendered by QuickLaTeX.com \begin{equation*} \left[ \begin{array}{rrr} 1 & 2 & 1 \\ 1 & 1 & 1 \end{array} \right] \left[ \begin{array}{rr} -1 & 1 \\ 1 & -1 \\ 0 & 1 \end{array} \right] = I_{2} \quad \mbox{ but } \left[ \begin{array}{rr} -1 & 1 \\ 1 & -1 \\ 0 & 1 \end{array} \right] \left[ \begin{array}{rrr} 1 & 2 & 1 \\ 1 & 1 & 1 \end{array} \right] \neq I_{3} \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-1609874c4259626ab7f7448cf0e12644_l3.png)
In fact, it can be verified that if ![]() and
and ![]() , where
, where ![]() is
is ![]() and
and ![]() is
is ![]() , then
, then ![]() and
and ![]() and
and ![]() are (square) inverses of each other.
are (square) inverses of each other.
An ![]() matrix
matrix ![]() has
has ![]() if and only if (3) of Theorem 2.4.5 holds. Hence
if and only if (3) of Theorem 2.4.5 holds. Hence
Corollary 2.4.2

