3 Determinants and Diagonalization
Introduction
With each square matrix we can calculate a number, called the determinant of the matrix, which tells us whether or not the matrix is invertible. In fact, determinants can be used to give a formula for the inverse of a matrix. They also arise in calculating certain numbers (called eigenvalues) associated with the matrix. These eigenvalues are essential to a technique called diagonalization that is used in many applications where it is desired to predict the future behaviour of a system. For example, we use it to predict whether a species will become extinct.
Determinants were first studied by Leibnitz in 1696, and the term “determinant” was first used in 1801 by Gauss is his Disquisitiones Arithmeticae. Determinants are much older than matrices (which were introduced by Cayley in 1878) and were used extensively in the eighteenth and nineteenth centuries, primarily because of their significance in geometry. Although they are somewhat less important today, determinants still play a role in the theory and application of matrix algebra.
3.1 The Cofactor Expansion
In Section 2.4, we defined the determinant of a ![]() matrix
matrix
![]()
as follows:
![]()
and showed (in Example 2.4.4) that ![]() has an inverse if and only if det
has an inverse if and only if det ![]() . One objective of this chapter is to do this for any square matrix A. There is no difficulty for
. One objective of this chapter is to do this for any square matrix A. There is no difficulty for ![]() matrices: If
matrices: If ![]() , we define
, we define ![]() and note that
and note that ![]() is invertible if and only if
is invertible if and only if ![]() .
.
If ![]() is
is ![]() and invertible, we look for a suitable definition of
and invertible, we look for a suitable definition of ![]() by trying to carry
by trying to carry ![]() to the identity matrix by row operations. The first column is not zero (
to the identity matrix by row operations. The first column is not zero (![]() is invertible); suppose the (1, 1)-entry
is invertible); suppose the (1, 1)-entry ![]() is not zero. Then row operations give
is not zero. Then row operations give
![Rendered by QuickLaTeX.com \begin{equation*} A = \left[ \begin{array}{ccc} a & b & c \\ d & e & f \\ g & h & i \end{array} \right] \rightarrow \left[ \begin{array}{ccc} a & b & c \\ ad & ae & af \\ ag & ah & ai \end{array} \right] \rightarrow \left[ \begin{array}{ccc} a & b & c \\ 0 & ae-bd & af-cd \\ 0 & ah-bg & ai-cg \end{array} \right] = \left[ \begin{array}{ccc} a & b & c \\ 0 & u & af-cd \\ 0 & v & ai-cg \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-50cea2b218d52fdeaf08693ba74ccfd9_l3.png)
where ![]() and
and ![]() . Since
. Since ![]() is invertible, one of
is invertible, one of ![]() and
and ![]() is nonzero (by Example 2.4.11); suppose that
is nonzero (by Example 2.4.11); suppose that ![]() . Then the reduction proceeds
. Then the reduction proceeds
![Rendered by QuickLaTeX.com \begin{equation*} A \rightarrow \left[ \begin{array}{ccc} a & b & c \\ 0 & u & af-cd \\ 0 & v & ai-cg \end{array} \right] \rightarrow \left[ \begin{array}{ccc} a & b & c \\ 0 & u & af-cd \\ 0 & uv & u(ai-cg) \end{array} \right] \rightarrow \left[ \begin{array}{ccc} a & b & c \\ 0 & u & af-cd \\ 0 & 0 & w \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-ddc3f89d05421ee8cde556d708acb9e3_l3.png)
where ![]() . We define
. We define
(3.1) ![]()
and observe that ![]() because
because ![]() (is invertible).
(is invertible).
To motivate the definition below, collect the terms in Equation 3.1 involving the entries ![]() ,
, ![]() , and
, and ![]() in row 1 of
in row 1 of ![]() :
:
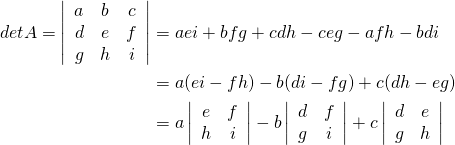
This last expression can be described as follows: To compute the determinant of a ![]() matrix
matrix ![]() , multiply each entry in row 1 by a sign times the determinant of the
, multiply each entry in row 1 by a sign times the determinant of the ![]() matrix obtained by deleting the row and column of that entry, and add the results. The signs alternate down row 1, starting with
matrix obtained by deleting the row and column of that entry, and add the results. The signs alternate down row 1, starting with ![]() . It is this observation that we generalize below.
. It is this observation that we generalize below.
Example 3.1.1
![Rendered by QuickLaTeX.com \begin{align*} \func{det}\left[ \begin{array}{rrr} 2 & 3 & 7 \\ -4 & 0 & 6 \\ 1 & 5 & 0 \end{array} \right] &= 2 \left| \begin{array}{rr} 0 & 6 \\ 5 & 0 \end{array} \right| - 3 \left| \begin{array}{rr} -4 & 6 \\ 1 & 0 \end{array} \right| + 7 \left| \begin{array}{rr} -4 & 0 \\ 1 & 5 \end{array} \right| \\ &= 2 (-30) - 3(-6) + 7(-20) \\ &= -182 \end{align*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-87046a3069e7d5c918c38b299d1c4f4b_l3.png)
This suggests an inductive method of defining the determinant of any square matrix in terms of determinants
of matrices one size smaller. The idea is to define determinants of ![]() matrices in terms of determinants of
matrices in terms of determinants of ![]() matrices,
matrices,
then we do ![]() matrices in terms of
matrices in terms of ![]() matrices, and so on.
matrices, and so on.
To describe this, we need some terminology.
Definition 3.1 Cofactors of a matrix
Assume that determinants of ![]() matrices have been defined. Given the
matrices have been defined. Given the ![]() matrix
matrix ![]() , let
, let
![]() denote the
denote the ![]() matrix obtained from A by deleting row
matrix obtained from A by deleting row ![]() and column
and column ![]()
Then the ![]() –cofactor
–cofactor ![]() is the scalar defined by
is the scalar defined by
![]()
Here ![]() is called the sign of the
is called the sign of the ![]() -position.
-position.
The sign of a position is clearly ![]() or
or ![]() , and the following diagram is useful for remembering it:
, and the following diagram is useful for remembering it:
![Rendered by QuickLaTeX.com \begin{equation*} \left[ \begin{array}{ccccc} + & - & + & - & \cdots \\ - & + & - & + & \cdots \\ + & - & + & - & \cdots \\ - & + & - & + & \cdots \\ \vdots & \vdots & \vdots & \vdots & \\ \end{array}\right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-02fde044ebcda50c3d89a77da647ab5d_l3.png)
Note that the signs alternate along each row and column with ![]() in the upper left corner.
in the upper left corner.
Example 3.1.2
![Rendered by QuickLaTeX.com \begin{equation*} A = \left[ \begin{array}{rrr} 3 & -1 & 6 \\ 5 & 2 & 7 \\ 8 & 9 & 4 \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-30402be55291c57fca345e158a54fdf4_l3.png)
Solution:
Here ![]() is the matrix
is the matrix ![]()
that remains when row ![]() and column
and column ![]() are deleted. The sign of position
are deleted. The sign of position ![]() is
is ![]() (this is also the
(this is also the ![]() -entry in the sign diagram), so the
-entry in the sign diagram), so the ![]() -cofactor is
-cofactor is
![]()
Turning to position ![]() , we find
, we find
![]()
Finally, the ![]() -cofactor is
-cofactor is
![]()
Clearly other cofactors can be found—there are nine in all, one for each position in the matrix.
We can now define ![]() for any square matrix
for any square matrix ![]()
Definition 3.2 Cofactor expansion of a Matrix
![]()
This is called the cofactor expansion of ![]() along row
along row ![]() .
.
It asserts that ![]() can be computed by multiplying the entries of row
can be computed by multiplying the entries of row ![]() by the corresponding
by the corresponding
cofactors, and adding the results. The astonishing thing is that ![]() can be computed by taking the cofactor expansion along
can be computed by taking the cofactor expansion along ![]() : Simply multiply each entry of that row or column by the corresponding cofactor and add.
: Simply multiply each entry of that row or column by the corresponding cofactor and add.
Theorem 3.1.1 Cofactor Expansion Theorem
of
Example 3.1.3
![Rendered by QuickLaTeX.com A = \left[ \begin{array}{rrr} 3 & 4 & 5 \\ 1 & 7 & 2 \\ 9 & 8 & -6 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f0b651f03a0031b6a5b0c6558f22de91_l3.png) .
.
Solution:
The cofactor expansion along the first row is as follows:
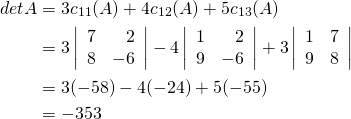
Note that the signs alternate along the row (indeed along ![]() row or column). Now we compute
row or column). Now we compute ![]() by expanding along the first column.
by expanding along the first column.
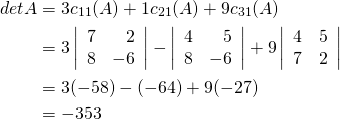
The reader is invited to verify that ![]() can be computed by expanding along any other row or column.
can be computed by expanding along any other row or column.
The fact that the cofactor expansion along ![]() of a matrix
of a matrix ![]() always gives the same result (the determinant of
always gives the same result (the determinant of ![]() ) is remarkable, to say the least. The choice of a particular row or column can simplify the calculation.
) is remarkable, to say the least. The choice of a particular row or column can simplify the calculation.
Example 3.1.4
![Rendered by QuickLaTeX.com A = \left[ \begin{array}{rrrr} 3 & 0 & 0 & 0 \\ 5 & 1 & 2 & 0 \\ 2 & 6 & 0 & -1 \\ -6 & 3 & 1 & 0 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5e0e469b38eea7ec5cad5a6fe4a37505_l3.png) .
.Solution:
The first choice we must make is which row or column to use in the
cofactor expansion. The expansion involves multiplying entries by
cofactors, so the work is minimized when the row or column contains as
many zero entries as possible. Row ![]() is a best choice in this matrix
is a best choice in this matrix
(column ![]() would do as well), and the expansion is
would do as well), and the expansion is
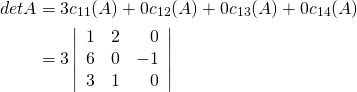
This is the first stage of the calculation, and we have succeeded in expressing the determinant of the ![]() matrix
matrix ![]()
in terms of the determinant of a ![]() matrix. The next stage involves
matrix. The next stage involves
this ![]() matrix. Again, we can use any row or column for the cofactor
matrix. Again, we can use any row or column for the cofactor
expansion. The third column is preferred (with two zeros), so
![Rendered by QuickLaTeX.com \begin{align*} \func{det } A &= 3 \left( 0 \left| \begin{array}{rr} 6 & 0 \\ 3 & 1 \end{array} \right| - (-1) \left| \begin{array}{rr} 1 & 2 \\ 3 & 1 \end{array} \right| + 0 \left| \begin{array}{rr} 1 & 2 \\ 6 & 0 \end{array} \right| \right) \\ &= 3 [ 0 + 1(-5) + 0] \\ &= -15 \end{align*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-b26c8547a26afad4010f65882973961c_l3.png)
This completes the calculation.
This example shows us that calculating a determinant is simplified a great deal when a row or column consists mostly of zeros. (In fact, when a row or column consists ![]() of zeros, the determinant is zero—simply expand along that row or column.) We did learn that one method of
of zeros, the determinant is zero—simply expand along that row or column.) We did learn that one method of ![]() zeros in a matrix is to apply elementary row operations to it. Hence, a natural question to ask is what effect such a row operation has on the determinant of the matrix. It turns out that the effect is easy to determine and that elementary
zeros in a matrix is to apply elementary row operations to it. Hence, a natural question to ask is what effect such a row operation has on the determinant of the matrix. It turns out that the effect is easy to determine and that elementary ![]() operations can be used in the same way. These observations lead to a technique for evaluating determinants that greatly reduces the labour involved. The necessary information is given in Theorem 3.1.2.
operations can be used in the same way. These observations lead to a technique for evaluating determinants that greatly reduces the labour involved. The necessary information is given in Theorem 3.1.2.
Theorem 3.1.2
Let ![]() denote an
denote an ![]() matrix.
matrix.
- If A has a row or column of zeros,
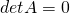 .
. - If two distinct rows (or columns) of
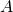 are interchanged, the determinant of the resulting matrix is
are interchanged, the determinant of the resulting matrix is 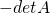 .
. - If a row (or column) of
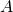 is multiplied by a constant
is multiplied by a constant 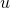 , the determinant of the resulting matrix is
, the determinant of the resulting matrix is 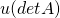 .
. - If two distinct rows (or columns) of
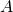 are identical,
are identical, 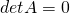 .
. - If a multiple of one row of
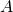 is added to a different row (or if a multiple of a column is added to a different column), the determinant of
is added to a different row (or if a multiple of a column is added to a different column), the determinant of
the resulting matrix is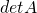 .
.
The following four examples illustrate how Theorem 3.1.2 is used to evaluate determinants.
Example 3.1.5
![Rendered by QuickLaTeX.com A = \left[ \begin{array}{rrr} 1 & -1 & 3 \\ 1 & 0 & -1 \\ 2 & 1 & 6 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-702ee1c1ca25a5973d2cca03feb3e27a_l3.png) .
.Solution:
The matrix does have zero entries, so expansion along (say) the second row would involve somewhat less work. However, a column operation can be
used to get a zero in position ![]() )—namely, add column 1 to column 3. Because this does not change the value of the determinant, we obtain
)—namely, add column 1 to column 3. Because this does not change the value of the determinant, we obtain
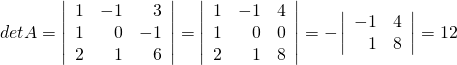
where we expanded the second ![]() matrix along row 2.
matrix along row 2.
Example 3.1.6
![Rendered by QuickLaTeX.com \func{det} \left[ \begin{array}{rrr} a & b & c \\ p & q & r \\ x & y & z \end{array} \right] = 6](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d1148f530243d419e0b4fff78528b5b3_l3.png) ,
,evaluate
![Rendered by QuickLaTeX.com A = \left[ \begin{array}{ccc} a+x & b+y & c+z \\ 3x & 3y & 3z \\ -p & -q & -r \end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-7973c49224181c1b69c8ea8dfdb76884_l3.png) .
.Solution:
First take common factors out of rows 2 and 3.
![Rendered by QuickLaTeX.com \begin{equation*} \func{det } A = 3(-1) \func{det} \left[ \begin{array}{ccc} a+x & b+y & c+z \\ x & y & z \\ p & q & r \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-7fa0844e5168a007e105b91c4fa487aa_l3.png)
Now subtract the second row from the first and interchange the last two rows.
![Rendered by QuickLaTeX.com \begin{equation*} \func{det } A = -3 \func{det} \left[ \begin{array}{ccc} a & b & c \\ x & y & z \\ p & q & r \end{array} \right] = 3 \func{det} \left[ \begin{array}{ccc} a & b & c \\ p & q & r \\ x & y & z \end{array} \right] = 3 \cdot 6 = 18 \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-576fad0e62a4b2f3490f9ec1a835de4e_l3.png)
The determinant of a matrix is a sum of products of its entries. In particular, if these entries are polynomials in ![]() , then the determinant itself is a polynomial in
, then the determinant itself is a polynomial in ![]() . It is often of interest to determine which values of
. It is often of interest to determine which values of ![]() make the determinant zero, so it is very useful if the determinant is given in factored form. Theorem 3.1.2 can help.
make the determinant zero, so it is very useful if the determinant is given in factored form. Theorem 3.1.2 can help.
Example 3.1.7
![Rendered by QuickLaTeX.com A = \left[ \begin{array}{ccc} 1 & x & x \\ x & 1 & x \\ x & x & 1 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-65e3ff4431339791b3965b318d112e2f_l3.png) .
.Solution:
To evaluate ![]() , first subtract
, first subtract ![]() times row 1 from rows 2 and 3.
times row 1 from rows 2 and 3.
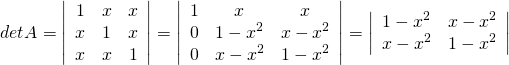
At this stage we could simply evaluate the determinant (the result is ![]() ). But then we would have to factor this polynomial to find the values of
). But then we would have to factor this polynomial to find the values of ![]() that make it zero. However, this factorization can be obtained directly by first factoring each entry in the determinant and taking a common
that make it zero. However, this factorization can be obtained directly by first factoring each entry in the determinant and taking a common
factor of ![]() from each row.
from each row.
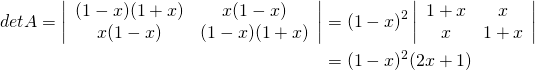
Hence, ![]() means
means ![]() , that is
, that is ![]() or
or ![]() .
.
Example 3.1.8
![Rendered by QuickLaTeX.com \begin{equation*} \func{det}\left[ \begin{array}{ccc} 1 & a_1 & a_1^2 \\ 1 & a_2 & a_2^2 \\ 1 & a_3 & a_3^2 \end{array} \right] = (a_3-a_1)(a_3-a_2)(a_2-a_1) \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-6773eb70015e72dc16e031a121a896c1_l3.png)
Solution:
Begin by subtracting row 1 from rows 2 and 3, and then expand along column 1:
![Rendered by QuickLaTeX.com \begin{equation*} \func{det} \left[ \begin{array}{ccc} 1 & a_1 & a_1^2 \\ 1 & a_2 & a_2^2 \\ 1 & a_3 & a_3^2 \end{array} \right] = \func{det} \left[ \begin{array}{ccc} 1 & a_1 & a_1^2 \\ 0 & a_2-a_1 & a_2^2-a_1^2 \\ 0 & a_3-a_1 & a_3^2-a_1^2 \end{array} \right] = \left[ \begin{array}{cc} a_2-a_1 & a_2^2-a_1^2 \\ a_3-a_1 & a_3^2-a_1^2 \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c769b04e2c14da00b0027fd367b8d2d0_l3.png)
Now ![]() and
and ![]() are common factors in rows 1 and 2, respectively, so
are common factors in rows 1 and 2, respectively, so
![Rendered by QuickLaTeX.com \begin{align*} \func{det} \left[ \begin{array}{ccc} 1 & a_1 & a_1^2 \\ 1 & a_2 & a_2^2 \\ 1 & a_3 & a_3^2 \end{array} \right] &= (a_2-a_1)(a_3-a_1)\func{det} \left[ \begin{array}{cc} 1& a_2+a_1 \\ 1 & a_3+a_1 \end{array} \right] \\ &= (a_2-a_1)(a_3-a_1)(a_3-a_2) \end{align*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-9e2a8c4b8a228d4cbd7558edf1fd7620_l3.png)
The matrix in Example 3.1.8 is called a Vandermonde matrix, and the formula for its determinant can be generalized to the ![]() case.
case.
If ![]() is an
is an ![]() matrix, forming
matrix, forming ![]() means multiplying
means multiplying ![]() row of
row of ![]() by
by ![]() . Applying property 3 of Theorem 3.1.2, we can take the common factor
. Applying property 3 of Theorem 3.1.2, we can take the common factor ![]() out of each row and so obtain the following useful result.
out of each row and so obtain the following useful result.
Theoerem 3.1.3
The next example displays a type of matrix whose determinant is easy to compute.
Example 3.1.9
![Rendered by QuickLaTeX.com A = \left[ \begin{array}{rrrr} a & 0 & 0 & 0 \\ u & b & 0 & 0 \\ v & w & c & 0 \\ x & y & z & d \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-9078ed7ad7f880137bc62414773558be_l3.png) .
.Solution:
Expand along row 1 to get 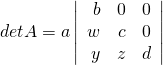 . Now expand this along the top row to get
. Now expand this along the top row to get ![]() , the product of the main diagonal entries.
, the product of the main diagonal entries.
A square matrix is called a ![]() if all entries above the main diagonal are zero (as in Example 3.1.9). Similarly, an
if all entries above the main diagonal are zero (as in Example 3.1.9). Similarly, an ![]() is one for which all entries below the main diagonal are zero. A
is one for which all entries below the main diagonal are zero. A ![]() is one that is either upper or lower triangular. Theorem 3.1.4 gives an easy rule for calculating the determinant of any triangular matrix.
is one that is either upper or lower triangular. Theorem 3.1.4 gives an easy rule for calculating the determinant of any triangular matrix.
Theorem 3.1.4
Theorem 3.1.4 is useful in computer calculations because it is a routine matter to carry a matrix to triangular form using row operations.
3.2 Determinants and Matrix Inverses
In this section, several theorems about determinants are derived. One consequence of these theorems is that a square matrix ![]() is invertible if and only if
is invertible if and only if ![]() . Moreover, determinants are used to give a formula for
. Moreover, determinants are used to give a formula for ![]() which, in turn, yields a formula (called Cramer’s rule) for the
which, in turn, yields a formula (called Cramer’s rule) for the
solution of any system of linear equations with an invertible coefficient matrix.
We begin with a remarkable theorem (due to Cauchy in 1812) about the determinant of a product of matrices.
Theorem 3.2.1 Product Theorem
The complexity of matrix multiplication makes the product theorem quite unexpected. Here is an example where it reveals an important numerical identity.
Example 3.2.1
If ![]() and
and ![]()
then ![]() .
.
Hence ![]() gives the identity
gives the identity
![]()
Theorem 3.2.1 extends easily to ![]() . In fact, induction gives
. In fact, induction gives
![]()
for any square matrices ![]() of the same size. In particular, if each
of the same size. In particular, if each ![]() , we obtain
, we obtain
![]()
We can now give the invertibility condition.
Theorem 3.2.2
Proof:
If ![]() is invertible, then
is invertible, then ![]() ; so the product theorem gives
; so the product theorem gives
![]()
Hence, ![]() and also
and also ![]() .
.
Conversely, if ![]() , we show that
, we show that ![]() can be carried to
can be carried to ![]() by elementary row operations (and invoke Theorem 2.4.5). Certainly,
by elementary row operations (and invoke Theorem 2.4.5). Certainly, ![]() can be carried to its reduced row-echelon form
can be carried to its reduced row-echelon form ![]() , so
, so ![]() where the
where the ![]() are elementary matrices (Theorem 2.5.1). Hence the product theorem gives
are elementary matrices (Theorem 2.5.1). Hence the product theorem gives
![]()
Since ![]() for all elementary matrices
for all elementary matrices ![]() , this shows
, this shows ![]() . In particular,
. In particular, ![]() has no row of zeros, so
has no row of zeros, so ![]() because
because ![]() is square and reduced row-echelon. This is what we wanted.
is square and reduced row-echelon. This is what we wanted.
Example 3.2.2
![Rendered by QuickLaTeX.com A = \left[ \begin{array}{rcr} 1 & 0 & -c \\ -1 & 3 & 1 \\ 0 & 2c & -4 \end{array} \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d8f3a6066df0f7650304bb29c179781d_l3.png)
have an inverse?
Solution:
Compute ![]() by first adding
by first adding ![]() times column 1 to column 3 and then expanding along row 1.
times column 1 to column 3 and then expanding along row 1.
![Rendered by QuickLaTeX.com \begin{equation*} \func{det } A = \func{det} \left[ \begin{array}{rcr} 1 & 0 & -c \\ -1 & 3 & 1 \\ 0 & 2c & -4 \end{array} \right] = \func{det} \left[ \begin{array}{rcc} 1 & 0 & 0 \\ -1 & 3 & 1-c \\ 0 & 2c & -4 \end{array} \right] = 2(c+2)(c-3) \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-26664917142081574465df4d6114d430_l3.png)
Hence, ![]() if
if ![]() or
or ![]() , and
, and ![]() has an inverse if
has an inverse if ![]() and
and ![]() .
.
Example 3.2.3
Solution:
We have ![]() by the product theorem, and
by the product theorem, and ![]() by Theorem 3.2.2 because
by Theorem 3.2.2 because ![]() is invertible. Hence
is invertible. Hence
![]()
so ![]() for each
for each ![]() . This shows that each
. This shows that each ![]() is invertible, again by Theorem 3.2.2.
is invertible, again by Theorem 3.2.2.
Theorem 3.2.3
Proof:
Consider first the case of an elementary matrix ![]() . If
. If ![]() is of type I or II, then
is of type I or II, then ![]() ; so certainly
; so certainly ![]() . If
. If ![]() is of type III, then
is of type III, then ![]() is also of type III; so
is also of type III; so ![]() by Theorem 3.1.2. Hence,
by Theorem 3.1.2. Hence, ![]() for every elementary matrix
for every elementary matrix ![]() .
.
Now let ![]() be any square matrix. If
be any square matrix. If ![]() is not invertible, then neither is
is not invertible, then neither is ![]() ; so
; so ![]() by Theorem 3.1.2. On the other hand, if
by Theorem 3.1.2. On the other hand, if ![]() is invertible, then
is invertible, then ![]() , where the
, where the ![]() are elementary matrices (Theorem 2.5.2). Hence,
are elementary matrices (Theorem 2.5.2). Hence, ![]() so the product theorem gives
so the product theorem gives

This completes the proof.
Example 3.2.4
Solution:
We use several of the facts just derived.
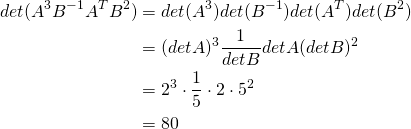
Example 3.2.5
Solution:
If ![]() is orthogonal, we have
is orthogonal, we have ![]() . Take determinants to obtain
. Take determinants to obtain
![]()
Since ![]() is a number, this means
is a number, this means ![]() .
.
Adjugates
In Section 2.4 we defined the adjugate of a 2 ![]() 2 matrix
2 matrix ![]()
to be ![]() .
.
Then we verified that ![]() and hence that, if
and hence that, if ![]() ,
, ![]() . We are now able to define the adjugate of an arbitrary square matrix and to show that this formula for the inverse remains valid (when the
. We are now able to define the adjugate of an arbitrary square matrix and to show that this formula for the inverse remains valid (when the
inverse exists).
Recall that the ![]() -cofactor
-cofactor ![]() of a square matrix
of a square matrix ![]() is a number defined for each position
is a number defined for each position ![]() in the matrix. If
in the matrix. If ![]() is a square matrix, the
is a square matrix, the ![]()
![]() is defined to be the matrix
is defined to be the matrix ![]() whose
whose ![]() -entry is the
-entry is the ![]() -cofactor of
-cofactor of ![]() .
.
Definition 3.3 Adjugate of a Matrix
![]()
Example 3.2.6
![Rendered by QuickLaTeX.com A = \left[ \begin{array}{rrr} 1 & 3 & -2 \\ 0 & 1 & 5 \\ -2 & -6 & 7 \end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-4258fcb7af176257fa2d662ab64927f4_l3.png)
and calculate
Solution:
We first find the cofactor matrix.
![Rendered by QuickLaTeX.com \begin{align*} \left[ \begin{array}{rrr} c_{11}(A) & c_{12}(A) & c_{13}(A) \\ c_{21}(A) & c_{22}(A) & c_{23}(A) \\ c_{31}(A) & c_{32}(A) & c_{33}(A) \end{array}\right] &= \left[ \begin{array}{ccc} \left| \begin{array}{rr} 1 & 5 \\ -6 & 7 \end{array}\right| & -\left| \begin{array}{rr} 0 & 5 \\ -2 & 7 \end{array}\right| & \left| \begin{array}{rr} 0 & 1 \\ -2 & -6 \end{array}\right| \\ & & \\ -\left| \begin{array}{rr} 3 & -2 \\ -6 & 7 \end{array}\right| & \left| \begin{array}{rr} 1 & -2 \\ -2 & 7 \end{array}\right| & -\left| \begin{array}{rr} 1 & 3 \\ -2 & -6 \end{array}\right| \\ & & \\ \left| \begin{array}{rr} 3 & -2 \\ 1 & 5 \end{array}\right| & -\left| \begin{array}{rr} 1 & -2 \\ 0 & 5 \end{array}\right| & \left| \begin{array}{rr} 1 & 3 \\ 0 & 1 \end{array}\right| \end{array}\right] \\ &= \left[ \begin{array}{rrr} 37 & -10 & 2 \\ -9 & 3 & 0 \\ 17 & -5 & 1 \end{array}\right] \end{align*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-8cdbd72baf5602209280cd9d75004146_l3.png)
Then the adjugate of ![]() is the transpose of this cofactor matrix.
is the transpose of this cofactor matrix.
![Rendered by QuickLaTeX.com \begin{equation*} \func{adj } A = \left[ \begin{array}{rrr} 37 & -10 & 2 \\ -9 & 3 & 0 \\ 17 & -5 & 1 \end{array}\right] ^T = \left[ \begin{array}{rrr} 37 & -9 & 17 \\ -10 & 3 & -5 \\ 2 & 0 & 1 \end{array}\right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-192ad4b9e6f537f995ba38b588226103_l3.png)
The computation of ![]() gives
gives
![Rendered by QuickLaTeX.com \begin{equation*} A(\func{adj } A) = \left[ \begin{array}{rrr} 1 & 3 & -2 \\ 0 & 1 & 5 \\ -2 & -6 & 7 \end{array}\right] \left[ \begin{array}{rrr} 37 & -9 & 17 \\ -10 & 3 & -5 \\ 2 & 0 & 1 \end{array}\right] = \left[ \begin{array}{rrr} 3 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 3 \end{array}\right] = 3I \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-e418d798d3941852b81baa14705a6b98_l3.png)
and the reader can verify that also ![]() . Hence, analogy with the
. Hence, analogy with the ![]() case would indicate that
case would indicate that ![]() ; this is, in fact, the case.
; this is, in fact, the case.
The relationship ![]() holds for any square matrix
holds for any square matrix ![]() .
.
Theorem 3.2.4 Adjugate formula
![]()
In particular, if det A ![]() 0, the inverse of A is given by
0, the inverse of A is given by
![]()
It is important to note that this theorem is ![]() an efficient way to find the inverse of the matrix
an efficient way to find the inverse of the matrix ![]() . For example, if
. For example, if ![]() were
were ![]() , the calculation of
, the calculation of ![]() would require computing
would require computing ![]() determinants of
determinants of ![]() matrices! On the other hand, the matrix inversion algorithm would find
matrices! On the other hand, the matrix inversion algorithm would find ![]() with about the same effort as finding
with about the same effort as finding ![]() . Clearly, Theorem 3.2.4 is not a
. Clearly, Theorem 3.2.4 is not a ![]() result: its virtue is that it gives a formula for
result: its virtue is that it gives a formula for ![]() that is useful for
that is useful for ![]() purposes.
purposes.
Example 3.2.7
![Rendered by QuickLaTeX.com A = \left[ \begin{array}{rrr} 2 & 1 & 3 \\ 5 & -7 & 1 \\ 3 & 0 & -6 \end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-57f42868acde57d98a6afc6f0a7b22ee_l3.png) .
.Solution:
First compute
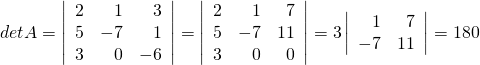
Since ![]() ,
,
the ![]() -entry of
-entry of ![]() is the
is the ![]() -entry of the matrix
-entry of the matrix ![]() ; that is, it equals
; that is, it equals
![]()
Example 3.2.8
Solution:
Write ![]() ; we must show that
; we must show that ![]() . We have
. We have ![]() by Theorem 3.2.4, so taking determinants gives
by Theorem 3.2.4, so taking determinants gives ![]() . Hence we are done if
. Hence we are done if ![]() . Assume
. Assume ![]() ; we must show that
; we must show that ![]() , that is,
, that is, ![]() is not invertible. If
is not invertible. If ![]() , this follows from
, this follows from ![]() ; if
; if ![]() , it follows because then
, it follows because then ![]() .
.
Cramer’s Rule
Theorem 3.2.4 has a nice application to linear equations. Suppose
![]()
is a system of ![]() equations in
equations in ![]() variables
variables ![]() . Here
. Here ![]() is the
is the ![]() coefficient matrix and
coefficient matrix and ![]() and
and ![]() are the columns
are the columns
![Rendered by QuickLaTeX.com \begin{equation*} \vec{x} = \left[ \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right] \mbox{ and } \vec{b} = \left[ \begin{array}{c} b_1 \\ b_2 \\ \vdots \\ b_n \end{array} \right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-bd3ae265a30ec3606c1ebecd2def7006_l3.png)
of variables and constants, respectively. If ![]() , we left multiply by
, we left multiply by ![]() to obtain the solution
to obtain the solution ![]() . When we use the adjugate formula, this becomes
. When we use the adjugate formula, this becomes
![Rendered by QuickLaTeX.com \begin{align*} \left[ \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right] &= \frac{1}{\func{det } A} (\func{adj } A)\vec{b} \\ &= \frac{1}{\func{det } A} \left[ \begin{array}{cccc} c_{11}(A) & c_{21}(A) & \cdots & c_{n1}(A) \\ c_{12}(A) & c_{22}(A) & \cdots & c_{n2}(A) \\ \vdots & \vdots & & \vdots \\ c_{1n}(A) & c_{2n}(A) & \cdots & c_{nn}(A) \end{array}\right] \left[ \begin{array}{c} b_1 \\ b_2 \\ \vdots \\ b_n \end{array} \right] \end{align*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-4e30033c6c6910ed55cb742561e6254c_l3.png)
Hence, the variables ![]() are given by
are given by
![Rendered by QuickLaTeX.com \begin{align*} x_1 &= \frac{1}{\func{det } A} \left[ b_1c_{11}(A) + b_2c_{21}(A) + \cdots + b_nc_{n1}(A)\right]\\ x_2 &= \frac{1}{\func{det } A} \left[ b_1c_{12}(A) + b_2c_{22}(A) + \cdots + b_nc_{n2}(A)\right] \\ & \hspace{5em} \vdots \hspace{5em} \vdots\\ x_n &= \frac{1}{\func{det } A} \left[ b_1c_{1n}(A) + b_2c_{2n}(A) + \cdots + b_nc_{nn}(A)\right] \end{align*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-58f60682aa70b1b63b523731b0819dc5_l3.png)
Now the quantity ![]() occurring in the formula for
occurring in the formula for ![]() looks like the cofactor expansion of the determinant of a matrix. The cofactors involved are
looks like the cofactor expansion of the determinant of a matrix. The cofactors involved are ![]() , corresponding to the first column of
, corresponding to the first column of ![]() . If
. If ![]() is obtained from
is obtained from ![]() by replacing the first column of
by replacing the first column of ![]() by
by ![]() , then
, then ![]() for each
for each ![]() because column
because column ![]() is deleted when computing them. Hence, expanding
is deleted when computing them. Hence, expanding ![]() by the first column gives
by the first column gives
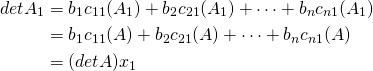
Hence, ![]() and similar results hold for the other variables.
and similar results hold for the other variables.
Theorem 3.2.5 Cramer’s Rule
![]()
of ![]() equations in the variables
equations in the variables ![]() is given by
is given by
![]()
where, for each ![]() ,
, ![]() is the matrix obtained from
is the matrix obtained from ![]() by replacing column
by replacing column ![]() by
by ![]() .
.
Example 3.2.9
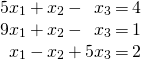
Solution:
Compute the determinants of the coefficient matrix ![]() and the matrix
and the matrix ![]() obtained from it by replacing the first column by the column of constants.
obtained from it by replacing the first column by the column of constants.
![Rendered by QuickLaTeX.com \begin{align*} \func{det } A &= \func{det} \left[ \begin{array}{rrr} 5 & 1 & -1 \\ 9 & 1 & -1 \\ 1 & -1 & 5 \end{array}\right] = -16 \\ \func{det } A_1 &= \func{det} \left[ \begin{array}{rrr} 4 & 1 & -1 \\ 1 & 1 & -1 \\ 2 & -1 & 5 \end{array}\right] = 12 \end{align*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-2ac63bd51306debfc59a1bc1c58cf0d5_l3.png)
Hence, ![]() by Cramer’s rule.
by Cramer’s rule.
Cramer’s rule is ![]() an efficient way to solve linear systems or invert matrices. True, it enabled us to calculate
an efficient way to solve linear systems or invert matrices. True, it enabled us to calculate ![]() here without computing
here without computing ![]() or
or ![]() . Although this might seem an advantage, the truth of the matter is that, for large systems of equations, the number of computations needed to find
. Although this might seem an advantage, the truth of the matter is that, for large systems of equations, the number of computations needed to find ![]() the variables by the gaussian algorithm is comparable to the number required to find
the variables by the gaussian algorithm is comparable to the number required to find ![]() of the determinants involved in Cramer’s rule. Furthermore, the algorithm works when the matrix of the system is not invertible and even when the coefficient matrix is not square. Like the adjugate formula, then, Cramer’s rule is
of the determinants involved in Cramer’s rule. Furthermore, the algorithm works when the matrix of the system is not invertible and even when the coefficient matrix is not square. Like the adjugate formula, then, Cramer’s rule is ![]() a practical numerical technique; its virtue is theoretical.
a practical numerical technique; its virtue is theoretical.
3.3 Diagonalization and Eigenvalues
The world is filled with examples of systems that evolve in time—the weather in a region, the economy of a nation, the diversity of an ecosystem, etc. Describing such systems is difficult in general and various methods have been developed in special cases. In this section we describe one such method, called ![]() which is one of the most important techniques in linear algebra. A very fertile example of this procedure is in modelling the growth of the population of an animal species. This has attracted more attention in recent years with the ever increasing awareness that many species are endangered. To motivate the technique, we begin by setting up a simple model of a bird population in which we make assumptions about survival and reproduction rates.
which is one of the most important techniques in linear algebra. A very fertile example of this procedure is in modelling the growth of the population of an animal species. This has attracted more attention in recent years with the ever increasing awareness that many species are endangered. To motivate the technique, we begin by setting up a simple model of a bird population in which we make assumptions about survival and reproduction rates.
Example 3.3.1
Consider the evolution of the population of a species of birds. Because the number of males and females are nearly equal, we count only females. We assume that each female remains a juvenile for one year and then becomes an adult, and that only adults have offspring. We make three assumptions about reproduction and survival rates:
- The number of juvenile females hatched in any year is twice the number of adult females alive the year before (we say the
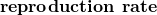 is 2).
is 2). - Half of the adult females in any year survive to the next year (the
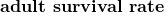 is
is 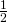 ).
). - One-quarter of the juvenile females in any year survive into adulthood (the
 is
is 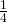 ).
).
If there were 100 adult females and 40 juvenile females alive initially, compute the population of females ![]() years later.
years later.
Solution:
Let ![]() and
and ![]() denote, respectively, the number of adult and juvenile females after
denote, respectively, the number of adult and juvenile females after ![]() years, so that the total female population is the sum
years, so that the total female population is the sum ![]() . Assumption 1 shows that
. Assumption 1 shows that ![]() , while assumptions 2 and 3 show that
, while assumptions 2 and 3 show that ![]() . Hence the numbers
. Hence the numbers ![]() and
and ![]() in successive years are related by the following equations:
in successive years are related by the following equations:
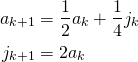
If we write ![]()
and ![]()
these equations take the matrix form
![]()
Taking ![]() gives
gives ![]() , then taking
, then taking ![]() gives
gives ![]() , and taking
, and taking ![]() gives
gives ![]() . Continuing in this way, we get
. Continuing in this way, we get
![]()
Since ![]()
is known, finding the population profile ![]() amounts to computing
amounts to computing ![]() for all
for all ![]() . We will complete this calculation in Example 3.3.12 after some new techniques have been developed.
. We will complete this calculation in Example 3.3.12 after some new techniques have been developed.
Let ![]() be a fixed
be a fixed ![]() matrix. A sequence
matrix. A sequence ![]() of column vectors in
of column vectors in ![]() is called a
is called a ![]() . Many models regard
. Many models regard ![]() as a continuous function of the time
as a continuous function of the time ![]() , and replace our condition between
, and replace our condition between ![]() and
and ![]() with a differential relationship viewed as functions of time if
with a differential relationship viewed as functions of time if ![]() is known and the other
is known and the other ![]() are determined (as in Example 3.3.1) by the conditions
are determined (as in Example 3.3.1) by the conditions
![]()
These conditions are called a ![]() for the vectors
for the vectors ![]() . As in Example 3.3.1, they imply that
. As in Example 3.3.1, they imply that
![]()
so finding the columns ![]() amounts to calculating
amounts to calculating ![]() for
for ![]() .
.
Direct computation of the powers ![]() of a square matrix
of a square matrix ![]() can be time-consuming, so we adopt an indirect method that is commonly used. The idea is to first
can be time-consuming, so we adopt an indirect method that is commonly used. The idea is to first ![]() the matrix
the matrix ![]() , that is, to find an invertible matrix
, that is, to find an invertible matrix ![]() such that
such that
(3.8) ![]()
This works because the powers ![]() of the diagonal matrix
of the diagonal matrix ![]() are easy to compute, and Equation (3.8) enables us to compute powers
are easy to compute, and Equation (3.8) enables us to compute powers ![]() of the matrix
of the matrix ![]() in terms of powers
in terms of powers ![]() of
of ![]() . Indeed, we can solve Equation (3.8) for
. Indeed, we can solve Equation (3.8) for ![]() to get
to get ![]() . Squaring this gives
. Squaring this gives
![]()
Using this we can compute ![]() as follows:
as follows:
![]()
Continuing in this way we obtain Theorem 3.3.1 (even if ![]() is not diagonal).
is not diagonal).
Theorem 3.3.1
Hence computing ![]() comes down to finding an invertible matrix
comes down to finding an invertible matrix ![]() as in equation Equation (3.8). To do this it is necessary to first compute certain numbers (called eigenvalues) associated with the matrix
as in equation Equation (3.8). To do this it is necessary to first compute certain numbers (called eigenvalues) associated with the matrix ![]() .
.
Eigenvalue and Eigenvectors
Definition 3.4 Eigenvalues and Eigenvectors of a Matrix
![]()
In this case, ![]() is called an
is called an ![]() of
of ![]() corresponding to the eigenvalue
corresponding to the eigenvalue ![]() , or a
, or a ![]() –
–![]() for short.
for short.
Example 3.3.2
The matrix ![]() in Example 3.3.2 has another eigenvalue in addition to
in Example 3.3.2 has another eigenvalue in addition to ![]() . To find it, we develop a general procedure for
. To find it, we develop a general procedure for ![]()
![]() matrix
matrix ![]() .
.
By definition a number ![]() is an eigenvalue of the
is an eigenvalue of the ![]() matrix
matrix ![]() if and only if
if and only if ![]() for some column
for some column ![]() . This is equivalent to asking that the homogeneous system
. This is equivalent to asking that the homogeneous system
![]()
of linear equations has a nontrivial solution ![]() . By Theorem 2.4.5 this happens if and only if the matrix
. By Theorem 2.4.5 this happens if and only if the matrix ![]() is not invertible and this, in turn, holds if and only if the determinant of the coefficient matrix is zero:
is not invertible and this, in turn, holds if and only if the determinant of the coefficient matrix is zero:
![]()
This last condition prompts the following definition:
Definition 3.5 Characteristic Polynomial of a Matrix
![]()
Note that ![]() is indeed a polynomial in the variable
is indeed a polynomial in the variable ![]() , and it has degree
, and it has degree ![]() when
when ![]() is an
is an ![]() matrix (this is illustrated in the examples below). The above discussion shows that a number
matrix (this is illustrated in the examples below). The above discussion shows that a number ![]() is an eigenvalue of
is an eigenvalue of ![]() if and only if
if and only if ![]() , that is if and only if
, that is if and only if ![]() is a
is a ![]() of the characteristic polynomial
of the characteristic polynomial ![]() . We record these observations in
. We record these observations in
Theorem 3.3.2
Let ![]() be an
be an ![]() matrix.
matrix.
- The eigenvalues
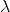 of
of 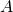 are the roots of the characteristic polynomial
are the roots of the characteristic polynomial 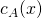 of
of 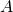 .
. - The
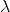 -eigenvectors
-eigenvectors 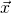 are the nonzero solutions to the homogeneous system
are the nonzero solutions to the homogeneous system
![]()
of linear equations with ![]() as coefficient matrix.
as coefficient matrix.
In practice, solving the equations in part 2 of Theorem 3.3.2 is a routine application of gaussian elimination, but finding the eigenvalues can be difficult, often requiring computers. For now, the examples and exercises will be constructed so that the roots of the characteristic polynomials are relatively easy to find
(usually integers). However, the reader should not be misled by this into thinking that eigenvalues are so easily obtained for the matrices that occur in practical applications!
Example 3.3.3
discussed in Example 3.3.2, and then find all the eigenvalues and their eigenvectors.
Solution:
Since ![]()
we get
![]()
Hence, the roots of ![]() are
are ![]() and
and ![]() , so these are the eigenvalues of
, so these are the eigenvalues of ![]() . Note that
. Note that ![]() was the eigenvalue mentioned in Example 3.3.2, but we have found a new one:
was the eigenvalue mentioned in Example 3.3.2, but we have found a new one: ![]() .
.
To find the eigenvectors corresponding to ![]() , observe that in this case
, observe that in this case
![]()
so the general solution to ![]() is
is ![]()
where ![]() is an arbitrary real number. Hence, the eigenvectors
is an arbitrary real number. Hence, the eigenvectors ![]() corresponding to
corresponding to ![]() are
are ![]() where
where ![]() is arbitrary. Similarly,
is arbitrary. Similarly, ![]() gives rise to the eigenvectors
gives rise to the eigenvectors ![]() which includes the observation in Example 3.3.2.
which includes the observation in Example 3.3.2.
Note that a square matrix ![]() has
has ![]() eigenvectors associated with any given eigenvalue
eigenvectors associated with any given eigenvalue ![]() . In fact
. In fact ![]() nonzero solution
nonzero solution ![]() of
of ![]() is an eigenvector. Recall that these solutions are all linear combinations of certain basic solutions determined by the gaussian algorithm (see Theorem 1.3.2). Observe that any nonzero multiple of an eigenvector is again an eigenvector, and such multiples are often more convenient. Any set of nonzero multiples of the basic solutions of
is an eigenvector. Recall that these solutions are all linear combinations of certain basic solutions determined by the gaussian algorithm (see Theorem 1.3.2). Observe that any nonzero multiple of an eigenvector is again an eigenvector, and such multiples are often more convenient. Any set of nonzero multiples of the basic solutions of ![]() will be called a set of basic eigenvectors corresponding to
will be called a set of basic eigenvectors corresponding to ![]() .
.
GeoGebra Exercise: Eigenvalue and eigenvectors
https://www.geogebra.org/m/DJXTtm2k
Please answer these questions after you open the webpage:
1. Set the matrix to be
![]()
2. Drag the point ![]() until you see the vector
until you see the vector ![]() and
and ![]() are on the same line. Record the value of
are on the same line. Record the value of ![]() . How many times do you see
. How many times do you see ![]() and
and ![]() lying on the same line when
lying on the same line when ![]() travel through the whole circle? Why?
travel through the whole circle? Why?
3. Based on your observation, what can we say about the eigenvalue and eigenvector of ![]() ?
?
4. Set the matrix to be
![]()
and repeat what you did above.
5. Check your lecture notes about the eigenvalues and eigenvectors of this matrix. Are the results consistent with what you observe?
Example 3.3.4:
Find the characteristic polynomial, eigenvalues, and basic eigenvectors for
![Rendered by QuickLaTeX.com \begin{equation*} A = \left[ \begin{array}{rrr} 2 & 0 & 0 \\ 1 & 2 & -1 \\ 1 & 3 & -2 \end{array}\right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-53272e1c335df6877d01266398602405_l3.png)
Solution:
Here the characteristic polynomial is given by
![Rendered by QuickLaTeX.com \begin{equation*} c_A(x) = \func{det} \left[ \begin{array}{ccc} x-2 & 0 & 0 \\ -1 & x-2 & 1 \\ -1 & -3 & x+2 \end{array}\right] = (x-2)(x-1)(x+1) \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-4baa448b69c309a3a34458eea4ff8467_l3.png)
so the eigenvalues are ![]() ,
, ![]() , and
, and ![]() . To find all eigenvectors for
. To find all eigenvectors for ![]() , compute
, compute
![Rendered by QuickLaTeX.com \begin{equation*} \lambda_1 I-A = \left[ \begin{array}{ccc} \lambda_1-2 & 0 & 0 \\ -1 & \lambda_1-2 & 1 \\ -1 & -3 & \lambda_1+2 \end{array}\right] = \left[ \begin{array}{rrr} 0 & 0 & 0 \\ -1 & 0 & 1 \\ -1 & -3 & 4 \end{array}\right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5494265f515c5b384d6205d9f2d6d0e8_l3.png)
We want the (nonzero) solutions to ![]() . The augmented matrix becomes
. The augmented matrix becomes
![Rendered by QuickLaTeX.com \begin{equation*} \left[ \begin{array}{rrr|r} 0 & 0 & 0 & 0 \\ -1 & 0 & 1 & 0 \\ -1 & -3 & 4 & 0 \end{array}\right] \rightarrow \left[ \begin{array}{rrr|r} 1 & 0 & -1 & 0 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right] \end{equation*}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-03ed8d762c4f083e44de0344e1642ac0_l3.png)
using row operations. Hence, the general solution ![]() to
to ![]() is
is ![Rendered by QuickLaTeX.com \vec{x} = t \left[ \begin{array}{r} 1 \\ 1 \\ 1 \end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-2e1ae3ddf1c671db9f5a46fb5783f5a3_l3.png)
where ![]() is arbitrary, so we can use
is arbitrary, so we can use ![Rendered by QuickLaTeX.com \vec{x}_1 = \left[ \begin{array}{r} 1 \\ 1 \\ 1 \end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-af0b8b4a951233bcb857ed465446ade0_l3.png)
as the basic eigenvector corresponding to ![]() . As the reader can verify, the gaussian algorithm gives basic eigenvectors
. As the reader can verify, the gaussian algorithm gives basic eigenvectors ![Rendered by QuickLaTeX.com \vec{x}_2 = \left[ \begin{array}{r} 0 \\ 1 \\ 1 \end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c8a51c6c85f6cf119f31d1b5642e04f5_l3.png)
and ![Rendered by QuickLaTeX.com \vec{x}_3 = \left[ \begin{array}{r} 0 \\ \frac{1}{3} \\ 1 \end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-3423d147914a0e1ffec189d398bffe18_l3.png)
corresponding to ![]() and
and ![]() , respectively. Note that to eliminate fractions, we could instead use
, respectively. Note that to eliminate fractions, we could instead use ![Rendered by QuickLaTeX.com 3\vec{x}_3 = \left[ \begin{array}{r} 0 \\ 1 \\ 3 \end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-7e3d46fe19caf7168c05379a62e0d72f_l3.png)
as the basic ![]() -eigenvector.
-eigenvector.
Example 3.3.5
If ![]() is a square matrix, show that
is a square matrix, show that ![]() and
and ![]() have the same characteristic polynomial, and hence the same eigenvalues.
have the same characteristic polynomial, and hence the same eigenvalues.
Solution:
We use the fact that ![]() . Then
. Then
![]()
by Theorem 3.2.3. Hence ![]() and
and ![]() have the same roots, and so
have the same roots, and so ![]() and
and ![]() have the same eigenvalues (by Theorem 3.3.2).
have the same eigenvalues (by Theorem 3.3.2).
The eigenvalues of a matrix need not be distinct. For example, if ![]()
the characteristic polynomial is ![]() so the eigenvalue 1 occurs twice. Furthermore, eigenvalues are usually not computed as the roots of the characteristic polynomial. There are iterative, numerical methods that are much more efficient for large matrices.
so the eigenvalue 1 occurs twice. Furthermore, eigenvalues are usually not computed as the roots of the characteristic polynomial. There are iterative, numerical methods that are much more efficient for large matrices.

