2.7 Deferred Annuities

Margaret Dancy

2.7 Deferred Annuities

Learning Objectives

Solve problems involving a deferred annuity

Formula & Symbol Hub

Symbols Used

$F V$ = Future value or maturity value
$P V$ = Present value of principal
$P M T$ = Annuity payment amount
$I / Y$ = Nominal interest rate
$P / Y$ = Number of payments per year or payment frequency
$C / Y$ = Number of compounds per year or compounding frequency
$n$ or $N$ = Total number of annuity payments

Formulas Used

Formula 2.1 – Total Number of Payments (Annuity)

$n = P / Y \times t$

Formula 2.2 – Future Value of Ordinary Annuity

$F V = P M T \times [\frac{(1 + i_{2})^{n} - 1}{i_{2}}]$

Formula 2.3 – Future Value of Annuity Due

$F V = P M T \times (1 + i_{2}) \times [\frac{(1 + i_{2})^{n} - 1}{i_{2}}]$

Formula 2.4 – Present Value of Ordinary Annuity

$P V = P M T \times [\frac{1 - (1 + i_{2})^{- n}}{i_{2}}]$

Formula 2.5 – Present Value of Annuity Due

$P V = P M T \times (1 + i_{2}) \times [\frac{1 - (1 + i_{2})^{- n}}{i_{2}}]$

Introduction

Suppose at the age of $21$ , you took $$ 50, 000$ and invested it into an RRSP. You leave the money in the RRSP and do not make any further contributions to the RRSP. When you retire in $40$ years, you will take the accumulated money in the RRSP to provide you with monthly payments for $20$ years during your retirement. During the $40$ years leading up to your retirement, the $$ 50, 000$ you invested at age $21$ is left to earn interest, with no payments or withdrawals occurring during that time. The payments begin after this $40$ year period of interest. This is an example of a deferred annuity, where the payments begin after an extended period of time.

What is a Deferred Annuity?

Adeferred annuity is a financial transaction where annuity payments are delayed until a certain period of time has elapsed. Usually the annuity has two stages, as depicted in this figure.

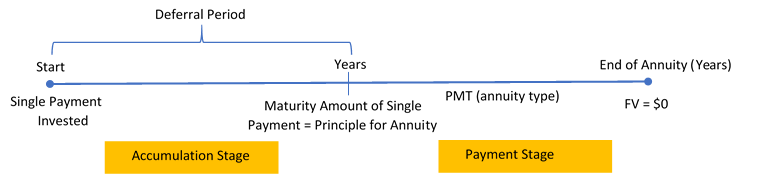
Timeline showing a Single Payment Invested at Start and a Deferral Period (Accummulation Stage) from Start to Years. At Years, Maturity Amount of Single Payment = Principal of Annuity. From Years to End of Annuity (Years), Payment Stage with PMT (annuity type). At End of Annuity (Years), FV = $0 — Figure 2.7.1

Accumulation Stage: A single payment is allowed to earn interest for a specified duration. There are no annuity payments during this period of time, which is commonly referred to as theperiod of deferral.
Payment Stage: The annuity takes the form of any of the four annuity types and starts at the beginning of this stage as per the financial contract. Note that the maturity value of the accumulation stage is the same as the principal for the payments stage.

Working with Deferred Annuities

For deferred annuities, the most common unknown variables are either the present value, the length of the period of deferral, the annuity payment amount, or the number of annuity payments that are sustainable for a fixed income payment. Follow this sequence of steps for each of these variables.

Solving for the Present Value

Solving for the Period of Deferral

Solving for the Annuity Payment

Solving for the Number of Annuity Payments

Step 1

Draw a timeline. Identify the known quantities. Identify the locations of the present value of the annuity and the first payment and place the corresponding times on the timeline.

Step 2

Starting at the end of your timeline, calculate the present value of the annuity.

Starting at the beginning of the timeline, calculate the future value at the end of the period of deferral.

Step 3

Calculate the present value at the start of the period of deferral.

Calculate the number of compounding periods and convert to years and months.

Calculate the annuity payment.

Calculate the number of annuity payments and convert to years and months.

Things to Watch Out For

It is an error to treat the period of deferral and the term of the annuity as simultaneous time periods. For example, if a deferred annuity has a three-year period of deferral and a $10 -$ year annuity term, this is sometimes interpreted, mistakenly, as an annuity ending $10$ years from today. These time segments are separate and consecutive on the timeline! The correct interpretation is that the annuity term ends $13$ years from today, since the $10 -$ year term does not start until the three-year deferral terminates.
A common mistake is to incorrectly determine when the period of deferral ends and the annuity starts. This error usually results from forgetting that the payments on ordinary annuities start one payment interval after the annuity starts, whereas annuity due payments start immediately. Thus, if the first quarterly payment on an ordinary annuity is to be paid $6$ years from today, then the period of deferral is $5$ years and $9$ months. If the deferral is for an annuity due, then the period of deferral is $6$ years.

Example 2.7.1

You borrow $$ 10, 000$ for your business to purchase new computer software. The loan agreement requires you make quarterly payments for $5$ years at $3 %$ compounded quarterly. The first loan payment is due in $2$ years. Calculate the size of the quarterly loan payments.

Solution

Step 1: Draw the timeline for the deferred annuity. Because the payment setting is not specified, the payments occur at the end of the payment interval.

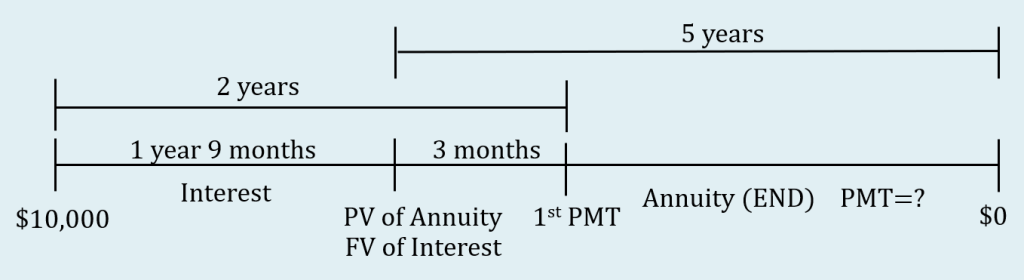
Timeline showing deferred annuity. $10,000 is at the start of the interest period. PV of Annuity and FV of Interest marked at 1 year, 9 months from start of interest period. 3 month interval from PV of Annuity to first payment. 2 years marked from start of interest period to first payment. 5 years marked from PV of annuity to end of timeline. Annuity identified as payments at END with unknown payment. Value at the end of the annuity is $0. — Figure 2.7.2

Some notes about the timeline.

The $$ 10, 000$ is the present value at the start of the interest period.
There is a $2$ year time gap between the start of the interest period and first payment. Because the payments are at the end of the payment interval, the first payment does NOT occur at the same time as the present value of the annuity, which occurs at the beginning of the first payment interval.
Because the payments are at the end of the payment interval, the present value of the annuity occurs one payment interval before the first payment. The payments are quarterly (or $3$ months), so the present value of the annuity occurs $3$ months before the first payment.
The $$ 10, 000$ at the start of the interest period must be moved (with a future value calculation) to the location of the present value of the annuity. Because the present value of the annuity occurs $3$ months before the first payment and it is $2$ years from the start of the interest period to the first payment, the $$ 10, 000$ must move $1$ year and $9$ months ( $2$ years minus $3$ months) to get the location of the present value of the annuity.
The payments for the annuity last for $5$ years.

Step 2: Calculate the future value of the $$ 10, 000$ . As noted above, the $$ 10, 000$ must move to the location of the present value of the annuity, which is $1$ year and $9$ months from the start of the timeline.

$N$

4 \times 1.75 = 7

$P V$

10, 000

$F V$

?

$P M T$

0

$I / Y$

3

$P / Y$

4

$C / Y$

4

$F V = $ 10, 536.961 . . .$

Step 3: Calculate the payment for the annuity. The future value calculated in the previous step becomes the present value for the annuity: $P V = $ 10, 536.961 . . .$

PMT Setting

END

$N$

4 \times 5 = 20

$P V$

10, 536.961 . . .

$F V$

0

$P M T$

?

$I / Y$

3

$P / Y$

4

$C / Y$

4

$P M T = $ 569.32$

Step 4: Write as a statement.

Your quarterly loan payments are $$ 569.32$ .

As you can see with the previous example, sometimes adjustments need to be made to the timing of the period of deferral, depending on the wording of the question and the type of annuity. Because the previous question was an ordinary annuity (payments at the end of the interval) and the timing for the period of deferral was to the first payment, we had to adjust the timing of the interest period so that the money was moved to the location that corresponded to the present value of the annuity.

We are going to do the previous example again, but this time we will treat the annuity as an annuity due (payments at the beginning of the interval). We will do this despite the wording in the question which implies that the annuity has payments at the end of the interval.

Example 2.7.2

You borrow $$ 10, 000$ for your business to purchase new computer software. The loan agreement requires you make quarterly payments for $5$ years at $3 %$ compounded quarterly. The first loan payment is due in $2$ years. Calculate the size of the quarterly loan payments.

Solution

Step 1: Draw the timeline for the deferred annuity. Treat the annuity as an annuity due with the payments at the beginning of the interval.

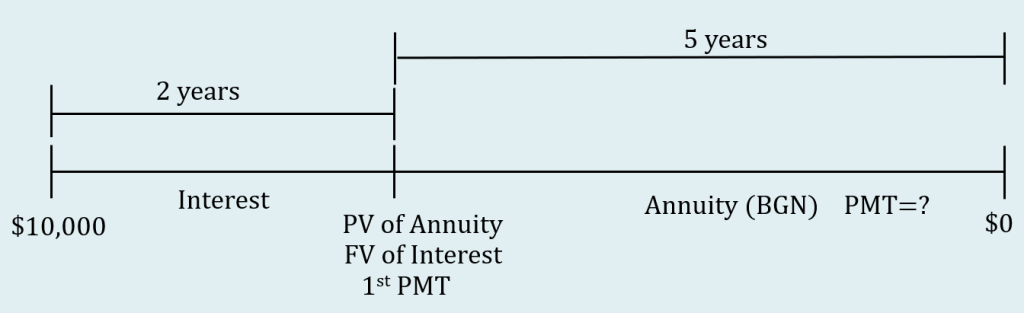
Timeline showing deferred annuity. $10,000 is at the start of the interest period. PV of Annuity, FV of Interest and first payment marked at 2 years from start of interest period. 5 years marked from PV of annuity to end of timeline. Annuity identified as payments at beginning with unknown payment. Value at the end of the annuity is $0. — Figure 2.7.3

Some notes about the timeline.

The $$ 10, 000$ is the present value at the start of the interest period.
Because the payments are at the beginning of the payment interval, the present value of the annuity and the first payment occur at the same time, at the start of the annuity. Note that this eliminates the gap between the present value of the annuity and the first payment seen in the previous example.
The $$ 10, 000$ at the start of the interest period must be moved (with a future value calculation) to the location of the present value of the annuity. Because the present value of the annuity occurs at the time of the first payment, the $$ 10, 000$ must move $2$ years to get the location of the present value of the annuity.
The payments for the annuity last for $5$ years.

Step 2: Calculate the future value of the $$ 10, 000$ . As noted above, the $$ 10, 000$ must move to the location of the present value of the annuity, which is $2$ years from the start of the timeline.

$N$

4 \times 2 = 8

$P V$

10, 000

$F V$

?

$P M T$

0

$I / Y$

3

$P / Y$

4

$C / Y$

4

$F V = $ 10, 615.988 . . .$

Step 3: Calculate the payment for the annuity. The future value calculated in the previous step becomes the present value for the annuity: $P V = $ 10, 615.988 . . .$

PMT Setting

BGN

$N$

4 \times 5 = 20

$P V$

10, 615.988 . . .

$F V$

0

$P M T$

?

$I / Y$

3

$P / Y$

4

$C / Y$

4

$P M T = $ 569.32$

Step 4: Write as a statement.

Your quarterly loan payments are $$ 569.32$ .

Note: Treating the annuity as an annuity due (payments at the beginning of the interval) had no impact on the final answer. But, by treating the annuity as an annuity due, we eliminated the time adjustments required in the first example to get the future value of the interest aligned with the timing of the present value of the annuity. You can always treat a deferred annuity as an annuity due, regardless of the information in the question.

Paths to Success

You can treat any deferred annuity as an ordinary deferred annuity or a deferred annuity due. Regardless of the approach, you will get the same final answer, provided you make the correct adjustments based on your approach. However, it is much easier to treat any deferred annuity as a deferred annuity due (payments at the beginning of the interval). The deferred annuity due approach lines up the future value of the interest, the present value of the annuity and the first payment at the same moment in time, which eliminates any time adjustments to the period of deferral.

Try It

1) You are going to invest $$ 80, 000$ today at $5.5 %$ compounded quarterly. You want to receive month-end payments from this investment for $25$ years. You will receive your first payment in $10$ years. What are the size of your monthly payments?

Solution

PMT Setting		BGN
$N$	$40$	$300$
$P V$	$- 80, 000$	$- 138, 141.661 . . .$
$F V$	$138, 141.661 . . .$	$0$
$P M T$	$0$	$842.40$
$I / Y$	$5.5$	$5.5$
$P / Y$	$4$	$12$
$C / Y$	$4$	$4$

$P M T = $ 842.40$

Example 2.7.3

You want to invest some money today to help fund your retirement. When you retire, you want to receive $$ 5, 000$ at the end of every month for $15$ years. You want to receive your first payment in $20$ years. If your retirement fund earns interest at $5 %$ compounded semi-annually, how much money do you need to invest?

Solution

Step 1: Draw the timeline for the deferred annuity. Using the trick identified above, treat the annuity as an annuity due with the payments at the beginning of the interval (despite the wording in the question that identifies the payments at the end of the interval).

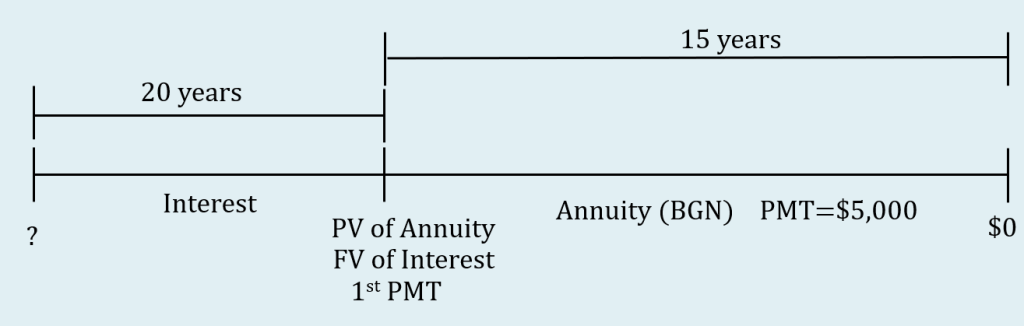
Timeline showing deferred annuity. Unknown present value at the start of the interest period. PV of Annuity, FV of Interest and first payment marked at 20 years from start of interest period. 15 years marked from PV of annuity to end of timeline. Annuity identified as payments at beginning with $5000 payments. Value at the end of the annuity is $0. — Figure 2.7.4

Some notes about the timeline.

The present value at the start of the interest period is unknown.
Because the payments are at the beginning of the payment interval, the present value of the annuity and the first payment occur at the same time, at the start of the annuity. There is a $20$ year gap from the start of the interest period and the present value of annuity/future value of interest/first payment.
The $$ 5, 000$ payments for the annuity last for $15$ years.
The present value of the annuity becomes the future value of the interest period. Then, the future value of the interest period will be moved back $20$ years to the start of the interest period.

Step 2: Calculate the present value of the annuity.

PMT Setting

BGN

$N$

12 \times 15 = 180

$P V$

?

$F V$

0

$P M T$

5, 000

$I / Y$

5

$P / Y$

12

$C / Y$

2

$P V = $ 637, 034.376 . . .$

Step 3: Calculate the present value for the interest period. The present value calculated in the previous step becomes the future value for the interest period: $F V = $ 637, 034.376 . . .$

$N$

2 \times 20 = 40

$P V$

?

$F V$

637, 034.376 . . .

$P M T$

0

$I / Y$

5

$P / Y$

2

$C / Y$

2

$P V = $ 237, 251.11$

Step 4: Write as a statement.

You need to invest $$ 237, 251.11$ today to fund your retirement.

Try It

2) You need to borrow some money for your business. You can afford to pay $$ 1, 250$ every month for $10$ years. You are charged interest at $4.78 %$ compounded semi-annually and will make your first payment in $4$ years. How much money can you borrow?

Solution

PMT Setting	BGN
$N$	$120$	$8$
$P V$	$119, 784.5266 . .$	$99, 160.88$
$F V$	$0$	$- 118, 784.5266 . . .$
$P M T$	$- 1, 250$	$0$
$I / Y$	$4.78$	$4.78$
$P / Y$	$12$	$2$
$C / Y$	$2$	$2$

$P V = $ 99, 160.88$

Example 2.7.4

Bashir has $$ 50, 000$ to invest. Eventually, Bashir wants the annuity to pay him $$ 2, 500$ at the beginning of every month for $10$ years. When can Bashir receive his first payment if the investment earns $8.25 %$ compounded quarterly?

Solution

Step 1: Draw the timeline for the deferred annuity.

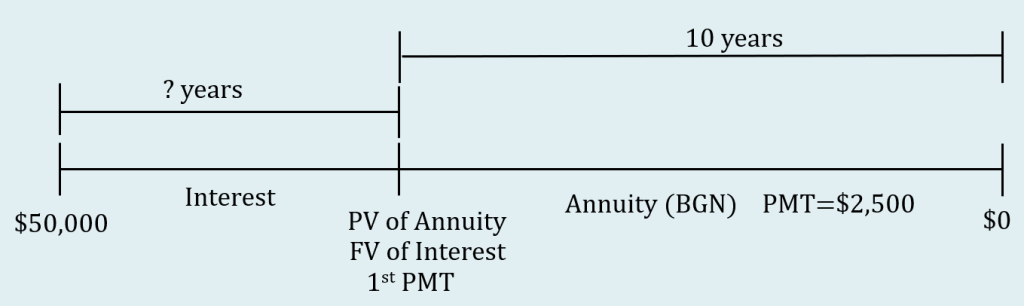
Timeline showing deferred annuity. $50,000 at the start of the interest period. PV of Annuity, FV of Interest and first payment marked at unknown number of years from start of interest period. 10 years marked from PV of annuity to end of timeline. Annuity identified as payments at beginning with $2500 payments. Value at the end of the annuity is $0. — Figure 2.7.5

Some notes about the timeline.

The $$ 50, 000$ is at the start of the interest period.
Because the payments are at the beginning of the payment interval, the present value of the annuity and the first payment occur at the same time, at the start of the annuity.
The time from the start of the interest period to the present value of the annuity/future value of the interest period/first payment is unknown.
The $$ 2, 500$ payments for the annuity last for $10$ years.

Step 2: Calculate the present value of the annuity.

PMT Setting

BGN

$N$

12 \times 10 = 120

$P V$

?

$F V$

0

$P M T$

2, 500

$I / Y$

8.25

$P / Y$

12

$C / Y$

4

$P V = $ 205, 719.154 . . .$

Step 3: Calculate the number of compounding periods for the interest period and convert to years and months. The present value calculated in the previous step becomes the future value for the interest period: $F V = $ 205, 719.154 . . .$

$N$	?
$P V$	$- 50, 000$
$F V$	$205, 719.154 . . .$
$P M T$	$0$
$I / Y$	$8.25$
$P / Y$	$4$
$C / Y$	$4$

$N = 69.286 . . .$

$\begin{array}{rcl} Number of Years & = & \frac{N}{C / Y} \\ = & \frac{69.286 . . .}{4} \\ = & 17.321 . . . \\ \to & 17 years \\ Number of Months & = & 0.321 . . . \times 12 \\ = & 3.858 . . . \\ \to & 4 months \end{array}$

Step 4: Write as a statement.

Bashir can receive his first payment $17$ years and $4$ months after he invests the $$ 50, 000$ .

Try It

3) You want to receive $$ 5, 000$ semi-annual payments for $5.5$ years from a fund earning $6.82 %$ compounded monthly. If you invest $$ 20, 000$ in the fund today, when can you receive your first payment. Give your answer in years and months.

Solution

PMT Setting	BGN
$N$	$11$	$149.5185 . . .$
$P V$	$- 46, 669.472 . . .$	$- 20, 000$
$F V$	$0$	$46, 669.472 . . .$
$P M T$	$5, 000$	$0$
$I / Y$	$6.82$	$6.82$
$P / Y$	$2$	$12$
$C / Y$	$12$	$12$

$N = 149.5185 . . . .$

$\begin{array}{rcl} Number of Years & = & \frac{N}{C / Y} \\ = & \frac{149.518 . . .}{12} \\ = & 12.4598 . . . \\ \to & 12 years \\ Number of Months & = & 0.598 . . . \times 12 \\ = & 5.5185 . . . \\ \to & 6 months \end{array}$

Example 2.7.5

Emile received a $$ 25, 000$ one-time bonus from his employer today, and he immediately invested it at $3.25 %$ compounded semi-annually. Fourteen years from now, he plans to withdraw $$ 2, 300$ every quarter to use as his retirement income. How long can Emile receive these payments?

Solution

Step 1: Draw the timeline for the deferred annuity. Treat the annuity as an annuity due with the payments at the beginning of the interval (despite the wording in the question that identifies the payments at the end of the interval).

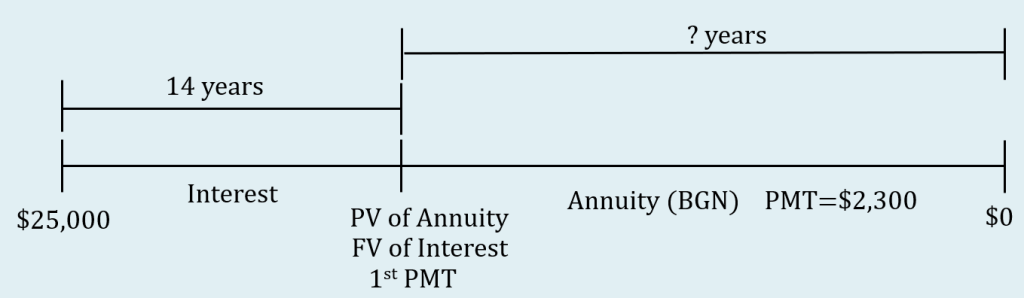
Timeline showing deferred annuity. $25,000 at the start of the interest period. PV of Annuity, FV of Interest and first payment marked at 14 of years from start of interest period. Unknown number of years marked from PV of annuity to end of timeline. Annuity identified as payments at beginning with $2300 payments. Value at the end of the annuity is $0. — Figure 2.7.6

Some notes about the timeline.

The $$ 25, 000$ is at the start of the interest period.
Because the payments are at the beginning of the payment interval, the present value of the annuity and the first payment occur at the same time, at the start of the annuity. There is a $14$ year gap from the start of the interest period and the present value of annuity/future value of interest/first payment.
The $$ 2, 300$ payments for the annuity last for an unknown number of years.

Step 2: Calculate the future value of the $$ 25, 000$ .

$N$

2 \times 14 = 28

$P V$

- 25, 000

$F V$

?

$P M T$

0

$I / Y$

3.25

$P / Y$

2

$C / Y$

2

$F V = $ 39, 260.484 . . .$

Step 3: Calculate the number of payment periods for the annuity and convert to years and months. The future value calculated in the previous step becomes the present value for the annuity: $P V = $ 39, 260.484 . . .$

PMT Setting

BGN

$N$

?

$P V$

- 39, 260.484 . . .

FV

0

PMT

2, 300

I/Y

3.25

P/Y

4

C/Y

2

$N = 18.284 . . . \to 19 payments$

$\begin{array}{rcl} Number of Years & = & \frac{rounded up N}{P / Y} \\ = & \frac{19}{4} \\ = & 4.75 \\ \to & 4 years \\ Number of Months & = & 0.75 \times 12 \\ = & 9 \end{array}$

Step 4: Write as a statement.

Emile can receive payments for $4$ years and $9$ months.

Try It

4) You borrowed $$ 15, 000$ today at $4.5 %$ compounded monthly. The loan agreement requires semi-annual payments of $$ 750$ with the first payment due in $3$ years. How long will you need to make payments to repay the loan?

Solution

PMT Setting		BGN
$N$	$36$	$31.602 . . .$
$P V$	$15, 000$	$17, 163.717 . . .$
$F V$	$- 17, 163.717 . . .$	$0$
$P M T$	$0$	$- 750$
$I / Y$	$4.5$	$4.5$
$P / Y$	$12$	$2$
$C / Y$	$12$	$12$

$N = 31.602 . . . \to 32 payments$

$\begin{array}{rcl} Number of Years & = & \frac{rounded up N}{P / Y} \\ = & \frac{32}{2} \\ = & 16 years \end{array}$

Section 2.7 Exercises

How much money should a company borrow at $7.7 %$ compounded semi-annually in order to repay $$ 4, 200$ at the end of every quarter for $12$ years. The first payment is due $15.5$ years from now.

Solution

$$ 41, 484$
You purchase an annuity for $$ 40, 000$ . The annuity will pay you beginning-of-the-month payments for $10$ years and you will receive your first payment in $5$ years. If the annuity earns $6.1 %$ compounded quarterly, what is the size of the payments?

Solution

$$ 599.92$
Your company took out a $$ 100, 000$ business loan at $8.5 %$ effective. The loan agreement calls for payments of $$ 20, 000$ at the beginning of every six months with the first payment made in $7$ years. How long will the company need to make payments to repay the loan?

Solution

$5$ years, $6$ months
You invest $$ 17, 500$ in an account at $7.5 %$ compounded monthly. You want to withdraw annual payments from the account for $5$ years. If you receive the first payment in $14.5$ years, what is the size of the payments you will receive?

Solution

$$ 11, 951.16$
You want to receive quarterly payments of $$ 750$ from your investment fund for a period of $13$ years. The fund earns $2.8 %$ compounded compounded semi-annually. Calculate the amount of money you need to deposit in the fund if the first payment is to be received in $7$ years and $9$ months.

Solution

$$ 26, 476.06$
You invest $$ 55, 000$ in a fund earning $6.6 %$ compounded quarterly. You want to withdraw $$ 900$ from the fund at the end of every month with the first withdrawal to be made $4$ years from now. How long will it take for the fund to be depleted?

Solution

$8$ years, $8$ months
What is the present value of a deferred annuity with a deferral period of $17$ years at $6.7 %$ compounded semi-annually followed by a $10 -$ year annuity due paying $$ 1, 250$ every month at $4.78 %$ compounded semi-annually?

Solution

$$ 39, 070.09$
If $$ 38, 000$ is invested for $15$ years at $9.4 %$ compounded quarterly and then pays out $$ 10, 000$ at the beginning of each year while earning $2.4 %$ compounded annually, how far from today would the last payment occur?

Solution

$19$ years
Jeff and Sarah want to invest some money in an RESP earning $4 %$ compounded quarterly for their daughter’s education. They want the annuity to pay their daughter $$ 1, 000$ monthly for three years and nine months for the duration of her educational studies. What lump-sum amount do they need to invest today if they want their daughter to receive the first payment in $10$ years?

Solution

$$ 28, 123.56$
Parker invested $$ 80, 000$ in a fund earning $3.85 %$ effective. He wants to receive month-end payments from the fund for $25$ years. Calculate the size of Parker’s payments if he receives his first payment in $10$ years.

Solution

$$ 600.36$
Amber plans to retire in $40$ years. When she does retire, she would like her RRSP to pay her $$ 2, 500$ every month for $20$ years. How much money does Amber need to invest today if the RRSP earns $5.9 %$ compounded semi-annually?

Solution

$$ 34, 735.26$

Attribution

“12.1: Deferred Annuities” from Business Math: A Step-by-Step Handbook Abridged by Sanja Krajisnik; Carol Leppinen; and Jelena Loncar-Vines is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

“12.1: Deferred Annuities” from Business Math: A Step-by-Step Handbook (2021B) by J. Olivier and Lyryx Learning Inc. through a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License unless otherwise noted.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

2.7 Deferred Annuities

Learning Objectives

Formula & Symbol Hub

Symbols Used

Formulas Used

Formula 2.1 – Total Number of Payments (Annuity)

Formula 2.2 – Future Value of Ordinary Annuity

Formula 2.3 – Future Value of Annuity Due

Formula 2.4 – Present Value of Ordinary Annuity

Formula 2.5 – Present Value of Annuity Due

Introduction

What is a Deferred Annuity?

Working with Deferred Annuities

Things to Watch Out For

Example 2.7.1

Example 2.7.2

Paths to Success

Try It

Example 2.7.3

Try It

Example 2.7.4

Try It

Example 2.7.5

Try It

Section 2.7 Exercises

Attribution

License

Share This Book