4.1 Bond Terminology
Learning Objectives
- Understand terminology used in bonds and bond transactions
Formula & Symbol Hub
Symbols Used
- [latex]BAL[/latex] = Principal balance
- [latex]BV[/latex] = Book value
- [latex]FV[/latex] = Face value of bond
- [latex]PMT[/latex] = Annuity payment amount
- [latex]N[/latex] = Number of annuity payments
- [latex]I/Y[/latex] = Nominal interest rate
- [latex]P/Y[/latex] = Number of payments per year or payment frequency
- [latex]C/Y[/latex] = Number of compounds per year or compounding frequency
Formulas Used
-
Formula 4.1 – Bond Payment
[latex]\text{Payment}=\mbox{Face Value} \times \mbox{periodic bond rate}[/latex]
Introduction
A marketable bond is a debt that is secured by a specific corporate asset, that establishes the issuer’s responsibility toward a creditor for paying interest at regular intervals, and for repaying the principal at a fixed later date. A debenture is the same as a marketable bond, except that the debt is not secured by any specific corporate asset. Mathematically, the calculations are identical for these two financial tools, which this textbook refers to as bonds for simplicity.
Bond Terminology
- Issue Date. The bond issue date is the date that the bond is issued and available for purchase by creditors. Interest accrues from this date.
- Face Value. Also called the par value or denomination of the bond, the face value is the principal amount of the debt. It is what the investor lent to the bond-issuing corporation. The amount, usually a multiple of [latex]\$100[/latex], is found in small denominations up to [latex]\$10,000[/latex] for individual investors and larger denominations up to [latex]\$50,000[/latex] or more for corporate investors.
- Coupon Rate. Also known as the bond rate or nominal rate, the coupon rate is the nominal interest rate paid on the face value of the bond. The coupon rate is fixed for the life of the bond. Most commonly the interest is calculated semi-annually and payable at the end of every six-month period over the entire life of the bond, starting from the issue date. All coupon rates used in this textbook are assumed to be semi-annually compounded, unless stated otherwise.
- Yield Rate. The yield rate, or market rate, is the prevailing nominal rate of interest in the open bond market. Because bonds are actively traded, this rate fluctuates based on economic and financial conditions. On the issue date, the market rate determines the coupon rate that is tied to the bond. Market rates are usually compounded semi-annually, as will be assumed in this textbook unless otherwise stated. Therefore, marketable bonds form ordinary simple annuities, because the interest payments and the market rate are both compounded semi-annually, and the payments occur at the end of the interval.
- Redemption Value. Also called the redemption price or maturity value, the redemption value is the amount the bond issuer will pay to the bondholder upon maturity of the bond. The redemption price normally equals the face value of the bond, in which case the bond is said to be “redeemable at par” because interest on the bond has already been paid in full periodically throughout the term, leaving only the principal in the account. In some instances a bond issuer may in fact redeem the bond at a premium, which is a price greater than the face value. The redemption price is then stated as a percentage of the face value, such as [latex]103\%[/latex]. For introductory purposes, this textbook sticks to the most common situation, where the redemption price equals the face value.
- Maturity Date. Also known as the redemption date or due date, the maturity date is the day upon which the redemption price will be paid to the bondholder (along with the final interest payment), thereby extinguishing the debt.
- Selling Date. The date that a bond is actively traded and sold to another investor through the bond market is known as the selling date. In the timeline, the selling date can appear anywhere on the timeline between the issue date and maturity date, and it may occur more than once as the bond is sold by one investor after another.
- Purchase Price. The purchase price is the price the bond holder pays to purchase the bond. Although the redemption value and the periodic interest payments remain fixed throughout the lifetime of the bond, the purchase price fluctuates depending on various market conditions, such as the current yield rate.
Example 4.1.1
A [latex]\$10,000[/latex] bond was issued on March 1, 2019 with a [latex]7\%[/latex] coupon and [latex]16[/latex] years to maturity. The bond was purchased on July 13, 2023 when the yield to maturity was [latex]5\%[/latex].
- Face Value (or Redemption Value) = [latex]\$10,000[/latex]
- Issue Date = March 1, 2019
- Purchase Date (or Selling Date) = July 23, 2023
- Maturity Date (or Redemption Date) = March 1, 2035
- Coupon Rate = [latex]7\%[/latex] compounded semi-annually
- Yield Rate = [latex]5\%[/latex] compounded semi-annually
Things to Watch Out For
Unless otherwise stated, the coupon rate and the yield rate are compounded semi-annually and the coupon payments are made every six months.
In this chapter we only deal with bonds that are redeemed for their face value at the time of maturity. So, the redemption value of the bond will equal its face value.
Premium, Discount, and At Par Bonds
The price at which a bond is purchased in the market may not be the face value of the bond. In fact, the price of a bond fluctuates with the market rate over time. There are three scenarios relating the purchase price of the bond to its face value.
- Bonds purchased at par. The purchase price of the bond equals its face value. This happens when the coupon rate equals the yield rate.
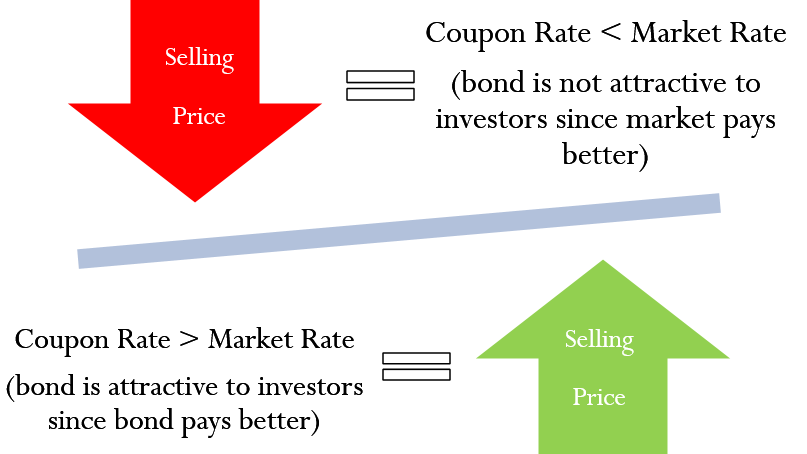
- Bonds purchased at premium. The purchase price of the bond is higher than its face value. This happens when the coupon rate is greater than the yield rate. In such cases, the bond is providing a higher rate of return (through the coupons) than an investment in the market (earning the lower yield rate). Consequently, the bond will be in demand and will sell at a higher price that its face value. The difference between the purchase price and the face value is called the premium.
- Bonds purchased at discount. The purchase price of the bond is lower than its face value. This happens when the coupon rate is less than the yield rate. In such cases, the bond is providing a lower rate of return (through the coupons) than an investment in the market (earning the higher yield rate). Consequently, the bond will not be in demand and will sell at a lower price that its face value. The difference between the face value and the purchase price is called the discount.
Example 4.1.2
Identify each of the following bonds as premium, discount, or at par.
- A [latex]\$5,000[/latex] bond with a [latex]3\%[/latex] coupon is purchased when there are five years to maturity and the yield to maturity is [latex]4.5\%[/latex].
- A [latex]\$12,000[/latex] bond with a [latex]4\%[/latex] coupon is purchased when there are ten years to maturity and the yield to maturity is [latex]4\%[/latex].
- A [latex]\$7,000[/latex] bond with a [latex]6\%[/latex] coupon is purchased when there are twelve years to maturity and the yield to maturity is [latex]3.7\%[/latex].
Solution
- Discount because the coupon rate ([latex]3\%[/latex]) is less than the yield rate ([latex]4.5\%[/latex])
- At par because the coupon rate and yield rate are equal.
- Premium because the coupon rate ([latex]6\%[/latex]) is higher than the yield rate ([latex]3.7\%[/latex]).
Calculating the Bond Payment
The bond payment, or coupon payment, is the payment the bond holder received semi-annually throughout the investment. This interest is not converted to the principal of the bond, and therefore does not compound. Instead, the bond payment is directly paid to the bond holder. The amount of the bond payment depends only on the face value of the bond and the coupon rate.
[latex]\boxed{4.1}[/latex] Bond Payment
[latex]\Large{\color{red}{Bond\;Payment}}={\color{blue}{FV}}\times{\color{green}{b}}[/latex]
- [latex]{\color{red}{\text{Bond Payment:}}}[/latex] is the payment the bond holder received semi-annually throughout the investment.
- [latex]{\color{blue}{FV}}\;\text{is the Face Value:}[/latex] of the bond when the bond is redeemed at maturity.
- [latex]{\color{green}{b}}\;\text{is Periodic Coupon Rate:}[/latex] where [latex]b=\frac{\mbox{coupon rate}}{\mbox{number of coupons per year}}[/latex]
Example 4.1.3
A [latex]\$5,000[/latex] bond has a [latex]3\%[/latex] coupon. Calculate the bond payment.
Solution
[latex]\begin{eqnarray*} \mbox{Bond Payment} & = & FV \times b \\ & = & 5,000 \times \frac{0.03}{2} \\ & = & $75 \end{eqnarray*}[/latex]
Key Takeaways
Remember, the bond payments and coupon rate are assumed to be semi-annual, unless stated otherwise.
For the bond in the previous example, the bond holder will receive a [latex]\$75[/latex] payment at the end of every six months over the life time of the bond.
Try It
1) A [latex]\$12,000[/latex] bond has a [latex]7\%[/latex] coupon. Calculate the bond payment.
Solution
[latex]\begin{eqnarray*} \mbox{Bond Payment} & = & FV \times b \\ & = & 12,000 \times \frac{0.07}{2} \\ & = & $420 \end{eqnarray*}[/latex]
Attribution
“7.1 Bond Terminology” from Business and Financial Mathematics by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.
“14.1: Determining the Value of a Bond” from Business Math: A Step-by-Step Handbook (2021B) by J. Olivier and Lyryx Learning Inc. through a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License unless otherwise noted.

