4.5 Quotation of Bonds
Learning Objectives
- Calculate the purchase price of a bond on a non-interest payment date
- Calculate the quoted price of a bond
Formula & Symbol Hub
Symbols Used
- [latex]BAL[/latex] = Principal balance
- [latex]BV[/latex] = Book value
- [latex]FV[/latex] = Face value of bond
- [latex]PMT[/latex] = Annuity payment amount
- [latex]N[/latex] = Number of annuity payments
- [latex]I/Y[/latex] = Nominal interest rate
- [latex]P/Y[/latex] = Number of payments per year or payment frequency
- [latex]C/Y[/latex] = Number of compounds per year or compounding frequency
Formulas Used
-
Formula 4.1 – Bond Payment
[latex]\text{Payment}=\mbox{Face Value} \times \mbox{periodic bond rate}[/latex]
-
Formula 4.2 – Purchase Price on an Interest Payment Date
[latex]\text{Purchase Price}=\mbox{Present Value of Face Value}+\mbox{Present Value of Bond Payments}[/latex]
-
Formula 4.3 – Premium (Bonds)
[latex]\text{Premium}=\mbox{Purchase Price}-\mbox{Face Value}[/latex]
-
Formula 4.4 – Discount (Bonds)
[latex]\text{Discount}=\mbox{Face Value}-\mbox{Purchase Price}[/latex]
-
Formula 4.5 – Quoted Price (Bonds)
[latex]\mbox{Flat Price}-\mbox{Accrued Interest}[/latex]
-
Formula 4.6 – Quoted Price as a Percentage of Face Value
[latex]\frac{\mbox{Quoted Price}}{\mbox{Face Value}} \times 100\%[/latex]
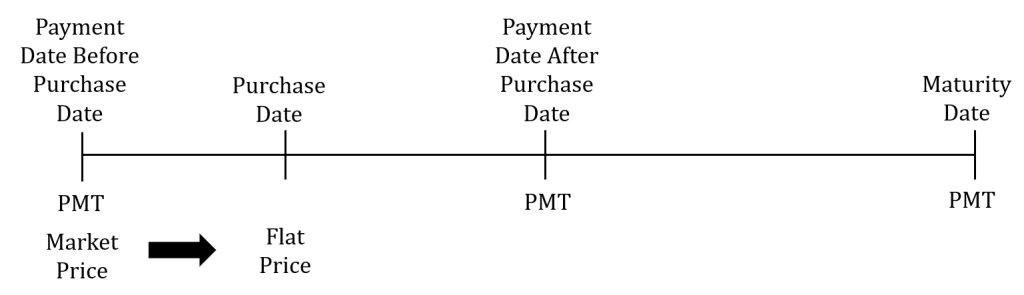
Calculating the Purchase Price of a Bond on a Non-Interest Payment Date
In a previous section, we learned how to calculate the purchase price of a bond when the bond is purchased on an interest payment date. But, bonds can be bought or sold on any day of the year. How do we calculate the purchase price when a bond is purchased on a non-interest payment date?
For each day that elapses after an interest payment date, interest for the next payment starts to accrue. When the bond is sold in between interest payment dates, the interest, called the accrued interest, that accrues on the bond since the interest payment date before the purchase date up to but not including the purchase date is paid to the seller. This accrued interest is included in the purchase price paid to the seller. That is, the buyer has to pay the seller the purchase price of the bond on the previous interest payment date, called the market price, plus the accrued interest. The market price plus the accrued interest is called the flat price, and is the actual amount the buyer pays the seller on the purchase date.
Why does the buyer have to pay the seller the accrued interest? Suppose a bond makes semi-annual interest payments of [latex]\$50[/latex] and the buyer acquires the bond two months after the last interest payment date. Because the seller held the bond for two months of the six-month payment interval, it is fair and reasonable for the seller to receive the interest earned during those two months. However, the next interest payment occurs four months after the sale of the bond, at which time the buyer, who now owns the bond, will receive the full [latex]\$50[/latex] interest payment for the full six month payment interval. Thus, at the time of buying the bond, the buyer has to pay the seller the bond’s market price plus the portion of the next interest payment that legally belongs to the seller. In this example, an interest amount representing two of the six months needs to be paid.
Arriving at the bond’s purchase price in between interest payment dates is a little complex because the flat price is increasing according to a compound interest formula, but in practice the accrued interest on the bond is increasing according to a simple interest formula. If this seems peculiar to you, you would be right, but that is just how bonds happen to work!
HOW TO
Find the Flat Price of a Bond
Follow these steps to find the flat price, the actual purchase price of a bond between interest payment dates.
Step 1: Identify four important dates:
-
- Purchase date.
- Maturity date.
- Interest payment date immediately before the purchase date.
- Interest payment date immediately after the purchase date.
Step 2: Calculate the market price on the interest payment date immediately before the purchase date. The market price is the purchase price if the bond is actually purchased on the interest payment date immediately before the purchase date. This calculation is the same purchase price calculation we learned in a previous section.
Step 3: Calculate the flat price on the purchase date by adding the accrued interest to the market price. This is a compound interest only calculation that moves the market price from the payment date immediately before the purchase date to the purchase date. In this calculation, you calculate the future value with the present value set to the market price from the previous step, the payment is [latex]0[/latex], the interest rate is the yield rate, and [latex]N[/latex] is
[latex]\begin{eqnarray*} & & \\ N & = & \frac{\mbox{Number of days from previous interest payment date to purchase date}}{\mbox{Number of days in between interest payment dates}} \end{eqnarray*}[/latex]
Key Takeaways
The market price is the purchase price on the payment date before the purchase price. That is, if the actual purchase date was this payment date, you would pay the market price to buy the bond.
Two things happen on the maturity date: the investor receives the face value of the bond and the last bond payment. Consequently, the maturity date is a payment date. Because the payments happen on the same two dates of every year, the month and day of the maturity date tells you one of the payment dates. The other payment date happens six months later (or six months earlier depending on how you think about it) on the same day. For example, suppose the maturity date is January 1, 2040. This means that January 1 is one of the two payment dates. The other payment date happens six months later, in this case July 1.
Example 4.5.1
A [latex]\$1,000[/latex] bond with a [latex]7\%[/latex] coupon has a maturity date of February 1, 2035. The bond was purchased on May 20, 2023 when the yield to maturity was [latex]5\%[/latex]. Calculate the purchase price.
Solution
Step 1: Identify the four dates.
Because February 1 is the maturity date, February 1 is one of the two payment dates. The other payment date is six months later, in this case August 1.
-
- Purchase date: May 20, 2023
- Maturity date: February 1, 2035
- Payment date before purchase date: February 1, 2023
- Payment date after purchase date: August 1, 2023

Step 2: Calculate the market price on February 1, 2023.
The time for this calculation is the number of years between February 1, 2023 (the payment date before the purchase date) and February 1, 2035 (the maturity date), which is [latex]12[/latex] years.
Because no other information is given, the frequency of the payments and the compounding frequencies (for the coupon rate and the yield rate) are assumed to be semi-annual. The given information is
[latex]\begin{eqnarray*} FV & = & \$1,000 \\ P/Y & = & 2 \\ I/Y & = & 5\% \\ C/Y & = & 2 \\ t & = & 12 \mbox{ years} \\ \mbox{Coupon Rate} & = & 7\% \\\\ PMT & = & FV \times \frac{\mbox{coupon rate}}{2} \\ & = & 1,000\times \frac{0.07}{2}\\ & = & \$35 \end{eqnarray*}[/latex]
| PMT Setting | END |
| [latex]N[/latex] | [latex]2 \times 12=24[/latex] |
| [latex]PV[/latex] | [latex]?[/latex] |
| [latex]FV[/latex] | [latex]1,000[/latex] |
| [latex]PMT[/latex] | [latex]35[/latex] |
| [latex]I/Y[/latex] | [latex]5[/latex] |
| [latex]P/Y[/latex] | [latex]2[/latex] |
| [latex]C/Y[/latex] | [latex]2[/latex] |
[latex]PV=\$1,178.85[/latex]
The market price on February 1, 2023 is [latex]\$1,178.85[/latex].
Step 3: Calculate the flat price on May 20, 2023.
This is a compound interest calculation that moves the market price from the previous step forward in time to the purchase date. The value of [latex]N[/latex] for this compound interest calculation is
[latex]\begin{eqnarray*}N & = & \frac{\mbox{Number of days from February 1, 2023 to May 20, 2023}}{\mbox{Number of days from February 1, 2023 to August 1, 2023}} \\ & = & \frac{108}{181}\end{eqnarray*}[/latex]
| N | [latex]\frac{108}{181}[/latex] |
| PV | [latex]1,178.85[/latex] |
| FV | [latex]?[/latex] |
| PMT | [latex]0[/latex] |
| I/Y | [latex]5[/latex] |
| P/Y | [latex]2[/latex] |
| C/Y | [latex]2[/latex] |
[latex]FV=\$1,196.35[/latex]
Step 4: Write as a statement.
The flat price on May 20, 2023 is [latex]\$1,196.35[/latex]. This is the purchase price of the bond on May 20, 2023.
 Paths to Success
Paths to Success
In the above example, the market price of [latex]\$1,178.85[/latex] is the purchase price if you purchased the bond on February 1, 2023.
To calculate the number of days between the dates in Step 3, use the DATE function on the financial calculator.
In step [latex]3[/latex] above, you will need to convert the fraction [latex]\frac{108}{181}[/latex] to a decimal in order to enter it into your calculator. Remember to keep all of the decimals when you enter this number into N to avoid any possible round-off error.
The flat price calculation in step [latex]3[/latex] is a compound interest only calculation, which means the payment is [latex]0[/latex]. This is a future value calculation because the market price is moving forward in time to get to the purchase date. The interest rate for this calculation is the yield rate.
Using the TI BAII Plus Calculator to Count the Number of Days Between Dates
To count the number of days between two dates:
-
- Press 2nd DATE (the [latex]1[/latex] button) to enter the date worksheet.
- At the [latex]DT1[/latex] screen, enter the first date. Dates are entered in the form mm.ddyy. For example, enter May 19, 2023 as [latex]05.1923[/latex]. After entering the date press ENTER.
- Press the down arrow.
- At the [latex]DT2[/latex] screen, enter the second date. Dates are entered in the form mm.ddyy. For example, enter August 7, 2023 as [latex]08.0723[/latex]. After entering the date press ENTER.
- Press the down arrow.
- At the [latex]DBD[/latex] screen press [latex]CPT[/latex] to calculate the number of days between the two entered dates. For example, there are [latex]80[/latex] days between May 19, 2023 and August 7, 2023.
Video: Calculating Dates and Days (Month-Day-Year) by Joshua Emmanuel [3:32] Transcript Available.
Example 4.5.2
A 25-year, [latex]\$2,000[/latex] bond with a [latex]3\%[/latex] coupon was issued on April 1, 2018. The bond was purchased on January 27, 2023 when the yield to maturity was [latex]8\%[/latex]. Calculate the purchase price.
Solution
Step 1: Identify the four dates.
The bond was issued on April 1, 2018 and reaches maturity [latex]25[/latex] years later. So, the maturity date is April 1, 2043. Because April 1 is the maturity date, April 1 is one of the two payment dates. The other payment date is six months later, in this case October 1.
-
- Purchase date: January 27, 2023
- Maturity date: April 1, 2043
- Payment date before purchase date: October 1, 2022
- Payment date after purchase date: April 1, 2023

Step 2: Calculate the market price on October 1, 2022.
The time for this calculation is the number of years between October 1, 2022 (the payment date before the purchase date) and April 1, 2043 (the maturity date), which is [latex]20.5[/latex] years.
Because no other information is given, the frequency of the payments and the compounding frequencies (for the coupon rate and the yield rate) are assumed to be semi-annual. The given information is
[latex]\begin{eqnarray*} FV & = & \$2,000 \\ P/Y & = & 2 \\ I/Y & = & 8\% \\ C/Y & = & 2 \\ t & = & 20.5 \mbox{ years} \\ \mbox{Coupon Rate} & = & 3\% \\\\ PMT & = & FV \times \frac{\mbox{coupon rate}}{2} \\ & = & 2,000\times \frac{0.03}{2}\\ & = & \$30 \end{eqnarray*}[/latex]
| PMT Setting | END |
| [latex]N[/latex] | [latex]2 \times 20.5=41[/latex] |
| [latex]PV[/latex] | [latex]?[/latex] |
| [latex]FV[/latex] | [latex]2,000[/latex] |
| [latex]PMT[/latex] | [latex]30[/latex] |
| [latex]I/Y[/latex] | [latex]8[/latex] |
| [latex]P/Y[/latex] | [latex]2[/latex] |
| [latex]C/Y[/latex] | [latex]2[/latex] |
[latex]PV=\$1,000.35[/latex]
The market price on October 1, 2022 is [latex]\$1,000.35[/latex].
Step 3: Calculate the flat price on January 27, 2023.
This is a compound interest calculation that moves the market price from the previous step forward in time to the purchase date. The value of N for this compound interest calculation is
[latex]\begin{eqnarray*}N & = & \frac{\mbox{Number of days from October 1, 2022 to January 27, 2023}}{\mbox{Number of days from October 1, 2022 to April 1, 2023}} \\ & = & \frac{118}{182}\end{eqnarray*}[/latex]
| N | [latex]\frac{118}{182}[/latex] |
| [latex]PV[/latex] | [latex]1,000.35[/latex] |
| [latex]FV[/latex] | [latex]?[/latex] |
| [latex]PMT[/latex] | [latex]0[/latex] |
| [latex]I/Y[/latex] | [latex]8[/latex] |
| [latex]P/Y[/latex] | [latex]2[/latex] |
| [latex]C/Y[/latex] | [latex]2[/latex] |
[latex]FV=\$1,026.11[/latex]
Step 4: Write as a statement.
The flat price on January 27, 2023 is [latex]\$1,026.11[/latex]. This is the purchase price of the bond on January 27, 2023.
Try It
1) A [latex]\$5,000[/latex] bond with a [latex]4.7\%[/latex] coupon has a maturity date of December 1, 2040. The bond was purchased on September 19, 2023 when the yield rate as [latex]5.9\%[/latex]. Calculate the purchase price.
Solution
The four dates are
- Purchase date: September 19, 2023
- Maturity date: December 1, 2040
- Payment date before purchase date: June 1, 2023
- Payment date after purchase date: December [latex]1, 2023[/latex]
Calculate the market price on June 1, 2023.
[latex]\begin{eqnarray*} PMT & = & FV \times \frac{\mbox{coupon rate}}{2} \\ & = & 5,000\times \frac{0.047}{2}\\ & = & \$117.50\end{eqnarray*}[/latex]
| PMT Setting | END |
| [latex]N[/latex] | [latex]2 \times 17.5=25[/latex] |
| [latex]PV[/latex] | [latex]?[/latex] |
| [latex]FV[/latex] | [latex]5,000[/latex] |
| [latex]PMT[/latex] | [latex]117.50[/latex] |
| [latex]I/Y[/latex] | [latex]5.9[/latex] |
| [latex]P/Y[/latex] | [latex]2[/latex] |
| [latex]C/Y[/latex] | [latex]2[/latex] |
[latex]PV=\$4,350.65[/latex]
Calculate the flat price on September 19, 2023.
| [latex]N[/latex] | [latex]\frac{110}{183}[/latex] |
| [latex]PV[/latex] | [latex]4,350.65[/latex] |
| [latex]FV[/latex] | [latex]?[/latex] |
| [latex]PMT[/latex] | [latex]0[/latex] |
| [latex]I/Y[/latex] | [latex]5.9[/latex] |
| [latex]P/Y[/latex] | [latex]2[/latex] |
| [latex]C/Y[/latex] | [latex]2[/latex] |
[latex]FV=\$4,427.35[/latex]
Quotation of Bonds
The flat price we calculated in the previous examples is the actual price a buyer would pay to purchase those bonds on the given purchase date. The flat price is the market price (on the payment date before the purchase date) plus any interest that has accrued since the previous payment. However, two different bonds purchased on the same day can have very different amounts of accrued interest, depending on where the purchase date is in relation to each bond’s payment date. This can make it very difficult for an investor to directly compare the price of the bonds.
To make a meaningful comparison of bond prices, the flat prices are adjusted for their differing amount of accrued interest. The quoted price of bond is the flat price excluding the accrued coupon interest.
[latex]\boxed{4.5}[/latex] Quoted Price (Bonds)
[latex]\begin{eqnarray*}{\color{red}{\mbox{Quoted Price}}} & = & {\color{blue}{\mbox{Flat Price}}}-{\color{green}{\mbox{Accrued Interest}}}\\ \\ {\color{green}{\mbox{Accrued Interest}}} & = & {\color{purple}{PMT}}\times\frac{{\color{Peach}{\mbox{# days from previous interest pmt date to purchase date}}}}{{\color{RubineRed}{\mbox{# days in between interest pmt dates}}}} \end{eqnarray*}[/latex]
NOTE
The fraction used to find the accrued interest is the same fraction calculated in Step 3 of the the flat price calculations above.
Quoted prices for bonds are normally given as a percent of their face value. This is the market quotation of the bond. Market quotations allow investors to easily compare bond prices.
[latex]\boxed{4.6}[/latex] Market Quotation as a Percentage of Face Value
[latex]\Large\begin{eqnarray*}{\color{red}{\mbox{Percent of Face Value}}} & = & \frac{{\color{blue}{\mbox{Quoted Price}}}}{{\color{green}{\mbox{Face Value}}}} {\color{purple}{\times100\%}} \end{eqnarray*}[/latex]
Example 4.5.3
A [latex]\$1,000[/latex] bond with a [latex]7\%[/latex] coupon has a maturity date of February 1, 2035. The bond was purchased on May 20, 2023 when the yield to maturity was [latex]5\%[/latex]. Calculate the quoted price as a percentage of face value.
Solution
The flat price of the bond on May 20, 2023 is [latex]\$1,196.35[/latex] (found in the first example above).
Step 1: Calculate the accrued interest.
[latex]\begin{eqnarray*}\mbox{Accrued Interest} & = & PMT \times \frac{\mbox{Number of days from February 1, 2023 to May 20, 2023}}{\mbox{Number of days from February 1, 2023 to August 1, 2023}} \\ & = & 35 \times \frac{108}{181} \\ & = & \$20.88 \end{eqnarray*}[/latex]
Step 2: Calculate the quoted price.
[latex]\begin{eqnarray*} \mbox{Quoted Price} & = & \mbox{Flat Price}- \mbox{Accrued Interest} \\ & = & 1,196.35-20.88 \\ & = & \$1,175.47\end{eqnarray*}[/latex]
Step 3: Calculate the quoted price as a percentage of face value.
[latex]\begin{eqnarray*} \mbox{Percent of Face Value} & = & \frac{\mbox{Quoted Price}}{\mbox{Face Value}} \times 100\% \\ & = & \frac{1,175.47}{1,000} \times 100\% \\ & = & 117.55\%\end{eqnarray*}[/latex]
Step 4: Write as a statement.
The quoted price as a percentage of face value is [latex]117.55\%[/latex].
Example 4.5.4
A [latex]\$8,000[/latex] bond with a [latex]4\%[/latex] coupon has a maturity date of November 1, 2037. The bond was purchased on February 5, 2023 when the yield to maturity was [latex]7.5\%[/latex]. Calculate the quoted price as a percentage of face value.
Solution
Step 1: Identify the four dates.
Because November 1 is the maturity date, November 1 is one of the two payment dates. The other payment date is six months later, in this case May 1.
-
- Purchase date: February 5, 2023
- Maturity date: November [latex]1, 2037[/latex]
- Payment date before purchase date: November 1, 2022
- Payment date after purchase date: May 1, 2023

Step 2: Calculate the market price on November 1, 2022.
The time for this calculation is the number of years between November [latex]1, 2022[/latex] (the payment date before the purchase date) and November [latex]1, 2037[/latex] (the maturity date), which is [latex]15[/latex] years.
Because no other information is given, the frequency of the payments and the compounding frequencies (for the coupon rate and the yield rate) are assumed to be semi-annual. The given information is
[latex]\begin{eqnarray*} FV & = & \$8,000 \\ P/Y & = & 2 \\ I/Y & = & 7.5\% \\ C/Y & = & 2 \\ t & = & 15 \mbox{ years} \\ \mbox{Coupon Rate} & = & 4\% \end{eqnarray*}[/latex]
[latex]\begin{eqnarray*} PMT & = & FV \times \frac{\mbox{coupon rate}}{2} \\ & = & 8,000\times \frac{0.04}{2}\\ & = & \$160\end{eqnarray*}[/latex]
| PMT Setting | END |
| [latex]N[/latex] | [latex]2 \times 15=30[/latex] |
| [latex]PV[/latex] | [latex]?[/latex] |
| [latex]FV[/latex] | [latex]8,000[/latex] |
| [latex]PMT[/latex] | [latex]160[/latex] |
| [latex]I/Y[/latex] | [latex]7.5[/latex] |
| [latex]P/Y[/latex] | [latex]2[/latex] |
| [latex]C/Y[/latex] | [latex]2[/latex] |
[latex]PV=\$5,503.91[/latex]
The market price on November 1, 2022 is [latex]\$5,503.91[/latex].
Step 3: Calculate the flat price on February 5, 2023.
This is a compound interest calculation that moves the market price from the previous step forward in time to the purchase date. The value of N for this compound interest calculation is
[latex]\begin{eqnarray*}N & = & \frac{\mbox{Number of days from November 1, 2022 to February 5, 2023}}{\mbox{Number of days from November 1, 2022 to May 1, 2023}} \\ & = & \frac{96}{181}\end{eqnarray*}[/latex]
| [latex]N[/latex] | [latex]\frac{96}{181}[/latex] |
| [latex]PV[/latex] | [latex]5,503.91[/latex] |
| [latex]FV[/latex] | [latex]?[/latex] |
| [latex]PMT[/latex] | [latex]0[/latex] |
| [latex]I/Y[/latex] | [latex]7.5[/latex] |
| [latex]P/Y[/latex] | [latex]2[/latex] |
| [latex]C/Y[/latex] | [latex]2[/latex] |
[latex]FV=\$5,612.43[/latex]
The flat price on February 5, 2023 is [latex]\$5,612.43[/latex].
Step 4: Calculate the accrued interest.
[latex]\begin{eqnarray*}\mbox{Accrued Interest} & = & PMT \times \frac{\mbox{Number of days from November 1, 2022 to February 5, 2023}}{\mbox{Number of days from November 1, 2022 to May 1, 2023}} \\ & = & 160 \times \frac{96}{181} \\ & = & \$84.86 \end{eqnarray*}[/latex]
Step 5: Calculate the quoted price.
[latex]\begin{eqnarray*} \mbox{Quoted Price} & = & \mbox{Flat Price}- \mbox{Accrued Interest} \\ & = & 5,612.43-84.86 \\ & = & \$5,527.57\end{eqnarray*}[/latex]
Step 6: Calculate the quoted price as a percentage of face value.
[latex]\begin{eqnarray*} \mbox{Percent of Face Value} & = & \frac{\mbox{Quoted Price}}{\mbox{Face Value}} \times 100\% \\ & = & \frac{5,527.57}{8,000} \times 100\% \\ & = & 69.09\%\end{eqnarray*}[/latex]
Step 7: Write as a statement.
The quoted price as a percentage of face value is [latex]69.09\%[/latex].
Try It
2) A [latex]15-[/latex]year, [latex]\$7,000[/latex] bond with a [latex]2.9\%[/latex] coupon was issued on September 1, 2015. The bond was purchased on April 15, 2023 when the yield to maturity was [latex]4.1\%[/latex]. Calculate the quoted price as a percentage of face value.
Solution
The four dates are
- Purchase date: April 15, 2023
- Maturity date: September 1, 2030
- Payment date before purchase date: March 1, 2023
- Payment date after purchase date: September [latex]1, 2023[/latex]
Calculate the market price on March 1, 2023.
[latex]\begin{eqnarray*} PMT & = & FV \times \frac{\mbox{coupon rate}}{2} \\ & = & 7,000\times \frac{0.029}{2}\\ & = & \$101.50\end{eqnarray*}[/latex]
| PMT Setting | END |
| [latex]N[/latex] | [latex]2 \times 7.5=15[/latex] |
| [latex]PV[/latex] | [latex]?[/latex] |
| [latex]FV[/latex] | [latex]7,000[/latex] |
| [latex]PMT[/latex] | [latex]101.50[/latex] |
| [latex]I/Y[/latex] | [latex]4.1[/latex] |
| [latex]P/Y[/latex] | [latex]2[/latex] |
| [latex]C/Y[/latex] | [latex]2[/latex] |
[latex]PV=\$6,462.34[/latex]
Calculate the flat price on April 15, 2023.
| [latex]N[/latex] | [latex]\frac{45}{184}[/latex] |
| [latex]PV[/latex] | [latex]6,462.34[/latex] |
| [latex]FV[/latex] | [latex]?[/latex] |
| [latex]PMT[/latex] | [latex]0[/latex] |
| [latex]I/Y[/latex] | [latex]4.1[/latex] |
| [latex]P/Y[/latex] | [latex]2[/latex] |
| [latex]C/Y[/latex] | [latex]2[/latex] |
[latex]FV=\$6,494.50[/latex]
Calculate the accrued interest.
[latex]\begin{eqnarray*}\mbox{Accrued Interest} & = & PMT \times \frac{\mbox{Number of days from March 1, 2023 to April 15, 2023}}{\mbox{Number of days from March 1, 2023 to September 1, 2023}} \\ & = & 101.50 \times \frac{45}{184} \\ & = & \$24.82 \end{eqnarray*}[/latex]
Calculate the quoted price.
[latex]\begin{eqnarray*} \mbox{Quoted Price} & = & \mbox{Flat Price}- \mbox{Accrued Interest} \\ & = & 6,494.50-24.82 \\ & = & \$6,469.68\end{eqnarray*}[/latex]
Calculate the quoted price as a percentage of face value.
[latex]\begin{eqnarray*} \mbox{Percent of Face Value} & = & \frac{\mbox{Quoted Price}}{\mbox{Face Value}} \times 100\% \\ & = & \frac{6,469.68}{7,000} \times 100\% \\ & = & 92.42\%\end{eqnarray*}[/latex]
Section 4.5 Exercises
- A [latex]\$50,000[/latex] bond with a [latex]6.33\%[/latex] coupon rate is redeemable on January 1, 2038. The bond was purchased on May 2, 2023 when the yield rate was [latex]4.19\%[/latex].
- Calculate the flat price on the purchase date.
- Calculate the quoted price on the purchase date.
- Calculate the quoted price as a percentage of face value on the purchase date.
Solution
a. [latex]\$62,689.98[/latex]; b. [latex]\$61,632.07[/latex]; c. [latex]123.26\%[/latex]
- A [latex]30-[/latex]year, [latex]\$2,500[/latex] bond with a [latex]10.4\%[/latex] coupon rate was issued on November 1, 2006. The bond was purchased on September 13, 2023 when the yield to maturity was [latex]12.39\%[/latex].
- Calculate the flat price on the purchase date.
- Calculate the quoted price on the purchase date.
- Calculate the quoted price as a percentage of face value on the purchase date.
Solution
a. [latex]\$2,275.89[/latex]; b. [latex]\$2,180.51[/latex]; c. [latex]87.22\%[/latex]
- A [latex]\$15,000[/latex] bond with a [latex]9.75\%[/latex] coupon was purchased on January 2, 2023 when the yield rate was [latex]10.1\%[/latex]. The bond matures on April 1, 2040.
- Calculate the flat price on the purchase date.
- Calculate the quoted price on the purchase date.
- Calculate the quoted price as a percentage of face value on the purchase date.
Solution
a. [latex]\$14,944.40[/latex]; b. [latex]\$14,570.74[/latex]; c. [latex]97.14\%[/latex]
- A [latex]20-[/latex]year, [latex]\$10,000[/latex] bond was issued on September 1, 2019 with a [latex]2\%[/latex] coupon. The bond was purchased on November 17, 2023 when the yield rate was [latex]5.25\%[/latex].
- Calculate the flat price on the purchase date.
- Calculate the quoted price on the purchase date.
- Calculate the quoted price as a percentage of face value on the purchase date.
Solution
a. [latex]\$6,582.90[/latex]; b. [latex]\$6,540.59[/latex]; c. [latex]130.81\%[/latex]
Attribution
“7.5 Quotation of Bonds” from Business and Financial Mathematics by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.
“14.1: Determining the Value of a Bond” from Business Math: A Step-by-Step Handbook (2021B) by J. Olivier and Lyryx Learning Inc. through a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License unless otherwise noted.

