1.5 The Rule of 70
How many years would it take the GDP to double if it grows at a constant rate of g? If we denote with Y0 the starting level of output, then we are looking for T, the number of years, such that
| (11) |
As the economy grows at a constant rate of g, the relationship between the initial output at t = 0 and the output at t = T is given by:
| (12) |
Substituting Equation (12) into Equation (11) yields:
| (13) |
To solve for T in Equation (13), take the logarithm of both sides of the equation and apply the power rule of logarithms to obtain:
| (14) |
Equation (14) is the “Rule of 70,” a useful approximation used by economists to make quick comparisons, where g is expressed in decimals. Table 4 shows the doubling time at several different growth rates.
| Annual growth rate of GDP | Doubling time (in years) |
| 0.5% | 140 |
| 1% | 70 |
| 2% | 35 |
| 3% | 23 |
| 4% | 18 |
| 5% | 14 |
The average annual growth rate in per capita real GDP for a developed economy is typically 2 to 3%. A developing economy can grow much faster because it can adopt technology, production practices, and institutions from developed economies. Using the rule of 70, a developed economy will double its output every 25 to 35 years. In contrast, China, a developing economy, has grown at a spectacular average rate of about 7% per year over the last 40 years, thus witnessing a doubling in its standard of living every decade.
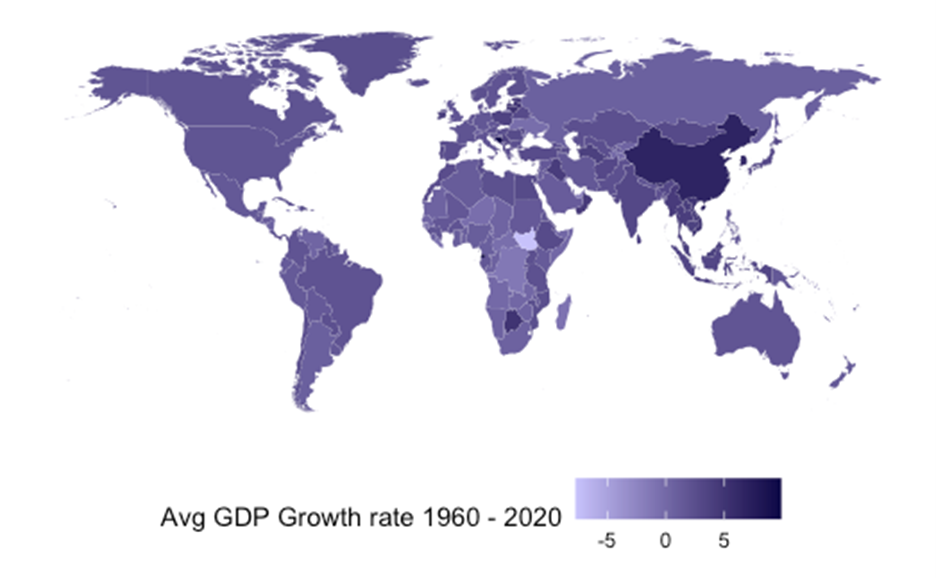
over the period 1960 – 2020. Data source: World Bank
Figure 1 shows the average growth rate over the post-World War II period around the globe. The darker the colour, the higher the growth rate. China’s “growth miracle” is an exception, even among developing countries. There are poor countries like Niger and Madagascar with negative average real growth rates over this 60-year period.
Economic growth is important for both rich and poor countries. Over time, small differences in growth rates accumulate to large differences in the standard of living because of the power of compound growth, which works very much the same way as compound interest. Thus, if policy makers can increase growth even by a tiny amount, this would translate into large differences in living standards over the long run.

