6 Classification

Si l’interprétation visuelle d’une image satellite peut suffire à certains usages, elle présente également des lacunes importantes. Par exemple, si vous voulez savoir où se trouvent toutes les zones urbaines d’une image, a) il faudra beaucoup de temps, même à un analyste d’images expérimenté, pour examiner une image entière et déterminer quels pixels sont « urbains » et lesquels ne le sont pas, et b) la carte des zones urbaines qui en résulte sera nécessairement quelque peu subjective, car elle est basée sur l’interprétation par l’analyste individuel de ce que signifie « urbain » et de la façon dont cela est susceptible d’apparaître sur l’image. Une solution très courante consiste à utiliser un algorithme de classification pour traduire la couleur observée dans chaque pixel en une classe thématique qui décrit sa couverture terrestre dominante, transformant ainsi l’image en une carte de couverture terrestre. Ce processus est appelé classification d’images.

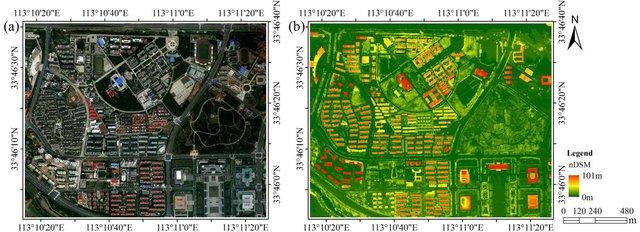
Figure 43: La classification des images traduit les couleurs de l’image originale (à gauche) en classes thématiques, généralement définies comme la couverture terrestre dominante ou l’utilisation des sols de chaque zone. WorldView-2 and LiDAR nDSM image of the study area (Figure 1) par Wu et al., CC BY 3.0.

On peut distinguer deux catégories d’approches de la classification des images. La méthode traditionnelle et la plus simple consistent à examiner chaque pixel individuellement et à déterminer la classe thématique correspondant à sa couleur. C’est ce qu’on appelle la classification par pixel, et c’est ce que nous allons voir en premier. Une méthode plus récente et de plus en plus populaire consiste à diviser l’image en segments homogènes, puis à déterminer la classe thématique correspondant aux attributs de chaque segment. Ces attributs peuvent être la couleur du segment ainsi que d’autres éléments comme la forme, la taille, la texture et l’emplacement. C’est ce qu’on appelle généralement l’analyse d’image basée sur l’objet, et nous y reviendrons dans la seconde moitié de ce chapitre.

Même dans la catégorie de la classification par pixel, deux approches différentes sont disponibles. La première est appelée classification « supervisée », car l’analyste d’images « supervise » la classification en fournissant des informations supplémentaires dans les premières étapes. L’autre est appelée classification « non supervisée », car un algorithme effectue la majeure partie du travail (presque) sans aide, et l’analyste d’images n’a plus qu’à intervenir à la fin pour terminer le travail. Chacune de ces méthodes présente des avantages et des inconvénients, qui sont décrits ci-après.

Classification supervisée par pixel

L’idée derrière la classification supervisée est que l’analyste de l’image fournit à l’ordinateur certaines informations qui permettent de calibrer un algorithme de classification. Cet algorithme est ensuite appliqué à chaque pixel de l’image pour produire la carte requise. La meilleure façon d’expliquer ce fonctionnement est de prendre un exemple. L’image de la figure 44 provient de Californie, et nous voulons traduire cette image en une classification comportant les trois (grandes) classes suivantes : « Urbain », « Végétation » et « Eau ». Le nombre de classes et la définition de chaque classe peuvent avoir un impact important sur le succès de la classification. Dans notre exemple, nous ne tenons pas compte du fait qu’une grande partie de la zone est constituée de sol nu (et n’entre donc pas vraiment dans l’une de nos trois classes). Nous pouvons également nous rendre compte que l’eau dans l’image a une couleur très différente selon son degré de turbidité, et que certaines zones urbaines sont très claires alors que d’autres sont d’un gris plus foncé, mais nous ignorons ces questions pour l’instant.

Figure 44: Composite en couleurs vraies montrant une partie d’une image Landsat de Californie. Une zone urbaine avec de l’eau trouble est visible dans le coin supérieur droit, bordée par un mélange de zones de végétation et de zones stériles et un lac avec de l’eau claire. Une zone montagneuse largement boisée est visible dans la partie inférieure gauche de l’image, avec quelques zones claires près du centre gauche. Par Anders Knudby, CC BY 4.0, basé sur une image Landsat 5 (USGS).

La « supervision » dans la classification supervisée se présente presque toujours sous la forme d’un ensemble de données de calibrage, qui consiste en un ensemble de points et/ou de polygones dont on sait (ou croit) qu’ils appartiennent à chaque classe. Dans la figure 45, un tel ensemble de données a été fourni sous la forme de trois polygones. Le polygone rouge délimite une zone connue pour être « urbaine », de même le polygone bleu est « eau » et le polygone vert est « végétation ». Notez que l’exemple de la figure 45 n’est pas un exemple de bonne pratique — il est préférable d’avoir des polygones plus nombreux et plus petits pour chaque classe, répartis sur l’ensemble de l’image, car cela permet aux polygones de couvrir que les pixels de la classe voulue, et aussi d’intégrer les variations spatiales, par exemple la densité de la végétation, la qualité de l’eau, etc.

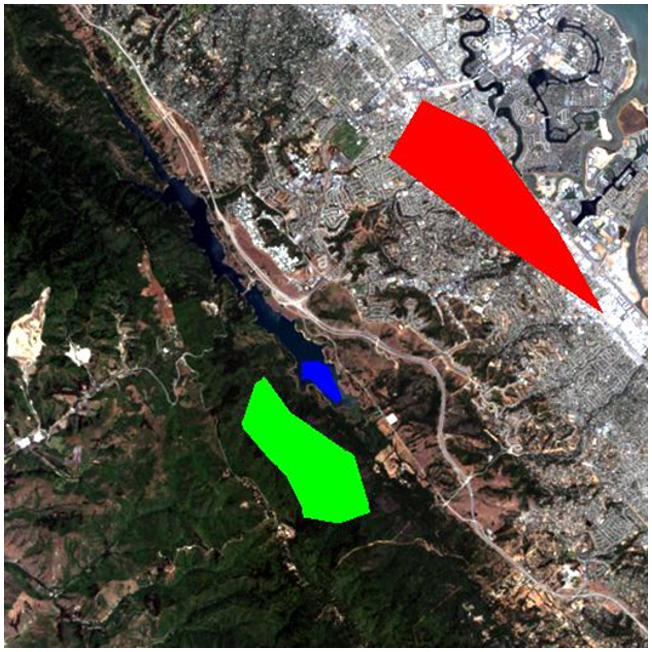
Figure 45: La même image que dans la Figure 44, avec trois polygones superposés. Le polygone rouge représente une zone connue par l’analyste de l’image comme étant « urbaine », le polygone bleu est « eau », et le polygone vert est « végétation ». Par Anders Knudby, CC BY 4.0.

Regardons maintenant comment ces polygones nous aident à transformer l’image en une carte des trois classes. En gros, les polygones disent à l’ordinateur « regardez les pixels sous le polygone rouge – c’est à cela que ressemblent les pixels “urbains” », et l’ordinateur peut alors trouver tous les autres pixels de l’image qui ressemblent aussi à cela, et les étiqueter « urbains ». Et ainsi de suite pour les autres classes. Cependant, certains pixels peuvent ressembler un peu à « urbain » et un peu à « végétation », il faut donc trouver un moyen mathématique de déterminer à quelle classe chaque pixel ressemble le plus. Nous avons besoin d’un algorithme de classification.

Si nous prenons toutes les valeurs de tous les pixels des bandes 3 et 4 de Landsat et les montrons sur un nuage de points, nous obtenons quelque chose comme la figure 46. Cette image a une résolution radiométrique de 8 bits, donc les valeurs de chaque bande vont théoriquement de 0 à 255, nous observons que les plus petites valeurs de l’image sont supérieures à 0. Les valeurs de la bande 3 sont représentées sur l’axe des x, et celles de la bande 4 sur l’axe des y.

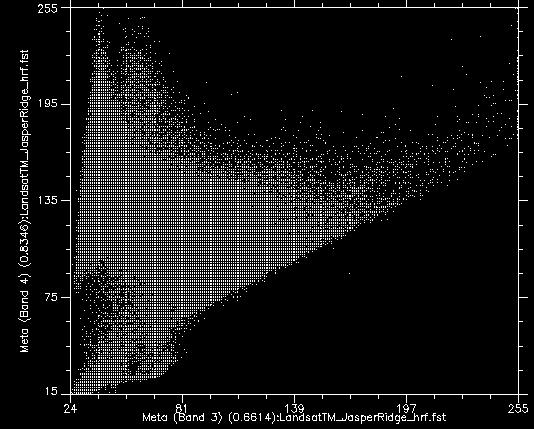
Figure 46: Nuage de points montrant toutes les valeurs de pixels dans les bandes 3 et 4 pour l’image de la Figure 44. Nuage de points créé à l’aide du logiciel ENVI. Par Anders Knudby, CC BY 4.0.

Maintenant, si nous colorions tous les points qui proviennent des pixels sous le polygone rouge (c’est-à-dire les pixels que nous « savons » être « Urbains »), et que nous faisons de même avec les pixels sous les polygones bleus et verts, nous obtenons quelque chose comme la figure 47. Il y a quelques éléments importants à noter dans la figure 47. Tous les points bleus (« Eau ») se trouvent dans le coin inférieur gauche de la figure, sous le cercle jaune, avec de faibles valeurs dans la bande 3 et de faibles valeurs dans la bande 4. C’est en effet typique de l’eau, car l’eau absorbe très efficacement le rayonnement entrant dans les longueurs d’onde du rouge (bande 3) et du proche infrarouge (bande 4), de sorte que très peu sont réfléchis pour être détectés par le capteur. Les points verts (« végétation ») forment une longue zone sur le côté gauche de la figure, avec des valeurs faibles dans la bande 3 et des valeurs modérées à élever dans la bande 4. Là encore, cela semble raisonnable, car la végétation absorbe efficacement le rayonnement entrant dans la bande rouge (en l’utilisant pour la photosynthèse) tout en réfléchissant le rayonnement entrant dans la bande du proche infrarouge. Les points rouges (« Urbain ») forment une zone plus large près du centre de la figure, et couvrent une gamme de valeurs beaucoup plus large que les deux autres classes. Si leurs valeurs sont similaires à celles de la « Végétation » dans la bande 4, elles sont généralement plus élevées dans la bande 3.

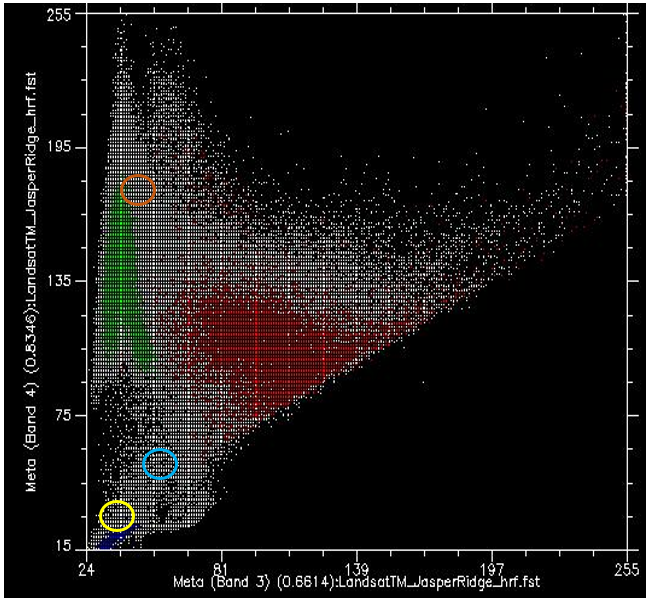
Figure 47: Comme la Figure 46, mais avec chaque point coloré par le polygone sous lequel il se trouve. Nuage de points créé à l’aide du logiciel ENVI. Par Anders Knudby, CC BY 4.0.

Ce que nous voulons que l’algorithme de classification supervisée fasse maintenant, c’est prendre tous les autres pixels de l’image (c’est-à-dire tous les points blancs sur le nuage de points) et les affecter à l’une des trois classes en fonction de leur couleur. Par exemple, à quelle classe pensez-vous que les points blancs dans le cercle jaune de la figure 47 devraient être affectés ? L’eau, probablement. Et qu’en est-il de ceux qui se trouvent dans le cercle marron clair ? Végétation, probablement. Mais qu’en est-il de ceux dans le cercle bleu clair ? Pas si facile à déterminer.

Remarque : l’algorithme de classification peut utiliser toutes les bandes de l’image Landsat, ainsi que toute autre information que nous fournissons pour l’ensemble de l’image (comme un modèle numérique d’altitude), mais comme il est plus facile de continuer à représenter cette image en deux dimensions en utilisant uniquement les bandes 3 et 4, nous allons continuer à le faire. Gardez à l’esprit que le nuage de points est en réalité un graphique à n dimensions, où n est égal au nombre de bandes (et autres couches de données) que nous voulons utiliser dans la classification.

Classificateur à distance minimale

Une façon d’estimer à quelle classe appartient chaque pixel est de calculer la « distance » entre le pixel et le centre de tous les pixels connus pour appartenir à chaque classe, puis de l’affecter à la classe la plus proche. Par « distance », nous entendons ici la distance dans « l’espace caractéristique », dans lequel les dimensions sont définies par chacune des variables que nous considérons (dans notre cas, les bandes 3 et 4), par opposition à la distance physique. Notre espace caractéristique est donc bidimensionnel, et les distances peuvent être calculées à l’aide d’une distance euclidienne standard.

Par exemple, pour les points de la figure 48, nous avons calculé les valeurs moyennes de tous les pixels verts, rouges et bleus pour les bandes 3 et 4, et que nous avons indiquées par de gros points. Disons qu’ils ont les valeurs suivantes :

Tableau 3: Les valeurs moyennes dans les bandes 3 et 4 pour les classes « Urbain », « Végétation » et « Eau » sont présentées dans la Figure 49.

Disons ensuite qu’un pixel indiqué par le point jaune de la figure 48 a une valeur de 55 dans la bande 3, et de 61 dans la bande 4. Nous pouvons alors calculer la distance euclidienne entre ce point et la valeur moyenne de chaque classe  :

Distance à la moyenne rouge : (100-55)²+(105-61)² = 62.9

Distance à la moyenne verte : (40-55)²+(135-61)² = 75.5

Distance à la moyenne bleue : (35-55)²+(20-61)² = 45.6

minimale affectera ce point particulier à la classe « bleu ». Bien que le classificateur de distance minimale soit très simple et rapide et qu’il donne souvent de bons résultats, cet exemple illustre une faiblesse importante : dans notre exemple, la distribution des valeurs pour la classe « Eau » est très faible — l’eau est en principe toujours foncé et bleu vert, et même l’eau trouble ou l’eau contenant beaucoup d’algues a toujours l’air foncée et bleue — verte. La distribution des valeurs pour la classe « Végétation » est beaucoup plus importante, surtout dans la bande 4, parce que certaines végétations sont denses et d’autres ne le sont pas, certaines végétations sont saines et d’autres ne le sont pas, certaines végétations peuvent être mélangées avec des sols sombres, des sols clairs, ou même des éléments urbains comme une route. Il en va de même pour la classe « urbaine », qui présente une large distribution de valeurs dans les bandes 3 et 4. En réalité, le point jaune de la figure 48 n’est probablement pas de l’eau, car l’eau qui a des valeurs aussi élevées dans les bandes 3 et 4 n’existe pas. Il est beaucoup plus probable qu’il s’agisse d’un type de végétation inhabituel, d’une zone urbaine inhabituelle ou (plus probablement encore) d’un mélange de ces deux classes. Le prochain classificateur que nous allons examiner prend explicitement en compte la distribution des valeurs dans chaque classe, pour remédier à ce problème.

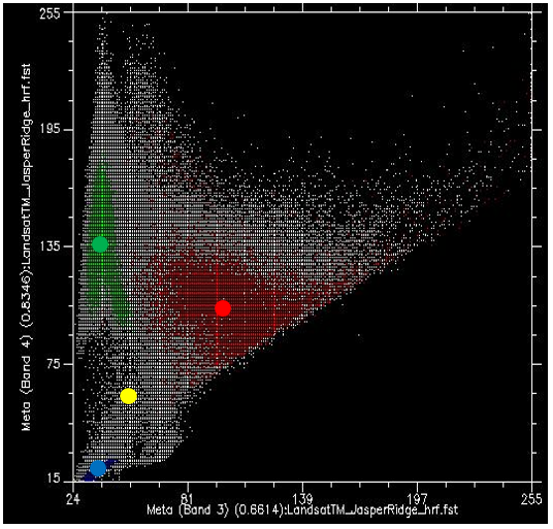
Figure 48: Le classificateur de distance minimale attribue la classe dont le centre est le plus proche (dans l’espace des caractéristiques) de chaque pixel. La valeur moyenne de tous les points rouges, dans les bandes 3 et 4, est indiquée par le gros point rouge, de même pour les points verts et bleus. Le point jaune indique un pixel que nous souhaitons attribuer à l’une des trois classes. Diagramme de dispersion créé à l’aide du logiciel ENVI. Par Anders Knudby, CC BY 4.0.

Classificateur à maximum de vraisemblance

Jusqu’à il y a une dizaine d’années, le classificateur de vraisemblance maximale était l’algorithme de référence pour la classification d’images. Il est toujours populaire, implémenté dans tous les logiciels de télédétection sérieux et figure généralement parmi les algorithmes les plus performants pour une tâche donnée. Les descriptions mathématiques de son fonctionnement peuvent sembler compliquées, car elles reposent sur des statistiques bayésiennes appliquées à plusieurs dimensions, mais le principe est relativement simple : au lieu de calculer la distance au centre de chaque classe (dans l’espace des caractéristiques) et donc de trouver la classe la plus proche, nous allons calculer la probabilité que le pixel appartienne à chaque classe, et donc trouver la classe la plus probable. Pour que ce calcul fonctionne, il faut faire quelques hypothèses.

• Nous supposerons qu’avant de connaître la couleur du pixel, la probabilité qu’il appartienne à une classe est la même que la probabilité qu’il appartienne à toute autre classe. Cela semble assez raisonnable (bien que dans notre image il y ait clairement beaucoup plus de « végétation » que d’ « eau », on pourrait donc dire qu’un pixel de couleur inconnue a plus de chances d’être de la végétation que de l’eau… cela peut être incorporé dans le classificateur, mais c’est très rare, et nous l’ignorerons pour l’instant).
• Nous supposerons que la distribution des valeurs dans chaque bande et pour chaque classe est gaussienne, c’est-à-dire qu’elle suit une distribution normale (une courbe en cloche).

Pour commencer par un exemple unidimensionnel, notre situation pourrait ressembler à ceci si nous n’avions que deux classes :

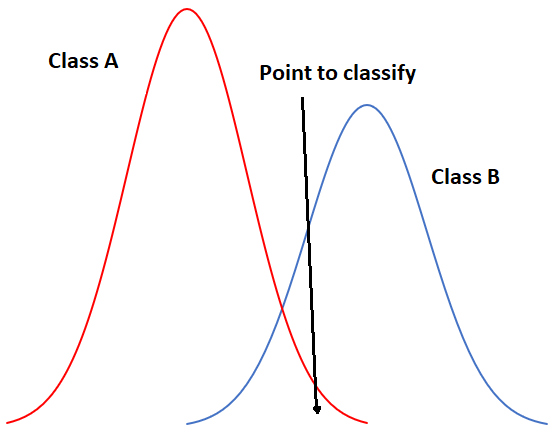
Figure 49: Exemple unidimensionnel de classification par maximum de vraisemblance avec deux classes. Par Anders Knudby, CC BY 4.0.

Dans la figure 49, l’axe des x représente les valeurs dans une bande d’images, et l’axe des y montre le nombre de pixels dans chaque classe qui a une valeur donnée dans cette bande. Il est clair que la classe A présente généralement des valeurs faibles, et la classe B des valeurs élevées, mais la distribution des valeurs dans chaque bande est suffisamment importante pour qu’il y ait un certain chevauchement entre les deux. Les deux distributions étant gaussiennes, nous pouvons calculer à la fois la moyenne et l’écart type pour chaque classe, puis calculer le z-score (combien d’écarts types nous séparent de la moyenne). Dans la figure 49, les deux classes ont le même écart type (les « cloches » ont la même « largeur »), et parce que le point est situé un peu plus près de la moyenne de la classe B que de la classe A, son score z serait le plus faible pour la classe B et il serait affecté à cette classe. Un exemple légèrement plus réaliste est fourni ci-dessous dans la figure 50, où nous avons deux dimensions et trois classes. Les écarts types de la bande 4 (axe des x) et de la bande 3 (axe des y) sont représentés sous forme de contours d’équiprobabilité. Dans ce cas, le défi pour le classificateur à maximum de vraisemblance est de trouver la classe pour laquelle le point se trouve dans le contour d’équiprobabilité au plus proche du centre de la classe. Voyez par exemple que les contours des classes A et B se chevauchent, et que les écarts types de la classe A sont plus grands que ceux de la classe B. Par conséquent, le point rouge est plus proche (dans l’espace des caractéristiques) du centre de la classe B que du centre de la classe A, mais il se trouve sur le troisième contour d’équiprobabilité de la classe B et sur le deuxième de la classe A. Le classificateur de distance minimale classerait ce point dans la « classe B » sur la base de la distance euclidienne la plus courte, tandis que le classificateur de vraisemblance maximale le classerait dans la « classe A » en raison de sa plus grande probabilité d’appartenir à cette classe (selon les hypothèses utilisées). Qu’est-ce qui a le plus de chances d’être correct ? La plupart des comparaisons entre ces classificateurs suggèrent que le classificateur de vraisemblance maximale a tendance à produire des résultats plus précis, mais cela ne garantit pas qu’il soit toujours supérieur.

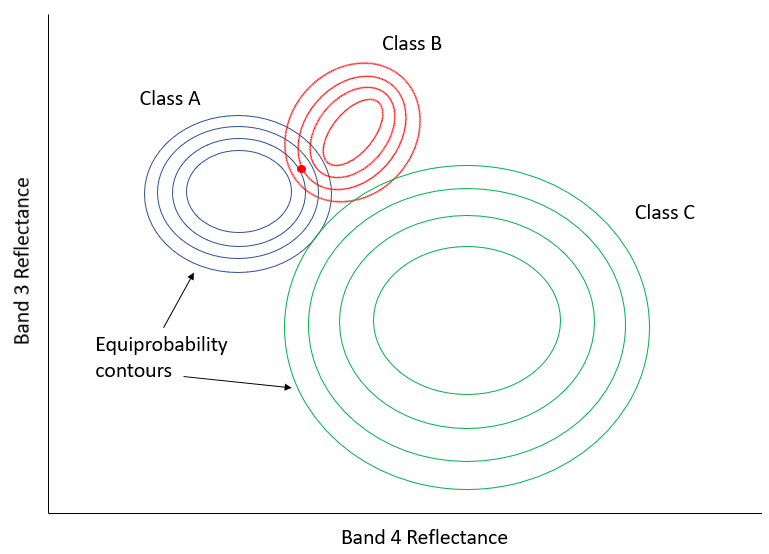
Figure 50: Exemple bidimensionnel de la situation de classification par maximum de vraisemblance, avec six classes qui ont des distributions standard inégales. Par Anders Knudby, CC BY 4.0.

Classificateurs non paramétriques

Au cours des dernières années, les scientifiques de la télédétection se sont de plus en plus tournés vers le domaine de l’apprentissage automatique pour adopter de nouvelles techniques de classification. L’idée de la classification est fondamentalement très générique : vous disposez de données sur quelque chose (dans notre cas, les valeurs des bandes d’un pixel) et vous voulez savoir de quoi il s’agit (dans notre cas, quelle est la couverture terrestre). Un problème peut difficilement être plus générique, si bien que l’on en trouve des versions partout : une banque dispose de certaines informations sur un client (âge, sexe, adresse, revenus, historique de remboursement des prêts) et veut savoir s’il doit être considéré comme un « faible risque », un « risque moyen » ou un « risque élevé » pour un nouveau prêt de 100 000 dollars. Un météorologue dispose d’informations sur le temps actuel (« pluie, 5 °C ») et sur les variables atmosphériques (« 1003 mb, 10 m/s de vent du NW »), et doit déterminer s’il pleuvra ou non dans trois heures. Un ordinateur dispose de certaines informations sur les empreintes digitales trouvées sur une scène de crime (longueur, courbure, position relative de chaque ligne) et doit déterminer s’il s’agit des vôtres ou de celles d’un tiers.) Parce que la tâche est générique, et parce que les utilisateurs en dehors du domaine de la télédétection disposent de grandes quantités d’argent et peuvent utiliser les algorithmes de classification pour générer des profits, les informaticiens ont développé de nombreuses techniques pour résoudre cette tâche générique, et certaines de ces techniques ont été adoptées en télédétection. Nous allons examiner un seul exemple ici, mais n’oubliez pas qu’il existe de nombreux autres algorithmes de classification génériques qui peuvent être utilisés en télédétection.

Celui que nous allons examiner s’appelle un classificateur à arbre de décision. Comme les autres classificateurs, le classificateur à arbre de décision fonctionne selon un processus en deux étapes : 1) calibrer l’algorithme de classification, et 2) l’appliquer à tous les pixels de l’image. Un classificateur à arbre de décision est calibré en divisant récursivement l’ensemble des données (tous les pixels sous les polygones de la figure 45) pour maximiser l’homogénéité des deux parties (appelées nœuds). Une petite illustration : disons que nous avons 7 points de données (vous ne devriez jamais avoir seulement sept points de données lorsque vous calibrez un classificateur, ce petit nombre est utilisé uniquement à des fins d’illustration !)

Tableau 4: Sept points de données utilisés pour développer un classificateur à arbre de décision.

Data point	Band 1 value	Band 2 value	Actual class
1	10	30	A
2	20	40	A
3	30	40	A
4	15	55	B
5	35	40	B
6	40	35	B
7	45	35	B

La première tâche consiste à trouver une valeur, soit dans la bande 1, soit dans la bande 2, qui peut être utilisée pour diviser l’ensemble de données en deux nœuds de sorte que, dans la mesure du possible, tous les points de la classe A se trouvent dans un nœud et tous les points de la classe B dans l’autre. D’un point de vue algorithmique, cela se fait en testant toutes les valeurs possibles et en quantifiant l’homogénéité des classes résultantes. Ainsi, nous pouvons observer que la plus petite valeur dans la bande 1 est 10, et la plus grande est 45. Si nous divisons l’ensemble de données selon la règle suivante : « Tous les points dont la bande 1 est inférieure à 11 vont au nœud X, et tous les autres au nœud y », nous obtiendrons des points divisés comme suit :

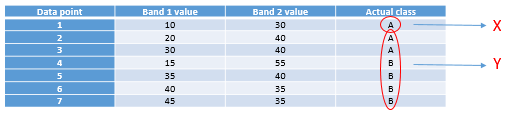
Figure 51: Répartition des points selon la valeur seuil 11 dans la bande 1. Par Anders Knudby, CC BY 4.0.

Comme nous pouvons le voir, cela nous laisse avec un seul point « A » dans un nœud (X), et deux points « A » et quatre points « B » dans l’autre nœud (Y). Pour savoir si nous pouvons faire mieux, nous pouvons essayer d’utiliser la valeur 12 au lieu de 11 (ce qui nous donne le même résultat), 13 (toujours le même), et ainsi de suite, et lorsque nous avons testé toutes les valeurs de la bande 1, nous continuons avec toutes les valeurs de la bande 2. Finalement, nous trouverons qu’utiliser la valeur 31 dans la bande 1 nous donne le résultat suivant  :

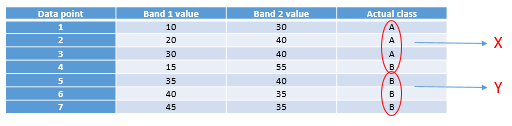
Figure 52: Points crachés selon la valeur seuil 31 dans la bande 1. Par Anders Knudby, CC BY 4.0.

C’est presque parfait, sauf que nous avons un seul « B » dans le nœud X. Mais bon, c’est plutôt bien pour un premier partage. Nous pouvons représenter cela sous forme d’un « arbre » comme ceci :

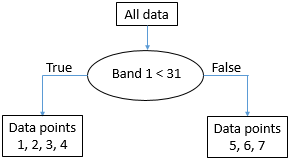
Figure 53: La structure « arborescente » qui émerge de la division des données sur la valeur seuil 31 dans la bande 1. Chaque ensemble de points de données est appelé un nœud. Le « nœud racine » contient tous les points de données. Les « nœuds feuilles », également appelés « nœuds terminaux », sont les points finaux. Par Anders Knudby, CC BY 4.0.

Le nœud avec les points de données 5, 6 et 7 (qui ont tous des valeurs de bande 1 supérieures à 31) est maintenant ce qu’on appelle un « nœud pur » — il est composé de points de données d’une seule classe, nous n’avons donc plus besoin de le diviser. Les nœuds qui sont des points terminaux sont également appelés « feuilles ». Le nœud avec les points de données 1, 2, 3 et 4 n’est pas « pur », car il contient un mélange de points de classe A et de classe B. Nous recommençons donc à tester toutes les différentes valeurs possibles que nous pouvons utiliser comme seuil pour diviser ce nœud (et seulement ce nœud), dans les deux bandes. Il se trouve que le point de la classe B dans ce nœud a une valeur dans la bande 2 qui est plus élevée que tous les autres points, donc une valeur de séparation de 45 fonctionne bien, et nous pouvons mettre à jour l’arbre comme ceci  :

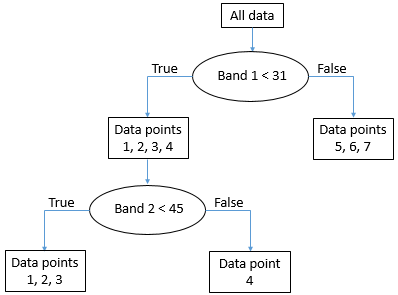
Figure 54: La structure « arborescente » finale. Tous les nœuds (parties finales de l’ensemble de données) sont maintenant purs. Par Anders Knudby, CC BY 4.0.

Une fois que «  l’arbre »   est en place, nous pouvons maintenant prendre tous les autres pixels de l’image et les faire « tomber » dans l’arbre pour voir dans quelle feuille ils atterrissent. Par exemple, un pixel ayant des valeurs de 35 dans la bande 1 et de 25 dans la bande 2 « ira à droite » au premier test et atterrira donc dans la feuille qui contient les points de données 5, 6 et 7. Comme tous ces points appartiennent à la classe B, ce pixel sera classé dans la classe B. Et ainsi de suite.

Notez que les feuilles ne doivent pas nécessairement être « pures », certains arbres cessent de diviser les nœuds lorsqu’ils sont inférieurs à une certaine taille, ou en utilisant un autre critère. Dans ce cas, un pixel atterrissant dans une telle feuille se verra attribuer la classe qui compte le plus de points dans cette feuille (et l’information selon laquelle il ne s’agissait pas d’une feuille pure peut même être utilisée pour indiquer que la classification de ce pixel particulier est sujette à une certaine incertitude).

Le classificateur à arbre de décision n’est qu’un des nombreux exemples possibles de classificateurs non — paramétriques. Il est rarement utilisé directement sous la forme présentée ci-dessus, mais il constitue la base de certains des algorithmes de classification les plus performants utilisés aujourd’hui. D’autres algorithmes de classification non paramétriques populaires incluent les réseaux neuronaux et les machines à vecteurs de support, qui sont tous deux implémentés dans de nombreux logiciels de télédétection.

Classification non supervisée par pixel

Que faire si nous ne disposons pas des données nécessaires pour calibrer un algorithme de classification ? Si nous n’avons pas les polygones illustrés à la figure 45, ou les points de données indiqués au tableau 4 ? Que faisons-nous alors ? Nous utilisons une classification non supervisée à la place !

La classification non supervisée consiste à laisser un algorithme diviser les pixels d’une image en « clusters naturels », c’est-à-dire en combinaisons de valeurs de bandes que l’on retrouve fréquemment dans l’image. Une fois ces groupes naturels identifiés, l’analyste d’images peut alors les étiqueter, en se basant généralement sur une analyse visuelle de l’emplacement de ces groupes dans l’image. Le regroupement est en grande partie automatique, bien que l’analyste fournisse quelques paramètres initiaux. L’un des algorithmes les plus couramment utilisés pour trouver des groupes naturels dans une image est l’algorithme K-Means, qui fonctionne comme suit  :

1) L’analyste détermine le nombre souhaité de classes. Fondamentalement, si vous voulez une carte avec un haut niveau de détail thématique, vous pouvez définir un grand nombre de classes. Notez également que les classes peuvent être combinées ultérieurement, il est donc souvent judicieux de fixer le nombre de classes souhaitées à un niveau légèrement supérieur à celui que vous pensez serait votre résultat de la fin. Un nombre de points « d’amorçage » égal au nombre de classes souhaité est ensuite placé de manière aléatoire dans l’espace des caractéristiques.

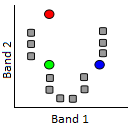
Figure 55: Classification K-Means étape 1. Un certain nombre de points « d’amorçage » (points colorés) sont distribués aléatoirement dans l’espace des caractéristiques. Les points gris représentent ici les pixels à regrouper. Modifié à partir de K Means Example Step 1 par Weston.pace, Wikimedia Commons, CC BY-SA 3.0.

2) Des clusters sont ensuite générés autour des points « graines » en attribuant tous les autres points à la graine la plus proche.

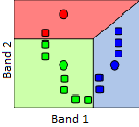
Figure 56: Un cluster est formé autour de chaque graine en attribuant tous les points à la graine la plus proche. Modifié à partir de K Means Example Step 2 par Weston.pace, Wikimedia Commons, CC BY-SA 3.0.

3) Le centroïde (centre géographique) des points de chaque groupe devient la nouvelle « graine ».

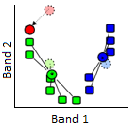
Figure 57: Les graines sont déplacées vers le centroïde de chaque grappe. Le centroïde est calculé comme le centre géographique de chaque grappe, c’est-à-dire qu’il est situé à la valeur x moyenne de tous les points de la grappe, et à la valeur y moyenne de tous les points de la grappe. Modifié à partir de K Means Example Step 3 par Weston.pace, Wikimedia Commons, CC BY-SA 3.0.

4) Répétez les étapes 2 et 3 jusqu’au critère d’arrêt. Le critère d’arrêt peut être qu’aucun point ne se déplace vers un autre cluster, ou que le centroïde de chaque cluster se déplace de moins d’une distance préspécifiée, ou qu’un certain nombre d’itérations ont été complétées.

D’autres algorithmes de classification non supervisée effectuent le regroupement de manière légèrement différente. Par exemple, un algorithme populaire appelé ISODATA permet également la division de grands clusters pendant le processus de clustering, et de la même manière la fusion de petits clusters proches. Néanmoins, le résultat de l’algorithme de clustering est que chaque pixel de l’image entière fait partie d’un cluster. L’espoir est donc que chaque cluster représente un type d’occupation du sol qui peut être identifié par l’analyste d’images, par exemple en superposant l’emplacement de tous les pixels du cluster sur l’image originale pour identifier visuellement ce à quoi correspond ce cluster. C’est l’étape finale de la classification non supervisée — l’étiquetage de chacun des clusters qui ont été produits. C’est l’étape où il peut être pratique de fusionner des clusters, si par exemple vous avez un cluster qui correspond à une eau trouble et un autre qui correspond à une eau claire. À moins que vous ne soyez spécifiquement intéressé par la qualité de l’eau, différencier les deux n’est probablement pas important, et les fusionner fournira un produit cartographique plus clair. De même, il se peut que vous ayez simplement deux grappes qui semblent toutes deux correspondre à une forêt feuillue saine. Même si vous travaillez pour un service forestier, à moins que vous ne puissiez déterminer avec certitude quelle est la différence entre ces deux groupements, vous pouvez les fusionner en un seul et les appeler « forêt de feuillus ».

À titre d’exemple, l’image ci-dessous montre l’image originale en arrière-plan, et les pixels centraux colorés selon le produit d’une classification non supervisée. Il est clair que la zone « bleue » correspond aux pixels recouverts d’eau, et que la zone verte correspond en grande partie à la végétation. Une analyse plus détaillée de l’image serait nécessaire pour étiqueter chaque zone, en particulier les zones rouges et grises, de manière appropriée.

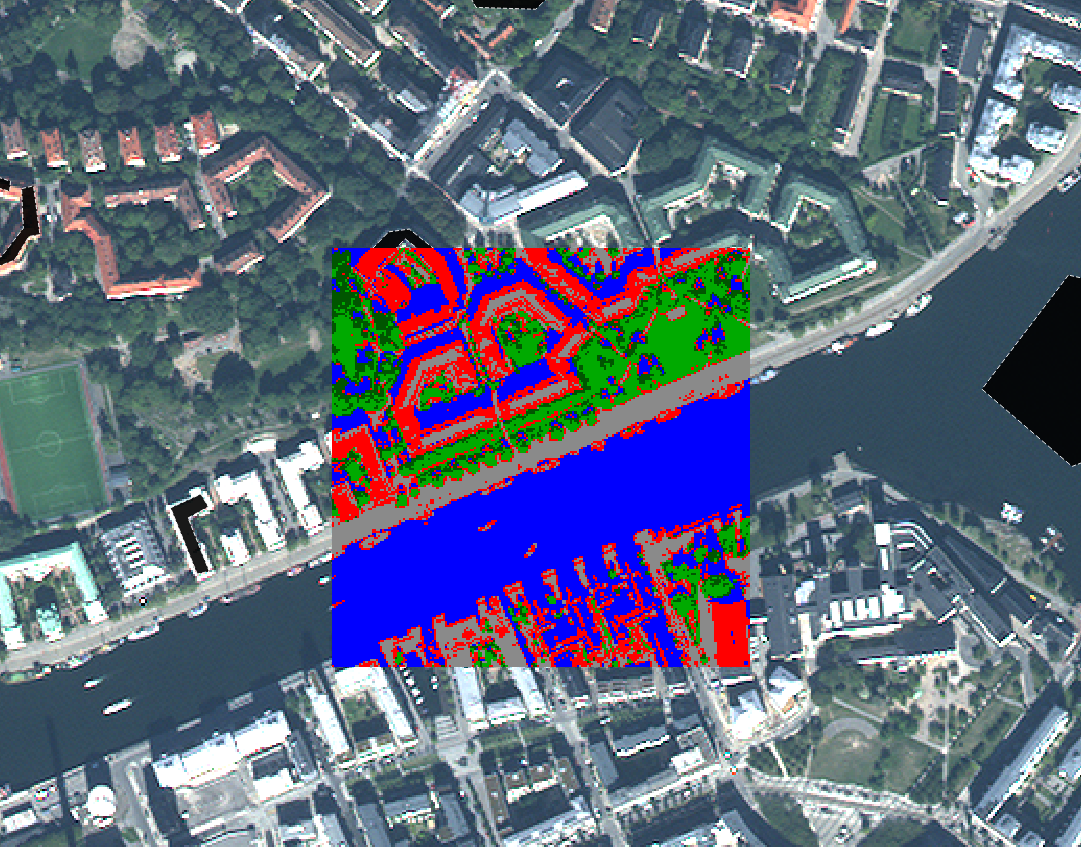
Figure 58: Exemple de correspondance entre l’image originale et les clusters formés dans un processus de classification non supervisé. Par Anders Knudby, CC BY 4.0.

La classification de l’occupation du sol est l’une des plus anciennes utilisations de la télédétection, et c’est quelque chose que de nombreux gouvernements nationaux font régulièrement pour leur territoire. Par exemple, au Canada, le Centre canadien de télédétection travaille avec des partenaires des États-Unis et du Mexique pour créer une carte de la couverture terrestre nord-américaine. Des cartes mondiales d’occupation du sol sont également produites par divers établissement, comme l’USGS, l’Université du Maryland, l’ESA et la Chine, pour n’en citer que quelques-unes.

L’un des défauts typiques des systèmes de classification d’images qui fonctionnent au niveau du pixel par pixel est que les images sont bruyantes, et que les cartes d’occupation du sol réalisées à partir d’images héritent de ce bruit. Un autre défaut plus important est qu’il y a de l’information dans une image au-delà de ce que l’on trouve dans les pixels individuels. Une image est l’illustration parfaite du dicton « le tout est plus grand que la somme de ses parties », car les images ont une structure, et la structure n’est pas prise en compte lorsqu’on regarde chaque pixel indépendamment du contexte fourni par tous les pixels voisins. Par exemple, même sans connaître la couleur d’un pixel, si je sais que tous ses pixels voisins sont classés comme « eau », je peux dire avec une grande confiance que le pixel en question est aussi « eau ». J’aurai tort à l’occasion, mais j’aurai raison la plupart du temps. Nous allons maintenant nous pencher sur une technique appelée analyse d’image basée sur l’objet, qui tient compte du contexte lorsqu’elle génère des classifications d’images. Cet avantage lui permet souvent de surpasser les méthodes plus traditionnelles de classification pixel par pixel.

Analyse d’images basée sur les objets (OBIA)

Beaucoup de nouvelles avancées dans le monde de la télédétection proviennent du côté matériel des choses. Un nouveau capteur est lancé, et il a une meilleure résolution spatiale ou spectrale que les capteurs précédents, ou il produit des images moins bruyantes, ou il est mis gratuitement à disposition alors que les autres solutions étaient payantes. Les drones sont un autre exemple : le type d’images qu’ils produisent n’est pas très différent de ce qui était auparavant disponible avec les caméras des avions pilotés — en fait, leur qualité est souvent inférieure — mais le faible coût des drones et la facilité avec laquelle ils peuvent être déployés par des non-experts ont créé une révolution en matière de quantité d’images disponibles à basse altitude et de coût d’obtention d’images à haute résolution pour un petit site.

Le développement de l’analyse d’images basée sur les objets (en anglais « Object-Based Image Analysis », OBIA) est l’une des rares avancées substantielles du côté des logiciels. Le principe fondamental de l’OBIA est de considérer qu’une image est composée d’objets plutôt que de pixels. L’un des avantages de ce principe est que les gens ont tendance à voir le monde comme étant composés d’objets, et non de pixels, de sorte qu’une analyse d’image qui adopte le même point de vue produit des résultats qui sont plus facilement interprétés par les gens. Par exemple, lorsque vous regardez la figure 59, vous pouvez probablement voir le visage d’un homme (si vous le connaissez, vous reconnaîtrez également qui est cet homme).

Figure 59: Robert De Niro. Ou, si vous utilisez un logiciel d’analyse d’images basé sur les pixels, une trame à trois bandes comportant 1556 colonnes et 2247 lignes, chaque pixel et chaque bande affichant un niveau de luminosité variable. Robert De Niro KVIFF portrait par Petr Novák (che), Wikimedia Commons, CC BY-SA 2.5.

Comme il s’agit d’une image numérique, nous savons qu’elle est en fait composée d’un certain nombre de pixels disposés proprement en colonnes et en rangées, et que la luminosité (c’est-à-dire l’intensité de la couleur rouge, verte et bleue de chaque pixel) peut être représentée par trois nombres. Nous pourrions donc classer les parties claires de l’image comme « peau » et les parties moins claires comme « autres », une classe mixte comprenant les yeux, les cheveux, les ombres et le fond. Mais ce n’est pas une classification particulièrement utile ou important ! Ce qui serait plus important serait de classer l’image en classes telles que « œil », « main », « cheveux », « nez », etc.

Un exemple un peu plus pertinent pour la télédétection est présenté ci-dessous à la figure 60, dans laquelle une zone urbaine a été classée en objets, notamment un stade facilement reconnaissable, des rues, des bâtiments individuels, de la végétation, etc.

Figure 60: Classification d’une zone urbaine à l’aide d’une analyse d’images basée sur les objets. Object based image analysis par Uddinkabir, Wikimedia Commons, CC BY-SA 4.0.

La segmentation d’image

Le but de la segmentation d’image est de prendre tous les pixels de l’image et de les diviser en segments — des parties contiguës de l’image qui ont une couleur similaire. La segmentation d’image est utile parce qu’elle nous évite d’analyser l’image pixel par pixel et nous permet d’analyser les segments individuels. Cette méthode présente plusieurs avantages très importants. Tout d’abord, nous pouvons examiner la « couleur moyenne » d’un segment et l’utiliser pour classer ce segment, plutôt que d’utiliser la couleur de chaque pixel individuel pour classer ce pixel. Si nous avons affaire à une imagerie bruyante (et c’est toujours le cas !), l’utilisation des moyennes de segments réduit l’influence du bruit sur la classification. Deuxièmement, les segments ont un certain nombre d’attributs qui peuvent être considérables et peuvent être utilisés pour aider à les classer — des attributs que les pixels n’ont pas. Par exemple, un segment d’image est constitué d’un certain nombre de pixels, et nous pouvons donc quantifier sa taille. Comme tous les segments n’ont pas la même taille, l’attribut « taille du segment » contient des informations qui peuvent être utilisées pour aider à classer les segments. Par exemple, dans la figure 60, remarquez que le segment couvrant le lac est assez grand par rapport à tous les segments terrestres. Cela s’explique par le fait que le lac est une partie très homogène de l’image. La même différence est observée entre les différentes parties de la zone terrestre — les segments situés juste à l’ouest du lac sont généralement plus grands que ceux situés au sud-ouest du lac, là encore parce qu’ils sont plus homogènes, et que cette homogénéité peut nous renseigner sur le type de couverture terrestre que l’on y trouve. En dehors de la taille, les segments ont un grand nombre d’autres attributs qui peuvent ou non être utiles dans une classification. Chaque segment a un nombre spécifique de segments voisins, et chaque segment est également plus foncé ou plus clair ou quelque part au milieu par rapport à ses voisins. Voir cette page pour une liste des attributs que vous pouvez calculer pour les segments dans le module d’extraction de caractéristiques d’ENVI (qui n’est pas le module le plus complet, et de loin). La possibilité d’obtenir toutes ces informations sur les segments peut aider à les classer, et ces informations ne sont pas toutes disponibles pour les pixels (par exemple, tous les pixels ont exactement quatre pixels voisins, sauf s’ils sont situés sur un bord de l’image, donc le nombre de pixels voisins n’est pas utile pour classer un pixel).

Il existe différents types d’algorithmes de segmentation, et tous sont compliqués à calculer. Certains sont code ouvert (open source), tandis que d’autres sont propriétaires, de sorte que nous ne savons pas vraiment comment ils fonctionnent. Nous n’allons donc pas entrer dans le détail des spécificités des algorithmes de segmentation, mais ils ont quelques points communs que nous pouvons prendre en compte.

• Échelle : Tous les algorithmes de segmentation requièrent un « facteur d’échelle », que l’utilisateur définit pour déterminer la taille qu’il souhaite donner aux segments résultants. Le facteur d’échelle ne correspond pas nécessairement à un certain nombre de pixels ou à un certain nombre de segments, mais doit généralement être considéré comme un nombre relatif. Ce qu’il signifie réellement en matière de taille des segments résultants est généralement déterminé par un processus d’essai et d’erreur.
• Couleur vs forme : Tous les algorithmes de segmentation doivent faire des choix quant à l’endroit où tracer les limites de chaque segment. Comme il est généralement souhaitable d’avoir des segments qui ne sont pas trop bizarres, cela implique souvent un compromis entre l’ajout d’un pixel dans un segment existant si a) ce pixel rend la couleur du segment plus homogène, mais donne aussi une forme plus bizarre, ou b) si ce pixel rend la couleur du segment moins homogène, mais donne une forme plus compacte. Un ou plusieurs paramètres contrôlent généralement ce compromis, et comme pour le paramètre « échelle », trouver le meilleur réglage est une question d’essais et d’erreurs.

Dans un monde idéal, la segmentation de l’image devrait produire des segments qui correspondent chacun à un, et exactement un, objet du monde réel. Par exemple, si vous avez l’image d’une zone urbaine et que vous souhaitez cartographier tous les bâtiments, l’étape de segmentation de l’image devrait idéalement aboutir à un segment distinct pour chaque bâtiment. Dans la pratique, c’est généralement impossible, car l’algorithme de segmentation ne sait pas que vous cherchez des bâtiments… si vous cherchez à cartographier des carreaux, il serait inutile d’avoir des segments correspondant à un toit entier, comme ce serait le cas si vous cherchiez à cartographier des pâtés de maisons. « Mais je pourrais définir le facteur d’échelle en conséquence », direz-vous, et c’est vrai dans une certaine mesure. Mais tous les toits n’ont pas la même taille ! Si vous cartographiez des bâtiments dans une image qui contient à la fois votre propre maison et le Pentagone, il est peu probable que vous trouviez un facteur d’échelle qui vous donne exactement un segment couvrant chaque bâtiment… La solution à ce problème est généralement une intervention manuelle, dans laquelle les segments produits par la segmentation initiale sont modifiés selon des règles spécifiques. Par exemple, vous pouvez sélectionner un facteur d’échelle qui fonctionne pour votre maison et laisser le Pentagone divisé en 1000 segments, puis fusionner ultérieurement tous les segments voisins qui ont des couleurs très similaires. En supposant que le toit du Pentagone soit assez homogène, tous ces segments seraient fusionnés, et en supposant que votre propre maison soit entourée de quelque chose d’apparence différente, comme une rue, une cour ou une allée, votre propre toit ne serait pas fusionné avec ses segments voisins. Cette possibilité de modifier manuellement le processus pour obtenir les résultats souhaités est à la fois une grande force et une importante faiblesse de l’analyse d’images basée sur les objets. C’est une force parce qu’elle permet à un analyste d’images de produire des résultats extrêmement précis, mais une faiblesse parce qu’il faut beaucoup de temps, même aux analystes experts, pour faire cela pour chaque image. Un exemple d’une bonne segmentation est présenté dans la figure 61, qui illustre également l’influence des changements dans les paramètres de segmentation (comparez les images en bas à gauche et en bas à droite)

Il convient de noter ici que l’analyse d’images par objet a été initialement développée et largement utilisée dans le domaine de l’imagerie médicale, pour analyser des images de rayons X, des cellules vues au microscope, etc. Deux choses sont très différentes entre l’imagerie médicale et la télédétection : dans le domaine de l’imagerie médicale, la santé des personnes est très directement affectée par l’analyse de l’image, de sorte que le fait qu’il faille plus de temps pour obtenir un résultat précis est moins contraignant que dans le domaine de la télédétection, où les impacts humains d’une mauvaise analyse d’image sont très difficiles à évaluer (bien qu’ils puissent finalement être tout aussi importants). L’autre problème est que les images étudiées par les médecins sont créées dans des environnements hautement contrôlés, avec pratiquement aucun bruit de fond, la cible de l’image toujours au point, et peuvent être refaites si elles sont difficiles à analyser. En télédétection, si la brume, un mauvais éclairage, la fumée ou d’autres facteurs environnementaux se combinent pour créer une image bruyante, notre seule option est d’attendre le prochain passage du satellite au-dessus de la zone.

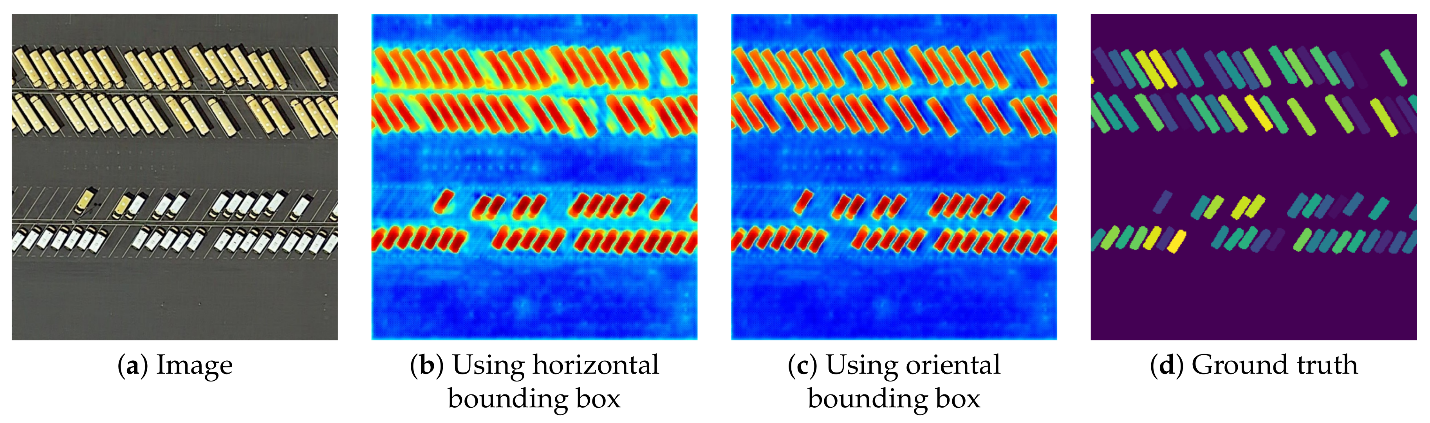
Figure 61: Exemple de segmentation d’image utilisée pour cartographier des véhicules individuels sur un parking à l’aide d’une imagerie aérienne. Une segmentation d’image est appliquée à l’image, et les segments qui correspondent aux caractéristiques d’un véhicule (forme, taille, couleur) sont ensuite identifiés. Efficient Hybrid Supervision for Instance Segmentation in Aerial Images (Figure 6) par Chen et al., CC BY 4.0.

Classification des segments

La classification des segments pourrait en théorie suivre les approches supervisées et non supervisées décrites dans le chapitre sur la classification par pixel. En d’autres termes, des zones dont la couverture terrestre est connue pourraient être utilisées pour calibrer un classificateur basé sur un ensemble prédéterminé d’attributs de segments (approche supervisée), ou un ensemble d’attributs prédéterminés pourrait être utilisé dans un algorithme de regroupement pour définir des groupes naturels de segments dans l’image, qui pourraient ensuite être étiquetés par l’analyste d’images (approche non supervisée). Cependant, dans la pratique, l’analyse d’images basée sur les objets se déroule souvent de manière plus interactive. Une approche courante consiste pour l’analyste à développer un ensemble de règles structuré sous forme d’arbre de décision, à voir le résultat produit par cet ensemble de règles, à le modifier ou à le compléter, puis à vérifier à nouveau, le tout dans un processus itératif très intensif pour l’utilisateur. C’est l’un des domaines où la télédétection ressemble plus à un art qu’à une science, parce que les analystes d’images acquièrent de l’expérience avec ce processus et deviennent de plus en plus compétents, développant essentiellement leur propre « style » de développement des ensembles de règles nécessaires pour obtenir une bonne classification. Par exemple, après avoir segmenté une image, vous pouvez vouloir séparer les surfaces artificielles (routes, trottoirs, stationnements, toits) des surfaces naturelles, ce qui est typiquement possible, car les premières ont tendance à être grises et les secondes non. Vous développez donc une variable qui quantifie le degré de gris d’un segment (par exemple en utilisant la valeur de « saturation » HSV, plus d’informations ici), et vous trouvez manuellement une valeur seuil qui sépare efficacement les surfaces naturelles des surfaces artificielles dans votre image. Si vous faites des études urbaines, vous voudrez peut-être aussi différencier les différents types de surfaces artificielles. Elles sont toutes grises, donc avec un classificateur basé sur les pixels, vous n’auriez pas de chance. Cependant, vous traitez des segments, et non des pixels, et vous quantifiez donc l’allongement de chaque segment, et définissez une valeur seuil qui vous permet de séparer les routes et les trottoirs des toits et des stationnements. Ensuite, vous utilisez la largeur des segments allongés pour différencier les routes des trottoirs, et enfin vous utilisez le fait que les stationnements ont des segments voisins qui sont des routes, alors que les toits n’en ont pas, pour les séparer. Trouver toutes les bonnes variables à utiliser (valeur de saturation HSV, allongement, largeur, classe de segments voisins) est un exercice intrinsèquement subjectif qui implique des essais et des erreurs et qui s’améliore avec l’expérience. Et une fois que vous avez créé une première structure d’arbre de décision (ou similaire) pour votre ensemble de règles, il est très probable que vos yeux soient attirés par un ou deux segments qui, malgré tous vos efforts, ont été mal classés (peut — être y a-t-il le toit occasionnel qui s’étend si loin au-dessus de la maison que son segment voisin est en fait une route, donc il a été mal classé comme un stationnement). Vous pouvez maintenant créer des règles encore plus sophistiquées pour remédier à ces problèmes spécifiques, dans un processus qui ne s’achève que lorsque votre classification est parfaite. C’est tentant si vous êtes fier de votre travail, mais cela prend du temps, et cela finit par aboutir à un ensemble de règles si spécifiques qu’elles ne fonctionnent jamais que pour l’image pour laquelle elles ont été créées. Une possibilité est de conserver l’ensemble de règles plus générique qui était imparfait, mais fonctionnait assez bien, puis de modifier manuellement la classification pour les segments que vous savez avoir été mal classés.

En résumé, la classification d’images basée sur les objets est une méthodologie relativement nouvelle qui repose sur deux étapes : 1) la division de l’image en segments contigus et homogènes, suivie par 2) une classification de ces segments. Elle peut être utilisée pour produire des classifications d’images qui surpassent presque toujours les classifications par pixel en termes en matière de précision, mais qui demandent beaucoup plus de temps à un analyste d’images. Le premier, le meilleur et le plus utilisé des logiciels d’OBIA dans le domaine de la télédétection sont eCognition, mais d’autres logiciels commerciaux comme ENVI et Geomatica ont également développé leurs propres modules d’OBIA. Les logiciels SIG tels que ArcGIS et QGIS fournissent des outils de segmentation d’images, ainsi que des outils qui peuvent être combinés pour effectuer la classification des segments, mais offrent généralement des flux de travail OBIA moins rationalisés. En outre, au moins un logiciel libre a été spécifiquement conçu pour l’OBIA, et des outils de segmentation d’images sont disponibles dans certaines bibliothèques de traitement d’images, comme OTB.