5 Visualisation et manipulation d’images satellites

La majeure partie de ce cours portera sur le type typique de « images satellites » que vous pouvez voir aux informations ou sur Google Earth, c’est-à-dire le type d’image produit par des capteurs optiques passifs. Ces images peuvent, à bien des égards, être considérées comme semblables aux photos que vous prenez avec votre téléphone, et vous pouvez donc faire des choses similaires pour les améliorer. Sauf que dans le contexte de la télédétection, « améliorer » ne signifie pas les retoucher pour supprimer les yeux rouges et créer des couleurs plus vives, mais les présenter de manière à mieux les interpréter à des fins déterminer. Il s’agit d’une forme de visualisation scientifique, un processus dans lequel l’affichage des données aide à les explorer et à les comprendre. Si l’exploration visuelle des données peut s’avérer plus utile que leur traitement par un algorithme informatique, c’est parce que les êtres humains sont exceptionnellement doués pour l’interprétation des modèles spatiaux. À titre d’exemple, imaginez que vous vous promenez dans un champ de l’est du Canada et que vous voyez la scène ci-dessous. Vous êtes immédiatement capable de réaliser que la partie sombre de l’image ne semble pas à sa place et qu’elle pourrait donc être importante, que la forme vous suggère qu’il s’agit d’un grand animal, et que vous pouvez faire appel à toutes sortes de contextes (la période de l’année, l’environnement, le fait que les ours sont connus pour vivre dans la région) pour vous aider à interpréter ce qui se passe.

Figure 29: Les humains sont exceptionnellement doués pour reconnaître les structures dans les images et, bien que la vision par ordinateur soit en plein développement, le cerveau humain surpasse encore souvent l’intelligence artificielle dans ce domaine. A Bear In The Woods par Linda Tanner, Flickr, CC BY-NC-ND 2.0.

Affichage en niveaux de gris, non amélioré

Il se passe beaucoup de choses en coulisses lorsque vous affichez une image sur un écran d’ordinateur. Pour en examiner les détails, nous prendrons d’abord l’exemple le plus simple possible, une image en niveaux de gris 8 bits, mais n’oubliez pas que les mêmes principes s’appliquent à des données de nature différente. Une image en niveaux de gris de 8 bits (communément, mais à tort, appeler aussi image en noir et blanc) correspond à une seule couche de données bidimensionnelle dont les valeurs vont de 0 à 255. Numériquement, le fichier image (par exemple, un fichier JPG, PNG, tif ou autre) contient un ensemble de chiffres, ainsi que des informations sur les dimensions de l’image. Dans l’exemple ci-dessous, l’image contient 16 pixels disposés en 4 lignes et 4 colonnes, et une valeur comprise entre 0 et 255 est associée à chaque cellule. Il s’agit de la valeur du numéro numérique (DN). La plupart des écrans d’ordinateur sont capables d’afficher 256 intensités lumineuses différentes, et utilisent pour cela trois couleurs (rouge, vert et bleu), ce qui permet de produire 256 * 256 * 256 = 16,8 millions de couleurs. Imaginez qu’il y a trois petits « canons à lumière colorée » à l’intérieur de chaque pixel de l’écran d’ordinateur, qui déterminent la quantité de lumière à produire, de chaque couleur, dans chaque pixel. Lors de l’affichage d’images en niveaux de gris, l’intensité de la lumière produite en rouge, vert et bleu est la même, ce qui donne 256 nuances de gris. La plus sombre d’entre elles (0 intensité lumineuse en rouge, 0 en vert et 0 en bleu) produit une couleur noire à l’écran, et la plus claire (255 en rouge, 255 en vert et 255 en bleu) produit du blanc. L’exemple de la figure 30 est donc la visualisation la plus simple (à droite) des valeurs DN du fichier (à gauche).

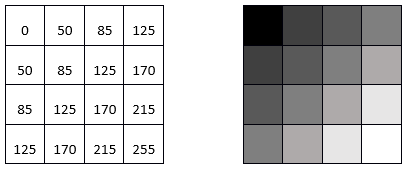
Figure 30: Image monocouche en niveaux de gris, montrant les chiffres numériques à gauche, et leur visualisation à droite. Par Anders Knudby, CC BY 4.0.

Affichage en couleurs vrai, non amélioré

La plupart des images ont plus d’une couche de données, et peuvent donc être utilisées pour produire des images en couleur. Les appareils photo des téléphones portables enregistrent des fichiers d’images comportant trois couches, correspondant au rouge, au vert et au bleu, de sorte que la visualisation de ces fichiers est facile grâce aux trois « canons à lumière colorée » de votre écran d’ordinateur. Il n’est donc pas surprenant qu’une visualisation en couleurs soit une visualisation dans laquelle vous affichez la couche de données « rouge » à l’aide du « canon » rouge, et ainsi de suite. Par exemple :

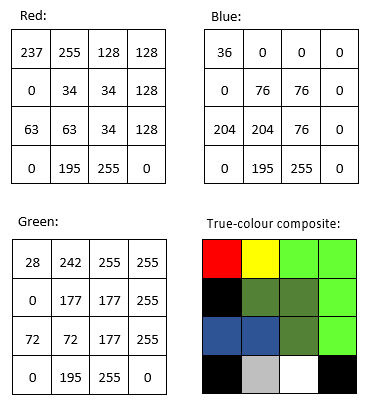
Figure 31: Les valeurs DN dans les bandes rouge, verte et bleue, et leur affichage direct dans un composite de couleurs vraies. Par Anders Knudby, CC BY 4.0.

Affichage en fausses couleurs, non amélioré

La plupart des capteurs optiques passifs des satellites enregistrent la lumière dans plus de trois « bandes » et produisent donc des fichiers d’images comportant plus de trois couches de données. Certaines de ces bandes peuvent être des nuances différentes de la lumière visible (par exemple, le violet), tandis que d’autres, comme l’infrarouge et l’ultraviolet, se situent en dehors du spectre visible par l’homme. Pour montrer de telles données, on utilise des visualisations en fausses couleurs. Le terme « fausses couleurs » indique simplement que ce qui est montré ne représente pas ce à quoi la zone de l’image ressemblerait pour un être humain, sans pour autant impliquer que l’image présente un défaut quelconque (en fait, les affichages en fausses couleurs sont très utiles). La visualisation en fausses couleurs est très variée — imaginez le nombre de combinaisons différentes de trois bandes que vous pouvez faire avec les données d’un capteur qui possède plus de 200 bandes… La visualisation en fausses couleurs la plus courante est souvent appelée « couleur-infrarouge », et elle affiche une bande « proche de l’infrarouge » à l’aide du canon rouge, une bande « rouge » à l’aide du canon vert, et une bande « verte » à l’aide du canon bleu. La figure 32 présente une comparaison côte à côte de l’affichage en couleurs vraies et en fausses couleurs d’une image Landsat contenant la ville de Zanzibar.

Figure 32: Affichages en couleurs vraies et en couleurs infrarouges d’une image Landsat contenant la ville de Zanzibar. Par Anders Knudby, CC BY 4.0.

Amélioration de l’image

Dans les exemples précédents, nous avons imaginé que les images contenaient toujours des valeurs comprises entre 0 et 255, fournissant ainsi les 256 différentes valeurs possibles que les canons à couleurs d’un écran d’ordinateur typique peuvent afficher. Il existe deux situations dans lesquelles l’utilisation directe de la valeur DN trouvée dans le fichier image pour déterminer l’intensité de la lumière produite par un pistolet à couleurs n’est pas la meilleure option :

• Tous les capteurs n’enregistrent pas les données sur 8 bits par pixel (par couleur). Pour les capteurs (anciens) qui utilisent moins de 8 bits, ou les capteurs (plus récents) qui utilisent plus de 8 bits, une conversion entre la valeur DN et l’intensité avec laquelle elle doit être affichée est généralement nécessaire.
• Si le capteur a produit une image sur une zone particulièrement claire ou sombre, ou du moins si une telle zone présente un intérêt spécifique, les valeurs trouvées sur cette zone (par exemple entre 50 et 80) peuvent être affichées en utilisant une gamme d’intensités plus large sur l’écran (par exemple entre 20 et 110), améliorant ainsi le contraste visuel sur la zone d’intérêt.

Pour mieux comprendre ces questions, nous devons examiner comment les valeurs DN sont stockées dans la mémoire de l’ordinateur. Nous allons considérer un seul pixel et sa valeur DN pour une seule bande. Pour un capteur 8 bits, cette valeur DN est stockée sur 8 bits, chacun d’entre eux pouvant être ON (1) ou OFF (0). La valeur est codée comme illustré à la Figure 33. Dans cet exemple, les bits représentant les valeurs 128, 32, 16, 8 et 2 sont tous activés, tandis que les autres sont désactivés. La valeur DN du pixel est donc calculée comme suit : 128 + 32 + 16 + 8 + 2 = 186. La gamme des valeurs possibles avec 8 bits va de 0 (tous les bits sont OFF) à 255 (tous les bits sont ON), soit un total de 256 valeurs possibles. En fait, le nombre de valeurs possibles, étant donné le nombre de bits, est facilement calculé comme 2n, où n est le nombre de bits.

Figure 33: Cet exemple illustre un pixel de 8 bits avec la valeur 186. Par Anders Knudby, CC BY 4.0.

C’est la raison pour laquelle les capteurs qui utilisent moins de 8 bits pour stocker le DN de chaque pixel ne peuvent pas produire 256 valeurs différentes. Toutefois, à titre d’exemple, si nous devions afficher directement les valeurs DN de 4 bits (valeurs DN comprises entre 0 et 15) sans changement, nous ne verrions que des nuances de gris très sombres (aucun capteur actuel n’enregistre d’informations en utilisant seulement 4 bits, mais les premiers capteurs Landsat n’utilisaient que 6 bits, et le problème est le même).

D’autre part, les capteurs qui utilisent 12 bits pour stocker chaque valeur DN (comme le font de nombreux capteurs modernes), contiennent des valeurs allant de 0 à 2¹²-1 = 4095. Pour afficher cette gamme de valeurs, nous devons les transformer pour qu’elles soient toutes comprises entre 0 et 255, ce qui est plus facile à faire en divisant simplement par 16 et en arrondissant vers le bas. Notez que dans ce cas, bien que l’écran de l’ordinateur ne soit pas capable d’afficher les données dans tous leurs détails, les algorithmes de traitement d’images pourront tout de même les utiliser.

Les choses deviennent plus intéressantes lorsque nous avons une image dans laquelle une gamme spécifique de valeurs est la plus intéressante. Un exemple courant est le type d’image de la figure 32, qui contient de l’eau (très sombre), de la terre (relativement sombre et largement verte) et des nuages (très clairs). À moins que nous ne soyons spécifiquement concernés par l’étude des nuages dans cette image, nous n’avons pas vraiment besoin de pouvoir distinguer les pixels dont les valeurs DN sont 245, 250 ou 255. Ce que nous pouvons faire, alors, c’est afficher tous les pixels « brillants » dont nous ne nous soucions pas vraiment avec la même couleur (blanc), et ainsi « réserver » plus de luminosités différentes avec lesquelles nous pouvons afficher les pixels pour les valeurs DN qui nous intéressent plus. Mathématiquement, cela signifie créer un tableau qui traduit chaque valeur DN, pour chaque bande, en une valeur de luminosité équivalente avec laquelle elle va être affichée à l’écran. Sur le plan graphique, nous pouvons représenter cela comme le fait la figure 34 ci-dessous, où les valeurs DN sont représentées sur l’axe des x, et la luminosité avec laquelle elles sont affichées est représentée sur l’axe des y. La ligne bleue représente l’utilisation directe de la valeur DN, sans amélioration du contraste. La ligne orange représente une amélioration linéaire du contraste, dans laquelle toutes les valeurs DN inférieures à 50 sont affichées avec une luminosité de 0, et toutes les valeurs DN supérieures à 240 sont affichées avec une luminosité de 255. Cela nous permet d’utiliser les 254 valeurs de luminosité restantes pour mieux afficher les petites différences entre les pixels dont les valeurs DN sont comprises entre 50 et 240. La ligne grise est une transformation de racine carrée qui conserve un certain contraste sur toute la gamme des valeurs DN, mais qui se concentre sur l’affichage des différences entre les pixels ayant des valeurs DN faibles, au détriment de ceux ayant des valeurs DN élevées. Les figures 35 à 37 présentent des exemples de ce que peut donner cette amélioration du contraste dans la pratique :

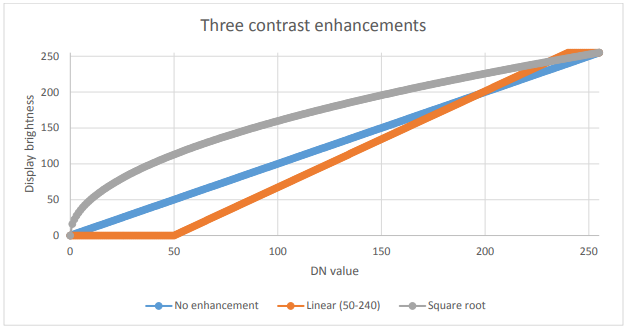
Figure 34: Trois options pour l’affichage des données 8 bits. Par Anders Knudby, CC BY 4.0.

Figure 35: Pas d’amélioration du contraste. Par Anders Knudby, CC BY 4.0.

Figure 36: Renforcement linéaire du contraste en utilisant les valeurs minimales et maximales de l’image à la place de 50 et 240 dans l’exemple ci-dessus. Par Anders Knudby, CC BY 4.0.

Figure 37: Amélioration du contraste, connue sous le nom d’égalisation d’histogramme. Cette technique est mathématiquement plus complexe que les exemples présentés ci-dessus, mais donne souvent de bons résultats. Par Anders Knudby, CC BY 4.0.

« Pan-sharpening »

Lorsque vous regardez des films hollywoodiens et que l’analyste de la CIA ou le policier étonnamment beau clique sur un bouton pour « améliorer » les images d’une caméra de surveillance, révélant ainsi les traits du visage de ce qui n’était auparavant qu’une tache floue, eh bien, c’est Hollywood. Le problème avec les images, c’est qu’elles ne sont que des données et qu’il est impossible de faire apparaître des détails (de nouvelles données) là où il n’y en a pas dans les données d’origines. Vous trouverez une explication amusante de cette idée générale ici. Cependant, avec certaines images satellites, il existe un type d’amélioration qui fonctionne (bien qu’il provoque des dégâts subtils sur la radiométrie de l’image). La technique en question est appelée « pan-sharpening », ce qui fait référence au fait que la plupart des capteurs optiques passifs des satellites ont une bande « pan- chromatique » qui enregistre des données sur la luminosité dans toutes les bandes visibles et à une résolution spatiale plus élevée que les bandes de couleur individuelles. Par exemple, les capteurs des satellites Landsat 4-7 ont des bandes bleues, vertes et rouges, tous avec une résolution spatiale de 30 mètres, et une bande pan- chromatique qui enregistre la lumière bleue et verte ainsi que la lumière rouge, avec une résolution spatiale de 15 mètres. Pour les capteurs modernes à haute résolution, la différence de résolution spatiale est encore plus grande, WorldView-2 ayant des bandes de couleur à une résolution de 2 mètres et une bande panchromatique à une résolution de 50 cm. En gros, nous pouvons donc combiner les informations de couleur des bandes de couleur individuelles avec les détails spatiaux de la bande panchromatique, pour obtenir quelque chose comme ce que vous voyez à la figure 38.

Plusieurs algorithmes peuvent être utilisés pour effectuer cette opération, et chacun d’eux utilise un ensemble différent d’hypothèses et de règles pour générer des informations de couleur pour chacun des pixels de l’image panchromatique. Bien que le contexte détermine quel algorithme est supérieur pour une image donnée, les résultats de la plupart des algorithmes sont impressionnants et peuvent grandement aider à l’interprétation visuelle des images satellites. La plupart des logiciels commerciaux de traitement d’images disposent d’un ou plusieurs algorithmes de pansharpening. Ainsi, bien que le processus en lui-même soit assez complexe, son application à une image se fait en un clic.

Figure 38: Illustration du pan-sharpening avec une image QuickBird. L’image en couleurs (à gauche, résolution de 2,4 m) est combinée avec l’image pan-chromatique (au centre, résolution de 60 cm) pour produire l’image pan-sharpened (à droite). Two-Path Network with Feedback Connections for Pan-Sharpening in Remote Sensing (Figure 7) par Fu et al, CC BY 4.0.

Rapports de bande et autres mathématiques de bande

Les sections précédentes ont principalement traité des différentes manières d’afficher les valeurs DN trouvées dans chaque bande — en niveaux de gris ou en couleur, directement ou transformées par l’amélioration du contraste, avec ou sans pansharpening. Une autre solution consiste à créer de nouvelles bandes à l’aide d’un processus communément appelé « Band Math ».

Par exemple, on peut vouloir produire une bande qui quantifie le degré de » rouge » d’un objet. Le problème de la bande » rouge » originale d’une image satellite typique est visible en comparant les valeurs DN » rouges » de la partie supérieure gauche de la figure 31 avec les couleurs indiquées dans la partie inférieure droite de la même figure. On peut dire que le pixel qui se trouve dans le coin supérieur gauche est ce que la plupart des gens considèrent comme » rouge « mais les deux pixels ayant les valeurs DN les plus élevées dans la bande » rouge » sont les pixels jaune et blanc (tous deux ont des valeurs DN » rouges » de 255). Malgré leur valeur DN « rouge » élevée, ces pixels n’apparaissent pas « rouges », car ils ont également des valeurs DN élevées dans une ou plusieurs autres couleurs. Pour mieux quantifier l’apparence « rouge » de chaque pixel, nous pouvons calculer ce que l’on appelle la « coordonnée chromatique rouge » (CCR). Pour chaque pixel, cette coordonnée est calculée comme suit : RCC = Rouge/(Rouge + Vert + Bleu), où Rouge, Vert et Bleu représentent les valeurs DN respectives de chaque pixel. Comme vous pouvez le voir dans les calculs de la figure 39, le pixel rouge dans le coin supérieur gauche a une valeur RCC plus élevée que tous les autres pixels, suivi par le pixel jaune à côté (parce que le jaune est « proche » du rouge). Notez que les mathématiques de bande opèrent sur chaque pixel individuellement, et effectuent la même opération mathématique sur tous les pixels d’une image. Ce faisant, elle produit une nouvelle bande qui est une fonction des bandes d’origine. D’autres utilisations courantes de la mathématique des bandes consistent à calculer des « rapports de bande », comme l’indice de végétation appelé « rapport simple », calculé comme suit : SR = NIR/Rouge, où NIR est une valeur (idéalement la réflectance TOA) dans la bande du proche infrarouge, et Rouge est la même valeur dans la bande rouge. Étant donné que les plantes saines réfléchissent très efficacement la lumière proche infrarouge, alors qu’elles absorbent la majorité de la lumière rouge (et reflètent donc très peu de lumière rouge à détecter par le capteur), les zones avec végétation ont tendance à avoir des valeurs de réflectance et de DN élevées dans la bande proche infrarouge et des valeurs faibles dans la bande rouge. Les zones avec végétation ont donc des valeurs de rapport simple très élevées, et ce rapport de bande peut donc être utilisé pour produire rapidement et facilement une visualisation qui aide les gens à distinguer les zones avec et sans végétation. Un indice de végétation encore plus populaire est l’indice de végétation par différence normalisée (NDVI), qui est calculé comme suit : NDVI = (NIR – Rouge)/(NIR + Rouge)

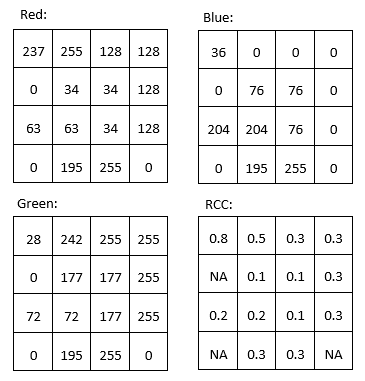
Figure 39: Les valeurs de rouge, vert et bleu sont les mêmes que dans la figure 31. La coordonnée chromatique rouge (CCR) est calculée comme suit : CCR = Rouge / (Rouge + Vert + Bleu). Les pixels ayant des valeurs DN de 0 dans toutes les bandes (c’est-à-dire les pixels noirs) ont reçu des valeurs NoData (NA). Par Anders Knudby, CC BY 4.0.

Les mathématiques des bandes peuvent être utilisées pour calculer de nouvelles bandes avec n’importe quelle combinaison de bandes d’entrées à laquelle vous pouvez penser.  Différents types de mathématiques des bandes sont utilisées, parmi de nombreuses autres applications, pour surveiller la déforestation mondiale, suivre les changements saisonniers de la couverture neigeuse, cartographier la profondeur des eaux et surveiller l’expansion urbaine.

« Tasseled cap transformation (TCT) »

Une application particulière de la mathématique des bandes, appelée « tasseled cap transformation », a été développée pour les données Landsat et est maintenant couramment utilisée pour produire un ensemble de bandes normalisé et facilement interprétable à partir des données d’origine. Elle a été développée à l’origine pour un instrument appelé Landsat MSS (qui ne fonctionne plus), et a depuis été mise à jour pour Landsat TM (les capteurs de Landsat 4 et 5), ETM+ (le capteur de Landsat 7), et OLI (le capteur optique passif de Landsat 8). L’idée qui sous-tend la transformation de la calotte est de produire trois nouvelles bandes, « verdure », « luminosité » et « humidité », qui décrivent les variations réelles de ces paramètres sur l’image. Dans une image satellite typique d’un paysage rural, les zones recouvertes de sols de couleur variable formeront une » ligne de sols » dans l’espace bidimensionnel (NIR/ROUGE), tandis que les zones de végétation se trouveront à l’écart de la ligne et les différents stades de croissance des plantes formeront ensemble une forme ressemblant grossièrement à un chapeau à tasse (figure 40). Les trois nouvelles bandes sont créées par une rotation effective des axes du système de coordonnées, de sorte que la « luminosité » est déterminée le long de la « ligne des sols » de la figure 40, la « verdure » est déterminée le long d’un axe qui s’éloigne de la ligne des sols et dont la valeur augmente à mesure qu’il se déplace vers le sommet du « chapeau à glands », et l’ » humidité » est déterminée le long d’un troisième axe (non représenté sur la figure 40) perpendiculaire aux deux premiers. Un exemple des résultats, basé sur une image IKONOS de l’Idaho, aux États-Unis, est présenté à la figure 41. Concrètement, chaque composante du chapeau à glands est calculée comme une somme pondérée des valeurs des bandes d’origine. Par exemple, pour les données Landsat TM, la » luminosité » est calculée comme suit : BR = 0,303 7 * BLEU + 0,2793 * VERT + 0,434 3 * ROUGE + 0,558 5 * NIR + 0,5082 * SWIR1 + 0,186 3 * SWIR2 (SWIR1 et SWIR2 sont deux bandes infrarouges à ondes courtes également présentes sur les capteurs Landsat TM).

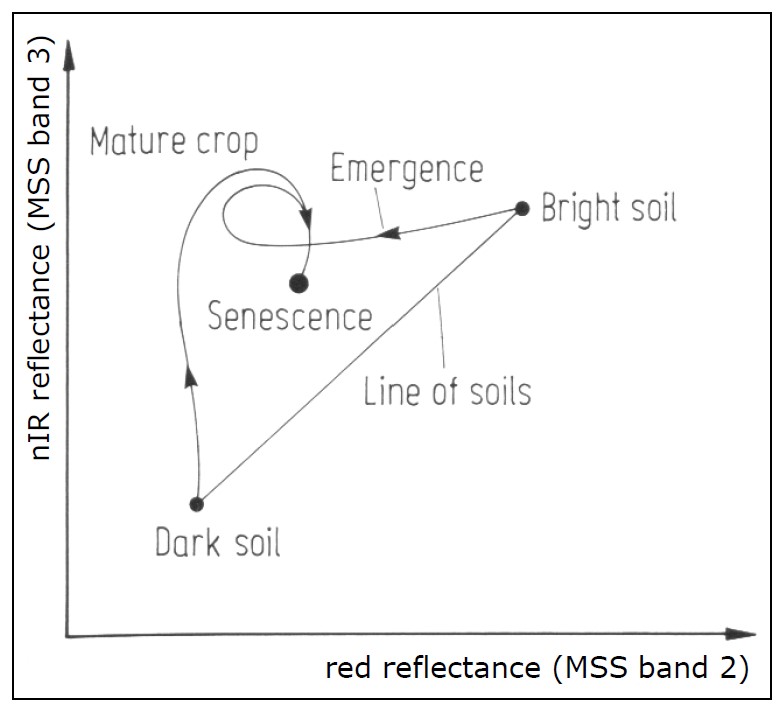
Figure 40: Le principe de la « tasseled cap transformation ». Des sols nus de luminosité variable tombent le long d’une ligne lorsque leurs valeurs sont tracées dans les bandes ROUGE et NIR, tandis que la végétation de densité croissante se trouve à l’intérieur du « chapeau », en haut et à gauche de la ligne des sols. La végétation à différents stades de croissance, poussant sur des sols de luminosité différente, forme ainsi une forme qui ressemble à un chapeau à glands. La formulation originale du transformation incluait une troisième dimension, en utilisant la bande verte. Tasseled Cap Transformation for bright and dark soil par Gurkengräber (adapted from Richards and Jia), Wikimedia Commons, CC BY-SA 4.0.

Figure 41: Un exemple de la « tasseled cap transformation » appliquée à une image IKONOS de l’Idaho, USA. tcap_example par Jason Karl, The Landscape Toolbox, CC0 1.0.

Analyse en composantes principales (ACP)

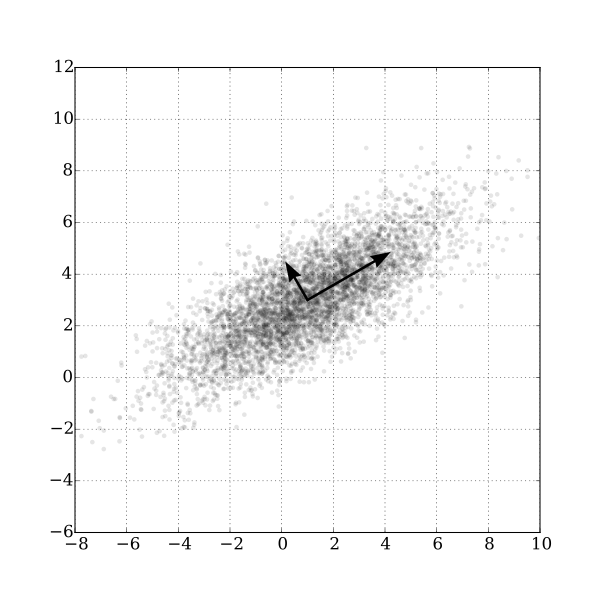
Figure 42: Un exemple bidimensionnel d’analyse en composantes principales. GaussianScatterPCA par Nicoguaro, Wikimedia Commons, CC BY 4.0.

Le dernier type de mathématique des bandes que nous allons examiner dans ce chapitre est semblable à la « tasseled cap transformation » dans la mesure où le calcul implique une somme pondérée des bandes originales, mais il est différent dans le sens où les pondérations sont déterminées à partir des propriétés de l’image elle — même, et en tant que telles, elles varient d’une image à l’autre. La figure 42 illustre bien le fonctionnement de cette méthode. Nous pouvons imaginer que chaque point du nuage de points est un pixel de notre image, et qu’il est représenté en fonction de sa valeur dans une bande sur l’axe des x et une autre bande sur l’axe des y. Il est clair, d’après la distribution des points, qu’il s’agit d’un pixel de l’image. Il ressort clairement de la distribution des points de la figure 42 que les points ayant des valeurs élevées dans une bande ont tendance à avoir également des valeurs élevées dans l’autre bande, et que la majorité de la distribution des points suit une ligne imaginaire allant du bas à gauche au haut à droite du graphique. L’orientation de cette ligne imaginaire est appelée la première composante principale (PC₁) et est illustrée par la flèche la plus longue. Mais il existe également une variation orthogonale (perpendiculaire) à la PC₁. C’est l’orientation de la deuxième composante principale, PC₂, illustrée par la flèche la plus courte. Selon le nombre de bandes dans une image, on pourrait continuer à trouver de nouvelles lignes de ce type dans les troisièmes, quatrièmes, etc. dimensions, chacune étant orientée selon la plus grande distribution de points dans toute orientation perpendiculaire à toutes les composantes principales précédentes. Dans la figure 42, l’ensemble de données original n’avait que deux dimensions, et deux composantes principales ont donc été créées. La longueur de chaque flèche correspond à la quantité de distribution totale capturée par chaque composante principale, et il est clair que la PC₂ a capturé assez peu de la distribution des points originaux. Cela peut être interprété comme le fait que la PC₂ contient très peu d’informations, et souvent les composantes principales de rang supérieur peuvent être entièrement supprimées avec une faible perte d’informations. Avec cette connaissance, de nouvelles bandes peuvent être créées, dans lesquelles la valeur de chaque pixel n’est plus sa valeur DN dans les bandes originales, mais plutôt sa valeur le long de chacun des axes des composantes principales. C’est là le principal atout de l’ACP : elle permet de transformer les données en un plus petit nombre de bandes (occupant ainsi moins d’espace sur le disque dur, et permettant une lecture et un traitement plus rapides) sans perdre beaucoup d’informations. Des recherches ont même montré que pour certains types d’images (par exemple, une image Landsat sans nuages d’une zone agricole), des composantes principales spécifiques tendent à correspondre à des variables environnementales spécifiques, telles que l’humidité du sol, la couverture végétale, etc. Cependant, une mise en garde s’impose ici. Comme l’orientation des composantes principales (les flèches de la figure 42) dépend de la distribution de la totalité des valeurs des pixels dans chaque image individuelle, les valeurs des composantes principales d’un pixel ne sont pas directement interprétables et peuvent varier considérablement entre les images, même pour des pixels identiques. L’ACP peut donc vous aider à réduire le volume de données d’une image, mais elle détruit (ou du moins, complique) l’interprétation dans le processus. Une autre très bonne explication de l’ACP, y compris un nuage de points animé qui, selon moi, explique très bien les choses, se trouve ici.